如何確定外接球球心的位置

朱賢良

(安徽省樅陽縣宏實中學 246700)

直觀想象是數學核心素養的六大方面之一，強調借助幾何直觀和空間想象感知事物的形態與變化，利用空間形式特別是圖形來理解和解決數學問題．在高中數學學習過程中，直觀想象素養的培育與考查常通過三視圖、空間平行與垂直、空間角與距離等問題的形式展開．隨著全國高考命題的統一，有關空間幾何體的外接球問題日益受到重視，成為考查直觀想象素養的又一熱門題型．

求解外接球問題的關鍵在于確定球心的位置，而確定球心位置的依據不外乎球心的兩個特性：一是球心到球面上各點的距離都等于半徑，二是球心與截面圓圓心的連線垂直于截面(球的截面圓性質)．由此出發，或利用一些特殊模型，或借助一般方法，即可讓外接球球心畢露．

一、長方體的外接球

例1-1 (2017年高考全國Ⅱ卷·文15)長方體的長、寬、高分別為3、2、1，其頂點都在球O的球面上，則球O的表面積為____．

點評長方體是重要的立體幾何模型，在認識空間結構特征、培養直觀想象素養中發揮著基礎的作用．在解決空間幾何體的外接球問題時，要充分借助長方體模型的幾何特征，簡化求解過程．

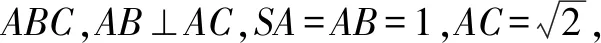
點評當三棱錐某一頂點處的三條棱兩兩垂直時，可將此三棱錐視為長方體的一角，進而借助長方體的外接球來實現求解．

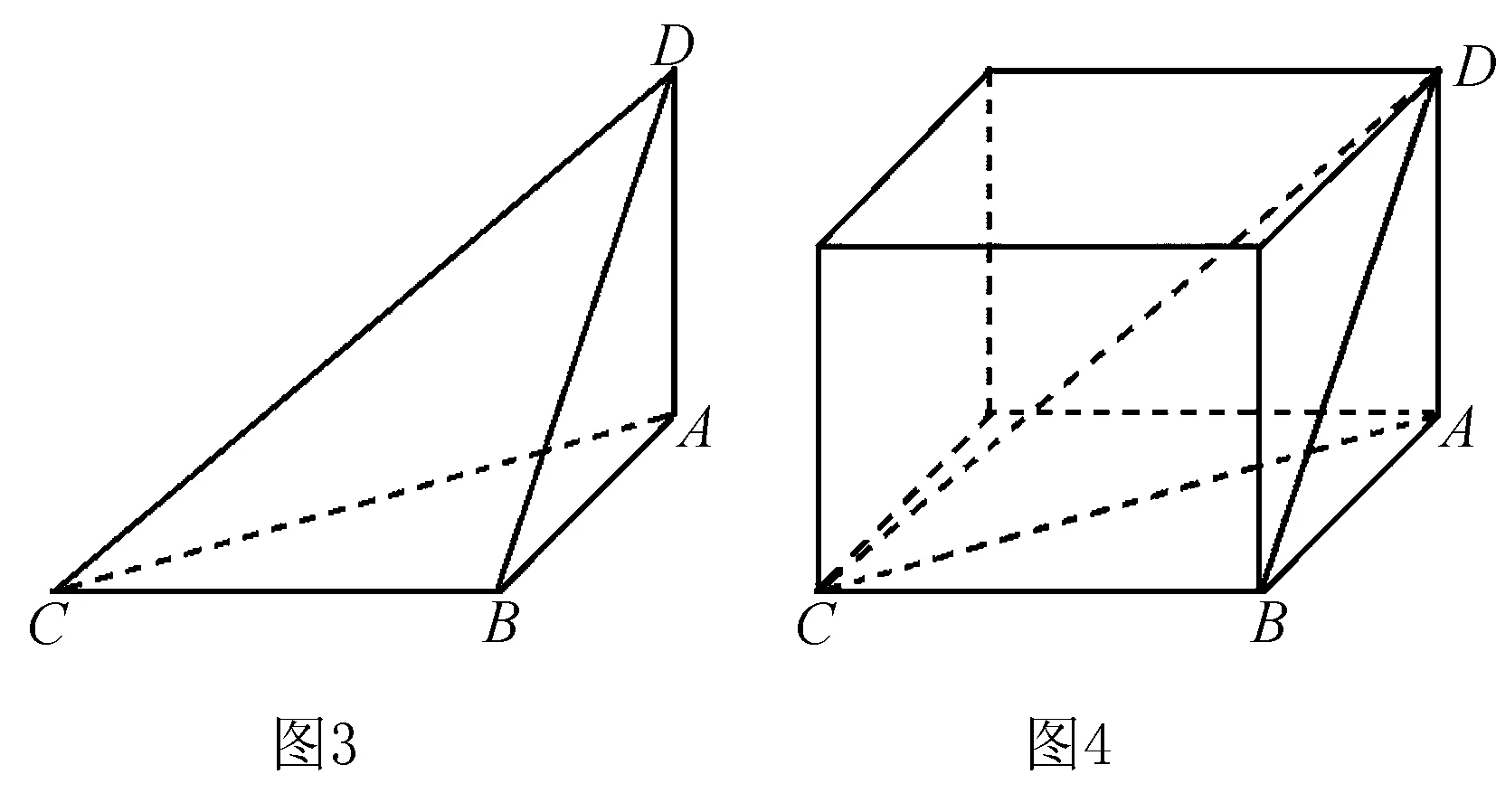
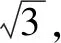
點評本題中，三棱錐D-ABC的底面△ABC為直角三角形，過銳角頂點A的側棱與底面垂直，具備此幾何特征的三棱錐(四個面均為直角三角形)即可補形成長方體．若過底面三角形的直角頂點B的側棱垂直于底面，則此模型即為例1-2中的三棱錐．

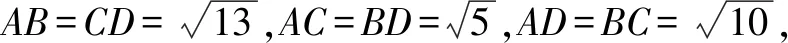
簡解因為四面體ABCD的三對對棱長對應相等，可將其分別視為長方體三對面的對角線，從而將四面體補形成長方體，如圖5所示．

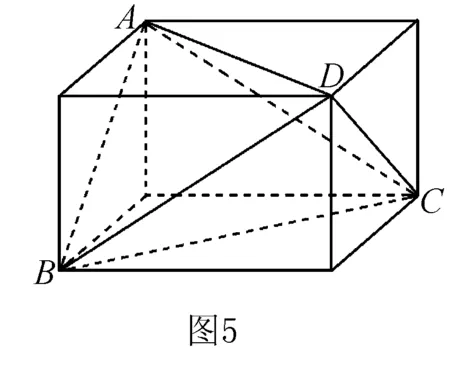
點評當三棱錐的三對對棱長對應相等時，此三棱錐也可以補形成長方體，三棱錐的三對對棱長即為長方體六個面的對角線之長．這種補形構造的思路較為隱蔽，解題時要注意判斷與識別．又比如正四面體，可以通過這種思路將其補形成正方體．

例1-5(2013年高考遼寧卷·理10文10)已知直三棱柱ABC-A1B1C1的6個頂點都在球O的球面上．若AB=3，AC=4，AB⊥AC，AA1=12，則球O的半徑為( ).

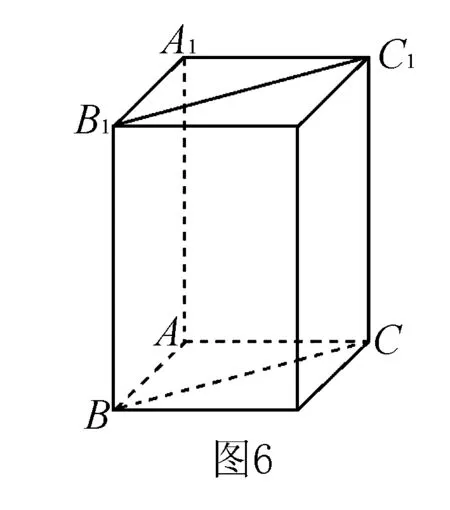
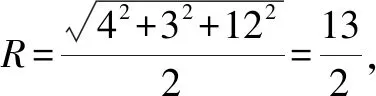
點評當直三棱柱的底面恰為直角三角形時，兩個這樣完全相同的三棱柱可拼接成一個長方體．需要注意的是，這里必須具備底面為直角三角形、側棱與底面垂直這兩個幾何特征．

二、由共斜邊的兩個直角三角形所圍成的三棱錐的外接球

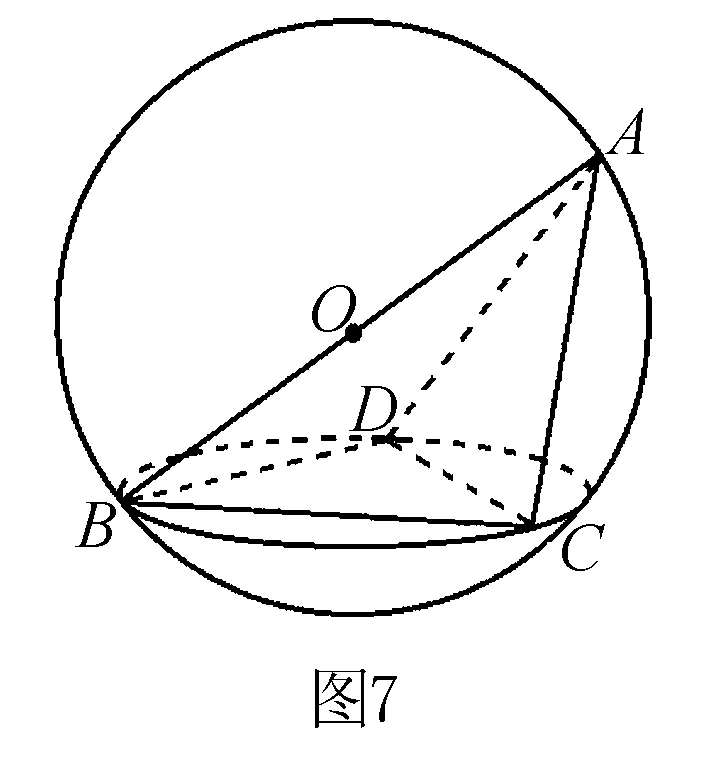
外接球的球心到球面上每一點的距離均為半徑R，可以根據外接球球心的這一特征來確定球心的位置．比如，若四面體ABCD是由共斜邊的兩個直角三角形所圍成的，如圖7所示，△ABC與△ABD均為直角三角形，AB為公共的斜邊，O為AB的中點，則根據直角三角形斜邊中線等于斜邊的一半可知，OC=OD=OA=OB，即點O到四點A,B,C,D的距離相等，故點O就是四面體ABCD外接球的球心，公共的斜邊AB就是外接球的一條直徑．

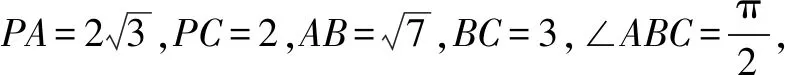
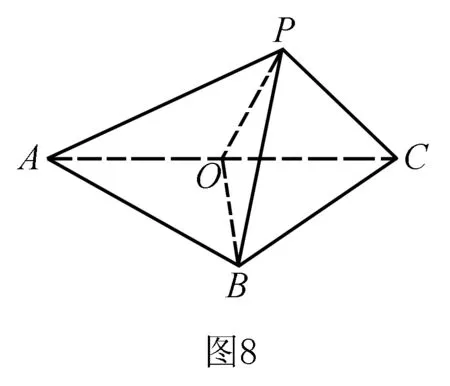
點評本題在求解過程中，需要從邊長關系出發來認識三棱錐模型，把握“共斜邊的兩個直角三角形”這一典型幾何特征．

A．2π B．4π C．6π D．8π

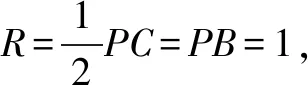
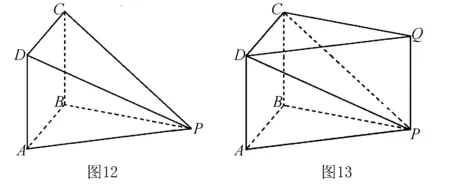
點評實際上，三棱錐P-BCO的四個側面皆為直角三角形，也可以將其補形成長方體后再確定外接球球心的位置，解法同例1-3．

三、直棱柱的外接球

例3-1(2009年高考全國Ⅰ卷·理15)直三棱柱ABC-A1B1C1的各頂點都在同一球面上．若AB=AC=AA1=2，∠BAC=120°，則此球的表面積等于____．

點評在計算底面外接圓的半徑時，要注意結合幾何圖形及正弦定理求取．

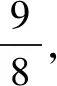
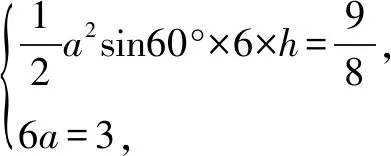
點評根據平面幾何特征，正六邊形外心即中心與各頂點的連線將正六邊形分割為六個全等的等邊三角形，由此求得正六邊形的面積及其外接圓的半徑．

例3-3 已知某幾何體的三視圖如圖11所示，則該幾何體的外接球的表面積為( ).

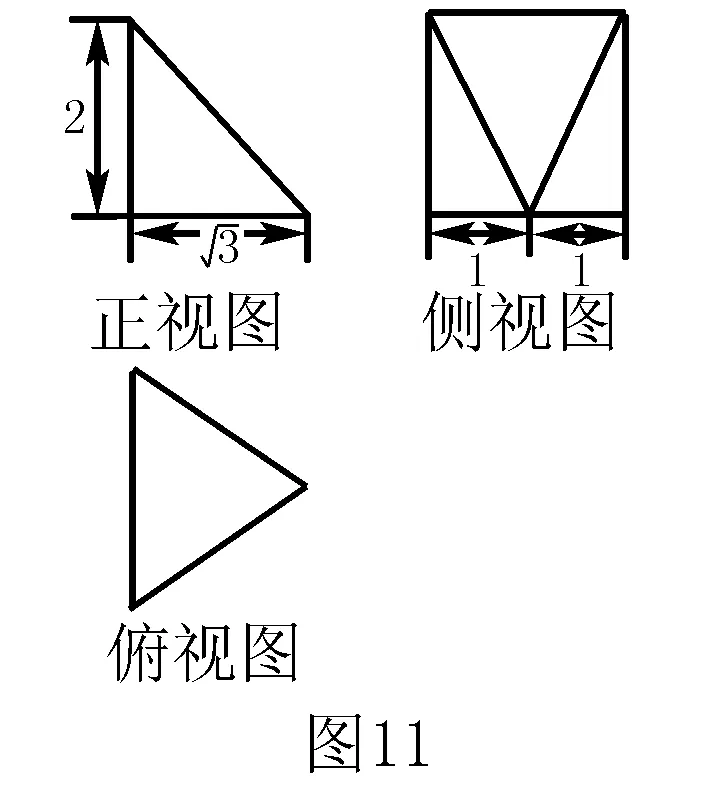
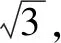
點評本題在求解時，要突破兩個難點：一是根據三視圖，準確還原幾何體的結構特征；二是根據幾何體的結構特征，靈活通過補形成直棱柱來確定外接球球心的位置及半徑大小．

四、確定外接球球心位置的一般途徑

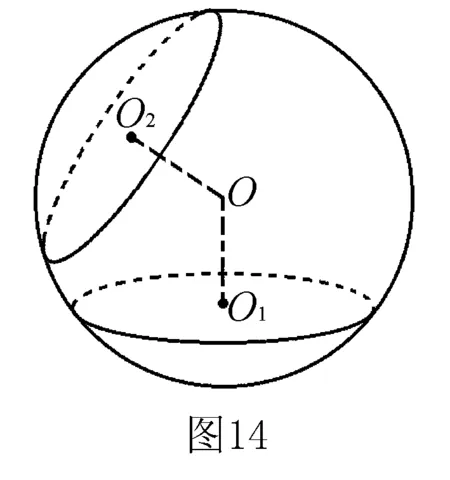
以上借助三類特殊多面體的結構特征來判定其外接球球心的位置，進而求解外接球的相關問題．除了要掌握上述特殊模型，還需要掌握確定外接球球心位置的一般方法．正是基于球心與截面圓圓心的連線垂直于截面，故多面體外接球球心必在過表面多面形的外心、且與表面垂直的直線上．如圖14所示，過兩截面圓的圓心且垂直于兩截面的直線的交點即為球心O．

例4-1 如圖15所示，在由邊長為1的小正方形組成的網格中畫出了某多面體的三視圖，則該多面體的外接球的表面積為( ).

A．27π B．30π C．32π D．34π

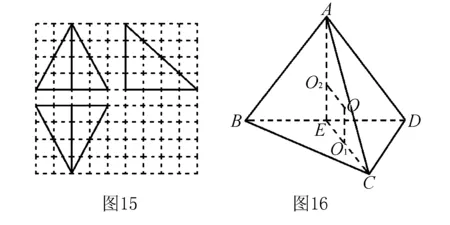
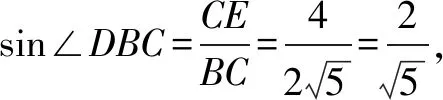
點評多面體外接球球心在過表面多面形的外心、且與表面垂直的直線上，而在選擇表面多邊形時要注意選擇特殊形狀的多邊形，如正三角形、直角三角形、等腰三角形等，以比較容易地確定外心位置并求出外接圓半徑大小．本題中，△BCD,△ABD為全等的等腰三角形，其所在平面又垂直，這有助于分析外心位置、確定線面的位置關系．

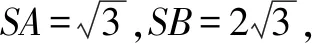
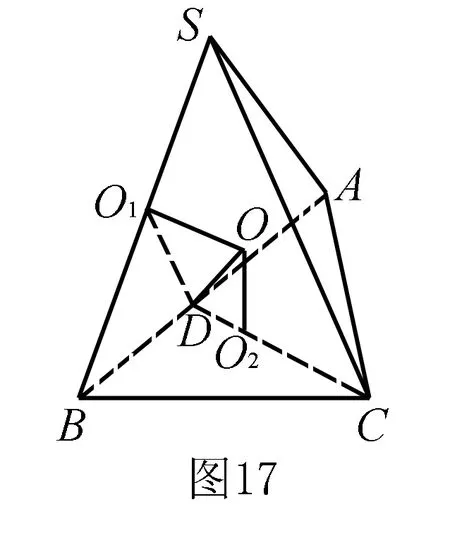
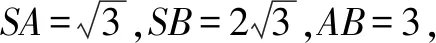
分別過O1,O2作平面SAB、平面ABC的垂線，則兩垂線的交點O即為三棱錐S-ABC外接球的球心．

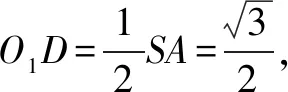
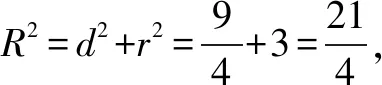
點評本題中，△SAB與△ABC分別為直角三角形、等邊三角形，借助這兩個特殊形狀的三角形外心來確定外接球球心的位置，從而將問題轉化為平面幾何問題，體現了轉化與化歸思想，實現復雜問題簡單化，從而使得問題迎刃而解．

通過立體幾何的教學，發展學生的直觀想象素養是數學教學的重要目標之一，它可以通俗地表示為“會想到、能解決”．比如本文在尋找幾何體的外接球球心的過程中，注重結合一些常見、特殊、簡單的幾何模型來提取空間幾何體的基本屬性和幾何特性，將問題求解程序化、規律化，降低問題解決的難度，達到“會想到、能解決”的效果．設計教學活動時，多引導學生對此類問題進行分類總結，進而把握幾何關系的本質和規律，這無疑非常有助于學生空間想象能力的提升．