分形結構稀疏孔徑陣列的成像性能*
郝未倩 梁忠誠 ? 劉肖堯 趙瑞 孔梅梅 關建飛 張月
1) (南京郵電大學電子與光學工程學院, 南京 210023)
2) (中國空間技術研究院北京空間機電研究所, 北京 100094)
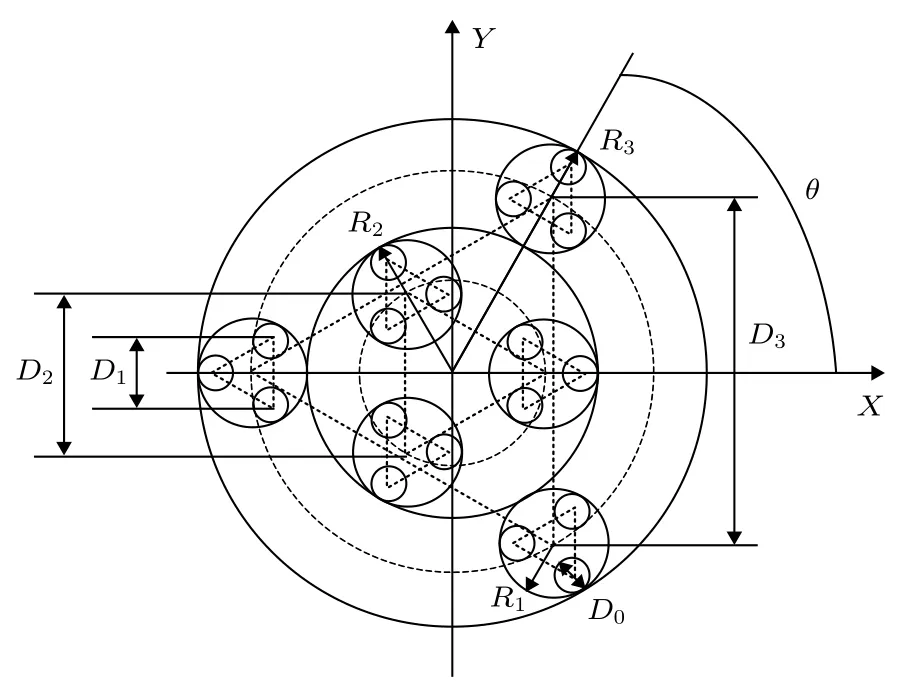
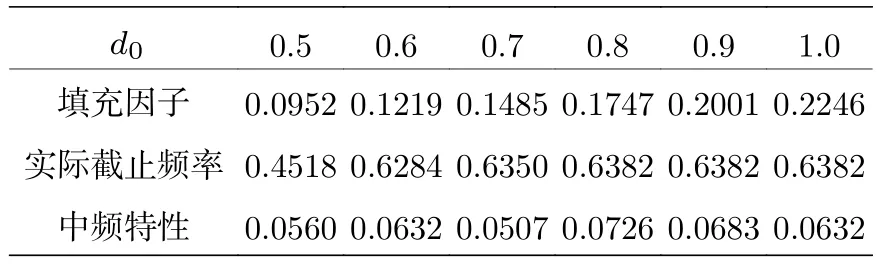
根據分形的自相似性理論提出一種分形稀疏孔徑陣列結構.該陣列是以Golay-3為分形結構單元, 按自相似方式擴展構成的一種多層分形陣列結構.采用無量綱約化參數對其結構進行表征, 給出光瞳函數和調制傳遞函數解析表達式.通過數值計算分形結構在不同填充因子和不同外層旋轉角下的調制傳遞函數、實際截止頻率和中頻特性, 比較分析了當孔徑數分別為 N= 3, N= 9, N= 18 陣列的 MTF 及特性參數.結果表明,當填充因子為 0.0952 空間遙感對于高分辨率圖像的要求不斷提高.對于單孔徑(主鏡)望遠鏡而言, 越高的空間分辨率需要越大的孔徑[1?3].光學系統的角分辨率d正比于工作波長l與入瞳口徑D之比[4], 增大光學系統的孔徑是提高空間分辨率的傳統方法.但是光學系統的重量、體積和制造檢測的難度, 也會隨著口徑的急劇增大而無法承受[4,5].于是綜合孔徑成像技術應運而生[6].綜合孔徑成像又稱稀疏孔徑成像, 它通過多個子孔徑光學系統的合理排布, 以達到增加系統孔徑、提高成像質量的目的.由于子鏡系統的體積和重量相對較小, 綜合系統的制造和檢測難度也相應降低[7,8].因為稀疏孔徑成像有較大的中頻損失, 所以子鏡陣列結構的優化設計和中頻補償是綜合孔徑成像系統的關鍵技術之一[9?11]. 1971年, Golay[12]最先提出一種稀疏孔徑結構, Golay結構因有較高緊密性和較小冗余度而被廣泛應用.1988年, Cornwell[13]對二維圓周陣列進行優化, 給出3—12個子孔徑在圓周上最優的無冗余布局.目前, 國際上在陣列結構優化和中頻補償方面已有廣泛的研究[14,15].國內對稀疏孔徑成像也有較多的研究.蘇州大學曾提出了一種復合三子鏡稀疏孔徑結構[16].北京工業大學提出一種建立在典型光學稀疏孔徑陣型基礎上的復合孔徑陣列結構[3,17].北京航天航空大學在均勻圓周陣列的基礎上提出一種多圓周陣列的稀疏孔徑結構[18,19].此外, 北京航天航空大學[20,21]、南京理工大學[22]、中國科學院西安精密研究所[10]和本課題組[23]都陸續對稀疏孔徑系統進行了優化和仿真成像分析[24]. 分形是具有自相似性、無標度性和自仿射性的一類結構[25].典型的分形如康托集、柯赫曲線和皮亞諾曲線.分形結構通常在不同尺度上有著某種自相似的性質, 也就是局部形態和整體形態的相似.根據分形結構的自相似和多尺度特點, 本文提出一種基于分形結構的稀疏孔徑陣列, 用于綜合孔徑成像系統, 并分析此陣列結構的性能指標. 本節給出一種基于Golay-3為單元的分形結構陣列的設計分案.Golay-3是一種最小的非冗余稀疏孔徑結構, 其子孔徑圓心位于正三角形頂點,正三角形邊長D是該結構的特征長度.特征長度的層層遞增可以構成自相似結構, 達到擴展陣列口徑的目的.設陣列結構的層數為n,D1,D2,D3,···,Dn分別為各層的特征長度, 其中D1稱為分形單元基線.從第二層開始, 各層正三角形中心均位于同一點.在各層三角形頂點處均放置一個分形單元依次層層嵌套, 向外拓展.分形陣列結構層數n與子孔徑總數N遞推關系為 在圖1 中,R1,R2,R3,···,Rn分別為各層外接圓半徑, 子孔徑直徑為D0, 各層外接圓半徑與特征長度的關系由(2)式給出. 圖1 分形陣列結構Fig.1.Fractal array configuration. 考慮各層方位的相對變化情況, 第n層相對于X軸的旋轉角稱為n層旋轉角θn.本文考慮n=3,θ1=0,θ2=0,θ3=θ的 情 況, 通 過 改 變D1,D2,D3的大小及第三層旋轉角θ3=θ, 分析其結構和性能特征.為了保證旋轉時各層子孔徑不重疊, 對特征長度做如下約束: 此時, 孔徑的光瞳結構如圖1所示, 光瞳函數可以表示為 其中circ()為圓函數, *表示卷積. 為了使得計算結果具有普適性, 現以D1為單位將特征長度無量綱化, 得到以下約化參數 n=3時, 獨立的特征長度有 4 個 (D0?D3) , 約化后的特征長度有3個 (d0,d2,d3).在(3)式的約束下, 獨立的特征長度僅剩下一個d0, 且取值范圍為0 該分形結構陣列的幾何特征包括填充因子和包圍圓半徑.填充因子F定義為稀疏孔徑通光面積(子孔徑通光面積之和)與包圍孔徑面積的比值.下式是n=3 時的填充因子表達式 由此可知, 填充因子的改變僅由子孔徑直徑d0決定.當d0=1 時, 填充因子達到最大值 圖2(a)是子孔徑直徑d0與填充因子F的關系圖.由圖可見, 隨著d0的增大, 填充因子F單調增大. 在(2)式約束條件下分形陣列結構的包圍圓半徑Rn與d0的關系為 圖2(b)是包圍圓半徑與層數n的關系.如果取消(2)式的限制, 系統口徑將隨著層數的增加而迅速增加. 設稀疏孔徑系統每一個子孔徑均為無遮攔圓形光瞳, 則任意結構的調制傳遞函數(modulation transfer function, MTF) 為[4] 式中 M TFd為與子孔徑相同大小的單孔徑非衍射受限系統的MTF, 表達式為 式中 (xj?xk,yj?yk) 表示子孔徑的相對位置.顯然, 稀疏孔徑的MTF由子調制傳遞函數分布在二維頻率域內的不同位置決定, 子孔徑中心點陣的二維相關點陣決定二維頻率點的位置.故可以調節子孔徑的相對位置, 使之達到實際使用時對傳遞函數的要求.填充因子F取22.46%時, 分形結構對應的MTF如圖3.從圖中可知, 與全孔徑系統相比,分形陣列結構的MTF的旁瓣增多, 中高頻區域有很大的衰減.其MTF總體上呈六角邊形分布, 在60°的整數倍方向取到最大截止頻率. 圖2 結構特征 (a)子孔徑直徑與填充因子曲線圖; (b)結構層數與包圍圓半徑關系Fig.2.Configuration characteristics:(a) Sub-aperture diameter and fill factor curve; (b) the relationship of the number of fractal configuration and the radius of aperture. 圖3 分形陣列 MTF(F= 22.46%) (a)三維 MTF; (b) MTF 俯視圖Fig.3.MTF of fractal array (F= 22.46%):(a) There-dimensional MTF; (b) top-view MTF. 采用無量綱方法將孔徑參數約化后, 子孔徑直徑d0的變化通過填充因子F(d0) 表現出來.一般的稀疏孔徑結構多采用較大的填充因子, 以實現沒有零點和提高中頻特性.圖4給出分形結構隨填充因子變化的MTF曲線, 圖4(a)為沿fx的歸一化截止空間頻率, 圖4(b)為沿fy的歸一化截止空間頻率.當d0=0.5 時, MTF 低頻部分有很大起伏, 且在 0.52 附近出現零點.當d0>0.5 時, MTF 曲線平緩且連續, 有較好的中頻特性, 是分形結構特點的反映.雖然分形結構填充因子的改變會導致MTF 曲線發生變化, 但在 0.5 實際截止頻率ρR為MTF第一次出現零值時所對應的空間頻率.在陣列設計時, 應盡可能地最大化ρR, 使其接近包圍圓所確定的截止頻率[4]. 中頻特性 M TFmidfreq定義為子孔徑截止頻率和包圍圓孔徑截止頻率范圍內MTF的平均值, 表征綜合孔徑系統在中高頻區域內的響應能力.高分辨成像系統要求具有很好的MTF中高頻特性.計算公式如下[11]: 由表1可見, 當填充因子為0.0952時其實際截止頻率較低, MTF 起伏較大, 中頻特性較差.隨著填充因子的增大, 系統實際截止頻率增大, 且在一定數值范圍內波動, 體現了分形陣列結構的自相似特征.填充因子的降低并沒有明顯改變MTF曲線波動和實際截止頻率, 在實際應用中, 可以選取較小的填充因子來降低制造難度. 表1 分形陣列在不同填充因子下的特性指標Table 1.Characteristics of fractal array with different fill factors. 圖4 分形結構隨填充因子變化MTF曲線 (a)沿fx歸一化頻率方向; (b)沿fy歸一化頻率方向Fig.4.MTF curves of fractal array with different fill factor:(a) Normalized frequency along fx - axis; (b) normalized frequency along fy - axis. 當θ1=0,θ2=0 時, 第三層旋轉角θ3=θ稱為外層旋轉.外層旋轉角度的變化會對MTF出現周期性影響, 變化周期為 π /3.取d0=1 的情況.圖5為分形孔徑陣列外環分別旋轉 0°, 15°, 30°和 45°時, 旋轉前后 MTF 沿fx和fy方向的截面圖.稀疏孔徑系統的MTF隨空間頻率的增大在中低頻部分下降比較快, 在中高頻比較平坦, 但有適當起伏;在fx和fy方向, 分形結構MTF在截止頻率內無零點, 且比較平緩.外層旋轉會導致系統的MTF沿不同方向的分布產生變化. 圖6給出實際截止頻率隨外層旋轉角的變化曲線.此時子孔徑直徑d0=1 , 填充因子為22.46%.可以看出, 隨著外環旋轉, 系統實際截止頻率雖有下降趨勢, 但總體沒有太大變化, 影響甚小.總之,外層旋轉對MTF和實際截止頻率的影響不是很大. 圖5 分形陣列隨外環旋轉角度變化 MTF 曲線 (a)沿fx歸一化頻率方向; (b)沿fy歸一化頻率方向Fig.5.MTF curves of fractal array with different outer layer rotational angles:(a) Normalized frequency along fx - axis; (b) normalized frequency along fy - axis. 圖6 實際截止頻率隨外層旋轉角的變化曲線Fig.6.The curve of the practical frequency with outer layer rotational angles. 為了進一步分析自相似結構效應, 對N= 3,N= 9,N= 18 時的陣列進行比較,N= 3,N=9時陣列結構如圖7所示.采用填充因子F=0.2246的情況, 三種陣列的MTF曲線如圖8所示.在歸一化頻率fx方向,N= 3時分形陣列結構在歸一化頻率為0.28處出現零值,N= 9時分形陣列結構在0.31處出現一個低谷.在整個頻率范圍內有較大波動, 隨頻率呈起伏式下降.N= 18 時結構MTF曲線平緩且截止頻率高, 在MTF截止頻率范圍內沒有零點.在歸一化頻率fy方向,N= 3,N= 9時結構的MTF曲線差別不大, 出現較多的頻率缺失.N= 18時結構的MTF有些起伏但在中高頻趨于平穩, 在0.64處趨于零值. 由實際截止頻率定義和(11)式計算分析可得3 種陣列的特性指數, 如表2 所示.N= 3,N=9時陣列結構實際截止空間頻率很低.綜合分析三種陣列結構的特性指數, 在F不變的條件下, 隨著分形陣列結構孔徑數的增加, 實際截止頻率和中頻特性數值都顯著增加.在相同的填充因子情況下,增加子孔徑數可以改善中高頻平穩性, 提高系統的實際截止頻率. 圖7 N= 3, N= 9 陣列結構Fig.7.N= 3, N= 9 array configuration. 圖8 3 種陣列的 MTF 曲線 (F= 22.46%) (a)沿 fx歸一化頻率方向; (b)沿 fy歸一化頻率方向Fig.8.MTF curves of three kinds of array configuration (F= 22.46%):(a) Normalized frequency along fx - axis; (b) normalized frequency along fy - axis. 表2 3 種陣列的特性指數Table 2.Characteristics of three kinds of array configuration. 本文利用分形自相似性, 研究了一種以Golay-3結構為單元的分形綜合孔徑陣列.給出子孔徑直徑d0與MTF曲線的關系, 計算了實際截止頻率和中頻特性.在 0.51 引 言
2 分形結構陣列
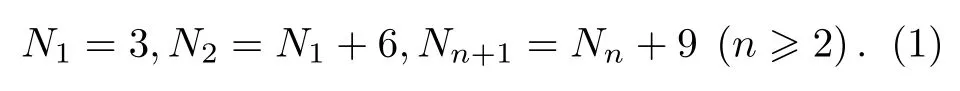
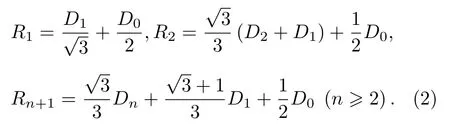
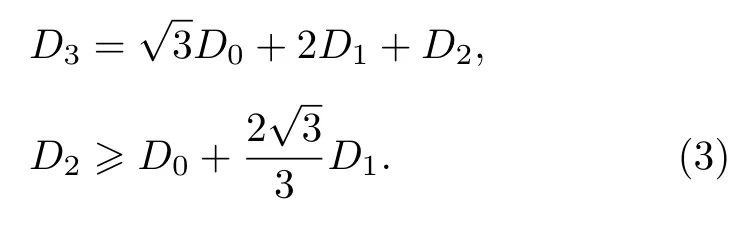
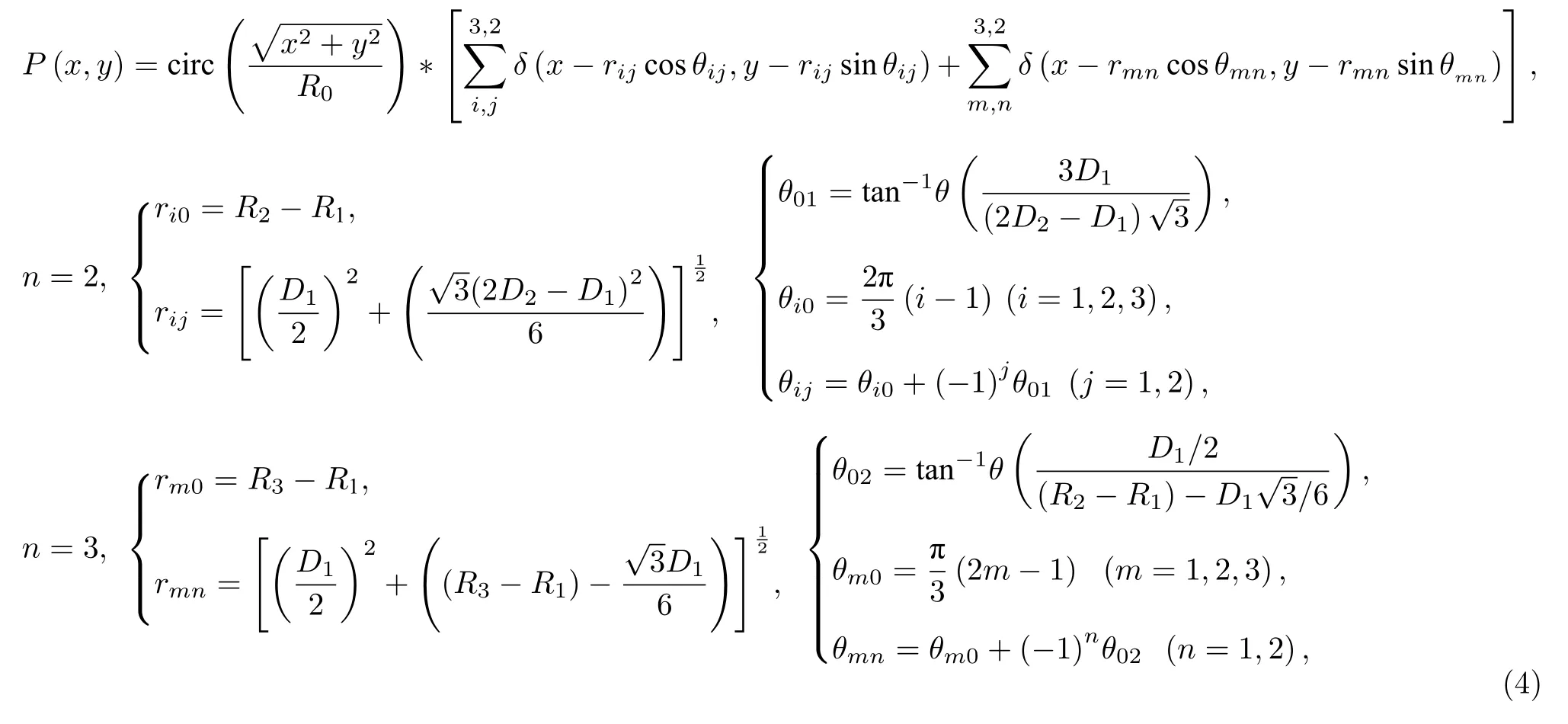
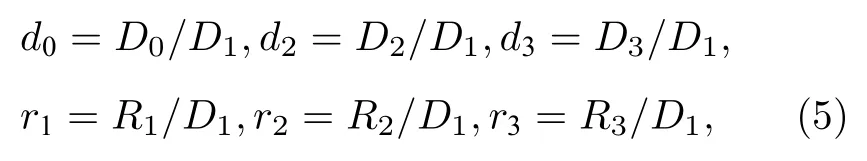

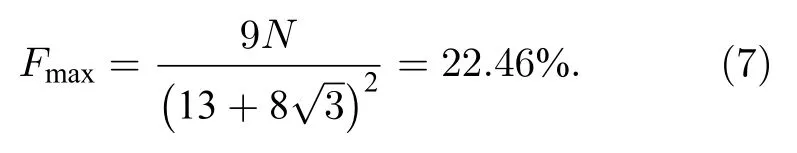
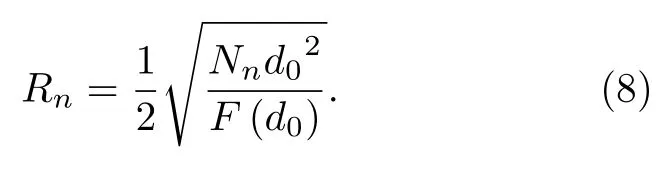
3 分形結構成像特性研究
3.1 調制傳遞函數
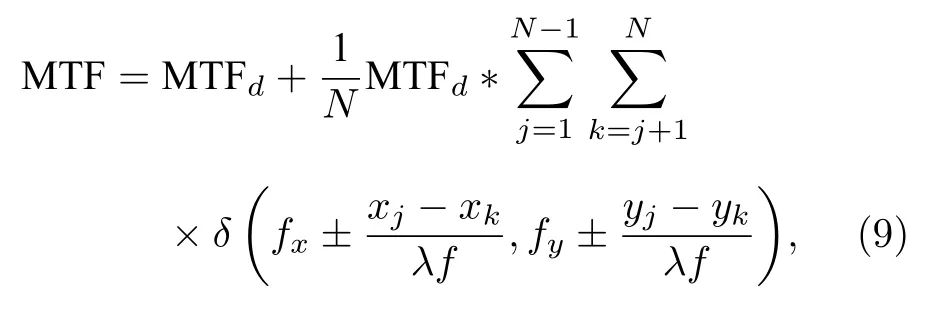

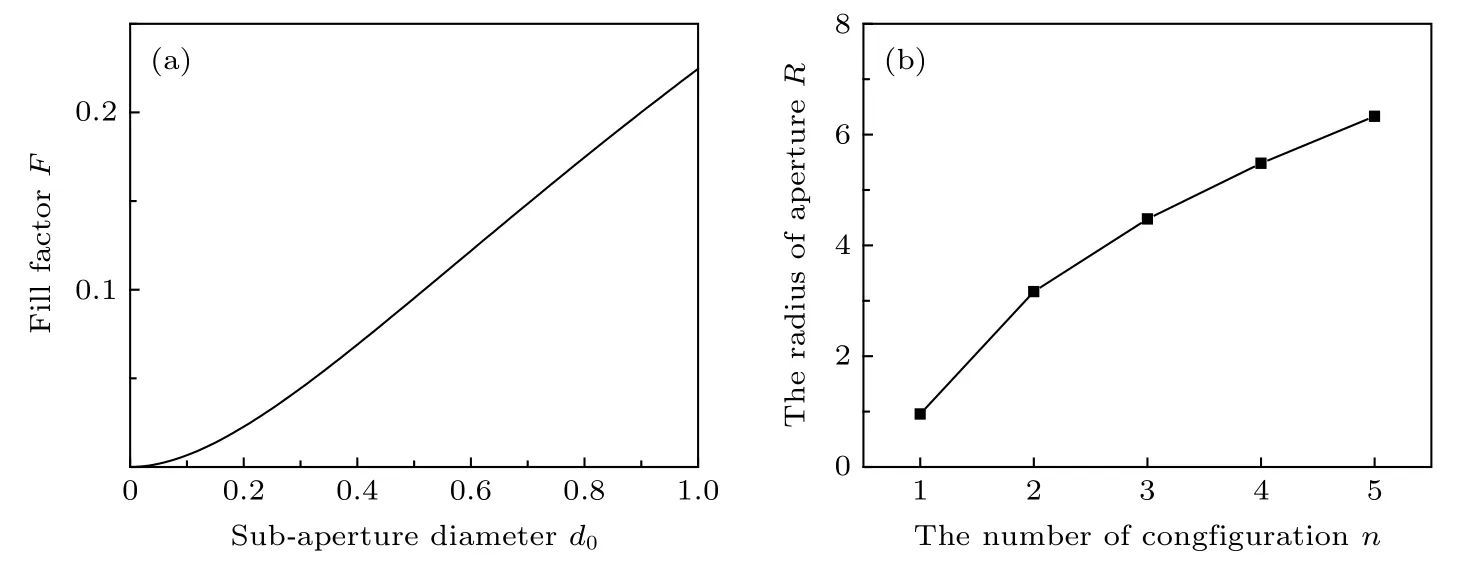
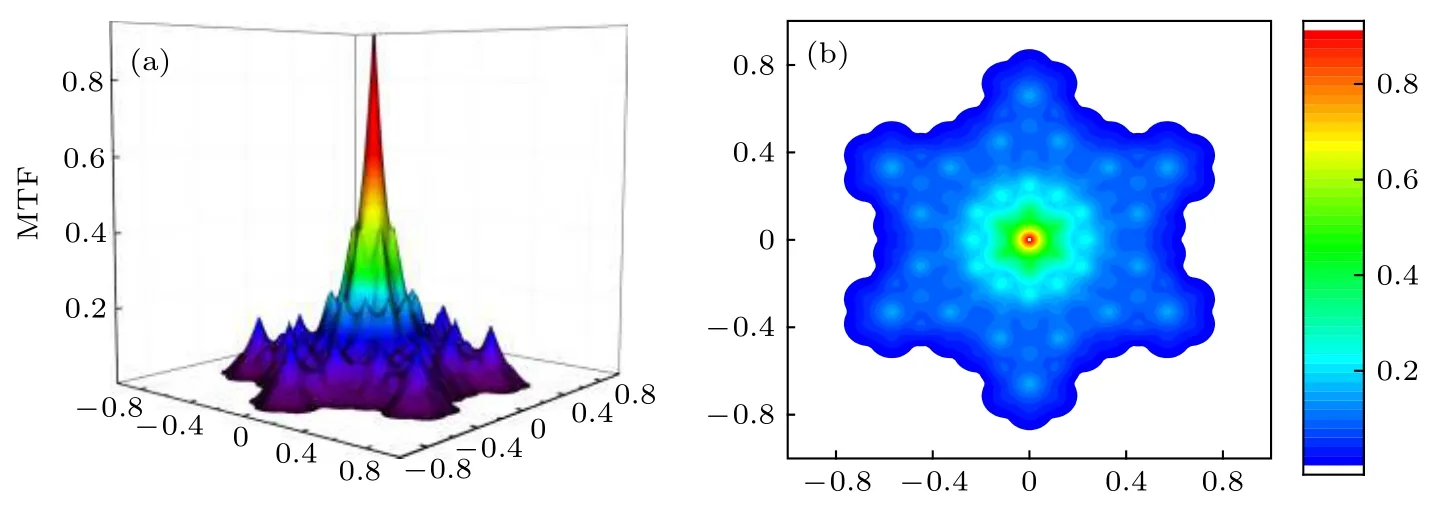
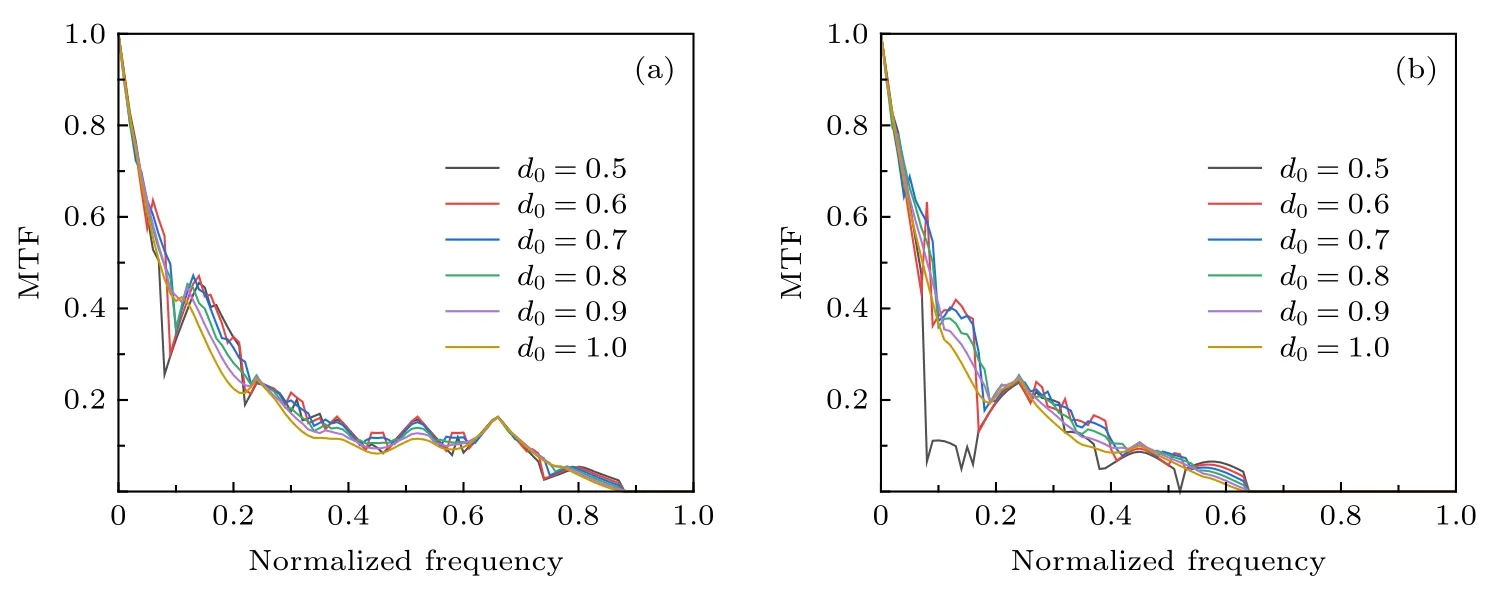
3.2 子孔徑直徑變化對MTF的影響
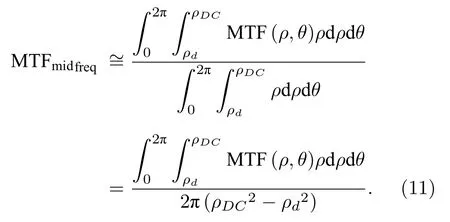
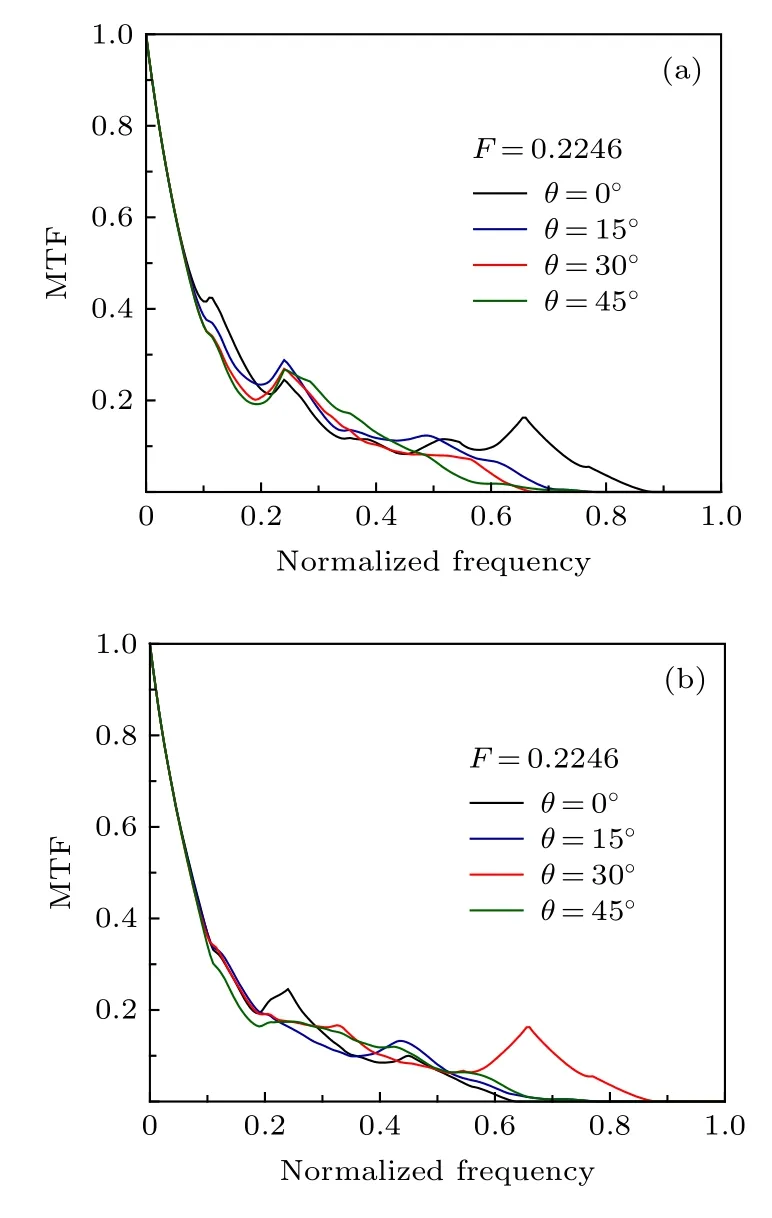
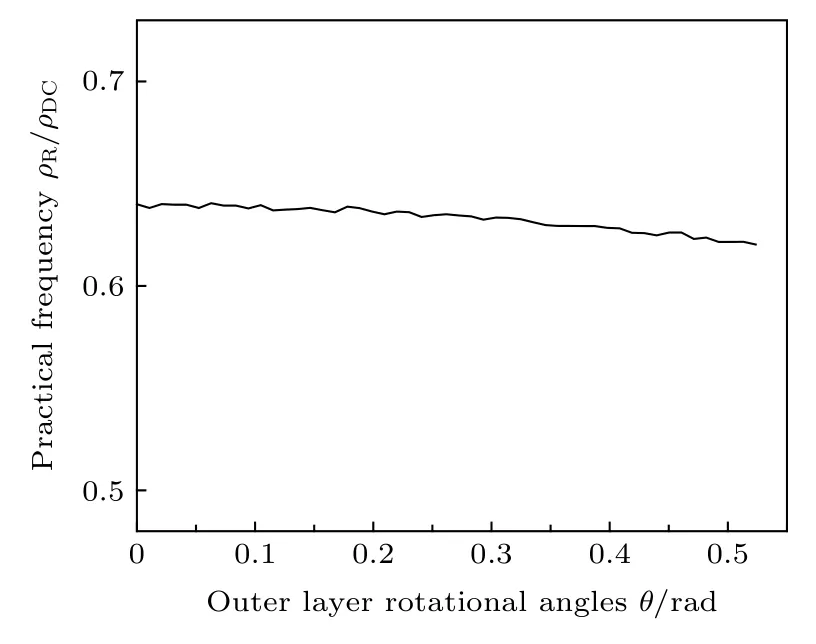
3.3 外層旋轉角對MTF的影響
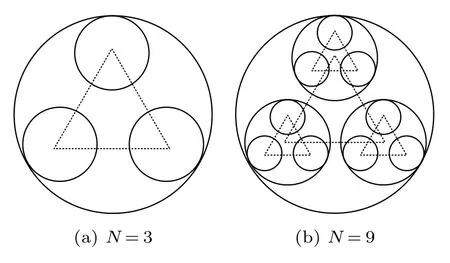
3.4 自相似結構效應


4 結 論

