光頻梳頻域干涉測距主要參數分析及一種改進的數據處理方法*
陳嘉偉 王金棟 曲興華 張福民
(天津大學, 精密測試技術及儀器國家重點實驗室, 天津 300072)
本文對光學頻率梳頻域干涉測距中的測距范圍、分辨力、非模糊范圍等的影響因素進行了分析, 并說明了傳統傅里葉變換法的局限性和系統誤差產生原因; 提出了一種等頻率間隔重采樣數據處理方法, 該方法基于三次樣條插值, 修正了傅里葉變換法因頻率量不等間隔造成的誤差; 在此基礎上提出峰值位置擬合算法,解決了包絡隨距離展寬的問題.模擬光譜儀數據并使用算法處理, 仿真結果表明系統誤差小于0.2 μm, 且可將測量范圍擴展至周期內任意位置.最后搭建經典Michelson測距系統并進行了絕對距離測量實驗, 將測量結果與干涉儀測量值進行對比, 達到了任意位置3 μm以下的誤差.
1 引 言
高精度絕對測距在當今科研、航空、工業生產等領域扮演著重要的角色, 現代工藝的不斷發展也使得人們一直在追求微米甚至納米級的絕對測距精度[1?18].飛秒激光光學頻率梳的出現為解決這一問題開辟了嶄新思路, 相關概念最早由H?nsch在1978年提出[5], 其獨特的梳狀光譜結構形成等間距分立的頻率, 溯源至銣原子鐘等基準源后可以使重復頻率frep和偏移頻率fCEO實現與外部頻率源一致的穩定度(銣原子頻率穩定度可達10–11—10–12),若將光梳對應梳齒偏頻鎖定到超窄線寬高穩定的激光, 秒級穩定度能達到10–15,形成頻率鎖定的超穩光源[4,8,19,20], 并在高精度絕對測距方面有重要應用[20,21].2000年, Minoshima 和 Matsumoto[6]首次采用鎖模飛秒激光實現了240 m大長度距離測量,其精度為 8 μm/m.此后, 飛行時間法[17,18]、合成波長法[7,12]和頻域干涉法[9,13]等利用光頻梳高相干性、頻率穩定性的測距方案被相繼提出.2006年,Joo與Kim等[9,10]提出通過光譜頻域干涉實現絕對測距的方案, 并在0.89 m測量范圍內取得了1.46 mm 非模糊范圍和 7 nm 的分辨力.2011年,Cui等[13,14]結合 Joo 和 Ye的方法, 進行了 50 m范圍大長度測距, 以測量微小位移代替光譜儀校準, 達到 1.5 μm 的測量精度, 再次證明了此方案在長距離測量中的可行性.
現有光譜頻域干涉測距算法有基于傅里葉變換法的峰值間隔法、相位斜率法和基于兩種原理的結合方案等.峰值間隔法原理簡單速度快, 以變化后的峰值位置確定疊加頻率, 但在信噪比低或頻率過低時, 頻譜因混疊而尋峰困難, 且FFT分辨力受點數限制導致數據重復.相位斜率法首先通過窗函數選定被測頻率, 再利用逆傅里葉變換解相位卷裹求得頻率, 有較高分辨力, 但濾波器的參數對結果有影響[15].同時, 由于光譜儀是等波長間隔采樣,直接處理光譜數據會導致累積性的系統誤差.
2014年, 安慰寧等[15]結合復小波理論改進了相位斜率法, 對色散等問題進行了一定修正, 在近距離范圍內取得較好的結果, 但距離較大時仍存在脈沖展寬問題, 其高精度測量范圍僅能在較小光程差內.2015年, 吳翰鐘等[16]對頻域干涉測距進行了模擬, 對相關參數進行了理論分析, 但未提及光譜儀等波長間隔采樣的問題.
為了解決上述問題, 本文對光頻梳頻域干涉測距的重要參數的影響因素、原理和現有問題進行了定性分析和推導, 根據分析結果, 提出了一種基于三次樣條插值的光譜重構算法, 該算法可增加干涉結果的信噪比, 修正傳統FFT算法系統誤差.為提升系統分辨力, 在上述算法基礎上進一步提出了峰值擬合算法, 可將測距拓展至整個非模糊范圍,減小了系統誤差并顯著提升系統分辨力.因算法復雜度低, 可用于后續實驗高速測量的實時修正和即時顯示.最后對上述算法進行了仿真和實驗驗證.
2 光頻梳頻域干涉測距原理
光學頻率梳在頻域上可以提供一系列分立的偏移頻率為fCEO, 頻率間隔為frep的頻率縱模[11],如圖1所示.

圖1 光頻梳頻譜Fig.1.Spectrum of optical frequency comb.
時域上表現為一系列等間隔的飛秒級脈沖序列, 時間間隔TR=1/frep, 群速度和相速度差異產生的載波包絡相位偏移 ?φce=2πfCEO/frep.由于光頻梳具有相位鎖定特性, 相鄰脈沖間的相位關系固定, 使不同脈沖之間可以相互干涉[16].
頻域干涉法又叫光譜干涉法或色散干涉法, 測量系統結構為經典Michelson干涉儀[11,19], 如圖2(a)所示.其中參考鏡Ref固定, 測量鏡Target可前后移動以改變光程差2L, 光頻梳發出的脈沖經分束鏡BS分束后被分別反射并產生時間差t, 再次匯聚于BS時在頻域內發生干涉, 光譜儀接收干涉信號并輸出結果.
受分光比、光路準直等因素的影響, 參考脈沖Eref(υ)和測量脈沖Et(υ) 的功率難以保證嚴格相等,表現為電場信號強度不一致, 可分別表示為:

(1)式中,a和b為對應功率因數, 理想情況下a=b且均小于1, 實際受環境等因素影響而通常不相等, 造成干涉信號I(υ) 調制深度變化:
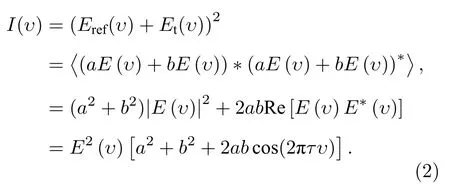
由(2)式可見直流項功率因數為a2+b2, 載波信號功率 因數 為 2ab, 調 制深 度為 2ab/a2+b2, 又 有|cos(2πτυ)|1, 僅當調制深度最大, 即a=b時,干涉條紋振蕩幅度最強, 由于空間光路的衰減效應和準直等問題, 系數b受距離影響較大, 表現為載波振蕩幅度隨L增大逐漸減小, 需及時通過衰減器調整調制深度, 避免影響信噪比.I(t) 經FFT變換后的結果為
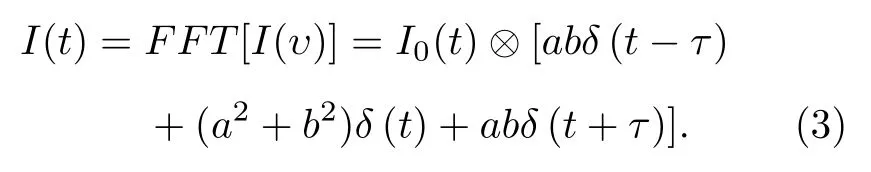
由 (3)式可知, 變換到偽時域的I(t) 將會出現δ(t?τ)和δ(t+τ) 兩沖激函數, 其中τ即為對應振蕩頻率, 即 ?t=fac[I(v)]=τ,L和t有簡單對應關系, 即L=c?t/2n=cτ/2n,n為折射率,c為光速, 對L測量等價于對t的計算.
3 主要參數分析
本節對頻域干涉中的測量范圍、距離分辨力?L、非模糊范圍LNAR的影響因素及使用原始光譜數據造成的系統誤差進行分析.

圖2 (a)頻域干涉法原理圖; (b) 測距系統實物圖Fig.2.(a) Principle of frequency domain interference method; (b) the experimental setup of the measurement system.
3.1 測量距離上下限
頻域干涉測距依靠頻譜干涉數據, 時域上的脈沖是否重合不影響測量, 根據相干長度計算公式Lc=c/n?f,?f為頻率梳的梳齒線寬, 光纖光頻梳自然線寬約為幾十kHz, 基于固體鈦寶石光梳在kHz左右, 而鎖定到超穩激光上的窄線寬光梳的線寬能達到1 Hz左右, 在相干距離內該方法僅受光強與調制深度影響, 其測距上限在真空等干擾較小的環境可達數十公里.
測距下限由干涉信號偽時域混疊程度決定,當L較小導致時延 ?t低于閾值τ0時, 將因混疊導致難以測量, 此時Lmin=cτ0/2n.
3.2 分辨力的影響因素
峰值間隔法或相位斜率法均涉及FFT變換,其分辨力受多個條件的直接影響.假設干涉結果采樣為等頻率間隔, 其頻譜范圍W和頻譜寬度B可以表示為

其中, ?w為波長范圍之差,λcen為中心波長.頻率分辨力 ?υ、采樣頻率fs和采樣點數N可分別表示為:

(5)式中, ?λ為波長采樣間隔, 得出 FFT 變換的距離分辨力 ?L為

(6) 式參數均為已知光譜的參量.由此可見, ?L僅與W有關, 改變N,fs等不影響 ?L.設定分析范圍為W= 1500—1600 nm, ?λ=0.02nm ,λcen=1560 nm, 對應N= 5000, 代入可得 ?L約為 12 μm.
由以上推導可知傅里葉變換法分辨力僅受光頻梳頻譜寬度影響.
3.3 非模糊范圍的影響因素
頻域干涉法的非模糊范圍LNAR與光譜儀的頻率分辨力df和光頻梳光譜參數均有關, 理想情況下LNAR0僅與frep有關:

由(3)式可將干涉信號I(υ) 簡要表示為
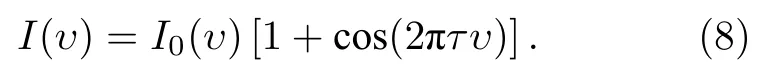
由于τ受L影響, 通常在L較大時τ遠大于光譜儀的 df而進入死區, df與波長微分量 dλ的關系為:
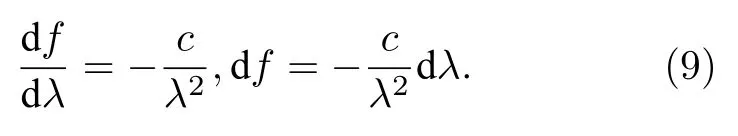
fs與采樣間隔互為倒數關系, 結合 Nyquist定律,t值域為 [ 0,1/2df] , 因此LNAR1滿足:

由 (10) 式可知,LNAR1僅與 dλ和λ相關, 代入計算可得LNAR1<28mm ; 另外, 由于反射鏡使光路往返,L的計算還應再乘1/2以獲得絕對距離.提升LNAR可采用兩種方式:可使用更大波長分辨力的光譜儀, 或是采用高frep的光頻梳, 如國內可實現frep=40GHz 及以上的片上微諧振腔光梳[1,22],其梳齒密度低, 時域上相鄰脈沖間距可達7.5 mm,可得frep與LNAR關系, 如圖3 所示.

圖3 實測距離與被測距離關系Fig.3.Relationship between actual distance and measured distance.
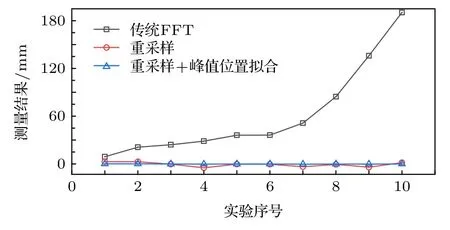
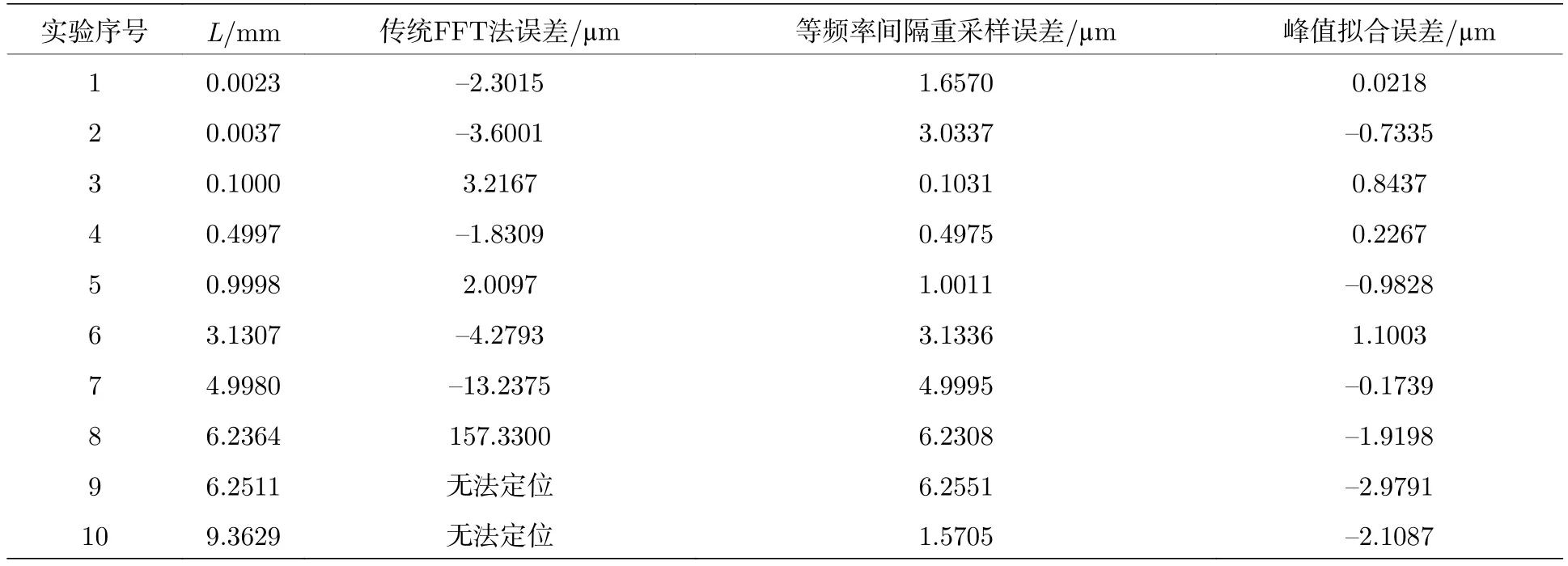
易知LNAR2 本節將分析因采樣原理而造成的系統誤差.光譜儀采樣方式有兩種:等頻率間隔 ?f采樣和等波長間隔 ?λ采樣, 絕大部分采樣方式為后者.數據處理時波長需轉化為頻率量, ?f在時域內遵從(11)式: 其中λ1為對應波長, 由 (11) 式可知, ?f由λ1決定, 且為非線性關系.由 (4)—(6)式知,f不等間隔范圍受B影響相應變化, 又因為FFT變換基于點運算, 僅適用于等間隔數據, 處理不等 ?f數據必然造成系統誤差. 由圖4 可知, 當忽略 ?f變化直接計算, 尖峰包絡隨τ增大而展寬,τ較小時展寬尚不明顯,τ較大時 ?f相應增大, 經FFT處理時因非線性造成誤差累積, 形成隨L變化且難以補償的展寬, 導致測量值漂移、信噪比下降而影響計算. 傳統FFT法和相位斜率法均應用FFT變換先行處理, 其處理的準確與否直接影響后續τ的提取:前者需定位變換后峰值所在位置, 展寬使得尖峰形狀接近原始光譜, 導致信噪比急劇下降、環境干擾更加重, 影響定位精度.后者同樣受此影響,窗函數參數對濾波效果影響較大[15], 難以控制系統誤差. 以財稅制度和法律為準繩劃清分配過程中的合法收入和非法收入,堅決取締非法收入。對誠實勞動和合法經營的高收入者,要合理調節;少數壟斷性行業的過高收入,政府要進行宏觀調控,以抑制高收入者收入的過快增長;對于非法獲得高額收入的行為依法予以打擊和取締。只有這樣,才能依法保護合法的勞動收入和非勞動收入,進一步提高社會主義市場經濟的效率和公平。 綜上, 基于FFT變換的相關算法若要解決累積性系統誤差, 必須考慮采樣方式對原始光譜數據的影響. 圖4 傳統 FFT 法脈沖包絡展寬現象 (a) τ=3.3×10?12 ; (b) τ=7.5×10?11Fig.4.Broadening of the pulse envelope using original FFT:(a) τ=3.3×10?12 ; (b) τ=7.5×10?11. 圖5 等頻率間隔重采樣原理Fig.5.Principle of equal frequency interval resampling. 本節針對上文提到的分辨力問題和頻率不等間隔問題, 提出了基于等頻率間隔重采樣法和峰值位置擬合的改進算法, 該算法修正了脈沖包絡展寬的系統誤差, 將測距范圍拓展至整個非模糊范圍,并大幅提高系統分辨力, 解決數據重復和跳變的問題. 對于因光譜儀采樣方式造成的問題, 提出了一種獲得等 ?f數據的算法.等頻率間隔重采樣基于三次樣條插值 (cubic spline interpolation), 是利用函數連續且一、二階均連續可導的特性進行的插值, 已知疊加高頻信號為固定頻率余弦函數, 此前提與(8)式符合.其原理如圖5所示. 以等 ?λ采樣值作為原始數據, 使用三次樣條插值進行光譜重構, 默認非扭結邊界條件, 再通過等 ?f點橫軸反向尋找重構函數對應值, 完成重采樣并獲得等 ?f光譜數據, 使解算更接近FFT變換原始定義, 減少原理問題導致的系統誤差. 基于傅里葉變換的算法均受分辨力影響, 數據重復原因在于 ?L大于L變化量, 即傳統FFT法僅能測量整數倍 ?L, 位置位于兩 ?L之間將使結果就近顯示, 導致τ值重復或無規律跳變, 如圖6所示. 圖6 傳統 FFT 法結果重復和跳變Fig.6.Repetition and hopping of the measurement result. 經上述處理后分辨力問題仍存在, 故誤差將呈現周期性變化, 峰值附近靠近τ形成多段折線, 如圖7(a)所示, 仿真頻率τ=3×10?11, 經重采樣修正的脈沖峰值與真實值仍有一定偏差.結合上文等頻率間隔重采樣法, 本段提出峰值位置擬合法:結合峰值點與相鄰點的微小斜率變化, 對尖峰進行二項式擬合以減小周期性誤差并提高系統分辨力. 二項式擬合基于最小二乘法, 得最小殘差平方和的二次函數, 其形式如下: 式中p1,p2,p3對應函數的二、一次項和常數項,采用峰值點和相鄰兩點這三個數據點進行二項式擬合以提取峰值附近點斜率信息, 并減小數據冗余影響, 以對稱軸橫坐標為修正值. 圖7 當 t= 3 × 10–11 時, 仿真效果對比 (a) 等頻率間隔重采樣; (b) 峰值位置擬合Fig.7.Comparison of simulation effect when t= 3 × 10–11:(a) Equal frequency interval resampling; (b) peak position fitting. 實際上, 也可采用三次多項式、高斯函數擬合等更復雜的擬合, 但在仿真及后續實驗的誤差修正效果與二項式擬合相比差異不大, 故采用在處理不同采樣分辨力、數據量的原始數據時均性能良好的二項式擬合法. 仿真采用W= 1500—1600 nm, ?λ=0.02 nm的 s ech2函數作為模擬光譜包絡, 疊加高頻余弦仿真信號, 2ab= 0.4, 頻率分別為τ=3.335×10?12,3.335×10?11, 7.500×10?11; 對 應 2L= 1.005,10.05, 22.5 mm, 如圖8 所示. 由圖8看出, 直接使用等 ?λ數據進行FFT運算, 會造成因τ變化導致的波形展寬, 而等頻率間隔重采樣法則沒有明顯的展寬, 其脈寬基本不受L影響, 對比結果見表1. 由表1可見, 等頻率間隔重采樣和峰值位置擬合的誤差遠小于傳統FFT法, 誤差基本不隨L變化, 而傳統FFT法由于頻率非線性導致累積誤差逐漸增大, 也是許多基于FFT法測距方案僅可測量較小L原因. 圖8 峰值定位仿真傳統 FFT (a) 3.335 × 10–12, (b) 3.335 × 10–11, (c) 7.500 × 10–11; 等頻率間隔重采樣和峰值位置擬合 (d)3.335 × 10–12, (e) 3.335 × 10–11, (f) 7.500 × 10–11Fig.8.Peak position fitting simulation.Original FFT:(a) 3.335 × 10–12, (b) 3.335 × 10–11, (c) 7.500 × 10–11.Equal frequency interval resampling and peak position fitting (d) 3.335 × 10–12, (e) 3.335 × 10–11, (f) 7.500 × 10–11. 表1 傳統FFT、等頻率間隔重采樣和峰值位置擬合法仿真結果誤差比較Table 1.Simulation error comparison of three methods. 由圖9可知, 因峰值位置擬合改善分辨力而減小了誤差, 在L全范圍穩定了誤差變化趨勢.彌補了傳統FFT變換引起的累積性系統誤差無法補償的缺陷, 使信號變換結果維持較窄脈寬, 擴展測量范圍, 與理論分析一致. 圖9 傳統FFT、等頻率間隔重采樣和峰值位置擬合法仿真誤差比較Fig.9.Simulation error of three methods. 圖2(b)為Michelson干涉測距的實物圖, 光源使用 Onefive Origami-15 超快激光器, 輸出frep=250MHz, 功率穩定于 50.3 mW, 輸出脈寬 130 fs,經光纖光路后脈寬受色散影響展寬至ps級.具體程度與光纖光路長度相關, 因窄脈寬包含更多的頻率縱模量, 展寬后的脈沖將損失少量頻率, 表現為光譜有效分析范圍減少.由增量干涉儀測得測量鏡Target位移量并作為準確值, 檢驗相關算法改進效果. LNAR影響因素已由前文推導,W= 1510—1610 nm, ?λ=0.01nm , 通過分析波形展寬并將測量距離與干涉儀結果相對比, 驗證等頻率間隔重采樣和峰值位置擬合法的誤差修正和對測量范圍的提升效果. 圖10 峰值定位效果對比僅傳統 FFT (a) L= 5.8600 mm, (b) L= 16.9850 mm, (c) L= 27.9100 mm; 等頻率間隔重采樣和峰值位置擬合 (d) L= 5.8600 mm, (e) L= 16.9850 mm, (f) L= 27.9100 mmFig.10.Effect contrast of peak position fitting.Original FFT:(a) L= 5.8600 mm, (b) L= 16.9850 mm, (c) L= 27.9100 mm.Equal frequency interval resampling and peak position fitting:(d) L= 5.8600 mm, (e) L= 16.9850 mm, (f) L= 27.9100 mm. 由圖10(a)—(c)可知傳統FFT法的誤差累積明顯, 超過LNAR/2 時波形展寬已不能正常計算, 本算法有效修正了該問題,L較大時仍保持明顯的窄脈沖.與干涉儀結果相比對以驗證修正效果, 見表2. 由圖10(d)—(f)和表2可知, 等頻率間隔重采樣維持窄脈寬并顯著降低尋峰難度, 峰值位置擬合在此基礎上提升了系統分辨力, 在測量范圍的任意位置穩定誤差至3 μm以下并減小了因 ?L導致的周期性誤差.其中, 實驗 1、2 相對位移小于 ?L, 傳統 FFT 法得到結果一致, 故誤差增大.另外,L較大時的展寬使原方法已不能定位, 該算法仍可保持較小誤差. 前文分析得知傅里葉變換法受限于 ?L而導致數據重復.仍使用上述光路, 改變L并測量, 與干涉儀測量值進行誤差比對, 如圖11所示. 表2 傳統FFT、等頻率間隔重采樣和峰值位置擬合法誤差比較Table 2.Measurement results of different distance. 圖11 傳統 FFT、等頻率間隔重采樣和峰值位置擬合法分辨力修正效果對比 (a) 0.4997 mm; (b) 0.9998 mm; (c) 4.9980 mmFig.11.Correction of repetition result by three methods:(a) 0.4997 mm; (b) 0.9998 mm; (c) 4.9980 mm. 圖11(a)為L= 0.4997 mm, 可明顯看出傳統FFT法所有結果重復, 重采樣不改變原有分辨力, 仍有重復結果, 峰值位置擬合處理后分辨力提升, 誤差減小至 0.3 μm 以下.圖11(b)為L=4.998 mm, 存在重復和跳變, 擬合后誤差由最大8 μm 減小至 2 μm 以下.圖11(c)為較遠距離L=4.9980 mm, 傳統方法誤差已達幾十μm并仍有重復, 本方法誤差仍小于 2 μm. 由上述實驗結果可知, 等頻率間隔重采樣和位置擬合有效修正結果重復和跳變, 系統分辨力顯著提升, 減小測量誤差并將結果抖動減小至 ?L/10 以下, 將高精度測量范圍由僅限近距離擴展至整個LNAR.本實驗系統可能仍存在機械原因導致的系統誤差, 進行誤差補償處理后可獲得更高精度測量結果. 本文詳細分析了光頻梳光譜范圍、采樣點數、采樣率等對測量分辨力的影響, 指出測距分辨力僅受光梳頻譜寬度影響.討論了非模糊范圍的影響因素, 提出了使用高分辨力光譜儀或高重頻光頻梳光源兩種解決方案.分析了傳統FFT方法的局限性,指出該方法對系統分辨力的限制.根據分析結果,本文提出一種基于等頻率間隔重采樣和峰值位置擬合的數據處理算法, 該算法可將測距拓展至整個非模糊范圍, 并大幅提高系統分辨力.仿真結果表明此方法在被測距離接近死區極限時(7.5 mm),系統誤差小于0.2 μm.我們搭建了Michelson干涉系統對所提出的方法進行實驗驗證, 結果表明該方法大大提高了系統的分辨力, 并將測量范圍拓展至整個非模糊范圍, 且在所有待測位置, 絕對誤差均小于3 μm.本文提出的數據算法大幅提高了系統的測量范圍、分辨力和測距精度, 讓光頻梳頻域干涉測距儀的商業化、儀器化成為可能. 附錄A 附表 A1 文章參數表Table A1 Parameter list.3.4 采樣方式的影響

4 等頻率間隔重采樣和峰值位置擬合算法


4.1 等頻率間隔重采樣法
4.2 峰值位置擬合算法

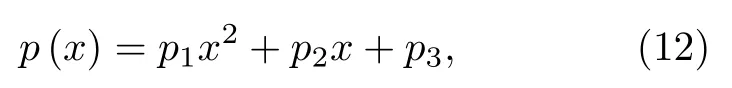

4.3 數值模擬及分析


5 實驗驗證及分析
5.1 非模糊范圍驗證

5.2 分辨力及重復性驗證

6 結 論


