基于心臟電影磁共振圖像的一種新的右心室多圖譜分割方法*

蘇新宇 王麗嘉? 朱艷春

1) (上海理工大學醫療器械與食品學院, 上海 200093)

2) (騰訊醫療健康 (深圳)有限公司, 深圳 518057)

基于心臟電影磁共振圖像的右心室(RV)分割, 對心臟疾病的診療及預后有著十分重要的意義.右心室結構復雜, 傳統圖像分割方法始終未能達到較高的精度.多圖譜方法通過配準和融合來實現RV分割, 是近幾年RV分割中的主要方法之一.本文提出一種新的右心室多圖譜分割方法, 能夠實現RV的全自動準分割.本文首先采用自適應仿射傳播算法獲取一系列圖譜集, 并基于豪斯多夫距離和歸一化互信息選擇與目標圖像最相似的圖譜集; 然后, 依次采用多分辨率的仿射變換和Diffeomorphic demons算法將目標圖像配準到最相似圖譜集, 并將配準得到的形變場應用于標記圖像獲得粗分割結果; 最后, 本文采用COLLATE算法融合粗分割結果得到RV輪廓.30例心臟電影磁共振數據被用于回顧性分析.本文算法與放射專家手工分割的RV 相比, Dice 指標和豪斯多夫距離的平均值分別為 0.84, 11.46 mm; 舒張末期容積, 收縮末期容積, 射血分數的相關系數和偏差均值分別是 0.94, 0.90, 0.86; 2.5113, –3.4783, 0.0341.與卷積神經網絡相比, 本文算法在收縮末期的分割精度更接近手動分割結果.實驗結果表明, 該方法從有效的圖譜選擇和基于多分辨率的Diffeomorphic demons算法的多級配準提高了右心室分割的精度, 有望應用于臨床輔助診斷.

1 引 言

據世界衛生組織 (world health organization)報道, 2016年大約有1790萬人死于心血管疾病,占全球死亡總數的31%[1]; 《中國心血管病報告2018》顯示, 中國心血管疾病發病率及死亡率仍處于上升階段[2].心血管疾病已經成為嚴重威脅人類健康的頭號殺手.借助影像手段評價心臟功能指標是臨床心臟疾病日常診斷的主要依據.心臟電影磁共振成像 (cine cardiac magnetic resonance imaging,Cine-CMRI)軟組織對比度高、時空分辨率好、可以動態觀察心臟解剖結構, 可重復性和高準確度使Cine-CMRI成為評估心臟功能指標的金標準.基于 Cine-CMRI的右心室 (right ventricular, RV)分割對肺動脈高壓、三尖瓣閉鎖、法洛四聯癥等心臟疾病的功能評價具有獨特的重要參考意義[3,4],是目前心臟分割領域的研究熱點.然而, RV心肌薄且個體差異大, 心外膜毗鄰脂肪, 心內膜連接小梁肌, 給傳統的分割方法帶來了不小的難度.

多圖譜分割作為目前RV分割的主要研究手段之一, 在近年來取得了長足的發展.多圖譜分割方法主要是通過圖譜先驗信息將圖像分割問題轉換為圖像配準和融合, 主要包括圖譜選擇、配準和融合三個步驟.RV多圖譜分割中, 圖譜多是主觀選擇的結構清晰的固定的圖像, 并未考慮目標圖像與圖譜集的相似性對配準精度的影響.聚類作為研究分類問題的一種統計分析方法, 可有效選擇相似圖譜.仿射傳播聚類 (affinity propagation clustering,AP)算法將數據點對之間的相似性作為輸入度量,利用數據點之間的信息傳遞得到一組高質量的聚類中心和相應的集群[5], 被首次用于RV多圖譜分割中圖譜集的獲取[6].與固定圖譜相比, AP算法避免了所有圖譜圖像與目標圖像的配準過程, 顯著減少了分割時間, 且同時提高了分割精度.但是, 圖譜圖像聚類過程時間過長、心尖圖像的分割效果不佳仍然是目前存在的問題.自適應仿射傳播聚類(Adaptive AP)算法在AP算法的基礎上進行改進, 主要包括三個方面:自動調整偏向參數的大小來搜索聚類集群數量尋找最優聚類結果; 自適應調整阻尼因子來消除振蕩; 以及阻尼效果不佳時, 降低偏向參數逃離振蕩, 以尋找出最優聚類結果[7].

醫學圖像配準是指通過尋找某種空間變換, 使兩幅圖像相似度最大化的過程.降低計算量、提高魯棒性、更精確地描述器官或組織間的形態差異,一直是備受關注的問題.Cine-CMRI圖像中, RV隨時間進行周期性的變化、并且個體結構差異巨大, 對配準方法的靈活性、精度和計算效率的要求更高.自由形變 (free-form deformations, FFD)模型是心臟等運動器官常常采用的配準方法, 該模型作為參數非剛性配準方法, 主要采用幾何平滑函數, 通過控制網格點的移動和插值優化等近似求得圖像形變, 魯棒性和精度之間的平衡由控制點網格間距和正則化量控制.大量文獻研究表明[8?12],FFD將圖像形變參數化表示, 雖然降低了計算量,但也限制了形變的復雜程度.通過局部形變近似求得整體形變, 容易產生物理折疊, 不能確保圖像的拓撲結構.對于形變較大的心臟圖像來說, FFD并不能實現精確配準.Thirion[13]根據麥克斯韋妖的原理首先提出將無參數非剛性配準視為擴散過程,以圖像梯度信息作為驅動力實現配準過程的Demons方法.Demons作為小形變配準模型, 在計算效率和配準效果方面皆表現出良好的性能, 然而傳統Demons只將參考圖像的梯度信息作為驅動力[14], 導致形變程度不高、魯棒性差, 最重要的是不能維持其拓撲結構.為了克服上述局限性,Vercauteren 等[15]提出 Diffeomorphic demons模型, 結合李群空間實現優化策略確保形變場具有拓撲保持性, 同時采用快速計算指數映射實現了對大形變配準的高效性和魯棒性, 更適用于處理心臟圖像.

融合的主要目標是在有效利用資源的情況下盡可能提供準確可靠的結果.RV配準后的標記圖像需要通過融合算法得到RV分割結果.融合算法中使用較多的是多數投票法、加權投票法、概率圖譜、STAPLE (simultaneous truth and performance level estimation)和 COLLATE (consensus level,labeler accuracy and truth estimation)算法.目前多數使用后兩種融合方法, COLLATE是對STAPLE算法的改進, 基于最大似然/最大后驗方法估計每個體素的共識水平和每個區域的性能, 從而得到更接近真實結果的估計值.COLLATE在模擬數據集和經驗數據集中取得的結果都顯著優于以往的融合方法[16].

針對RV分割存在的問題, 本文提出了一種新的RV多圖譜分割框架, 主要包括圖譜集選擇, 圖譜集與目標圖像配準得到粗分割結果, 以及融合粗分割結果獲得最終RV分割結果三個步驟.本文在圖譜制作中采用基于豪斯多夫距離和歸一化互信息的Adaptive AP算法[7]獲取一系列初始的圖譜集, 并再次根據豪斯多夫距離和歸一化互信息從初始圖譜集中選出最相似的圖譜集; 然后, 本文利用Diffeomorphic demons算法將目標圖像與最相似的圖譜集進行配準, 得到一系列保持較好拓撲結構的粗分割結果; 最后, COLLATE算法將粗分割結果進行融合, 獲得精確、魯棒的RV輪廓.

2 基礎方法概述

2.1 AP算法

AP算法通過識別具有代表性的樣本子集對數據進行聚類.s(i,k) 表示數據點i與數據點k之間的相似性, 通常使用歐式距離s(i,k)=?||xi?xk||2.s(k,k)作為輸入, 其大小影響聚類中心的選擇, 因此又被稱為偏向參數p(preferences).當所有的數據點都同樣適合作為聚類中心,p通常被設置為相似值的均值以控制生成的集群數量.吸引度r(i,k)和歸屬度a(i,k) 是數據點之間的兩種消息交換方式, 按照以下公式迭代更新:

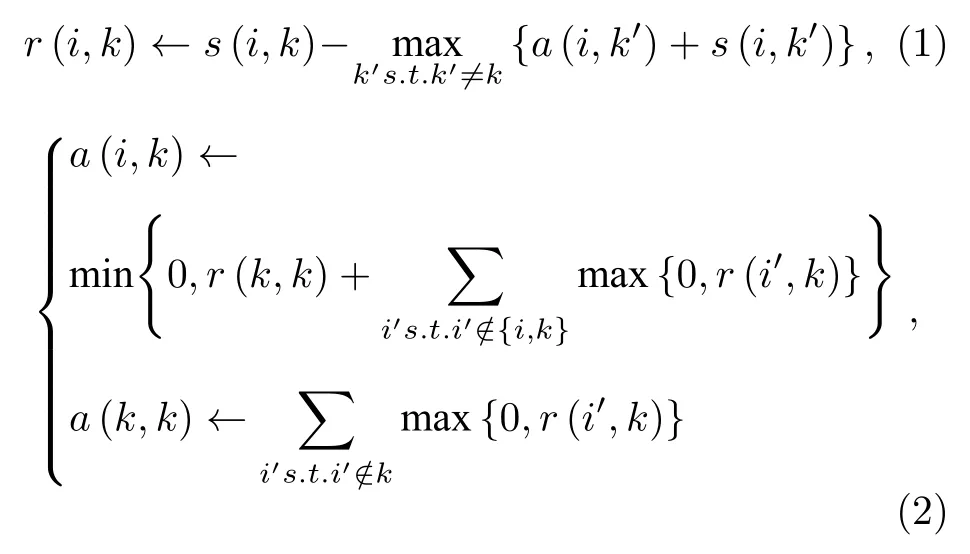
其中歸屬度初始化a(i,k)=0.在仿射傳播過程中,每一個數據點都將通過吸引度與歸屬度之和來確定是否作為聚類中心.更新消息時, 為避免出現數值振蕩設置阻尼系數λ, 更新結果由上一次迭代結果和當前迭代結果加權得到,λ和 1 ?λ分別為二者權重, 默認值為 0.5.與其他方法相比, AP 算法更加精確、高效, 并應用于人臉圖像聚類、基因檢測、文本識別等領域.

Adaptive AP在AP算法的基礎上提出自動消除振蕩的方法和自動調整偏向參數的大小以尋找最優的聚類結果, 具體步驟如下:1) AP 算法進行一次循環, 產生k個類代表, 并檢測是否振蕩;2)若發生振蕩, 則逐步增大阻尼因子λ, 否則轉步驟1); 3)檢測k個類代表是否收斂, 若不收斂轉步驟1); 4)繼續若干次循環以驗證結果是否穩定, 結果穩定逐漸減小偏向參數p, 否則轉步驟1); 5)重復以上步驟直至達到停止條件.相比較于AP算法, Adaptive AP在聚類質量和消除振蕩方面具有更優或不低于原算法的結果.

2.2 Diffeomorphic demons算法

Diffeomorphic demons是目前醫學圖像中常用的一種高效、魯棒的非剛性配準算法, 通過使全局能量函數最小化實現最終的配準過程.該方法分為優化過程和正則化過程, 其中, 優化過程采用的全局能量函數的標準形式如下[15]:

其中F為參考圖像,M為浮動圖像,σi2為圖像的噪聲大小,σx2為形變場正則化的程度,s為上一次迭代后的形變,u為迭代更新的形變場,表示作為相似性測度的均方誤差表示形變場的誤差函數.而正則化過程一般通過高斯卷積完成, 得到流體模型或擴散模型的正則化效果.

對于圖像中任意一點p的形變, 可通過最小化全局能量函數得到:

通過(4)式計算圖像的形變場, 并在李群中實現形變場的復合得到最終的配準結果圖像.由于每次迭代都需要計算形變場的指數映射 e x(p(u) ,)因此利用單參數子群的性質 e xp(u)=expK?1uK和SS (scaling and squaring method)快速計算:

1) 選擇一個N, 讓 2?N趨近于零, 例如

2) 對圖像中任意一點p:v(p)←2?Nu(p) ,對v做N次復合運算v←v?v;其中,v1與v2并不是簡單相加, 而是通過v2驅動形變, 重新插值得到和v2再相加得到.

Diffeomorphic demons算法步驟如下:

1) 給定目標圖像F和圖譜圖像M, 仿射變換后的形變場s作為初始形變場;

2) 通過最小化E, 即(4)式計算更新后的形變場u;

3) 對u做高斯卷積, 讓u←Kfluid?u, 產生流體模型的正則化效果;

4) 讓c←s?exp(u) ;

5) 對c做高斯卷積, 讓s←Kdiff?c, 產生擴散模型的正則化效果;

6) 重復以上步驟, 直至E收斂或達到最大迭代次數, 得到最終形變場s及配準結果.

Diffeomorphic demons是在李群框架下實現配準的優化策略, 可以產生具有微分同胚的形變、保證RV配準中產生的變形場具有可逆性、拓撲保持性.

2.3 COLLATE算法

COLLATE作為一種統計標簽融合算法, 可以準確估計和解釋空間變化的性能.假設一幅圖像有N個像素點,R個標簽信息用來評估其真實結果.D為N×R的矩陣, 描述所有N個體素中所有R個配準結果的標記決策.設T為N個元素的向量, 表示所有體素的隱式真分割, 其中Ti{0,1,···,L? 1}.定義一個包含N個元素的向量C, 它表示在每個體素的一致或混淆特征, 共有F個等級,Ci∈ {0,1,···,F? 1}.定義θ=[θ1,θ2,···,θR], 表示R個配準結果對應的性能水平估計; 結合上述定義, 將f(D,T,C|θ) 定義為概率質量分布函數, 并通過最大期望算法 (E-M algorithm, EM) 來實現性能水平參數θ的估計, 其中, E-Step 將估計圖像體素i屬于每個一致性水平的概率, 這個概率在M-Step中估計性能水平參數時對每個體素的權重至關重要.COLLATE作為一種準確、魯棒的融合算法, 已經成功用于RV分割[17].因此提出使用COLLATE算法進行RV標記圖像的融合.

3 一種新的RV多圖譜分割框架

本文提出了結合Diffeomorphic demons算法的多圖譜分割框架, 從心臟磁共振圖像中自動精確提取RV輪廓, 一系列圖像處理流程如圖1所示.算法具體步驟如下:

1) 原始心臟磁共振數據首先進行預處理, 通過霍夫圓變換定位左心室并確定包含RV的感興趣區域;

2) 依據圖像特征和灰度信息進行仿射傳播聚類得到圖譜集, 并根據目標圖像選擇圖譜集;

3) 然后與圖譜圖像分別進行仿射變換和Diffeomorphic demons配準, 并將得到的形變場應用于標記圖像;

4) 最后利用COLLATE算法融合所有標記圖像得到右心室分割結果.

基于以上提出的方法對心臟磁共振圖像進行處理.從RV特征及結構出發, 考慮在RV分割中感興趣區域過大, 導致計算量增加從而降低分割速度, 同時影響圖像的配準及分割效果, 尤其是心尖部分.同舒張末期 (endo-diastolic, ED)相比, 收縮末期 (endo-systolic, ES)的 RV 輪廓較小.因此,本文采用不同大小的感興趣區域進行處理:123 ×123, 103 × 103.從空間結構來看, 基底到頂端心室面積逐漸減小, 分割也越來越困難.所以, 本文在預處理階段將心室基底到頂端的感興趣區域逐漸縮小, 具體通過定位左心室中心, 縮小半徑來實現.這樣既解決了由于感興趣區域過大引起的計算量增加和配準精確性等問題, 同時頂端心室腔狹小難以分割的問題也得到緩解.

3.1 圖譜集選擇

本文結合Adaptive AP算法和圖譜集特點提出適合RV分割的圖譜聚類方法, 具體流程如圖2所示.

圖譜集包括圖譜圖像和標記圖像, 其中標記圖像是由專家手動勾畫RV輪廓得到的二值圖像.針對圖譜集的特點, 采用不同的相似性測度進行分別聚類.首先, 標記圖像l1?ln采用豪斯多夫距離(Hausdorff distance, HD)作為相似性度量進行Adaptive AP 聚 類, 得 到 結 果C1(l),C2(l),···,Cm(l); 取相應的圖譜圖像子集C1(g),C2(g),···,Cm(g)采用歸一化互信息(normal mutual information)作為相似性度量分別進行Adaptive AP聚類, 得到進一步的聚類子集C1(g),C2(g),...,Ck(g).多圖譜在圖譜數量的選擇要平衡分割精度和速度之間的關系, 研究表明圖譜數量在15—20幅范圍之間, 可以保證分割精度的同時提高速度[18].因此, 我們將子集數量是否大于等于15作為滿足條件進行篩選, 最后將符合要求的聚類子集再一次進行聚類, 得到一組聚類中心g1,g2,···,gi;l1,l2,···,li和集群C1(g),C2(g),···,Ci(g);C1(l),C2(l),···,Ci(l).

圖1 結合多圖譜和 Diffeomorphic demons 算法的右心室分割流程圖Fig.1.Flow diagram of right ventricular segmentation combined with multi-atlas and Diffeomorphic demons algorithm.

圖2 圖譜圖像聚類流程圖Fig.2.Atlas image clustering flow chart.

聚類后針對目標圖像選擇合適的圖譜集進行分割.首先目標圖像T與i個聚類中心經配準、融合得到初始分割結果L; 然后依據相似性測度的大小選擇圖譜集.文獻[5]使用了Dice系數作為選擇依據, 但是其只考慮了L與l1,l2,···,li的重疊區域的大小.本文從配準算法出發, 考慮其驅動力主要依靠圖像梯度信息提出了一個新的相似性測度:

其中 HD代表豪斯多夫距離, 測量標記圖像l1,l2,···,li與L之間最大差異的對稱距離度量.NMI代表歸一化互信息, 測量兩幅圖像的灰度相似性.D表示相似性測度, 由 HD 和 NMI共同決定 ,α和 1 ?α代表二者的權重.計算目標圖像T與各聚類中心的相似性測度, 選擇相似性最高的聚類中心所代表的圖譜集用于接下來的RV分割.

在圖譜選擇階段, 頂端心室面積太小可能會導致圖譜集選擇失敗.對于這些無法選擇圖譜集的層面提出一種替代策略, 即選擇上一層面的圖譜集作為分割圖譜.這是由于心臟磁共振電影圖像相鄰層面之間具有較大的相似性, 替代策略可以減小由于心室面積過小而導致分割失敗的概率并保證其分割精度.

3.2 配準和融合

Diffeomorphic demons算法保證了配準前后的拓撲保持性, 高效、靈活的計算方式對心臟圖像的大形變配準表現出良好的性能.為了提高結果的魯棒性, 在進行 Diffeomorphic demons 配準之前,首先對兩幅圖像進行仿射變換, 得到粗配準結果.圖3是RV配準的典型例子, 可以看出Diffeomorphic demons在RV圖像配準中取得了較好的結果.

圖3 四個右心室配準的典型例子 (a) 目標圖像; (b) 圖譜圖像; (b) 標記圖像; (d) 配準結果Fig.3.Four examples of typical right ventricular registration:(a) Target image; (b) atlas image; (c) label image; (d)registration result.

為了進一步提高配準速度, 結合了多分辨率策略, 首先圖譜圖像和目標圖像在最低分辨率情況下進行配準, 快速得到該分辨率層的形變場; 然后該形變場進行上采樣作為更高分辨率層的初始值, 以加快配準速度, 重復以上步驟直到得到最終的形變場.

COLLATE算法可以依據標簽信息準確估計圖像空間變化.本文在右心室的多圖譜分割中將配準步驟得到的標記圖像利用COLLATE算法進行融合, 得到準確、魯棒的分割結果.RV標記圖像的融合過程如圖4所示.

圖4 RV 標記圖像的融合過程Fig.4.RV label image fusion process.

4 實驗結果與對比

4.1 實驗數據

Cine-CMRI短軸圖像在GE1.5 T掃描儀上通過SSFP序列獲取, 采集8—16層連續的電影短軸切片以覆蓋整個心室.具體成像參數:圖像矩陣大小 256 × 256, FOV 是 360 mm × 360 mm, 層厚6—8 mm, 層間距 2—4 mm, 一個完整的心動周期包括20—28個時相.數據來源者均簽署知情同意書.隨機選取34例短軸電影圖像, 由專家手動勾畫出ED, ES時相的RV輪廓, 該標記圖像用于圖譜制作.另外隨機選取30例數據用于算法驗證,同時將專家手動勾畫得到的RV輪廓作為金標準,用于實驗結果評估.

4.2 評估指標

分割結果的評估是圖像分割的重要步驟, 本文采用互補的兩個客觀指標對分割結果進行評估:幾何指標和臨床表現, 綜合兩種評估指標可以防止對分割結果的片面評估, 保證評估結果的客觀性和準確性.定量評估金標準與算法分割結果的幾何指標包括:Dice指標和豪斯多夫距離.Dice指標是兩個區域重疊的度量, 其范圍在0—1之間:

其中Sa,Sb分別代表自動分割算法和金標準中的RV區域.Dice指標越高代表算法分割與金標準之間的重合程度越高.豪斯多夫距離提供了兩個標記輪廓之間最大差異的對稱距離度量, 定義為:

其中A,B表示自動分割算法和金標準的RV輪廓,a和b分別表示輪廓A和B中的點,d(a,b) 代表歐幾里得距離.

通過RV分割量化的心臟功能指標主要包括舒張末期容積 (end diastolic volume, EDV), 收縮末期容積 (end systolic volume, ESV)及射血分數(ejection fraction, EF).臨床表現是將心臟功能指標的算法結果與臨床數據進行一致性和相關性分析.其中, 相關性分析主要是描述算法結果與臨床數據的相關密切程度.一致性通過 Bland-Altman圖實現, 算法結果與臨床數據的偏差均值(Mean)及一致性界限(Mean ± 1.96SD)是衡量二者一致性的主要依據.

4.3 實驗結果

本文對30例臨床心臟磁共振數據進行處理,并與專家手動勾畫的金標準進行比較.ED及ES的典型分割如圖5和圖6所示, 圖中依次是RV的基底到頂端.

表1給出了 RV分割結果在 ED和 ES的Dice指數和HD, 其中數據以均值(方差)形式呈現.表中數據可以得到ED及ES的Dice指標平均為 0.87, 0.81; ED和 ES的 HD平均為 10.76和12.16 mm.從結果比較, ED 的分割結果與金標準的重合度更高.與現有分割方法存在的問題相同,ES時相的分割結果精度相對較低.主要原因是ED時相RV結構簡單, 邊界清晰; 而ES時相由于部分容積效應導致邊界模糊且心室腔相對較小, 分割難度更高.30例分割結果的Dice指標箱形圖如圖7所示, 其中 ED, ES的中位數分別為 0.875,0.820.從圖中可以看出ED時相的分割結果優于ES時相, 且分割結果更加穩定.

圖5 ED 從基底到頂端的 RV 分割結果Fig.5.RV contour at ED from base to apex.

圖6 ES 從基底到頂端的 RV 分割結果Fig.6.RV contour at ES from base to apex.

表1 ED, ES 的平均 Dice 指數和豪斯多夫距離Table 1.Average Dice index and Hausdorff distance of ED and ES.

圖7 Dice 指標的箱形圖Fig.7.Box diagram of the Dice index.

分析30例數據結果與金標準的相關性和一致性, 結果如圖8所示, 圖中Data表示30例數據結果.圖8(a)、(c)、(e)表明自動分割結果與金標準的相關性, 其中橫縱坐標分別為金標準和自動分割算法的結果,y表示線性回歸方程并在圖中標出.EDV, ESV 及 EF 的相關系數R分別為 0.94, 0.90,0.86.其中, EDV的結果與真實臨床指標的相關性最高.圖8(b)、(d)、(f)顯示了 EDV, ESV 及 EF的自動分割結果與金標準具有較高的一致性.圖中橫軸為自動分割結果和金標準的均值, 縱軸為自動分割結果和金標準的差值.Mean是差值的平均值,SD 表示差值的標準差, Mean ± 1.96SD 為一致性界限.Bland-Altman 圖中表明, EDV, ESV 及 EF的偏差均值分別是 2.5113, –3.4783, 0.0341, 可以看出自動分割算法偏差很小, 除了少數的異常值,所有的測量值都在一致性界限內.從相關系數和偏差均值來看, ED 比 ES 提高了 0.04, 0.967, 表明ED的分割結果更加接近金標準, 這是由于舒張末期心室面積相對較大.一致性分析顯示ES時RV容積輕度低估, 主要原因是ES頂部心室面積狹小, 部分圖像未分割出RV輪廓.

為了進一步驗證算法分割結果的準確性, 將算法結果與深度學習的全自動分割結果進行了比較.其中, 深度學習分割是由Circle CardioVascular Imaging (http://www.circlecvi.com/)開發的心臟分析軟件心血管成像(CVI)得到.卷積神經網絡是CVI分割心臟圖像的主要方法, 其結果的準確性也已得到驗證[19,20].圖9為深度學習結果與金標準的相關性及Bland-Altman分析(圖中各符號物理意 義 均 同 圖8).EDV, ESV, EF 的 相關 系數R分別為 0.93, 0.86, 0.66, 與本文算法得到的相關系數 0.94, 0.90, 0.86 相比, 深度學習方法的 ESV 和EF 的一致性水平明顯偏低.圖9(b)、(d)、(f)中偏差均值分別為–1.8167, –6.1830, 0.0372, 可以看出,ES的偏差均值相對較低.相比之下, 本文算法的偏差均值 2.5113, –3.4783, 0.0341 相對平均, 算法的穩定性更高.與深度學習相比, 本文提出的算法在ES階段具有較高的分割精度, 主要是依據ES的結構特點在預處理及圖譜選擇階段做出了調整.然而, ED時相的分割結果相對較差, 是由于深度學習依據大量數據訓練得到的更具代表性的分割模型, 結果精確度更高.

圖8 本文算法與金標準結果分析 相關性分析 (a) 舒張末期容積; (b) 收縮末期容積; (c) 射血分數; Bland-Altman 分析 (d) 舒張末期容積; (e) 收縮末期容積; (f) 射血分數Fig.8.Analysis of algorithm and gold standard results.Correlation analysis (a) EDV; (b) ESV; (c) EF; Bland-Altman analysis (d)EDV; (e) ESV; (f) EF.

5 結 論

圖9 深度學習與金標準結果分析 相關性分析 (a) 舒張末期容積; (b) 收縮末期容積; (c) 射血分數; Bland-Altman 分析 (d) 舒張末期容積; (e) 收縮末期容積; (f) 射血分數Fig.9.Analysis of deep learning and gold standard results.Correlation analysis (a) EDV; (b) ESV; (c) EF; Bland-Altman analysis(d) EDV; (e) ESV; (f) EF.

RV復雜結構和Cine-CMRI的影像學特點是其分割的主要困難:RV內包括隨心動周期變化的乳頭肌和小梁肌; 部分容積效應和心臟運動常導致Cine-CMRI短軸圖像的低信噪比.在基底部,可以觀察到RV, LV, 心房及周圍結構往往難以區分, 導致 RV邊界不確定.在心室頂端, 心室腔狹窄且心肌及內部結構分布不均, 分割更加困難.針對這些問題, 提出一種從心臟磁共振短軸圖像中自動分割RV的新方法.該方法采用多圖譜框架和Diffeomorphic demons算法結合, 并且依據豪斯多夫距離和歸一化互信息采用Adaptive AP獲得圖譜集.實驗結果表明, 該方法取得了與金標準具有較高一致性的分割結果, 無論在幾何指標和臨床表現中, 都成功驗證了方法的可行性和準確性.與其他現有方法比較, 我們提出的方法可以做到準確、快速地分割出RV輪廓, 具有更強的魯棒性和準確性, 特別是心室腔狹小的圖像.提出的新方法有望輔助臨床心臟疾病的診斷、治療和預后.同時, 為了更好地提高分割效果, 還可以結合圖像特征進一步優化配準算法, 提高多圖譜分割精度和速度將是下一步要做的工作.