淺談數學史和數學故事在數學課堂中的滲透
李靜
摘 要:數學史和數學故事能幫助學生了解數學的歷史、應用和發展趨勢,考察數學對象的歷史演變,總結前人的經驗教訓,對學生學習數學知識有一定的啟發作用。本文通過幾個案例闡述數學史與數學故事在數學課堂中的運用。
關鍵詞:數學史;數學故事;數學課堂
我國教育部在新的中學課程標準中指出:“數學課程要適當地反映數學的歷史、應用和發展趨勢,數學課程應幫助學生了解數學在人類文明發展史中的作用,逐步形成正確的數學觀”。那么在數學課堂教學中,根據教材的內容,適當的在課堂中引入數學史和數學故事,有利于學生了解數學、接受數學、學習數學并應用數學。接下來將從幾個案例談談數學史和數學故事在數學課堂中的滲透。
案例1數學源于生活,用于生活
很多同學在學習數學的過程中,覺得數學對于我們現實生活好像作用不大,像函數、各種計算、證明題,要么抽象難懂,要么枯燥無味,但是除了考試,似乎也用不上。其實不然,數學不是憑空出現的,它源于生活,用于生活,在課堂教學中,我們可以適當的介紹一些數學史或數學故事,講講這些內容的起源。
比如,函數的來源,與我們日常生活中的“運動”有關,人們在思索:既然地球不是宇宙中心,它本身又有自轉和公轉,那么下降的物體為什么不發生偏斜而還要垂直下落到地球上?行星運行的軌道是橢圓,原理是什么?還有,研究在地球表面上拋射物體的路線、射程和所能達到的高度,以及炮彈速度對于高度和射程的影響;而在迫切需要發展航海和軍火工業時期,為了發展航海事業,就需要確定船只在大海中的位置,在地球上的經緯度;要打仗,也需知道如何使炮彈打的準確無誤等問題,這些都促成了函數概念的產生。
案例2無理數概念學習中介紹無理數的發展
在課堂教學中,通過一個有趣的小視頻來講故事《無理數的發現-----希伯索斯的冤案》:古希臘時期畢達哥拉斯學派認為“萬物皆數”,通過一些研究,他們認為世界上一切現象只能用數學才能加以解釋,都能歸結為整數或整數之比,在畢達哥拉斯時代,人們對有理數的認識不是很清楚,對于無理數的概念更是一無所知,他們所說的數,僅僅是指整數,這時,學派中的成員希伯索斯利用勾股定理,用邏輯推理的方法發現,邊長為1的正方形,對角線的長度既不是整數,也不是整數比能表示的,這個發現嚴重觸犯了畢達哥拉斯學派的信條,對于只有整數和整數比概念的他們來說,邊長為1的正方形對角線無法用任何“數”來表示,這件事在數學史上稱為第一次數學危機,希伯索斯的發現沒有被畢達哥拉斯學派的信徒們所接受,相傳因為這一發現,他被畢達哥拉斯學派的信徒投入大海處死了。
后人用反證法證明了希伯索斯的發現是正確的,證明如下:設邊長為1的正方形長度可表示為,其中a,b是既約的正整數,則根據勾股定理可得,即,這表明b2是一個偶數,因而b也是偶數(否則,b為奇數,設b=2k+1,則也是奇數,矛盾)。設b=2k,則,,即是偶數,因而a也是偶數,那么m,n都有公約數2,這與假設矛盾。
最終無理數被確認下來了。
案例3古題今用,啟迪思維
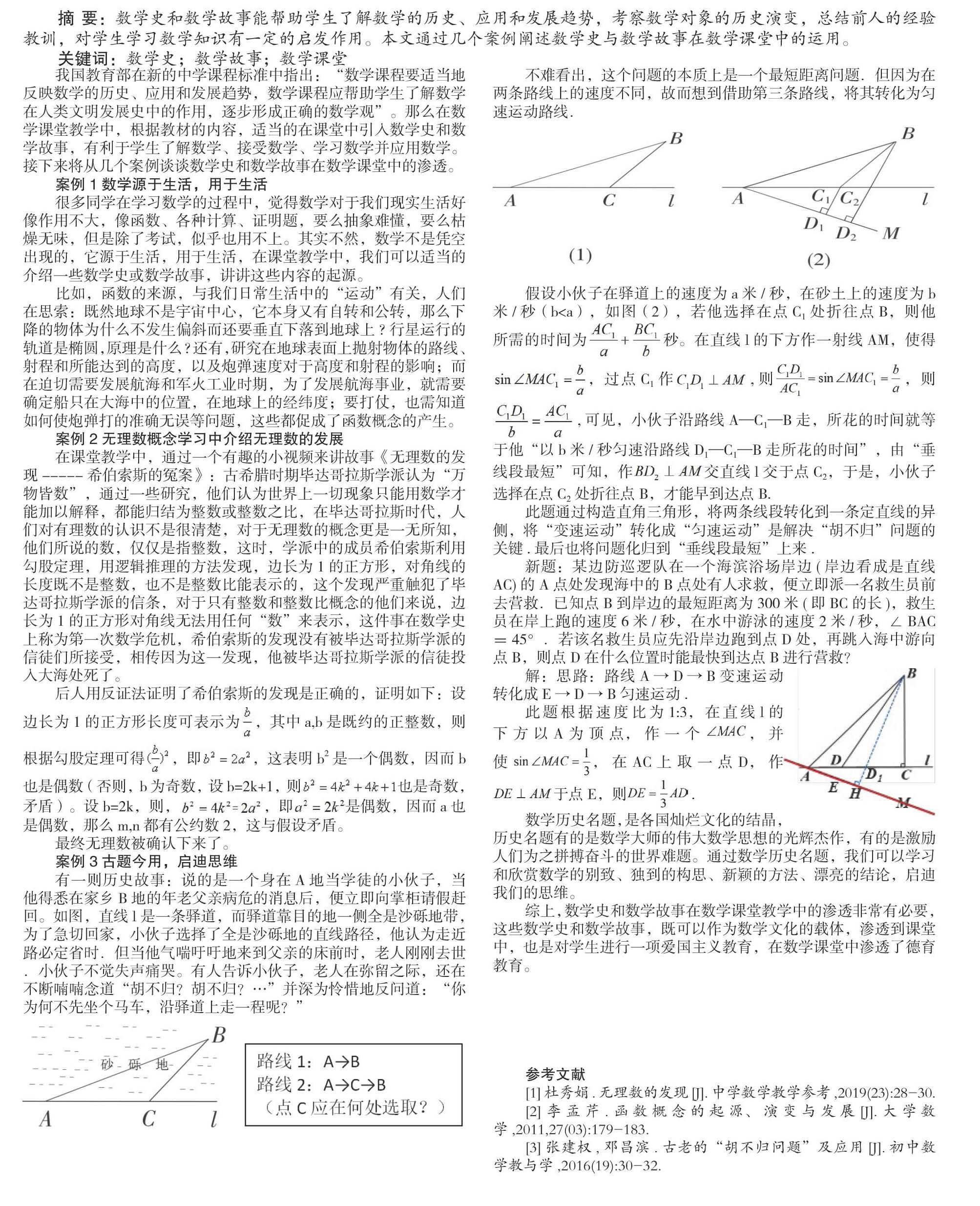
有一則歷史故事:說的是一個身在A地當學徒的小伙子,當他得悉在家鄉B地的年老父親病危的消息后,便立即向掌柜請假趕回。如圖,直線l是一條驛道,而驛道靠目的地一側全是沙礫地帶,為了急切回家,小伙子選擇了全是沙礫地的直線路徑,他認為走近路必定省時.但當他氣喘吁吁地來到父親的床前時,老人剛剛去世.小伙子不覺失聲痛哭。有人告訴小伙子,老人在彌留之際,還在不斷喃喃念道“胡不歸?胡不歸?…”并深為憐惜地反問道:“你為何不先坐個馬車,沿驛道上走一程呢?”
不難看出,這個問題的本質上是一個最短距離問題.但因為在兩條路線上的速度不同,故而想到借助第三條路線,將其轉化為勻速運動路線.
假設小伙子在驛道上的速度為a米/秒,在砂土上的速度為b米/秒(b 此題通過構造直角三角形,將兩條線段轉化到一條定直線的異側,將“變速運動”轉化成“勻速運動”是解決“胡不歸”問題的關鍵.最后也將問題化歸到“垂線段最短”上來. 新題:某邊防巡邏隊在一個海濱浴場岸邊(岸邊看成是直線AC)的A點處發現海中的B點處有人求救,便立即派一名救生員前去營救.已知點B到岸邊的最短距離為300米(即BC的長),救生員在岸上跑的速度6米/秒,在水中游泳的速度2米/秒,∠BAC=45°.若該名救生員應先沿岸邊跑到點D處,再跳入海中游向點B,則點D在什么位置時能最快到達點B進行營救? 解:思路:路線A→D→B變速運動轉化成E→D→B勻速運動. 此題根據速度比為1:3,在直線l的下方以A為頂點,作一個,并使,在AC上取一點D,作于點E,則. 數學歷史名題,是各國燦爛文化的結晶,歷史名題有的是數學大師的偉大數學思想的光輝杰作,有的是激勵人們為之拼搏奮斗的世界難題。通過數學歷史名題,我們可以學習和欣賞數學的別致、獨到的構思、新穎的方法、漂亮的結論,啟迪我們的思維。 綜上,數學史和數學故事在數學課堂教學中的滲透非常有必要,這些數學史和數學故事,既可以作為數學文化的載體,滲透到課堂中,也是對學生進行一項愛國主義教育,在數學課堂中滲透了德育教育。 參考文獻 [1]杜秀娟.無理數的發現[J].中學數學教學參考,2019(23):28-30. [2]李孟芹.函數概念的起源、演變與發展[J].大學數學,2011,27(03):179-183. [3]張建權,鄧昌濱.古老的“胡不歸問題”及應用[J].初中數學教與學,2016(19):30-32.

