動車組設備螺栓連接可靠性分析

李暢 呂志龍 周安德

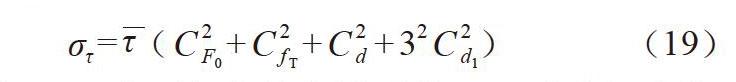
摘 要：提出以概率論和數理統計為基礎的可靠性設計方法，明確可靠性分析的必要性、其相對于傳統安全系數法的優勢、可靠性分析的應力-強度干涉模型等。采用該方法設計驗證某動車組項目底架設備上的螺栓連接可靠性，通過可靠性分析指出當前設計的不合理之處，為之后的設計工作提供思路;利用可靠性原理發現目前螺栓生產應用中對可靠度影響比較大的關鍵參數，結果表明摩擦系數的分散度對可靠性的影響最大，其次是材料強度分散度，而螺栓直徑和長度尺寸分散度對可靠性的影響較小，基本可以忽略。

關鍵詞：動車組;螺栓連接;干涉模型;關鍵參數;可靠性分析

中圖分類號：U27;TH12

0 引言

隨著社會的發展進步，交通運輸業在國民經濟中的地位變得愈發重要。在動車組整體系統結構中，主變壓器、變流器、制動風缸及控制系統等較大的電氣設備，通常采用螺栓連接的方式懸掛在列車底部，因此螺栓連接的可靠性是生產組裝動車組過程中必須要保證的關鍵項。螺栓連接設計有2點注意：①選擇合理的連接緊固件;②對裝配時的預緊力進行控制。相對于歐美及日本，我國鐵路交通運輸業發展起步相對較晚，在螺栓連接設計方面還有一定差距，比如國內公司目前大多通過項目類比的方法選取緊固件，擰緊扭矩的施加值也直接采用以前車型的數值，缺少針對具體車型及應用的分析，這樣容易導致螺栓在使用過程中失效。

可靠性是指產品在一定條件和時間下無故障執行一定功能的能力，一般可通過可靠度、失效率和平均無故障間隔等參數表示，防過載、松動可靠性及抗疲勞可靠性構成了螺栓連接可靠性的主要內容。采用常規的安全系數法設計時，工程師對安全系數的選擇存在個人主觀性，為了追求安全，通常將安全系數取的較大，進而選取優質材料或加大尺寸，由此造成了資源的浪費和機械結構的笨重。傳統的安全系數法將應力、強度等作為單值確定變量進行計算，表達方式相對簡單直觀，這也是其一直沿用至今的原因。但是實際上螺栓工作應力、材料強度、螺栓尺寸等因素都是呈一定規律變化的變量，存在一定的分散性。可靠性設計是以概率論和數理統計為基礎，通過掌握應力和強度等的分散規律來預測螺栓失效的概率。

上述2種設計方法提高螺栓連接可靠性的思路不同。安全系數法實際只能設法控制應力和強度的均值，而可靠性設計可以控制影響因素的均值和標準差。從這個角度看，可靠性設計方法通常比安全系數法更合理。但是可靠性設計需要積累大量的統計資料，比如結構材料基本性能的統計分析，螺栓連接可能出現的失效模式及隨時間變化的規律等，因此可靠性設計初期可能會耗費更多的精力和費用。隨著資料的積累、設計經驗的豐富，這種情況就會得到改善，企業效益、社會效益也會逐步顯示出來。所以，可靠性設計越來越被企業所重視，也是今后發展的方向。

1 可靠性分析的原理

實際工程應用中，螺栓連接件的工作應力和材料強度呈一定規律變化，不是定值。根據長期的現場使用經驗和統計研究，在機械結構中發生的失效通常符合正態分布規律。因此，可以采用正態分布對螺栓連接的可靠性進行有效的預計或估算。

分析螺栓連接的可靠性，實質上可以概括為2方面的影響因素：工作應力和材料強度。根據可靠性理論，螺栓發生故障失效的原因就是工作應力大于材料的強度。

由概率論可知概率密度分布函數f（x）是累積故障分布函數F（x）的導數。假設工作應力x的概率密度函數為f（x），材料強度y的概率密度函數為g（y）。根據上文分析，螺栓正常工作時的應力應當小于螺栓材料的強度。但由于工作應力和材料強度的分布符合正態分布規律，它們的離散性造成工作應力和材料強度的概率密度函數曲線在一定條件下存在相交的可能性，從圖1中可以看出相交的干涉部分表示強度可能小于應力，此時螺栓可能發生故障失效。通常把這種干涉模式稱為應力-強度干涉模型。

分析干涉模型可知，通過采取措施減小圖中干涉的陰影面積就可以提高螺栓連接的可靠性。顯然有2種思路可以減小陰影面積，一種是通過減小螺栓受力可以使f（x）左移，或使用高性能等級的材料使g（y）右移;另一種思路就是減小螺栓工作應力和材料強度的分散度，讓它們的概率密度函數變的“瘦高”，如圖2所示。工作載荷通常一定，采用太大的安全系數會增大連接結構，提高材料性能也不利于企業控制成本，所以應盡量降低應力和強度的概率密度函數的分散度，來提高螺栓連接的可靠性。

值得注意的是，即使螺栓的工作應力和材料強度在螺栓工作前期階段沒有產生干涉的陰影部分，但隨著螺栓工作服役時間的累積，在動載荷、磨損、腐蝕、疲勞載荷的長期作用下，螺栓材料的強度也會逐漸降低使g（y）左移，從而和f（x）相交而產生干涉。顯然隨著螺栓工作時間的累積，連接的可靠度也會逐漸降低直至失效。因此，僅采用常規的安全系數法進行設計計算是不夠的，這正是其與可靠性設計法最重要的區別。螺栓連接可靠性設計的本質就是得到工作應力和材料強度的分布規律，嚴格控制發生失效的概率，以滿足設計要求。

設工作應力x和材料強度y的概率密度函數為：

（1）

（2）

式（1）、式（2）中，μx 、μy分別為應力和強度的均值;σx、σy為應力和強度的標準差。令z = y - x，由于應力和強度均服從正態分布，則根據正態分布的加法定理可知，隨機變量z（-∞

（3）

式（3）中，隨機變量z的均值μz = μy - μx;標準差。

當y>x時，螺栓連接可靠，其可靠度R為：

（4）

令，則dz = σzdβ，當z = 0時，β的下限為：

（5）

式（5）將應力分布、強度分布和可靠度三者聯系在一起，稱為聯結方程，是可靠度設計中的1個重要表達式。β稱為聯結系數，又稱為可靠度系數。利用此式可求出β，通過查閱標準正態分布表即得可靠度的值，也可以用給定的R求得β。

當Z→+∞時，β的上限也是+∞，因此：

（6）

顯然隨機變量也是標準正態分布，由于標準正態分布的對稱性，因此可靠度也可寫為：

（7）

設Cx、Cy分別為應力和強度的變異系數，SR為可靠性安全系數，則：

（8）

（9）

將以上兩式帶入聯結方程可得到可靠性安全系數SR和聯結系數β之間的關系為：

（10）

（11）

2 可靠性分析的實例

材料強度指標主要指材料的抗拉強度σb和屈服強度σS，兩者均能較好地符合或接近于正態分布。但應注意，目前國內鋼材標準中的抗拉強度和屈服強度數據，大都是置信下限為90%的保證值，因此考慮它們的變異系數，抗拉強度和屈服強度的均值應為：= 10.7σb、 = 1.1σS。σb 、σS均為可以在有關手冊上查到的保證值。

本部分以公司常用的不銹鋼材料螺栓為例進行分析，借以闡明可靠性分析的計算思路、步驟、設計方法等內容。

可靠性設計的一般步驟如下。

（1） 計算螺栓的工作荷載F。根據設計條件估算螺栓連接副的工作荷載均值 和標準差σF。一般在工程應用中，通常取公差為3倍的標準差，即3σ原則。所以，標準差可按載荷的容許偏差估算，之后即可求得變異系數CF。

（12）

（13）

式（12）中， F max為螺栓最大工作荷載; F min為螺栓最小工作荷載。

（2）計算螺栓總拉力F2。螺栓總拉力既要滿足預緊力的要求，又要滿足最小殘余預緊力的要求，總拉力通常取以下2式中的最大值。

2≥（1 + C 2）F? ? ? ? ? ? ? ? ? ? ? ? ? （14）

2≥（ x + C 1）F? ? ? ? ? ? ? ? ? ? ? ? ? ?（15）

式（14）、式（15）中，F為工作荷載; x為螺栓的相對剛度;系數C 1、C 2的取值范圍見表1。F2的標準差σF2可近似取σF2≈2×CF。

（3）根據螺栓連接副中螺栓個數（隨機變量Z），計算螺栓拉應力σt和切應力τ及其標準差和變異系數。

螺栓拉應力標準差為：

（16）

式（16）中，d1 為螺栓危險截面直徑。

切應力標準差為：

（17）

式（17）中，為螺栓公稱直徑均值;0為預緊力的均值;T為當量摩擦系數均值，其中f T = 0.02 + 0.5 f，f為螺紋間的摩擦系數。

當量摩擦系數的變異系數為：

（18）

式（18）中，σ f為摩擦系數的標準差。

螺栓拉應力為：

στ = （ C 2F0 + C 2 f T + C 2d + 32 C 2d1）? ? ? ? ? ? ? ? （19）

式（19）中， CF0為預緊力的變異系數; Cf T為當量摩擦系數的變異系數; Cd為公稱直徑的變異系數; Cd1為螺栓危險截面直徑的變異系數。

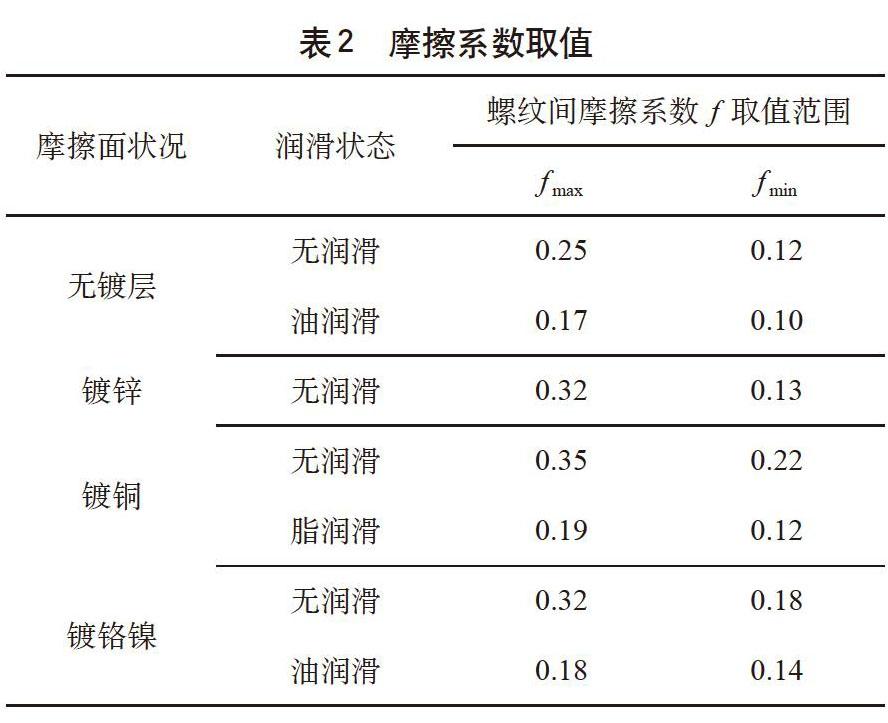
上述式中摩擦系數的相關取值可在表2中查出。

（4）根據第四強度理論計算復合應力σca的均值與標準差。

（20）

（21）

（5）選擇螺栓的材料，確定強度分布的均值和標準差。

（6）用聯結方程按可靠度要求確定螺栓直徑或者按已有的設計計算可靠度。

這里以某動車組項目底架懸掛設備連接螺栓為例進行可靠性分析：制動控制單元閥G閥質量為58±

1.74kg，通過4個M10×60不銹鋼螺栓懸掛于車底C型槽內，螺栓材料為A4-80并采用了A4材料的鎖緊墊圈。依據上文的計算方法，可得聯結系數。根據正態分布的知識可知當β≥4.9時，可靠度R即可達到1.0，此例中的β = 19.79>>4.9，因此在本實例中，螺栓連接的可靠度為1.0。這時以螺栓的屈服極限為基準的安全系數 。

通過計算結果可以看出，使用A4-80的螺栓連接造成了螺栓材料性能的極大浪費，同時也提高了企業生產成本，因此是不合理的設計。另外，在本項目底架設備螺栓連接中，制動控制單元閥S閥（55kg）、BTM（信號接收天線）組裝（44kg）、附加風缸（24.5kg）、接地電阻組裝（4.8kg）的受力均比給出的實例小，但也使用了A4-80的M10×60螺栓，所以這種選型同樣不合理。針對以上幾種設備的懸掛螺栓連接，完全可以采用鈍化處理的低等級中碳鋼或者低合金鋼制作的螺栓進行連接，既充分發揮螺栓材料性能，又能節省生產成本。

為了闡明公稱直徑、螺栓危險截面直徑、抗拉強度、摩擦系數等幾個關鍵參數對可靠性影響的大小，這里以車頂母線支持絕緣子連接螺栓M12×25進行分析，其材料為A2-70。在GB/T 3098.6-2000《緊固件機械性能 不銹鋼螺栓、螺釘和螺柱》及GB/T 5783-2016《六角頭螺栓 全螺紋》中規定，其螺紋應力截面積As = 84.3mm，機械性能抗拉強度σb = 700MPa，公稱直徑d = 12mm，螺栓危險截面直徑d1 = 10.106mm，長度l = 25±0.42mm，根據表2可知摩擦系數f= 0.12～0.25。取加工偏差為0.02。以3σ原則考慮可得公稱直徑、危險截面直徑、長度和摩擦系數的標準差。計算各參數的標準差及變異系數如下：

σσb = 37.45MPa，σd = 0.08mm，σd1 =0.067mm，σ1 = 0.014mm，σf= 0.017

Cσb = 5.00%，Cd = 0.667%，Cd1 = 0.663%，C1 = 0.056%，Cf= 8.95%

通過比較各參數的變異系數可以看到，摩擦系數的分散度最大，其次是抗拉強度;螺栓長度的分散度最小，基本可以忽略;螺栓公稱直徑和危險截面直徑的分散度幾乎相同，這主要是由加工方法決定的。因此在實際生產應用時，對螺栓連接可靠性影響的敏感程度排序為：摩擦系數>抗拉強度>公稱直徑>危險截面直徑>螺栓長度。所以為了在螺栓使用過程中提高可靠度，應當對螺栓、螺母、墊片之間相對硬度的配合、潤滑劑的選用等進行適當調整，從而減小摩擦系數的離散程度。此外，通過嚴格控制原材料質量、熱處理工藝和硬度檢測分選也可減小材料強度的離散程度。在螺栓加工過程中嚴格控制加工工藝，減小螺栓直徑的離散程度也可提高螺栓可靠度。

3 結語

可靠性設計以概率論和數理統計為基礎，可以得到螺栓失效的概率，即可靠度，可靠性設計法比傳統的安全系數法更合理。螺栓的失效情況符合正態分布規律，利用應力-強度干涉模型可知，通過減小螺栓工作參數的分散度可以有效地提高螺栓連接的可靠度。實例結果表明，目前的螺栓應用選型存在未能充分發揮螺栓效能及成本高等問題，應結合本文提出的計算方法，針對關鍵參數采取相應控制措施。

參考文獻

[1]文強，張博言. 動車組設備安裝用螺栓扭矩計算及強度校核[J]. 機械工程師，2014（4）：229-300.

[2]周潔. 安全系數與可靠性[J]. 機械設計與制造，1999（5）：3-5.

[3]侯亞萍. 螺紋聯接的防松方法[J]. 機械工程師，2010（7）：18-19.

[4]李巧良. 可靠性工程師手冊[M]. 北京：中國人民大學出版社，2012.

[5]李毅華，汪正俊. 機械設計中安全系數與可靠性的研究[J]. 煤礦機械，2002（1）：22-24.

[6]齊昭田， 崔靈芝. 受拉螺栓聯接可靠性設計計算方法的研究[J]. 天津科技大學學報，1999（3）：46-49.

[7]連喜軍， 強寶剛. 螺栓聯接的可靠性設計[J]. 遼東學院學報（自然科學版），2006，13（4）.

[8]趙秀文， 李明， 王暉. 受軸向載荷緊螺栓聯接的可靠性設計[J]. 吉林工學院學報（自然科學版），1999（3）：35-38.

[9]王磊. MEMS器件可靠性分析設計軟件的開發[D]. 江蘇南京：東南大學，2009.

[10] 張洪才. 應力-強度干涉模型的可靠度計算方法的研究[J]. 機械設計，2001（6）：45-47.

[11] 楊娜，葉國銘. 機械可靠性定性與定量方法概述[J]. 機械設計與制造，2006（3）：16-18.

[12] 付陟瑋，張巧娥，宋大虎. 核電廠機械設備可靠度計算方法探索[J]. 原子能科學技術，2018，52（10）.

[13] 張西應，顏驥，任亞東. 應力-強度干涉模型在功率半導體器件失效分析中的應用[J]. 大功率變流技術，2016（1）：34-38.

[14] 羅松松，田志軍，鄧斌，等. 基于模糊數學的接觸網零部件可靠度計算模型[J]. 機械設計與制造，2008（12）：52-54.

[15] 王佩艷，朱振濤，王富生，等. 復合材料螺栓連接性能的分散性和可靠性分析[J]. 力學季刊，2008，29（4）：573-577.

[16] 劉忠偉，劉少軍，黃明輝，等. 基于模糊可靠度的巨型模鍛水壓機主工作缸缸體的優化設計[J]. 重型機械，2007（2）：29-35.

[17] 郭敏. 高強度螺栓的可靠性分析[J].機械制造，1990（1）：10-12.

[18] GB/T 3098.6-2000 緊固件機械性能 不銹鋼螺栓、螺釘和螺柱[S]. 2000.

[19] GB/T 5783-2016 六角頭螺栓 全螺紋[S]. 2016.

收稿日期 2019-03-20

責任編輯 孫銳嬌