基于SVM的蒸發量預測因子組合與模型研究

程才華

（山西水利職業技術學院，山西 太原 030027）

據統計我國現有2 474個國家級地面站，國土面積963萬km2，氣象站覆蓋率低，且現有的氣象站存在嚴重的蒸發數據缺測情況，現有的蒸發資料難以滿足農田灌溉及水文預報的需求[1-3]。已有學者針對蒸發數據不足的問題展開了蒸發量預測研究，但研究的時間尺度較短，預測過程中缺乏對各氣象因子與蒸發量關系的考慮，對于長期蒸發量預測成果的合理性與可行性有待評估[4-5]。文章以山西長治氣象站為例，首先以該氣象站2015-2016年的日氣象數據為基礎，利用灰色關聯法得到蒸發量與其他氣象因子之間的關聯程度，對影響蒸發量的主要氣象因子進行篩選，并輸入主要氣象因子，輸出相應時段的蒸發量數據，為作為構建蒸發量SVM預測模型的基礎，研究在不同氣象因子組合下模型預測精度的變化，研究氣象因子的選取及組合對模型預測效果的影響。

1 數據來源

長治站基礎氣象數據源于中國氣象科學數據共享服務網，氣象數據包括長治站2015—2017年的日系列蒸發量（EVP）、平均風速（WIN）、逐日日照時數（SSD）、逐日平均氣溫（TEM）、逐日平均相對濕度（RHU）、逐日20～20時累計降水量（PRE）。

2 理論依據

2.1 灰色關聯度排序及輸入因子選擇

各氣象因子與蒸發量關聯程度信息量及數據量均較少，而灰色關聯方法可利用灰色關聯度來描述因素間關系的強弱，可有效解決信息量貧瘠數據量少的問題。因此本研究以灰色關聯理論確定了各氣象因子對蒸發量作用的大小[7]，為蒸發量預測模型輸入因子的合理確定提供依據。

2.2 預測模型

本文選取支持向量機（SVM）神經網絡模型對蒸發量進行預測[8-9]。預測應用非線性回歸算法。最優分類回歸方程為：

式中，ω為權系數向量，φ（x）為映射關系，b為閾值。

對于給定的訓練樣本集合{（x1，y1），（x2，y2），…，（xn，yn）}，其函數形式為：

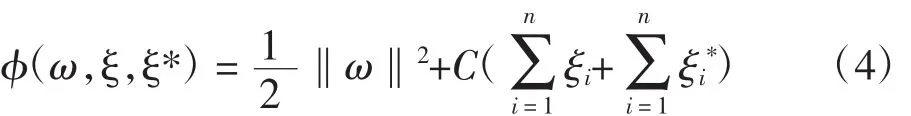
對應的約束條件為：

式中，C用于衡模型精度和復雜度，為懲罰因子；ε為不敏感損失函數；ξi為松弛變量的上限為松弛變量的下限。

判定函數通過Lagrange因子法來描述優化問題：

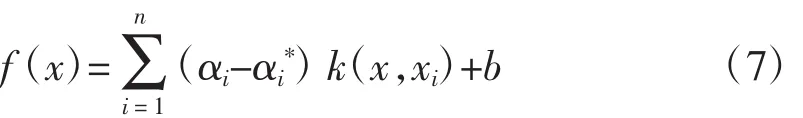
式中，αi（i=1，2，…，l）為Lagrange因子；K（x，xi）為向量機核函數；

本次研究所用預報模型為高斯核函數：

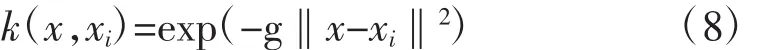
本研究支持向量機模型利用Libsvm工具箱，在Matlab環境下建立。

2.3 評定標準

本研究選擇常用的預測精度評價指標均方根誤差RMSE及決定系數R2對預測效果進行評價。其中：

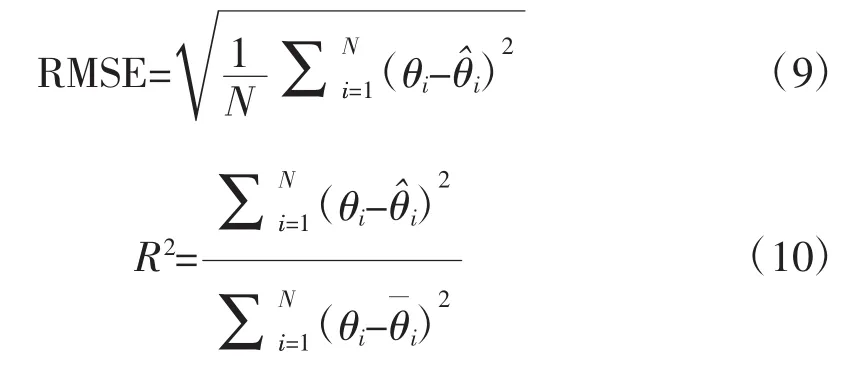
式中，N代表樣本數量，θi和分別代表代實測值和預測值代表實測值的平均值。RMSE越小R2越大，預測精度越高。

3 蒸發量影響因子分析

利用灰色關聯理論計算得到影響蒸發量的5個參數對蒸發量的關聯度，如表1所示。一般認為關聯度大于等于0.8時，序列間的關聯顯著[6]。本研究所用5個氣象因子與蒸發量都表現出顯著的關聯性（＞0.8），表明本研究所選取的5個氣象因子都是影響蒸發量的重要因素，可作為預測模型的輸入。

表1 關聯系數計算結果表

4 模型的預測精度對比

分析可知，本研究所選擇的5個氣象因子都是影響蒸發量的重要因素，預測模型輸入需要充分考慮這5種因子對蒸發量的影響。為研究模型在不同因子組合下的預測效果，分別構建不同數量因子組合下的預測模型，共計26組，對模型輸出結果進行檢驗，從而尋求最佳的模型輸入因子組合。預測模型由建模樣本組構成，通過調節模型參數使得輸出的預測值與實測值誤差最小，輸入建模組選擇2015—2016年逐日系列氣象因子的組合，對2015—2016年蒸發量進行預測與實測蒸發量進行對比，調節模型參數使SVM模型預測精度達到最高。將調節好的模型參數應用于2017年的蒸發量預測，以2017年相應的氣象因子組合作為所建預測模型的測試樣本，從而計算得到模型的擬合結果。

通過對26種因子組合樣本進行訓練，建立了26個蒸發量預測模型，各因子組合下的模擬效果如表2所示。由表2可知，各因子組合下的模型所得RMSE介于0.403～0.575之間，模型R2介于0.191～0.824之間，模擬效果差距較大，表明因子組合是影響蒸發量預測精度的關鍵因素，文章所建立的SVM蒸發量預測模型精度最高即R2最大取為0.824時對應的因子組合為第21組，即TEM+WIN+SSD+RHU，此時模型的RMSE值也最小為0.403；預測模型精度最低即R2最小為0.191時對應的因子組合為第10組，即RHU+PRE，此時模型的RMSE值也最大即0.575，最佳與最差模擬結果對比見圖1。這表明，對長治地區的蒸發量預測取TEM+WIN+SSD+RHU組合其結果最為可靠，接近實際情況，取RHU+PRE組合其結果較差，不能為實際提供參考。

表2 各因子組合下的模擬效果

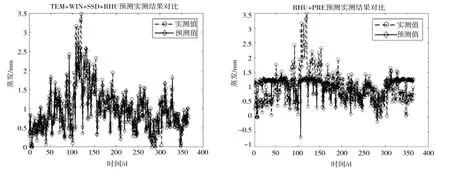
圖1 預測結果對比圖

5 結語

文章基于灰色關聯與SVM建立了20個不同因子組合下的長治地區蒸發量預測模型，對模型精度進行對比分析，得到氣象因子組合對模型模擬效果具有重大影響，在長治地區模型模擬精度最高時對應的因子組合為TEM+WIN+SSD+RHU，此時模型預測R2值0.824，RMSE值為0.403。在不同區域進行蒸發量預測時，會存在當地氣象資料不滿足最佳蒸發量預測因子組合的情況，此時借助本研究在不同區域選取所能得到的預測精度最高因子組合，對蒸發量進行預測。文章研究內容可為蒸發量預測提供新的思路，一方面有助于提高資料充足地區的蒸發量預測精度，另一方面可以為缺資料地區的蒸發量預測提供參考，未來需要對不同地區的季節性蒸發量預測模型進行研究，尋找區域性最佳預測因子組合，為蒸發量預測提供更多依據。