城軌線路車底空駛出場路徑與時刻表綜合優化

王 典，趙 軍，鐘慶偉，彭其淵

(1.西南交通大學 交通運輸與物流學院，四川 成都 611756；2.西南交通大學 綜合交通智能化國家地方聯合工程實驗室，四川 成都 611756)

本文研究城市軌道交通線路車底全日出入場走行安排中的關鍵環節，即運營時段前車底集中空駛出場路徑與時刻表綜合編制問題。城市軌道交通線路在運營時段初開行多列列車，它們始發于不同的車站，由于可供車底接續不同列車的時間有限，使得其中幾乎所有的列車都需由車場發出的車底擔當。由此，運營時段前大量車底集中從車場出發，根據指定的物理路徑和時刻表，直接空駛至其擔當列車的始發站。車底集中空駛出場安排比較靈活，每個車底既可選擇從其始發車場到其擔當列車始發站的直達路徑，也可選擇從其始發車場經1個甚至多個折返站再到其擔當列車始發站的折返路徑。然而，為確保整個出場活動的安全可行以及列車正點開車，必須保證每個車底的出場路徑和時刻表與其他車底的時空無沖突，車場和車站能力滿足要求，且出場過程需在其擔當列車開車時刻之前完成。

目前國內外在城市軌道交通線路列車運行圖和車底運用計劃編制方面開展了一定工作。運行圖編制方面，更關注時變和隨機客流需求下的動態和魯棒運行圖編制模型與算法，見文獻[1-4]。對于車底運用問題，文獻[5-6]考慮列車編組、車底解編、車底空駛和客流需求等情況，建立車底運用計劃魯棒優化模型。文獻[7]分別建立具有多交路共線運行的線路在獨立和套跑運用條件下的車底運用計劃編制模型。文獻[8]提出運營時段前車底集中空駛出場路徑優化問題，最小化總空駛距離，構建0-1線性規劃模型。第三項相關研究是公交車配屬問題，為公交車指派車場，以滿足車場能力和路線車數需求。文獻[9]考慮總空駛距離最小和最大空駛距離最小目標，提出非支配排序多目標優化算法。文獻[10]考慮配屬唯一性，提出幾個啟發式算法。文獻[11]引入車場運用均衡性和運營費用目標，設計遺傳算法。文獻[12]考慮分時段車場能力和路線車數需求，構建多階段配屬模型。

綜上，城市軌道交通線路車底集中空駛出場路徑與時刻表綜合編制尚未獲得學術界高度關注。既有列車運行圖編制研究通常提前固定列車在線路正線上的運行路徑，基于此側重于優化運營時段內列車在線路正線給定運行路徑上途經車站的到發時刻，忽略列車所需車底的出入場走行過程及其出入場路徑的多樣性(直達路徑和折返路徑)，且未全面考慮車場檢修和出車能力及折返站能力的限制，難以用于確定運營時段前車底集中出場路徑與時刻表。既有車底運用計劃研究往往設定車底出入場選擇直達路徑，主要勾畫運營時段內的車底交路，不能保證每條獲得交路上的車底均可在運營時段前通過直達路徑完成出場。文獻[8]與本文研究相似，但其只優化運營時段前車底集中出場路徑，簡單以給定時間內可發出或折返的最大車底數來刻畫車場和折返站的能力，未嚴格滿足車底出場時刻表的編制要求，注意，只確定車底出場路徑難以確保后續可勾畫出時空無沖突且高質量的車底出場時刻表。公交車配屬的既有研究一般規定車輛在車場與路線始發/終到站間按指定路徑運行，假設車輛在運行途中無時空沖突，且忽略車場和車站能力，不適用于城市軌道交通線路的車底出場安排。

鑒于此，本文根據城市軌道交通線路的運營特點，在文獻[8]的基礎上，對運營時段前車底集中空駛出場路徑與時刻表進行綜合優化，同時確定運營時段前車底從其配屬車場到其列車始發站的時空無沖突的出場路徑與時刻表，通過引入時刻表約束更為準確地描述車場的出車能力及車站的接發車能力和折返能力，從而獲得更具有運營可行性的車底出場方案。

1 問題定義

1.1 問題描述

城市軌道交通線路運營時段前車底空駛出場路徑與時刻表綜合優化包含路徑與時刻表優化兩個子問題：給定線路運營時段內的列車運行圖和車底交路，路徑問題在于指派運營時段初各列車需要車底的配屬車場及運營時段前從車場到列車始發站的出場路徑；給定出場路徑，時刻表問題在于確定各車底在選擇路徑上途經各車場、中間站和折返站的到發時刻。鑒于現場存在多種運營條件的城市軌道交通線路，不失一般性，本文針對復雜的具有多車場、多車型和多列車交路的線路開展研究，該線路可約簡為更為簡單的線路。

以包含6個車站(含4個折返站)和2個車場的線路為例進行問題描述，如圖1所示，其中車站沿下行方向從s1到s6依次編號，車場類似編號為j1和j2，其所在站分別為車站s2和s5。線路沿線設置4個折返站，分別為s1，s3，s5和s6。車站s1為單向站后折返站，可將車底由上行折返為下行。車站s3為雙向站前折返站，可折返兩個方向車底。車站s5為單向站后折返站，可將車底由下行折返為上行，該站連接車場，通常運營時段前不辦理折返作業。車站s6為單向站前折返站，可將車底由下行折返為上行，下行車底直接接入上行正線進行折返。

線路運營2條列車交路，第一條的端點為車站s1和s6，第二條的為車站s3和s6。線路在6：30開始運營，根據提前編制的運營時段內的車底交路計劃，運營時段初下行列車i1和上行列車i2和i3需由在運營時段前空駛出場的車底擔當，列車i1屬于第二條列車交路，列車i2和i3屬于第一條列車交路。現需為擔當該3列列車的車底指派配屬車場、出場路徑及時刻表(統稱出場方案)，在滿足各種運營和能力要求的條件下，減少車底總空駛距離和總空駛時間。

圖2提供一些候選車底空駛出場方案，可以看出，若忽略車場檢修及出車能力、車站和折返站能力，根據車場和折返站位置以及列車始發站和發車方向，可確定任意列車的所有可行車底出場路徑。列車i1的可行車底出場路徑有4條，編號為p1～p4，其中，路徑p1為直達路徑，其他為折返路徑，需在途中折返一次，以滿足列車的發車方向。簡便起見，圖2分別僅給出列車i2和i3的最短車底出場路徑p5和p6。注意，車站s6為站前折返站，下行車底進站時直接接入上行正線折返，由此使得列車i3的車底只能在列車i2發車后才能開始辦理接車作業。此外，理論上存在多次折返出場路徑，如路徑p7，采用該路徑的車底需先后在車站s3和s6折返，但通常其空駛距離較長且額外占用折返站能力，實際運營中不予采納。

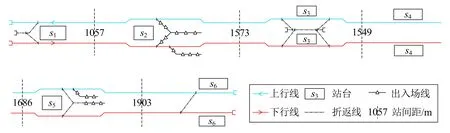
圖1 線路示意

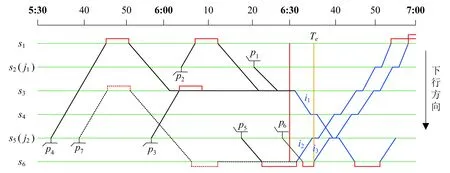
圖2 車底空駛出場示意

車底同時遵循時空可行的路徑和時刻表出場，各條路徑的始發車場、途經車站和折返站存在差異，產生不同空駛距離。直達路徑往往具有較小空駛距離，但受車場檢修及出車能力、車站通過能力、折返站折返能力等限制，直達路徑并非總是可行。同時，車站一般不設置到發線，車底到達所擔當列車始發站后需停留在正線待發，使得后續同方向車底不能通過該車站，部分車底不得不采用折返路徑迂回出場，增加空駛距離。為確保運行安全，必須保證任意兩車底出場時在時空上不存在沖突。受列車發車時刻的影響，在一些出場路徑上，車底不能在運營開始時到達所擔當列車的始發站，如路徑p6，車底不能與運營時段內的列車存在時空沖突。即使采用相同的出場路徑，不同的車場發車時刻將導致車底空駛時間存在差異，例如，路徑p5和p6途經相同車場和車站，但前者在車場發車時刻更早，需要更長的空駛時間。為節約運營成本，在不增加車底總空駛距離的同時應盡量減少總空駛時間。車底空駛出場一般不需要在中間站停車，但因線路能力有限總會產生車站等待時間，在相同的等待時間下可能有許多等價的停站方案，若這些時間隨機分布到沿途中間站，將導致額外起停車作業，增加中間站工作負擔，故實際運營中應盡量減少車底出場在途經中間站的停留時間，讓其快速運行至擔當列車始發站待發。

綜上，本文問題可描述為：給定線路布置及能力，車場布置及能力、折返站布置及能力以及需由運營時段前集中空駛出場的車底擔當的列車等信息，確定所有列車所需車底的配屬車場、出場路徑及時刻表，使得任意列車由適當車底擔當，所有車場檢修及出車能力、所有車站和折返站能力均不違背，任意車底和列車在時空上不沖突，且車底出場總空駛距離和總空駛時間最小，并盡量保證車底在所擔當列車始發站集中待發。

1.2 問題假設

城市軌道交通線路車底全日出入場走行過程可分為3個階段，包括運營時段前集中出場，運營時段內分散出入場和運營時段后集中入場。3個階段相互聯系，共同影響車底運用效率，求解車底全日出入場走行方案的理想策略應是集成3個階段進行協調優化，然而這樣的策略對于具有多車場、多車型和多列車交路的線路研究難度大。鑒于車底在運營時段內分散出入場可視為普通列車，允許載客，不產生空駛，同時在運營時段后集中入場不需要占用車站正線待發，安排難度和空駛距離降低顯著，本文研究第一階段的運營時段前車底集中空駛出場路徑與時刻表綜合編制。為便于后續方法闡述，提出以下假設：

(1)線路運營時段內的列車運行圖和車底交路計劃已完成編制。

(2)不考慮需在沿途折返2次及其以上的復雜車底出場路徑。

(3)為將車場開始上班時間設置在合理水平，引入車場最早允許出車時刻，規定任意車場向兩個方向發出車底的時刻不能早于其最早允許出車時刻。

(4)鑒于城市軌道交通線路車底起停車附加時間較短，同時為增加車底集中空駛出場的靈活性，無論車底是否在中間站停車，規定各區間運行時分均包括起停車附加時間。

2 數學模型

2.1 網絡抽象

將研究的城市軌道交通線路抽象為有向網絡，基于此，提前生成各列需要由車場發出的車底進行擔當的列車的所有可行出場路徑。

以圖1所示線路為例，其抽象網絡如圖3所示。頂點集由三部分構成，包括車站正線頂點1～11，折返線頂點12和13，車場頂點14和15。各車站下行和上行正線一般情況下各設置1個頂點，各折返站根據其配線情況設置頂點。車站s1為單向站后折返站，車站s3為雙向站前折返站，這兩類車站同時設置正線和折返線，接發車和折返允許部分平行作業，前行列車進折返線停穩后可辦理后行列車接車進路，前行列車出清折返線后可辦理后行列車進折返線進路。因此，在車站s1和s3分別設置1個折返線頂點。車站s6為單向站前折返站，在這類車站不設置折返線，下行車底依次接入上行正線辦理折返作業，前行列車需出清車站后才可辦理后行列車接車進路。由此，只為車站s6設置上行正線頂點6，不設置下行正線頂點16和折返線頂點17。現場折返站還存在站后雙折返線折返和站前雙渡線折返等配線設置形式，技術上可交替進行兩列車底的折返，但為避免進路沖突，確保作業安全，現場一般只固定使用其中的1條站后折返線或1條站前單渡線來辦理折返作業。為此，對這兩種類型的復雜折返站，本文參照其對應的簡單折返站(即圖1中的車站s1和s6)在抽象網絡中設置頂點。各車場分別設置1個頂點，可向兩個方向發車。

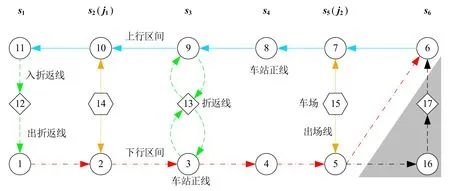
圖3 網絡抽象示意

弧集包含四部分，分別為區間弧、入折返線弧、出折返線弧和出場弧。區間弧表示車底在區間運行，基本位于同方向兩相鄰車站正線頂點間。在折返站s6，下行列車直接接入上行正線折返，車站s5和s6間的下行區間以從車站s5下行正線頂點5到車站s6上行正線頂點6的弧表示。折返線弧表示車底在折返站正線與折返線間的走行過程，在各折返站，折返線弧根據其折返方向進行設置，入折返線弧連接接車正線頂點與折返線頂點，出折返線弧連接折返線頂點與發車正線頂點。折返站s3可辦理兩個方向車底的折返作業，盡管任意方向的車底折返物理上不占用相應的車站正線，但此時該正線不能用于接車，即任意方向的車底折返對同方向車站正線構成間接占用，為此，每個折返方向分別引入1條入折返線弧和1條出折返線弧。出場弧表示車底從車場到銜接車站正線的走行過程，在各車場，出場弧根據其發車方向進行設置，對各發車方向，車場頂點通過1條出場弧連接可達的銜接車站正線頂點。為各弧引入長度和時間屬性，表示車底在該弧對應物理路徑上的走行距離和時間。出場弧的屬性取為車底從車場到銜接車站的走行距離和時間，區間弧的屬性取為區間長度和運行時間，入/出折返線弧的屬性取為車底入線/出線走行距離和時間。

將研究線路基于上述規則抽象為有向網絡后，任意列車所需車底的可行出場路徑等價于抽象網絡中從具備檢修功能車場對應的頂點到該列車始發車站對應正線頂點的路徑。分別生成每列列車的所有可行車底出場路徑，以保證每條出場路徑獨立，對應唯一的列車和途經頂點集合。所有可行出場路徑可在抽象網絡中采用深度優先或廣度優先等搜索算法確定，便于實施，可先忽略可行性生成所有的出場路徑，然后從中刪除途經多個折返站或折返線長度小于車底長度的不可行路徑。前文已述，運營時段內有部分列車始發時刻在線路運營開始時刻之后，但需要運營時段前從車場發出的車底擔當，例如圖2中的列車i3，這些列車的車底需同時與運營時段前的出場車底和運營時段初的載客列車時空不沖突。為此，將研究時段結束時刻從運營開始時刻(圖2中為06：30)推遲為列車的最晚始發時刻(圖2中為Te)。同時，將各列車的可行車底出場路徑拓展為兩部分：一部分在抽象網絡中生成，從該路徑的始發車場對應的頂點到列車始發站對應的正線頂點，稱為可變部分，車底在這部分路徑上途經頂點的到發時刻有待決策；另一部分根據運營時段內的運行圖生成，從該路徑列車始發站對應的正線頂點到研究時段結束時刻列車途經的最后一個車站對應的正線頂點，稱為固定部分，車底在這部分路徑上途經頂點的到發時刻由運行圖給定，是需要滿足的時空約束。

以圖2中的列車i1為例，假設車場j1可對該列車的車底進行檢修，且運營時段內的運行圖規定研究時段結束時刻該列車運行至車站s4，則路徑p1為其可行車底出場路徑，在圖3中表示為(14，2，3，4)，其中頂點14到3的路徑基于圖3的抽象網絡生成，為可變部分，頂點3到4的路徑由運行圖給定，為固定部分。類似地，對于列車i3，假設該列車的車底可在車場j2檢修，且研究時段結束時刻該列車正好在其始發站出發，則其可行車底出場路徑p6在圖3中表示為(15，5，6)，其中可變部分為頂點15到6，固定部分只含頂點6。

2.2 符號說明

為便于模型構建，首先對將使用的集合、參數和變量進行定義，見表1。

表1 集合、參數及變量定義

表1(續)

表1(續)

2.3 目標函數

日常運營中，車底在運營時段前集中出場一般不允許載客運行，需快速運行至所擔當列車始發站。為降低運營成本，提高車底運用效率，應最小化車底出場總空駛距離。同時，在出場路徑確定后，車底出場時刻雖不會增加空駛距離，但對車底空駛時間產生影響。不合理的出場時刻可能使得車底過早出場，在途經車站或所擔當列車始發站等待較長時間，延長相關人員工作時間，增加運營成本，故還需最小化車底總空駛時間。通常縮短總空駛距離能直接減少運營成本，屬于主要目標，模型引入車場最早允許出車時刻可在一定程度上控制車底空駛時間處于合理范圍，故總空駛時間為次要目標。復合目標函數表示為

(1)

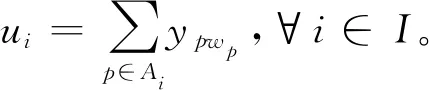
2.4 約束條件2.4.1 路徑唯一性

為保證運營時段初所有考慮列車正常發車，任意列車的車底必須且只能從其候選可行出場路徑集中選擇1條路徑出場，該約束可表示為

(2)

2.4.2 時刻表可行性

各車底在其出場路徑上的各頂點和各弧需分別滿足最小停站時間和走行時間，即

zps′=yps+tss′·xp?p∈P；s∈Sp{op}

(3)

yps-zps≥bps·xp?p∈P；s∈Sp{wp}

(4)

T·xp≤ypwp≤M1·xp?p∈P

(5)

(6)

(7)

式(3)為車底在出場、區間運行、入/出折返線過程中的走行時間應等于規定作業時間標準。式(4)為車底在途經車站正線、折返線的停站時間不小于規定的最小時間，該約束隱含車底在任意頂點的出發時刻不早于相應到達時刻。式(5)左半部分為任意車底在車場的發車時刻不早于該車場規定的最早允許出車時刻，右半部分與式(2)和式(3)共同保證式(1)中車底出場時刻計算的正確性，若路徑p未用于車底出場，其在途經所有頂點s的到發時刻包括在車場的發車時刻均等于0，其中M1取為路徑p對應車場在運營時段內首列車底的出場時刻減去對應出車間隔。式(6)、式(7)為車底在路徑p固定部分途經各頂點的到發時刻等于圖定時刻。

2.4.3 車場檢修能力

城市軌道交通線路的車底一般只有一種，但可配置不同的編組輛數，并在線路上混跑，例如4編/6編混跑，6編/8編混跑等，這里將車底根據其編組輛數進行分類。為確保車底運用安全，現場建立嚴格的車底檢修制度，修程包括列檢、月檢、定修、架修和大修等，規定車底每運營一定時間或里程后需開展相應修程的檢修，其中，車底的列檢和月檢等日常檢修作業通常固定在其配屬車場進行。受場站功能和規模設計的影響，各車場對各類型車底的日常檢修能力是有限的，一般情況下，較短編組的車底可在容納較長編組車底的停車線上駐留并進行日常檢修，反之則不能。因此，在確定車底出場方案時，需滿足配屬于各車場的各類型車底數不能超過該車場對該類型車底的可用檢修能力，可表示為

?j∈J；f∈F

(8)

式中：左半部分表示車場實際配屬的各類型車底數；右半部分表示該車場對該類型車底的可用檢修能力，等于該車場對該車型的總檢修能力減去用于檢修更長車型占用的能力。

2.4.4 車場出車能力

研究線路的車場與其銜接站間通常分別設置1條出場和1條入場聯絡線，運營時段前兩條聯絡線均只供車底出場使用，為避免進路沖突，兩出車方向各占用1條。盡管如此，兩條聯絡線共用同一個咽喉區與車場相連，受場站布置和信號設備的影響，兩相鄰同方向和反方向的車底間都需滿足必要的安全出車間隔。車場在最早允許出車時刻規定下只有有限的出車時段，與出車間隔共同限制其出車能力，該約束可表示為

?j∈J；p，p′∈Bj|p≠p′

(9)

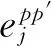
(10)

(11)

?j∈J；p，p′∈Bj|p≠p′

(12)

2.4.5 車站能力

城市軌道交通線路一般采用基于通信的列車控制系統(CBTC)，實現移動自動閉塞行車，基于此車底可以足夠小的距離追蹤運行。然而，車底在車站到發和通過需辦理一系列技術作業，包括辦理進路、進/出站等，兩相鄰同方向的列車在車站需滿足一定的到達和出發間隔，由于列車運行速度是一樣的，不存在區間越行，這里只考慮到達間隔。同樣的，車底在車站折返也存在辦理進路、入/出折返線等技術作業過程，兩相鄰辦理同方向折返的車底間也需滿足必要的到達間隔。由列控系統引起的車站能力約束表示為

?p，p′∈P|p≠p′；s∈Sp∩Sp′且s?J

(13)

式中：M3可取為路徑p和p′所對應列車始發時刻的較大值。此外，研究線路的車站一般不設置到發線，車底在車站到發和通過只能占用正線，同時，車底在車站折返除需占用正線以外，還需占用折返線。各車站的各條正線和折返線同一時間最多只允許1個車底占用，要求途經同一條車站正線或折返線的兩相鄰車底應滿足必要的發到間隔，即

?p，p′∈P|p≠p′；s∈Sp∩Sp′且s?J

(14)

s∈Sp∩Sp′且s?J

(15)

s∈Sp∩Sp′且s?J

(16)

?p，p′∈P|p≠p′；s∈Sp∩Sp′且s?J

(17)

2.5 兩階段算法

綜上，車底空駛出場路徑與時刻表綜合優化問題可構建為

M式(1)

s.t.式(2)～式(17)

簡單的車底空駛出場路徑問題可約簡為具有頂點約束的多商品網絡流問題，后者已被證明為NP-hard問題[8]，由此原問題本質上是NP-hard的。然而，模型M為混合整數線性規劃模型，利用主流商業優化軟件(CPLEX，GUROBI等)即可快速獲得中小規模問題的最優解。通常研究線路的車場和折返站數量較少，且運營時段初需要從車場發出車底進行擔當的列車數量也不多，使得所有可行車底出場路徑的條數有限，原問題的規模是可控的。同時，線路上的非車場銜接站、非折返站和非列車始發站對車底出場方案無實質影響，提前約簡這部分車站不會漏掉最優出場路徑，并可進一步減小原問題規模。此外，原問題為戰術層面決策，對模型求解無實時性要求，在合理時間內求得最優解即可。因此，借助于所提出的線性模型M，本文直接采用商業優化軟件求解原問題。

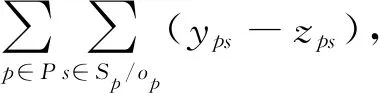
3 案例分析

以某城市軌道交通線網中最繁忙線路實際數據為例，驗證所提出方法的有效性。采用MATLAB 2015b編程所提出優化方法，并調用CPLEX 12.6求解其中的優化模型。所有計算在CPU為Inter Core i5-4590 3.3 GHz，內存為16 GB的64位個人電腦上執行。

3.1 案例描述

測試線路全長54 km，設車站39座，如圖4所示，2015年日均客流量達69.8萬乘次，全年客流量超2.5億乘次。全線分別在車站s3和s28附近設置車場j1和j2，車場信息見表2，其中前者只可檢修6編組車底，后者可檢修6編組和8編組車底。全線沿線共設置8個折返站，折返站信息見表3，所有折返站均為單向折返，其中可將車底從上行折返為下行的折返站3個，將車底從下行折返為上行的折返站5個，目前日常運輸組織中啟用6個折返站，剩下2個備用。車站s11和車站s32設有渡線，可在特殊情況下分別發揮上行和下行折返站作用。折返站s28為車場銜接站，運營時段前只用于車底出場，不辦理車底折返。

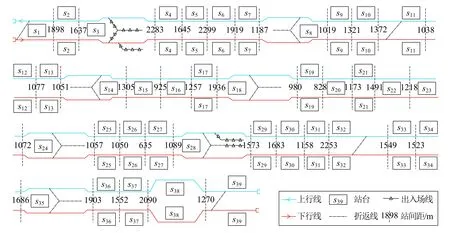
圖4 測試線路

表2 車場信息

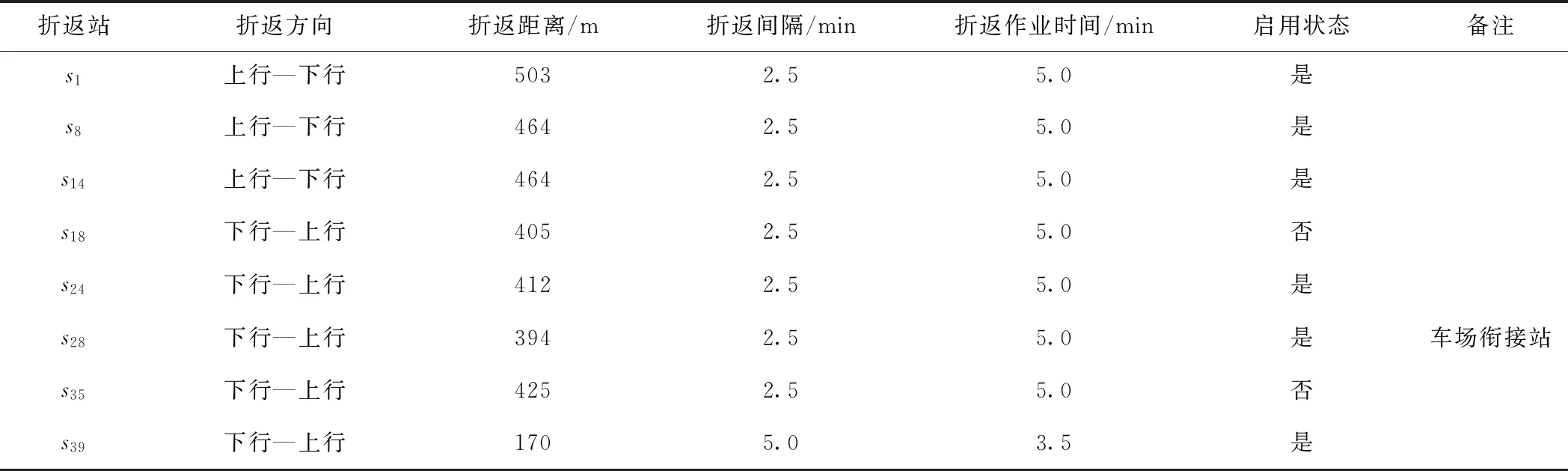
表3 折返站信息

測試線路06：30開始運營，選擇該線路某工作日的分號列車運行圖進行案例分析。運行圖里共有31列列車(編號為1～31)需由運營時段前從車場始發的車底擔當，車底出場路徑與時刻表有待確定。同時，由問題定義研究時段結束時刻Te取為最晚的列車4的始發時刻06：43：55，在線路運營開始時刻與研究時段結束時刻間，還有5列列車(編號為32～36)直接從車場始發，這些列車在車場的發車時刻及其至研究時段結束時刻的運行路徑和途經車站的到發時刻由運行圖給定，是在安排前31列列車車底出場方案時需遵守的時空約束。

對于測試案例，現行基于經驗編制的車底出場方案如圖5所示，結合現場習慣，不展示車底在車場發車和在折返線作業的過程及到發時刻，同時，簡便起見，忽略研究時段結束時刻之后不屬于研究范疇的運行線。現行車底出場方案的統計信息見表4，其中，第1列為列車編號，第2～4列分別為列車始發站、始發方向及始發時刻，第5列為擔當車底在車場的發車時刻，第6列為空駛距離，注意，后續計算結果只對前31列列車進行統計和分析。設兩車場最早允許出車時刻為05：00，已知車站到達間隔和發到間隔分別為2.5 min和1.5 min，編號為20、26和31的列車需要8編組車底，其余列車需要6編組車底。

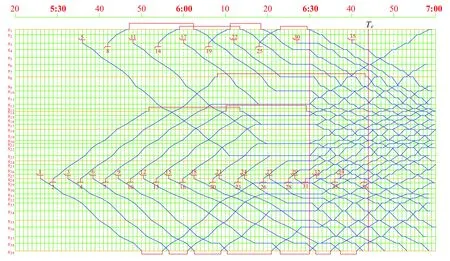
圖5 現行車底出場方案

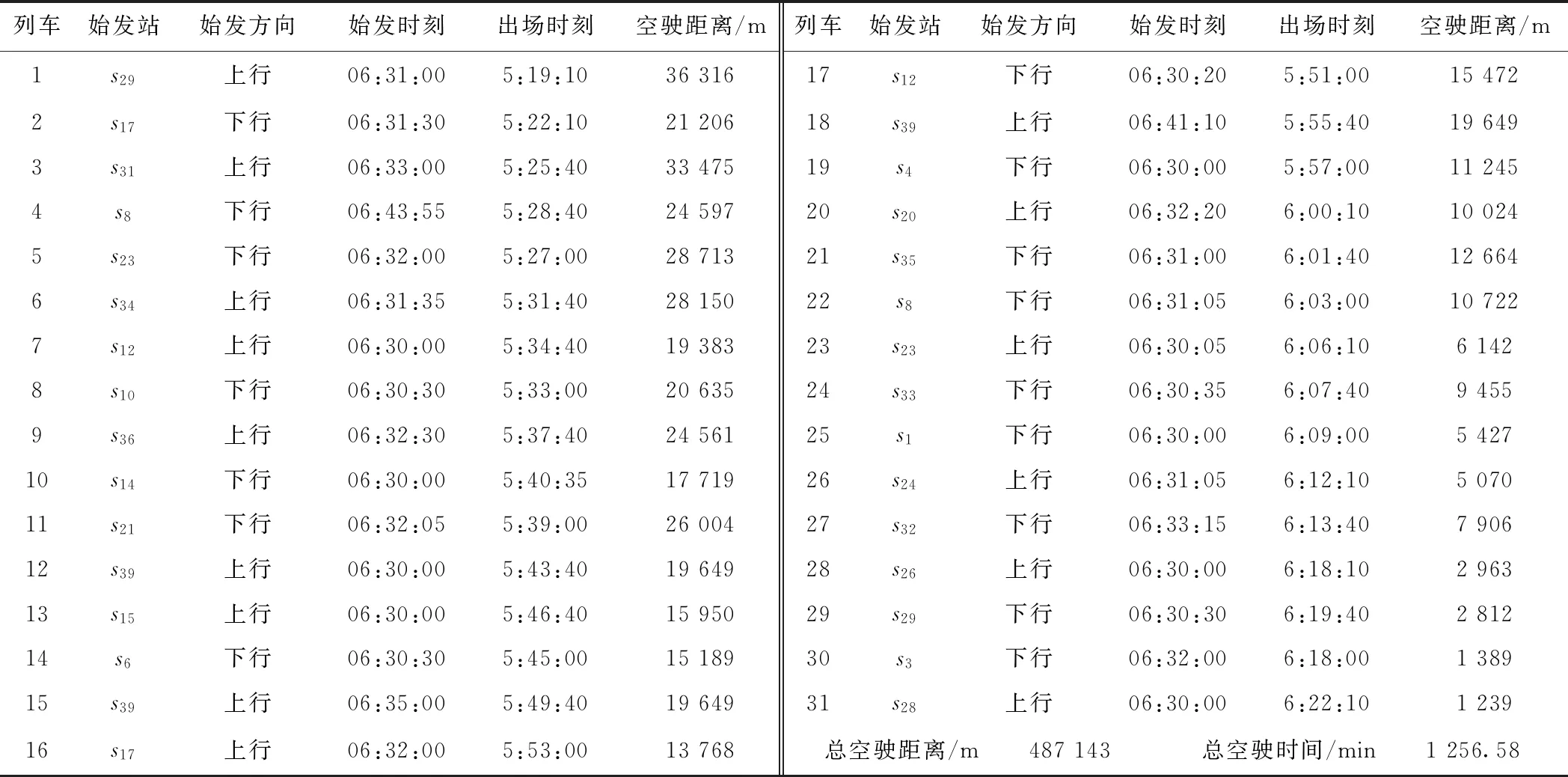
表4 現行車底出場方案的統計

由圖5和表4可知，由經驗方法編制的車底出場方案中，車場j1和j2分別辦理9列和22列車底出場作業，其中，共14列車底采用折返路徑出場，17列車底采用直達路徑出場。車底總空駛距離為487 143 m，總空駛時間為1 256.58 min，車場發出首列車底出車時刻為5：19：10。因車場出車能力及車站能力限制，列車4需由配屬于車場j2的車底采用折返路徑出場擔當，產生較長空駛距離和空駛時間。

3.2 計算結果

使用兩階段算法求解測試案例，尋找高質量的車底出場方案，共生成車底出場路徑173條，從中剔除不合理路徑后，剩余可行出場路徑110條。所提出算法共耗時1 607 s收斂，其中第一和第二階段分別耗時1 604 s和3 s。優化車底出場方案如圖6所示，相應的統計信息見表5，簡便起見，表5僅給出前31列列車的車底出場方案。

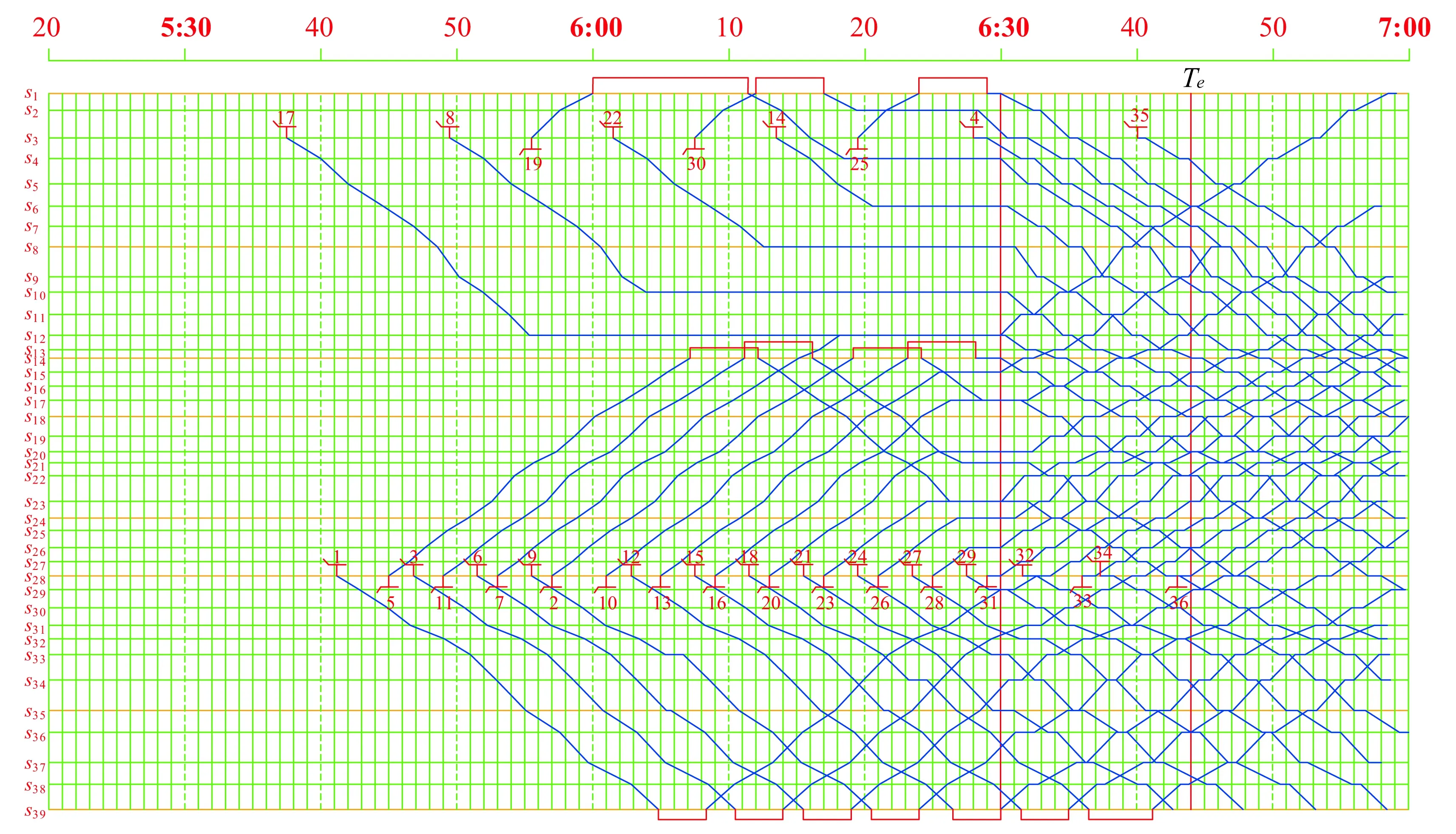
圖6 優化車底出場方案

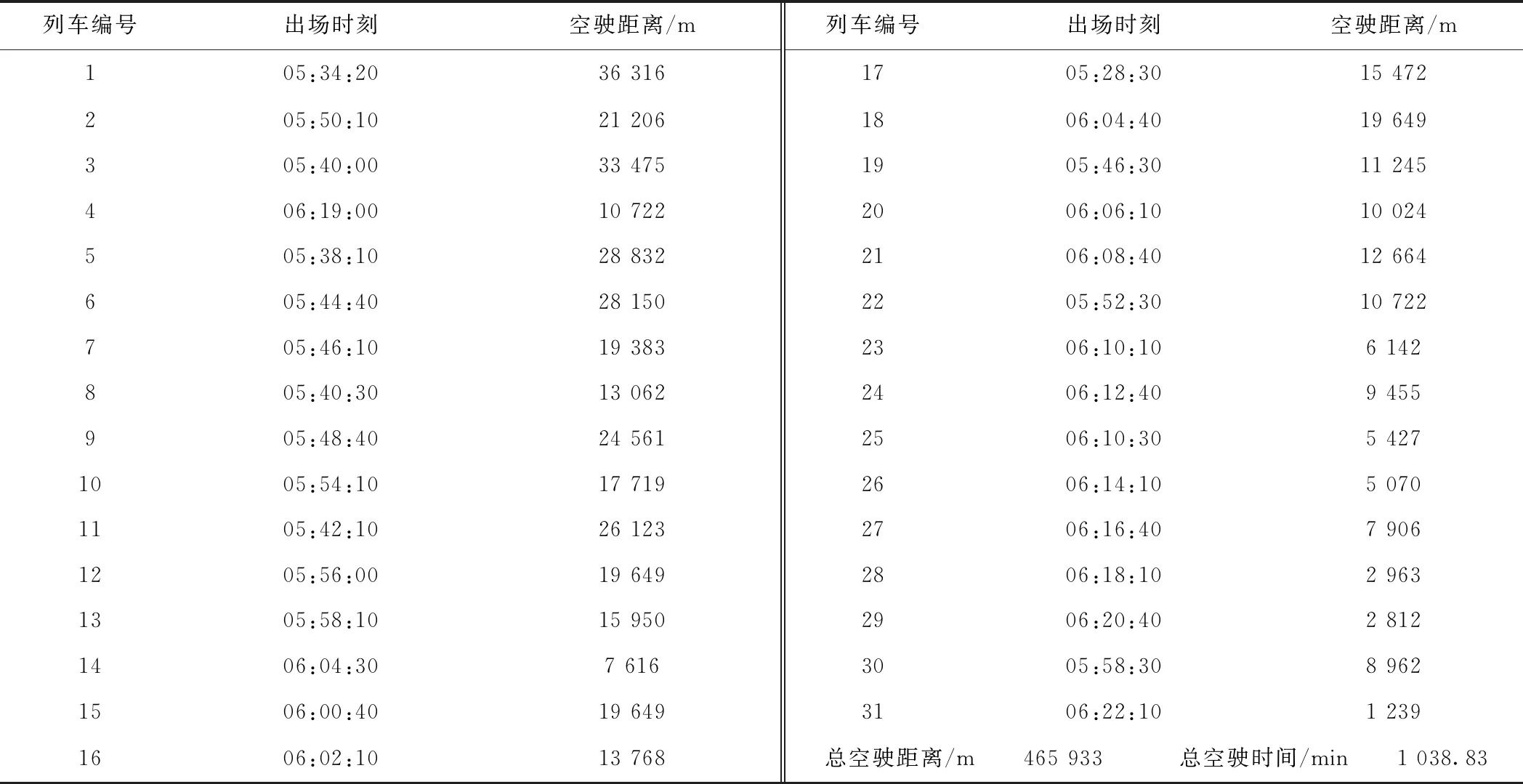
表5 優化車底出場方案的統計

由圖6和表5可知，從統計結果來看，優化后，車場j1共辦理8列車底出場作業，車場j2共辦理23列車底出場作業，其中，共14列車底采用折返路徑出場，17列車底采用直達路徑出場。車底總空駛距離為465 933 m，總空駛時間為1 038.83 min，車場開始辦理車底出車作業的時刻為5：28：30。相比于現行方案，優化出場方案中每日車底總空駛距離縮短21 210 m，縮短率為4.35%，預計全年空駛距離節省量將超過7 700 km，同時，車底總空駛時間節省217.75 min，節省率為17.33%，車場可推遲9.33 min開始辦理出車作業。

車底出場路徑方面，與現行方案比較，優化方案在所有列車中僅對列車4、5、8、11、14和30的車底出場路徑進行了調整。列車4、8和14的車底出場路徑由原來的折返路徑調整為直達路徑，共縮短空駛距離29 021 m。列車4的車底出場路徑由原始發于車場j2的折返路徑調整為始發于車場j1的直達路徑，空駛距離縮短13 875 m，占總空駛距離縮短量的65.4%，效果顯著。列車8和14的車底出場路徑由原始發于車場j1的折返路徑調整為始發于相同車場的直達路徑，空駛距離均縮短7 573 m。列車5、11和30的車底出場路徑由原來的直達路徑調整為折返路徑，共增加空駛距離7 811 m。列車30的車底出場路徑由原始發于車場j1的直達路徑調整為始發于相同車場的折返路徑，空駛距離增加7 573 m，變化明顯，但好處在于使得列車4可由更近車場j1的車底采用直達路徑進行擔當，縮短了總空駛距離。列車5和11原由始發于車場j1的車底通過直達路徑進行擔當，但空駛距離均較長，盡管優化方案將這兩列列車的車底出場路徑都調整為始發于車場j2的折返路徑，但代價較小，空駛距離均只增加119 m。

從計算時間來看，第一階段模型的求解占據絕大多數時間，給定第一階段的最優解，第二階段的輔助模型可極快求解。雖然所提出算法求解時間稍長，但原問題為戰術層面非實時決策問題，算法求解時間處于合理范圍。因此，所提出優化方法能在合理時間內獲得實際可行的車底出場方案，具有優良的求解效果，優于目前現場經驗方法，可用于輔助現場提高城市軌道交通線路運營時段前車底出場方案的質量，從而減輕工作負擔，節約運營成本。

3.3 靈敏度分析

測試案例兩個車場的出車間隔有較大不同，使得這兩個車場可發出的車底數存在較大差異，由此可能導致部分列車因車場出車能力不足需由較遠車場的車底進行擔當，增加總空駛距離和總空駛時間。此外，案例中有2個折返站未啟用，可能使得部分車底需去較遠的折返站辦理折返。現采用靈敏度分析方法探討可能進一步縮短總空駛距離和總空駛時間的措施，分別為通過技術改造縮短車場出車間隔和啟用備用折返站。

3.3.1 縮短車場出車間隔

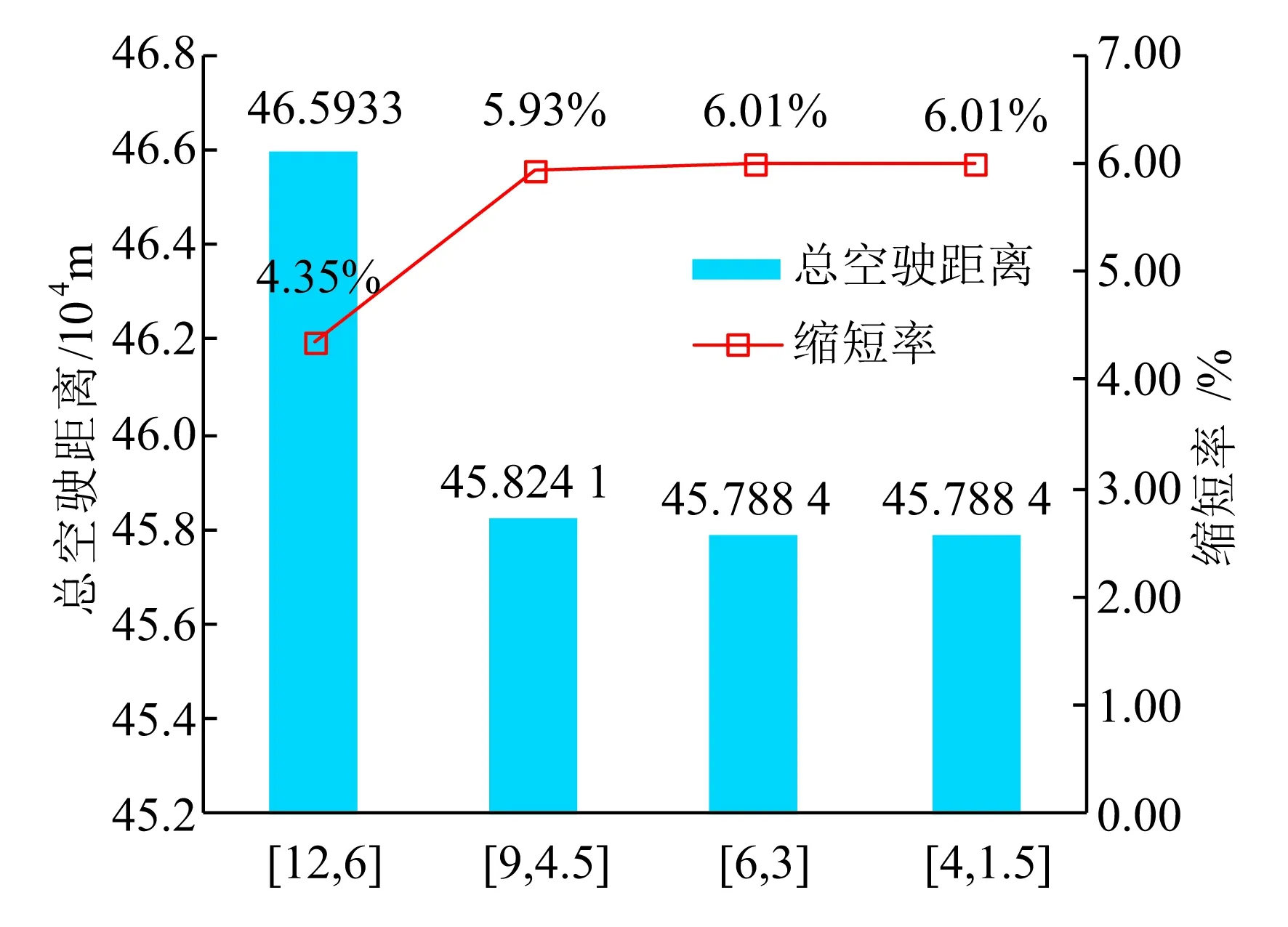
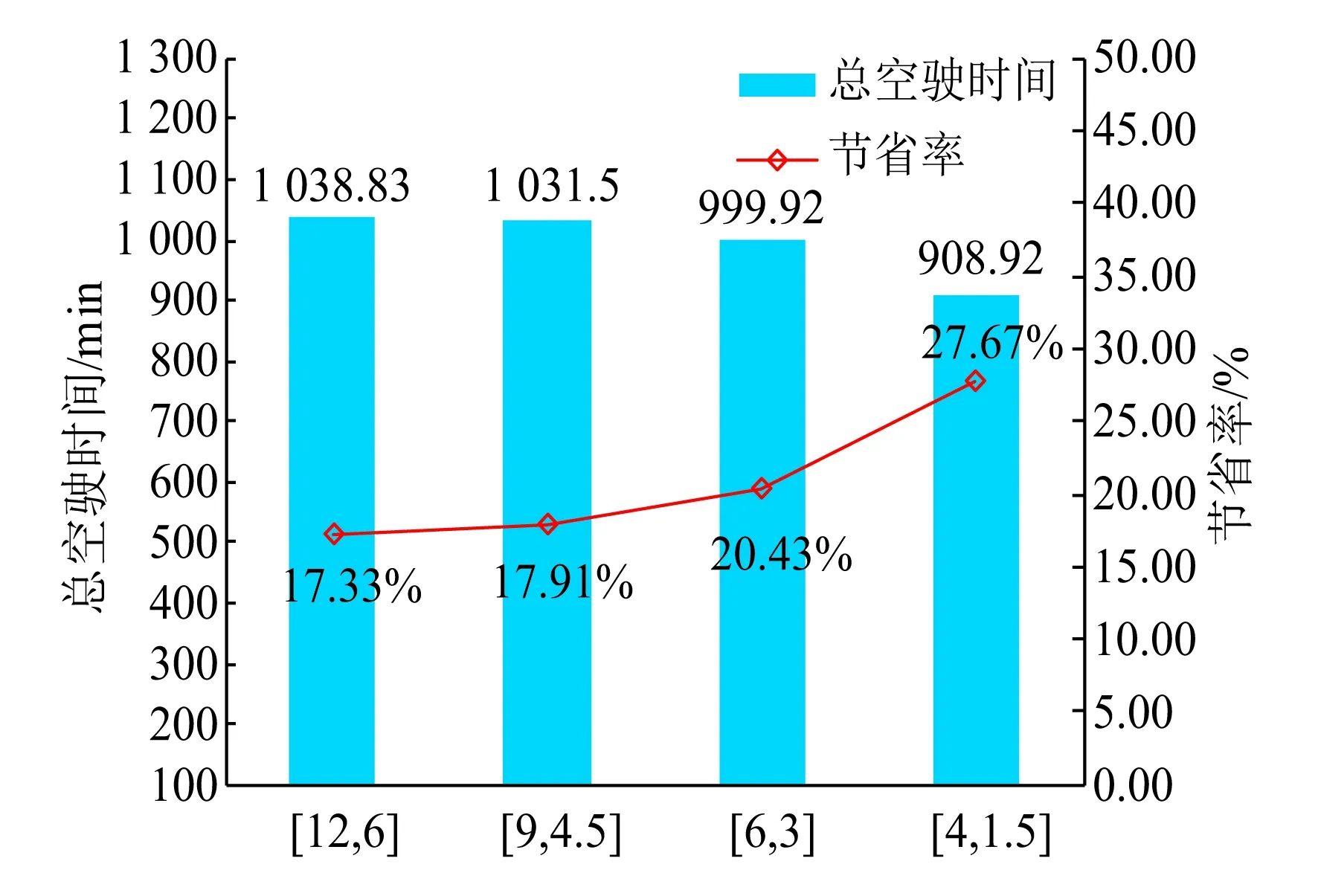
首先探討車場出車間隔對車底總空駛距離和總空駛時間的影響。測試案例中車場j2的出車間隔小，理論上已難以進一步壓縮，因此，考慮只縮短車場j1的出車間隔，同時固定車場j2的出車間隔。根據測試線路信號部門的反饋意見，車場j1的出車間隔共設計以下四種情況：同向12 min，反向6 min；同向9 min，反向4.5 min；同向6 min，反向3 min；同向4 min，反向1.5 min。對于各種情況，保持其他參數設置不變，依次求解優化模型，結果如圖7所示，其中，[12，6]表示同向和反向出車間隔分別為12 min和6 min的情況，縮短率和節省率分別表示總空駛距離和總空駛時間相對經驗方案的改進比例。

(a)總空駛距離

(b)總空駛時間

由圖7可知，隨著車場出車間隔的減少，該車場出車能力逐漸增大，更多始發站在附近的列車可由該車場的車底擔當，從而可縮短總空駛距離和總空駛時間。當出車間隔由[12，6]縮短為[9，4.5]時，總空駛距離縮短率增量較為顯著，由4.35%增加為5.93%，總空駛時間節省率增量較為平緩。當出車間隔由[6，3]進一步縮短為[4，1.5]時，總空駛距離縮短率維持不變，而總空駛時間節省率增量較為明顯，由20.43%增長為27.67%。所有情況中兩個車場的檢修能力均存在富余。可得出結論，車場出車能力對車底總空駛距離和總空駛時間具有較大影響，在一定范圍內縮短車場出車間隔能減少總空駛距離和總空駛時間。

車場出車間隔由車場的線路布置、信號條件及行車組織方法等因素決定，縮短車場出車間隔可采用許多技術改造和技術組織措施，不同的措施具有特有的技術條件要求、工程投資和適應性，建議相關部門在設計車場出車間隔縮短方案時，先對候選方案進行技術經濟綜合比選，評估各候選方案的技術可行性、所需工程投資、以及縮短總空駛距離和總空駛時間所獲得的運營節省，再從中選擇合理的方案。

3.3.2 啟用備用折返站

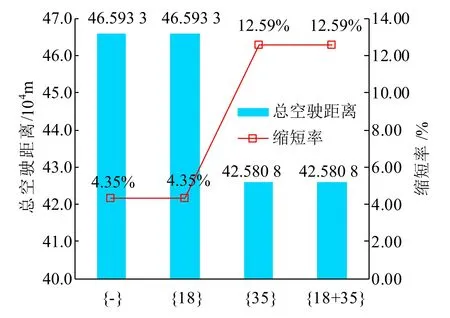
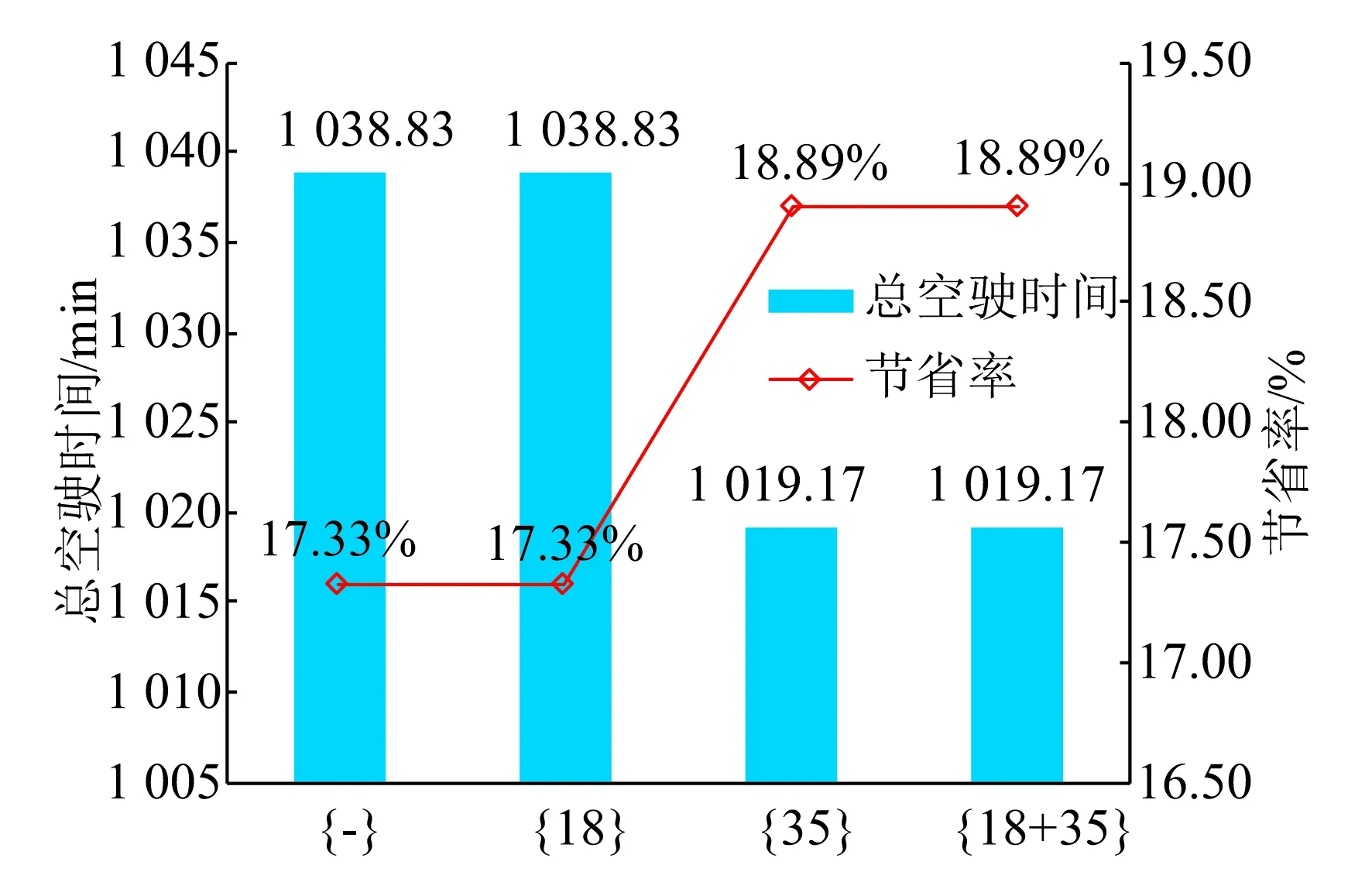
現探討啟用備用折返站對車底出場方案的影響。測試線路有兩個備用折返站s18和s35，均可將下行方向車底折返為上行。分析以下4種情況：不啟用備用折返站；啟用車站s18；啟用車站s35；啟用車站s18和s35。對于各種情況，不改變其他參數，求解優化模型，結果如圖8所示，其中，{-}表示未啟用備用折返站，{s18}表示啟用折返站s18。

(a)總空駛距離

(b)總空駛時間

由圖8可以看出，單獨啟用折返站s35可在優化方案基礎上進一步縮短總空駛距離和總空駛時間，且對前者的優化效果更為顯著，其增量達到8.24%。單獨啟用折返站s18不能進一步縮短總空駛距離和總空駛時間，盡管同時啟用兩個備用折返站可進一步提高出場方案質量，但其優化效果是由開通折返站s35所獲得的。由此可判斷，單獨啟用折返站s35能進一步改善運營時段前車底出場方案，考慮到開通備用折返站可能存在技術改造和費用支出，建議相關部門在進行技術經濟比選后考慮是否啟用部分備用折返站。

4 結束語

本文提出城市軌道交通線路運營時段前車底空駛出場路徑與時刻表綜合優化方法。通過提前生成所有可行車底出場路徑，以車底出場總空駛距離和總空駛時間最小為目標，滿足若干運營和能力要求，構建混合整數線性規劃模型。設計兩階段算法，以最小化車底在途總停站時間為目標，對所得最優解進行二次優化，盡量減少車底在途不必要的起停車作業，以提高獲得車底出場方案的實際可操作性。實際案例分析結果表明，所提出優化方法可在合理時間內獲得比現場經驗方法更優的車底出場方案，可用于輔助實際決策。若技術經濟條件允許，適當提高瓶頸車場出車能力或者啟用備用折返站可進一步提高車底出場方案的質量。

本文致力于對運營時段前車底空駛出場路徑與時刻表進行綜合優化，所提出模型對于大規模實際案例需要花費相對較長的時間，未來有必要研究更有效的優化算法，以進一步加快尋找高質量車底出場方案的效率。其次，論文研究宏觀的車底空駛出場路徑與時刻表問題，以正線和折返線集計表達車站級的基礎設施，下一步可以軌道電路為單元更為細致地建模車站的基礎設施，進而研究微觀的車底出場路徑與時刻表綜合優化方法。此外，勾畫完整的車底交路計劃需協調安排車底在運營時段前集中出場、運營時段內分散出入場和運營時段后集中入場3個走行過程，運營時段內考慮車底分散出入場走行的車底交路計劃問題以及集成全日車底出入場走行的車底交路計劃問題也是將來研究的方向。