基于核密度估計的鐵路橋梁構件地震易損性分析

單德山，張二華，董 俊，李 喬

(西南交通大學 土木工程學院，四川 成都 610031)

地震概率風險評價方法已成為評價地震風險的最常用方法，目前已在世界范圍內得到應用[1-3]。地震概率風險評價方法研究的關鍵是地震危險性分析、構件和子結構及系統的地震易損性評估[1]。文獻[1]在系統總結橋梁易損性分析方法基礎上，將橋梁結構常用地震易損性分析方法歸納為分析型、經驗型、專家意見型和試驗型四類。近年來，分析型易損性分析方法主要依據結構的地震數值分析結果建立地震易損性曲線，幾乎不需要做大量實際震害統計調查工作，因此受到國內外學者的廣泛關注[1]。

橋梁地震易損性曲線反映了橋梁結構在給定地震動強度參數下達到一定破壞狀態的概率，在交通運輸網地震風險評估中具有重要作用[1-4]，而有效的概率密度函數估計方法是計算橋梁地震易損性的核心。文獻[5]將現有概率密度函數估計方法分為參數和非參數兩類。在此基礎上，文獻[6]將橋梁結構地震易損性分析方法劃分為參數和非參數兩類。而目前較常采用的MLE(Maximum Likelihood Estimation)法[1，7]和PSDA(Probabilistic Seismic Demand Analysis)法[1，8]均基于某種人為假定(如對數正態分布假定)，分別通過概率統計和線性回歸確定條件概率密度函數估計中的未知參數，從而建立易損性曲線。然而，文獻[4，9-10]均指出上述方法在解決復雜柔性結構的地震易損性問題時，計算結果可能與實際震害不符。

目前非參數化的地震易損性方法主要基于蒙特卡羅模擬(Monte Carlo Simulation，MCS)[1，11-12]。MCS法基于概率統計基本含義，通過對大量橋梁地震計算樣本進行統計獲得橋梁構件的易損程度，但該方法的計算結果精度極易受到計算樣本量的影響[5，12]，若要獲得較為可靠的結果，則需大量的計算。該方法因耗時嚴重而難以推廣使用[12]。

綜上所述，上述三種常見分析型地震易損性分析方法均難以適應日趨復雜的橋梁結構抗震性能評估，為此，本文引入一種非參數的核密度估計KDE方法用于地震易損概率密度函數的估計，建立一種非參數化的橋梁結構地震易損性分析方法，并通過對比分析由MLE、PSDA、MCS和KDE計算獲得的橋梁結構易損概率，驗證KDE方法的準確性，采用Bootstrap重抽樣方法驗證KDE方法的精度。在此基礎上，用所提方法計算某鐵路剛構-連續組合體系橋梁的易損性曲線，分析不同構件的易損排序，為橋梁結構的抗震設計提供依據。

1 橋梁地震易損性的KDE估計

1.1 基本思路

由概率統計[5]問題出發，橋梁地震易損性分析屬于條件概率估計問題[1，12]，用fD|IM表示橋梁構件抗震能力的條件概率密度函數，易損性函數Pf(IM，C)可表示為[9，12]

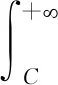
(1)

式中：D、C為橋梁構件抗震需求和抗震能力；IM為峰值加速度取a時的地震動激勵強度指標；fD|IM(C)為結構抗震能力C的條件概率密度函數，根據條件概率密度函數與聯合概率密度函數的關系[5，12]，fD|IM(C)可寫為

(2)

式中：fD，IM(·) 為數組(D，IM)的聯合概率密度函數；fIM(·)為IM的邊緣概率密度函數[5]。獲得fD，IM(·)、fIM(·)后，可通過式(1)獲得橋梁構件易損性曲線。

基于分析型地震易損性方法的基本思路[1]，首先通過計算得到橋梁構件在不同IMi(i=1，2，…，n)地震激勵下的Di(i=1，2，…，n)值，n為選用的地震動數量，然后構建樣本對{Di，IMi}(i=1，2，…，n)，最后將KDE方法用于估計聯合概率密度函數fD，IM(·)與邊緣概率密度函數fIM(·)。

1.2 易損性KDE估計

采用KDE方法從隨機變量X的有效樣本{x1，x2，…，xn}中估計得到概率密度分布函數[13]

(3)

(4)

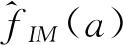
(5)

當給定獨立同步隨機變量時，對于多維隨機向量X∈Rd，其核密度估計可表示為[5，13]

(6)

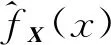
(7)

可通過插件法或交叉驗證方法估計H[13]，求解多維隨機向量X的帶寬矩陣H。求解不確定隨機變量間的相關性問題時，其核密度估計可通過采用完全型帶寬矩陣[14]求解，在本文所建立的方法中，采用交叉驗證法中最穩定的平滑交叉驗證方法[15]來估計H。

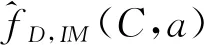
(8)

將式(8)、式(5)代入式(2)，得到fD|IM(C)后，對式(1)積分形成最終結構易損性函數

Pf(IM，C)=P[D≥C|IM]=

(9)

需要注意的是，式(9)中hIM和H的選取，對橋梁結構地震易損性分析結果的準確性具有關鍵作用[5，12，14-15]。

1.3 易損性KDE估計的統計特性

采用KDE方法得到結構地震易損性曲線的同時，可通過計算所得易損性曲線的置信水平，評判計算結果的正確性和易損性分析方法的穩定性。Bootstrap重采樣法無需額外信息[16]，基于原始樣本對對樣本觀測信息進行復制，從概率統計角度實現總體分布特性的推斷估計，本文沿用此方法對KDE易損性分析方法的統計特性進行討論。

首先有放回地從原始{Di，IMi}(i=1，2，…，n)樣本對中抽樣，各數據被抽中的概率均為1/n，經m次重復抽樣獲得m個Bootstrap樣本[16]，進而采用本文方法，獲得各Bootstrap樣本的易損概率，在此基礎上，獲得與建立結構易損性曲線相關的概率統計指標，如中位數、置信區間、方差等[5，12，16]。

1.4 橋梁結構地震易損性KDE估計流程

體系復雜的橋梁結構，其抗震能力受到本身材料、幾何參數以及外部地震動激勵等諸多不確定因素的影響[1-4，12]。考慮上述不確定因素，基于IDA(Incremental Dynamic Analysis)[17]方法，本文采用的研究思路如圖 1所示。由圖1可知，本文通過對比參數化PSDA、MLE方法及非參數化MCS、KDE方法對相同橋梁結構地震易損性的計算結果，驗證本文所提KDE方法的正確性和可靠性。在此基礎上，對橋梁結構易損構件的地震損傷概率進行KDE估計，根據構件易損性排序，為橋梁結構抗震設計提供依據。

圖1 橋梁地震易損性分析流程

2 橋梁結構地震易損性分析

2.1 工程概況

本節以我國西部某4跨高墩剛構-連續組合體系橋梁為例，對本文所建立的KDE地震易損性分析方法進行驗證和應用，其跨徑布置為(68+2×120+68+3×32+24) m，如圖2所示。其場地反應譜特征周期為0.35 s。主梁為二次拋物線形式的變截面C55混凝土箱梁，跨中梁高5.2 m，0號塊處梁高9.0 m。二期恒載為120 kN/m；1～4號墩的基本情況見表1。0號臺和4號墩頂布置縱向活動球形鋼支座，支座型號為QZ9000DX/Z±150/R0.05[18]；1號墩頂布置縱向活動球形鋼支座，支座型號為QZ55000DX/Z±100/R0.05[18]，其設計摩擦系數為0.05，非滑移方向的水平承載力取支座豎向設計承載力的15%。該橋處于9度地震烈度區。

2.2 有限元模型

圖2所示鐵路橋梁主橋的有限元模型采用OpenSees軟件[19]建立。基于橋梁實際震害統計，采用彈性梁單元模擬主梁[1-4，7，9]；依據文獻[20]，采用附加質點模擬二期恒載等其他附加質量對主梁的作用。分別采用彈塑性纖維梁柱單元、理想彈塑性連接單元、接觸單元、零長度單元模擬橋墩、球形鋼支座、伸縮縫以及橋臺與主梁間的相互作用；群樁效應采用6個等效彈簧模擬。該主橋的有限元模型示意如圖3所示。

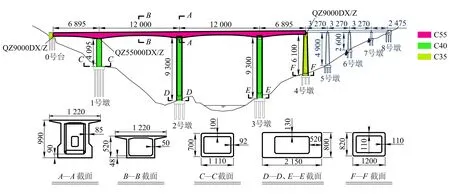
圖2 某鐵路剛構-連續組合橋梁(單位：cm)

表1 1～4號墩基本情況

圖3 橋梁結構有限元計算模型示意

2.3 地震動的選擇

本文所依據工程為西部地區橋梁，為使地震易損性分析結果符合該地區實際[21]，在綜合考慮地震動強度、地震動記錄完整性、設計地震反應譜等因素[22]的基礎上，從“5·12”汶川地震的46個地震臺站中選取100組實測地震動[23]作為激勵，構建本文地震動樣本庫，該樣本庫的詳細信息參見文獻[22]。圖4為所選地震動的加速度反應譜。由圖4可以看出，所選地震動的頻譜特性與該橋場地反應譜特征周期基本一致。

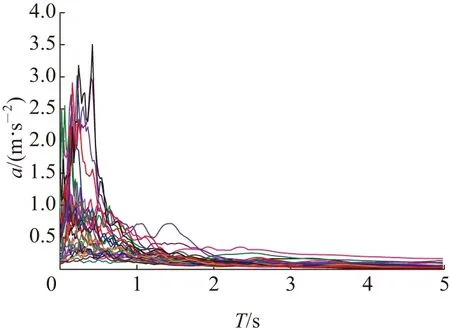
圖4 汶川地震動加速度反應譜

2.4 結構參數不確定性

基于既有結構在參數不確定性方面的研究成果[24]，在考慮鐵路剛構-連續組合橋梁結構特點的基礎上，本文考慮不確定性的結構參數取值見表2。表2中，P1和P2為與分布類型相關的參數，當分布類型不同時，P1和P2含義不同，具體可參考文獻[25]。

表2 結構參數分布類型及分布特征值

2.5 KDE結構地震易損性對比驗證

根據既有橋梁實際震害統計資料[26]和理論分析[25]可知，本文橋梁容易發生損傷的位置主要有：1號墩和4號墩墩底截面、2號墩和3號墩的墩頂和墩底截面以及0號臺、1號墩和4號墩墩頂支座。基于四種地震易損性分析方法(PSDA、MLE、MCS[1]、KDE)，分別構建上述橋梁構件的地震易損性曲線。采用IDA進行構件地震易損性分析過程中，PGA調幅范圍為0.1g～1.0g，增量為0.1g，100條地震動記錄調幅后共獲得1 000條隨機地震波樣本；同時為考慮結構參數的不確定性，采用拉丁超立方抽樣構建1 000個橋梁FEM模型樣本，各橋梁樣本的結構參數按表2所示分布類型隨機生成；將1 000條地震動與1 000個橋梁模型樣本隨機配對后，進行非線性時程分析。

本文分別將曲率延性比和相對位移延性比作為橋墩和支座的地震損傷指標[27]，進行結構地震易損性分析，各構件縱向易損性量化指標見表3，其橫向量化指標可參考文獻[25]，不再列出。

本文在采用MCS法[5，12，16]時，進行了大量計算，獲得了充分的樣本。因此，在下文的對比分析中，將MCS所得結果作為真實結果。

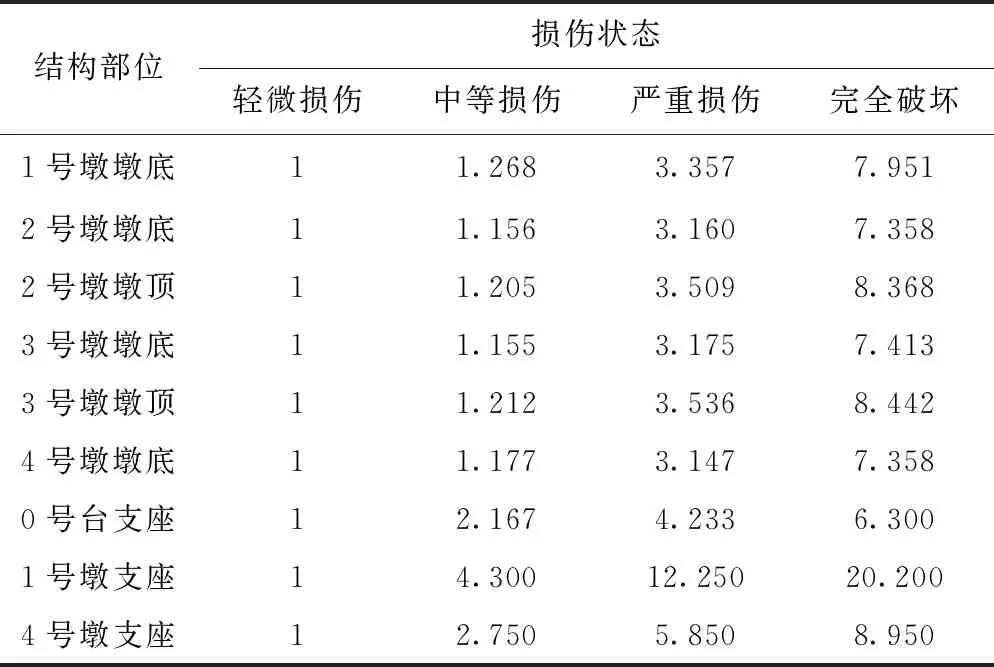
表3 橋梁構件損傷指標

2.5.1 橋墩截面對比分析

以PGA為地震動強度指標，結構地震易損性的損傷程度包括輕微、中等、嚴重和完全破壞四種狀態，對比四種方法分析結果，同一截面共得到16條易損性曲線，若均繪于同一圖中，將不易分辨，本文分別將輕微和嚴重損傷的易損性曲線繪于同一圖中，中等和完全破壞的易損性曲線繪于另一圖中，圖5為2號墩底和墩頂截面、4號墩底截面的縱向地震易損性曲線。

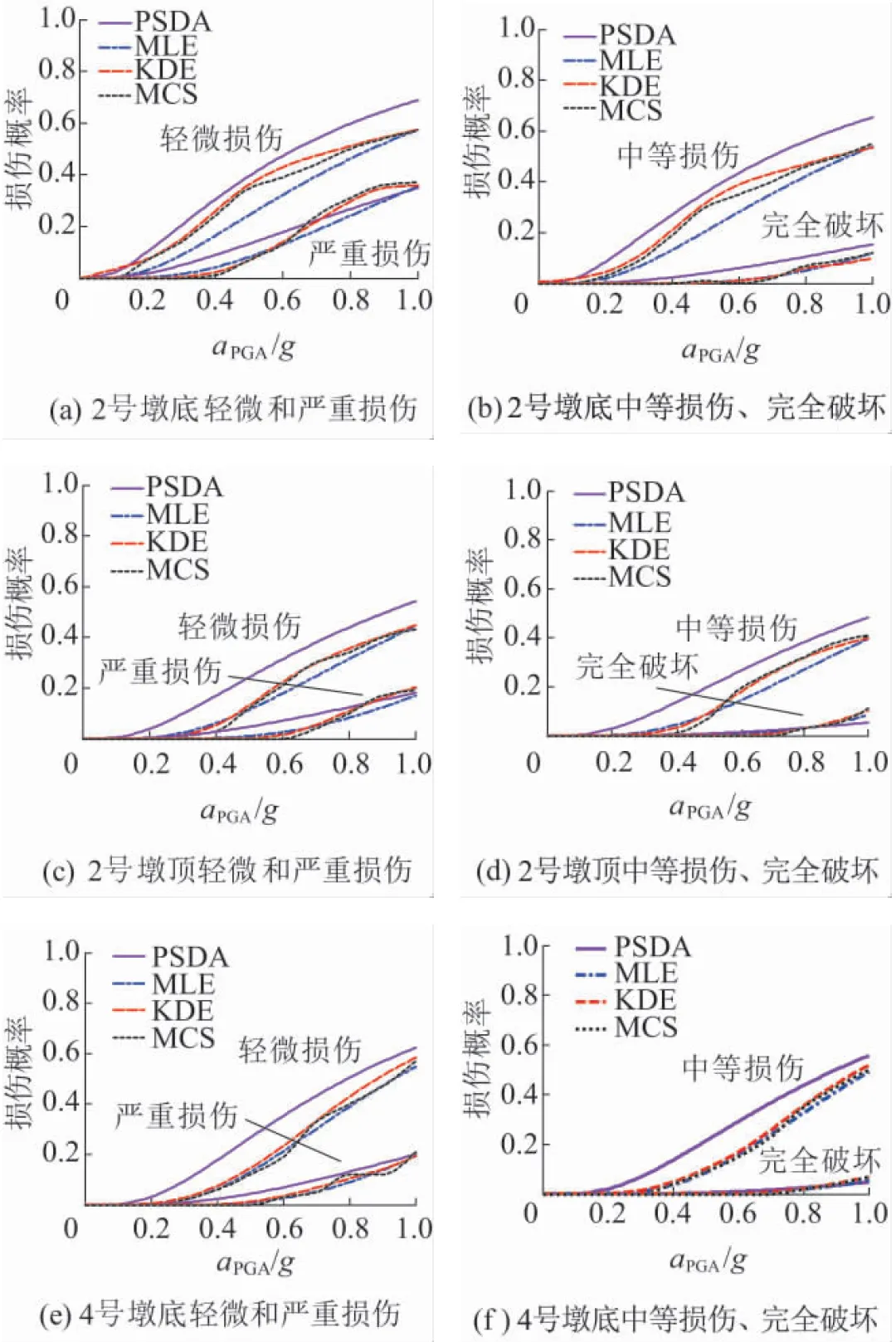
圖5 2號墩底、墩頂和4號墩底截面縱向地震易損性曲線

由圖5(a)和圖5(b)可知，四種方法所得的2號墩底截面易損性曲線存在差異。各損傷狀態下，KDE和MCS兩種非參數方法所得易損性曲線規律一致，相同PGA對應的損傷概率也較接近，即四種曲線中，KDE易損性曲線與MCS易損性曲線更接近。四種損傷狀態下，MLE易損性曲線低于KDE和MCS易損性曲線，即低估了2號墩底截面的損傷概率；而PSDA易損性曲線則高于MCS結果，即高估了2號墩底截面的損傷概率。另外PSDA結果明顯高于其他三種方法的結果。

由圖5(c)～圖5(f)可知，采用KDE和MCS法時，2號墩頂和4號墩底截面易損程度幾乎相同，而基于MLE和PSDA法的易損概率存在較大偏差。MLE結果更接近非參數估計結果，當aPGA>0.5g時，MLE所得損傷概率略低于非參數法得到的損傷概率。PSDA法估計獲得的橋梁易損傷程度大于非參數KDE和MCS法，即PSDA方法所得2號墩頂和4號墩底截面易損程度偏高。

2.5.2 支座對比分析

與橋墩對比分析過程相同，將縱向地震動作用下四種方法的分析結果繪于同一圖中以便對比，0號臺和1號墩頂支座地震易損性曲線如圖6所示。由圖6可知，由兩種非參數法所得0號臺和1號墩頂支座的地震易損性曲線較為一致，而兩種參數估計法所得結果具有一定差異，MLE法與非參數方法估計輕微和中等損傷概率基本一致，嚴重損傷和完全破壞差異較大；而PSDA法僅能較準確估計中等損傷概率，其他三種損傷狀態時，PSDA法與其他三種方法的結果存在較大差異。

圖6 0號臺和1號墩頂支座縱向地震易損性曲線匯總圖

上文僅討論了縱向地震易損性的對比情況，在橫向地震作用下，橋梁構件易損計算結果規律與之相同，不再贅述。

在縱、橫向地震動激勵下，由PSDA和MLE兩種參數估計方法所得橋梁構件地震易損性結果均存在偏差，其原因為：

(1)PSDA和MLE方法均基于前述假定，由上文所述可知，不同橋梁構件的損傷概率并非完全滿足該假定[4，9-10]，特別是高階模態參與較明顯的剛構墩。

(2)易損性函數的參數估計過程中采用的算法亦可導致最終結果出現不同程度偏差，如PSDA方法采用線性需求模型進行參數估計[1-4]。

(3)地震動強度的變化會引起線性回歸參數隨之變化，而地震易損性分析過程則假定線性回歸參數不變。但從總體結果進行分析，MLE法優于PSDA法。

綜上所述，本文所提非參數化的KDE地震易損性分析方法與基于概率統計的MCS方法所得地震易損性結果基本相同，驗證了KDE方法的正確性。

2.6 KDE方法計算結構地震易損性的可靠性驗證

本節以0號臺支座為例，基于2.4節所述基本流程，采用KDE和MCS方法得到橋梁構件地震易損結果的中位數及95%置信水平變化規律曲線，如圖7所示，圖中虛線表示置信區間。由圖7可知，兩種方法計算獲得的地震易損性中位數曲線基本一致。另外，兩種方法所得中位數、地震易損性曲線的置信區間寬度及置信區間變化規律基本相同，從而驗證了KDE方法用于橋梁地震易損性分析的可行性和可靠性。

圖7 0號臺支座易損性中位數曲線及其置信區間

由2.5節、2.6節的對比分析和可靠性驗證可知，本文所提橋梁結構地震易損性的KDE估計，在計算精度上與MCS所得結果一致，但計算效率遠高于MCS法。

用本文所提KDE方法計算圖2所示鐵路橋梁各地震損傷危險截面在縱、橫向地震作用下的易損性曲線，如圖8、圖9所示。

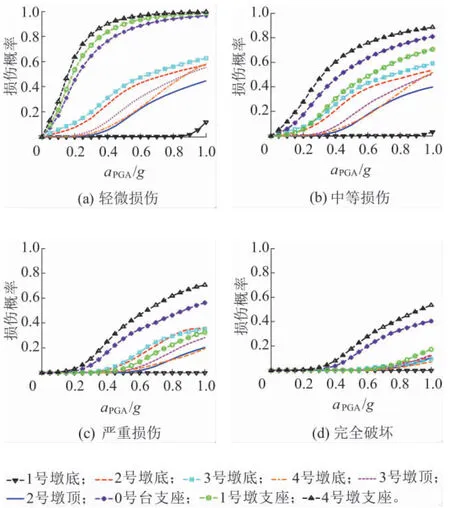
圖8 各危險構件縱向地震易損性曲線

圖9 各危險構件橫向地震易損性曲線

由圖8可知，在縱向地震作用下，4號墩支座最易損傷，其次為0號臺支座。四種損傷狀態下，4號墩支座和0號臺支座的損傷概率均遠高于其他構件。所有危險構件中，1號墩底的損傷概率最低。

設防烈度9度時，各墩底截面發生輕微、中等和嚴重損傷的概率分別小于30%、25%和3%，而完全破壞的概率幾乎為0；各剛構墩頂截面出現輕微和中等損傷的概率均小于15%和8%，嚴重和完全損傷的概率幾乎為0；即9度設防時，橋墩各構件具有良好的縱向抗震性能。

9度設防時，各支座輕微損傷、中等損傷概率分別大于75%和30%，嚴重損傷、完全破壞的概率則分別低于22%和5%，即設防烈度下，各支座構件易發生輕微和中等損傷，但嚴重損傷和完全破壞的概率依然較低，這表明該橋不會因支座相對位移過大而發生落梁震害。

由圖9可知，橫向地震作用下，0號臺支座出現輕微損傷和中等損傷的概率最大，4號墩支座最易出現嚴重損傷和完全破壞，而1號墩底截面最不易出現地震損傷。

9度設防時，各墩底截面發生輕微、中等和嚴重損傷的概率分別低于20%、13%和2%，完全破壞的概率幾乎為0，即設防烈度下，各橋墩構件的橫向抗震能力良好。設防烈度(9度)下，各支座構件輕微、中等和嚴重損傷的概率分別低于50%、20%和5%，且幾乎不會出現完全破壞的情況，即9度設防時，各支座易出現輕微損傷，但中等及以上損傷的概率較低，這表明支座的橫向抗震性能良好。

在相同強度橫向地震作用下，各支座損傷概率明顯小于縱向地震的損傷概率，這是因為支座縱向設計水平力、橫向設計水平力分別為豎向設計承載力的5%和15%，即與縱向水平承載力相比，其橫向水平承載力更大，進而使得橫向地震位移較小，易損程度較低；而橋墩承受的橫向水平荷載比支座處增加，其橫向地震損傷概率增大(如1號墩、4號墩)。

2.7 各危險部位易損性對比分析

采用超越概率地震動強度指標中位數描述各構件易損性[4，9]，比較各構件易損性的具體情況，某損傷狀態下地震動強度的中位數越小，構件越易出現地震損傷。本文各構件的PGA中位數如圖10所示。

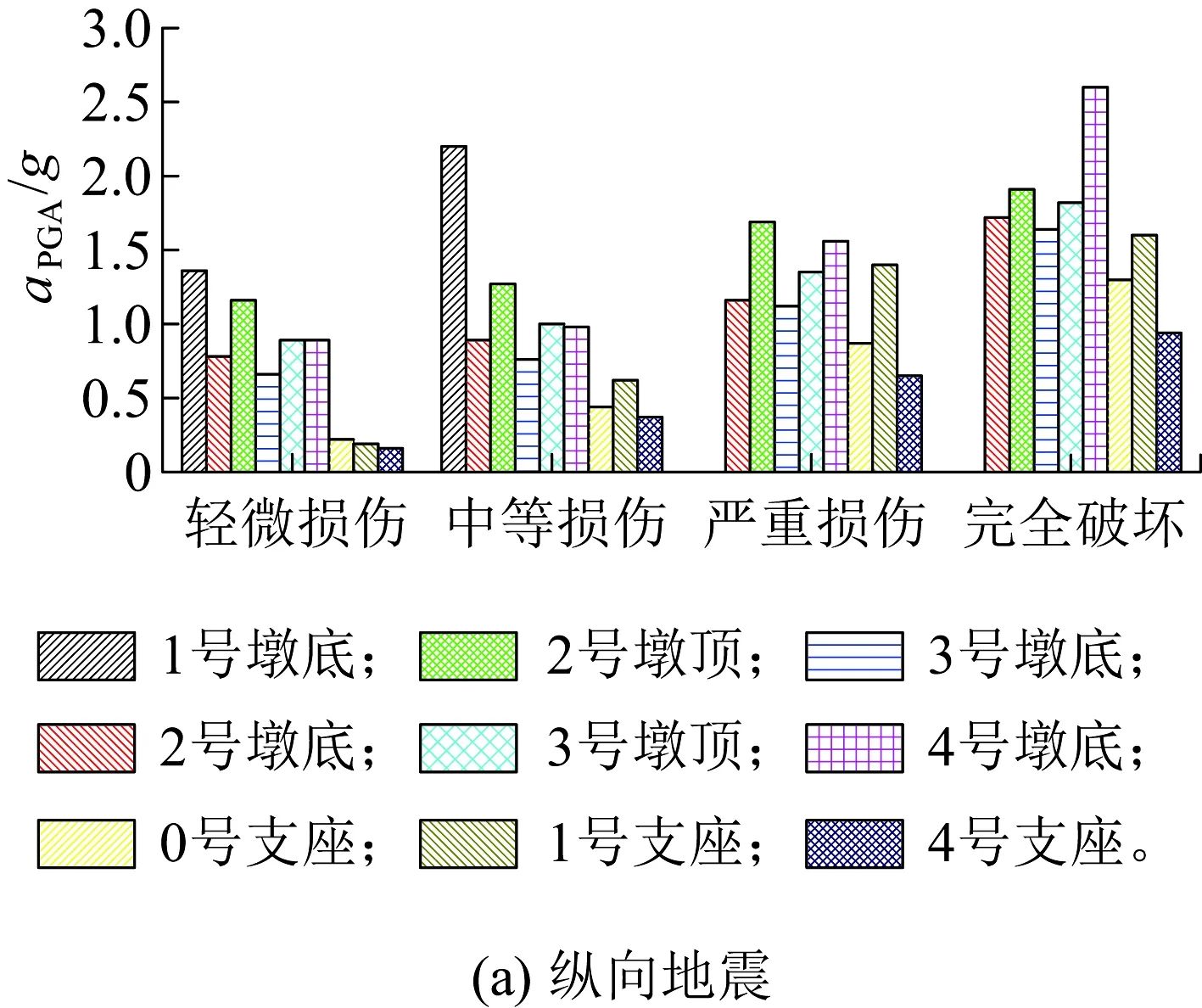
圖10 各危險構件PGA中位數柱狀圖

由圖10(a)可知，縱向地震作用下，1號墩底、4號墩底、3號墩頂、2號墩頂4個部位的輕微損傷和中等損傷的易損排序與嚴重損傷和完全破壞的排序存在較大差異。分析認為，該橋墩高相差較大，各墩幾何尺寸、配筋和混凝土強度等級不同，屬于典型的非規則結構體系，這使得各墩的抗震性能出現差異，不同損傷狀態表現出不同的易損順序。因此，實際橋梁工程中，應重視非規則橋梁的抗震設計。

由圖10(b)可知，橫向地震作用時，4號墩和0號臺支座最易出現損傷，但1號墩支座的易損排序與縱向地震易損排序差異較大。由2.1節中的支座型號和布置情況可知，1號墩頂支座橫向抗震設防能力大于4號墩和0號臺支座，其對應損傷指標自然大于4號和0號支座。另外，4號墩和0號臺為主梁提供端部支撐，而1號墩則為主梁提供中間連續支撐，從抗震需求上也需較大的橫向抗震能力。

3 結論

針對現有橋梁結構地震易損性分析方法的不足，本文提出結構地震易損性分析的核密度估計方法，驗證了所提方法的正確性和可靠性，并用所提方法實現了橋梁結構的地震易損性分析，結論如下：

(1)經對比和可靠性驗證，本文結構地震易損性核密度估計方法所得結果的統計特征與蒙特卡洛模擬(MCS)的結果基本一致。

(2)通過兩類易損性分析方法對比，基于人為假定的參數化方法所得易損性分析結果的精度受地震激勵、橋梁類型、概率密度估計算法影響嚴重。本文非參數化方法中，MLE方法優于PSDA方法。

(3)設計地震作用下(9度設防)，算例橋梁各墩的抗震性能良好。相同地震強度下，剛構墩的損傷概率大于懸臂墩。

(4)設計地震作用下(9度設防)，各支座易出現輕微和中等損傷，但嚴重和完全破壞的概率幾乎為0。此外，支座比橋墩更易損傷，即支座為最易損部位。