含運動副間隙的渦旋壓縮機驅動軸承動力學仿真分析

趙 嫚，張 強，閆鵬舉

（蘭州理工大學石油化工學院，甘肅蘭州730050）

1 引言

“節能降耗”是中國可持續發展的基本國策，渦旋壓縮機作為一種新型容積式壓縮機械，具有經久耐用、節能高效等優點，已被廣泛應用于制冷與空調、各種氣體壓縮、增壓泵等領域[1]。

轉子系統良好的動力學特性是保障渦旋壓縮機高效、可靠運行的關鍵[2]。從結構及承載方面的綜合考慮，渦旋壓縮機曲柄銷與動渦盤輪轂處多采用滾針軸承聯接。實際生產中轉子系統構件的加工誤差、裝配誤差以及磨損會導致轉子系統的運動副產生大小不同的間隙；壓縮機在運行過程中動渦盤受氣體傾覆力矩的作用，使軸承隨其發生傾斜，從而加劇了軸承的沖擊碰撞及過摩擦損耗，導致轉子系統機構動力學特性惡化[3]，因此對含運動副間隙渦旋壓縮機動渦盤傾覆特性下，驅動軸承的動力學特性研究具有重要的工程應用價值。

國內外學者對含運動副間隙渦旋壓縮機的動力學展開了多年的研究，并取得了一定的成果。文獻 [4]基于虛擬樣機技術對渦旋壓縮機轉子系統進行了動力學特性及有限元研究，施加氣體力研究曲柄銷與驅動軸承之間的單個間隙對壓縮機動力學特性的影響，但其僅采用5個主軸轉角下的氣體力計算結果模擬壓縮腔氣體力變化，且未考慮動渦盤與防自轉機構之間的間隙以及軸承與曲柄銷之間不同間隙值大小的影響；文獻 [5]針對小軸防自轉機構渦旋壓縮機進行了動平衡仿真，研究運動副間隙對渦旋壓縮機動平衡的影響，但未考慮氣體力作用下動渦盤傾覆所帶來的影響。

本文基于虛擬樣機技術以某臥式渦旋壓縮機轉子系統為研究對象，建立起含運動副間隙的渦旋壓縮機轉子系統動力學模型，根據計算結果在ADAMS軟件添加氣體力進行仿真，分析動渦盤傾覆下不同運動副間隙對驅動軸承動力學參數變化規律的影響，并根據仿真結果得出動盤傾覆下軸承的偏磨區域，為渦旋壓縮機的優化提供了重要的理論參考。

2 渦旋壓縮機轉子系統的結構

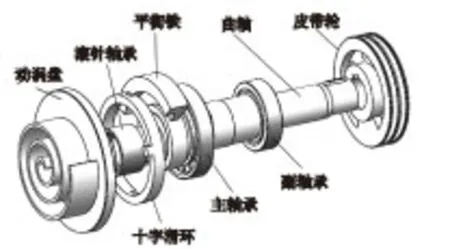
圖1 渦旋壓縮機轉子系統的結構

不同類型渦旋壓縮機的轉子機構會有一定差異，但大致結構組成相同。本文采用的某臥式渦旋壓縮機轉子系統如圖1所示，主要由動渦盤、滾針軸承、十字滑環、大小平衡鐵、曲軸等零件組成。當皮帶輪帶動曲軸旋轉時，動渦盤在曲柄銷的驅動下以及十字滑環防自轉機構的限制下，相對靜渦盤作公轉平動使得壓縮腔容積發生變化，完成壓縮機的吸氣、壓縮和排氣[6]。

3 含運動副間隙轉子系統動力學建模

3.1 運動副間隙的矢量模型

首先應對運動副間隙進行正確的描述，本文引入一個間隙矢量eij來描述含間隙轉動副中軸承和曲柄銷的相對運動關系，即軸承和曲柄銷之間連接點的相對位置可通過間隙矢量來表示，如圖2所示，OXY為慣性坐標系。模型中間隙矢量的變化可以反映出動渦盤傾覆時，軸承與曲柄銷之間是否發生接觸[7]。

矢量模型中間隙大小可以用軸承內圈半徑與曲柄銷半徑之差描述，則間隙為

式中rj——軸承內圈的半徑

ri——曲柄銷的半徑

3.2 運動副間隙的接觸碰撞力模型

國內外學者對含間隙機構動力學進行了廣泛的研究并建立了許多運動模型，相比其他模型，二狀態運動模型的仿真結果更貼近實驗結果，這里采用二狀態運動模型。

二狀態運動模型中的非線性彈簧阻尼模型常應用于旋轉鉸的描述，這里選用該模型建立軸承與曲柄銷的間隙接觸碰撞模型，如圖3所示，其廣義形式可表示為

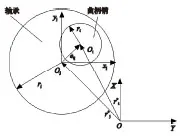
圖2 運動副間隙矢量模型示意圖

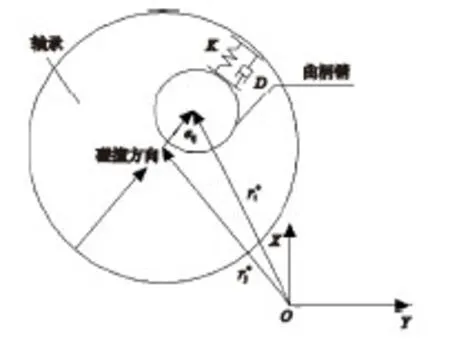
圖3 非線性彈簧阻尼模型

式中Fn——法向接觸力

Fk——彈簧恢復力

Fd——等效阻尼力

Kn——等效接觸剛度

δ——法向穿透深度

δ˙——為法向相對速度

C（δ）——與δ有關的阻尼因子

m——指數，且m≥1

多體動力學軟件ADAMS中Impact函數模型采用非線性彈簧阻尼器模型計算碰撞接觸力。Impact函數的接觸力計算公式為

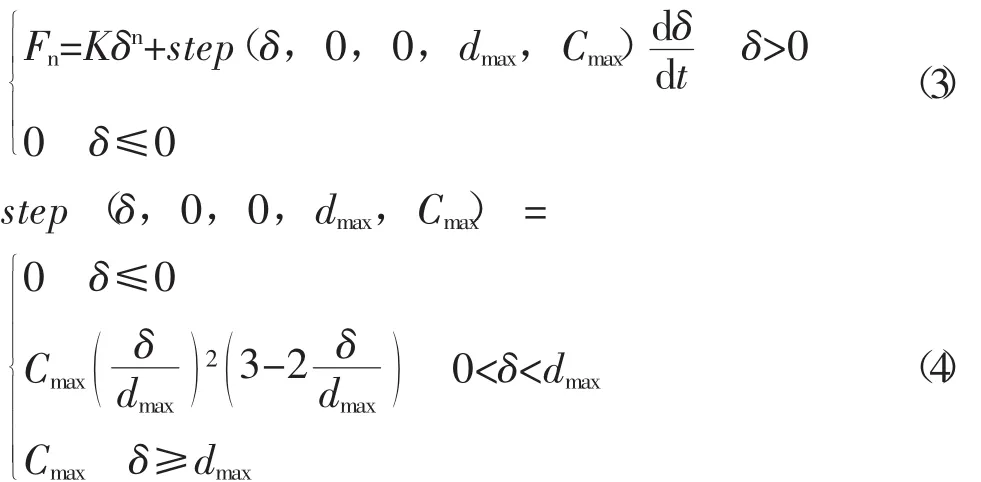
式中K——接觸剛度系數

δ——兩構件之間的穿透深度

dδ/dt——構件的相對碰撞速度

n——≥1的力指數

Cmax——最大阻尼系數

dmax——使用Cmax計算出來的穿透邊界的的深度

3.3 運動副間隙的摩擦力模型

這里選用修正的庫倫摩擦力模型描述間隙鉸處的摩擦力，其較為廣泛地應用于碰撞模型的摩擦行為中，切向摩擦力計算公式為

式中 μd——鉸接處滑動摩擦系數

cd——動態修正系數

υt——兩構件的相對切向速度含間隙運動副處的軸承與曲柄銷發生碰撞時，產生了接觸碰撞力，該約束力可定義為Fc，并根據碰撞過程加入階躍函數

則間隙處的約束力為

當軸承與曲柄銷發生接觸時，含運動副間隙轉子系統的動力學方程為

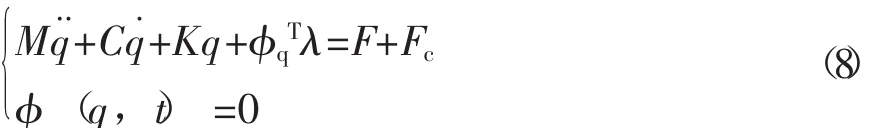
式中q——轉子系統的廣義坐標列陣

M——廣義質量陣

C——廣義阻尼陣

K——廣義為剛度陣

φq——約束方程的雅克比矩陣

F——廣義速度二次項以及力陣

λ——拉格朗日乘子

t——時間

4 含運動副間隙轉子系統仿真模型的建立

4.1 轉子系統三維實體模型的建立

ADAMS軟件建模能力相對較弱，這里選用SolidWorks軟件建立轉子系統的實體模型。建立模型時應盡可能簡單，以減少建模過程和轉配過程中的工作量，比如去掉螺栓、油道、開孔等。樣機干涉檢查合格后，裝配好的樣機以x_t格式進行保存。該轉子系統已通過理論平衡配平，達到動、靜平衡，動渦盤質心理論上處于滾針軸承中心軸線上。滾針軸承與曲柄銷連接處為含間隙的轉動副，動渦盤與十字滑環配合處為含間隙的點線副。

4.2 轉子系統動力學模型的建立

保存好的模型導入ADAMS中，根據模型設置恰當的單位、重力以及柵格大小，對機構中的每一個構件分別進行顏色設置、重命名、材料屬性定義，各構件參數如表1所示。

根據轉子系統實際工作情況對各構件施加驅動、約束和測量，其中理想旋轉副采用轉動副進行定義，含間隙的運動副采用接觸副（Contact）進行定義。仿真時建立一個剛體圓環等效替代靜渦盤，它起到限位作用，ADAMS/view里ground相當于機架體，轉子系統各部件之間的約束關系見表2。

由動渦盤的受力分析可知，壓縮機運行過程當中動渦盤會受到傾覆力作用，使滾針軸承隨動渦盤出現傾斜趨勢。根據計算結果，在動渦盤1/2齒高的基圓半徑處添加氣體傾覆力，使其動渦盤產生實際工況下的傾覆效果。在ADAMS中根據SPLINE函數定義單向力，并根據計算結果設置其大小和方向，其中力函數公式中的SPLINE樣條擬合曲線根據氣體力變化規律建立且隨曲軸轉角變化而變化，在SPLINE擬合方法對話框中選擇Cubic Fitting Method選項[9]。

忽略壓縮機啟動階段，設置皮帶輪轉速為2900 r/min，仿真步數定為5000步，仿真時間為0.1s。樣機建模完成后進行自檢以達到仿真要求[10]。參數設置完成后的轉子系統虛擬樣機模型如圖4所示。

分析過程中所有部件假設均為剛體，為了保證滾針軸承模型在動力學分析中部件的幾何結構不失真，避免發生零件接觸穿透，在零件接觸時采用Solid to Solid的接觸形式。在接觸卡片設置時采用Impact接觸函數的算法，參數設置如表3所示。

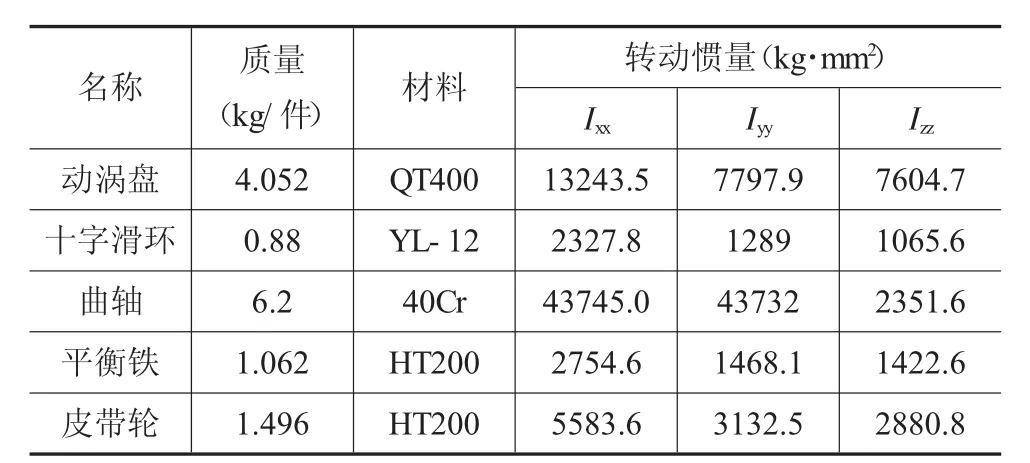
表1 主要運動部件相關參數

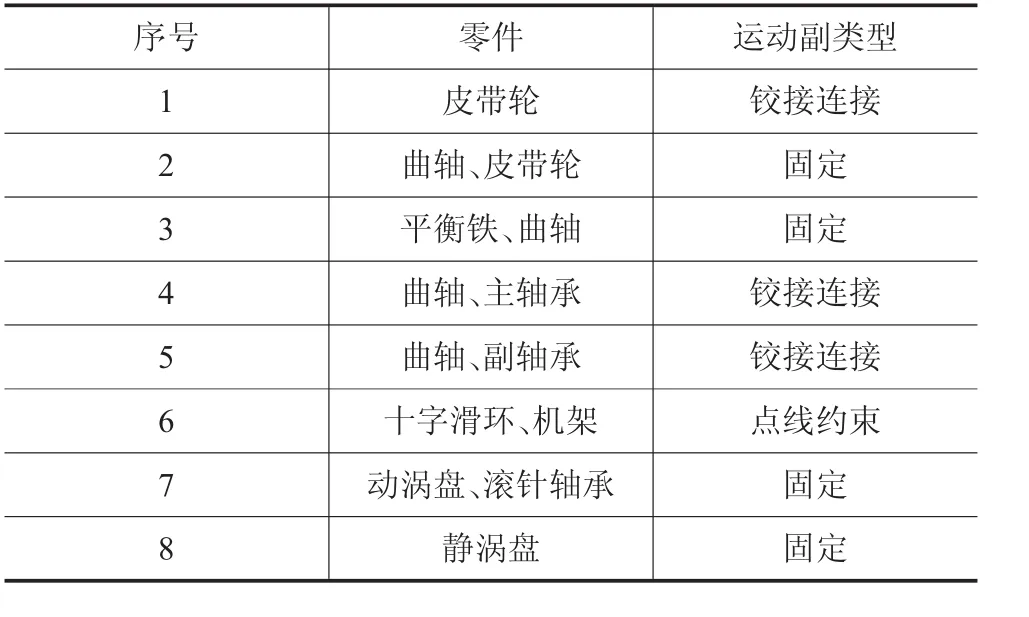
表2 各部件之間的約束關系

5 動力學仿真結果與分析

根據曲軸機構加工等級，曲柄銷公差范圍為0.01～0.05 mm，則最終選取間隙值為0 mm（理想約束）、0.01 mm、0.03 mm、0.05 mm進行仿真和分析。十字滑環與動渦盤配合鍵槽處間隙取最大公差0.09 mm，動渦盤和十字滑環Contact接觸，十字滑環另一側凸鍵與機架體為理想點線約束。主軸承、副軸承與主軸鉸接不含間隙。氣體力隨曲軸旋轉發生周期性變化，仿真結果選擇一個周期進行分析，圖5所示為滾針軸承運動參數，圖6所示為運動副接觸碰撞力，圖7所示為滾針軸承質心軌跡。

由圖5（a） 可知，理想模型與含間隙模型中的滾針軸承位移曲線幾乎重合，這表明動渦盤傾覆下間隙對滾針軸承的位移幾乎沒有影響。圖5（b） 與圖5（d） 可知，間隙的存在使得軸承的速度與角速度相對理想狀態出現小的波動，間隙值越大，速度波動峰值越大，間隙值0.05 mm模型的速度最大峰值相對理想狀態下偏差約為4.85%，但速度曲線整體的趨勢相同，所以間隙對滾針軸承的速度與角速度的影響也比較小。但由圖5（c）與圖5（e） 可知，理想模型滾針軸承的加速度和角加速度曲線很光滑，但含間隙模型的加速度與角加速度出現脈沖式波動且瞬時峰值很大，當間隙尺寸增加到0.05 mm時，加速度曲線相比理想模型出現明顯偏差，最大幅值約為理想模型的1.76倍。整體而言，無論是幅值還是波動相比理想模型都相當大，說明間隙對滾針軸承的加速度與角加速度的影響非常大，對轉子系統的運行精度和可靠性影響較為顯著[11]。

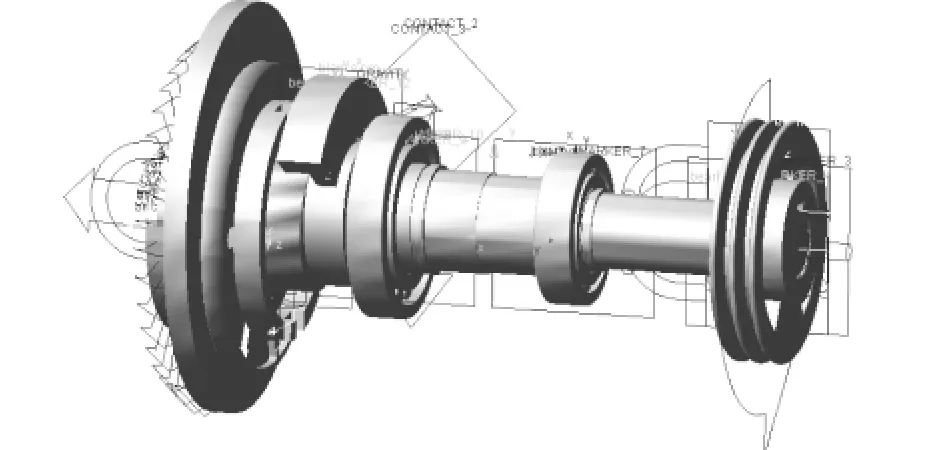
圖4 轉子系統連接關系

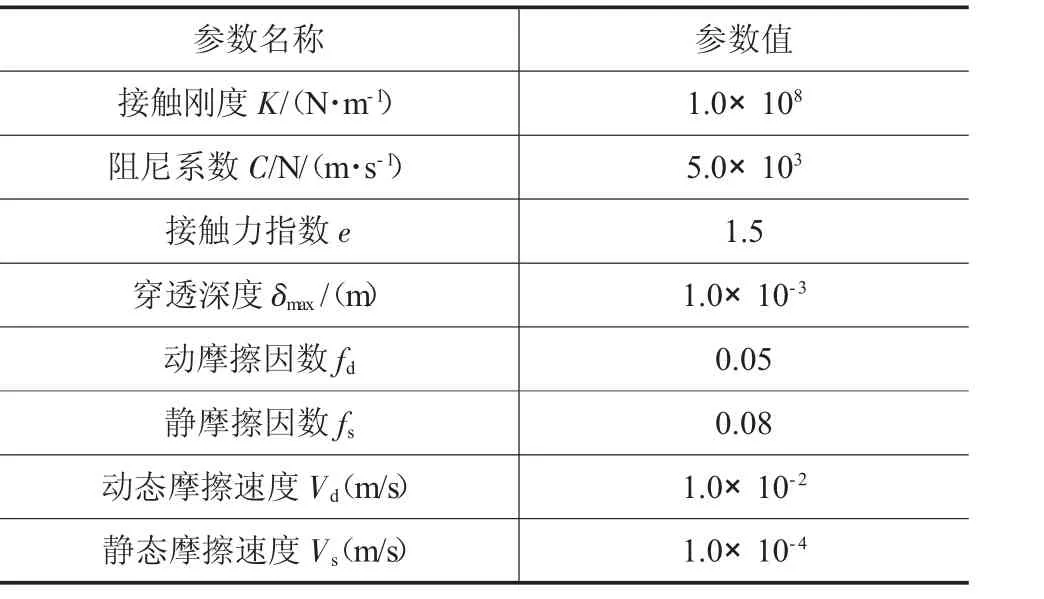
表3 仿真參數

由圖6可知，含間隙模型中的接觸碰撞力頻次和數值力明顯大于理想模型，對比圖5（c）可發現間隙鉸處接觸碰撞力的變化規律與加速度的變化類似，間隙大小變化的對滾針軸承的動態特性影響很大。具體表現為：隨間隙值的增加，曲柄銷與滾針軸承接觸碰撞力力的波動幅度增大但波動頻率相對減小。間隙值0.05 mm的模型的碰撞力相對理想模型明顯變大，同一時刻下二者最大差值約1684N，是理想狀態接觸力的2.53倍。一個曲軸旋轉周期內，傾覆力大小在689.57～811.48N區間內變化，接觸碰撞力在排氣角的位置出現峰值，受力呈現波浪形趨勢，即需要關注波峰值時軸承運動位置以及其受力情況，可以對軸承動力學做出預測。

由圖5和圖6可知，運動副的間隙對滾針軸承的位移和速度的變化影響相對較小，對滾針軸承加速度和接觸碰撞力的影響較大，且間隙值越大影響越明顯。這是由于運動副間隙值較小時，曲柄銷在滾針軸承發生碰撞前自由運動的時間相對較短，發生碰撞的時間也相對較短，而軸承位移和速度的改變需要時間，因此間隙模型的位移和速度相比理想模型變化不明顯，但間隙鉸處的接觸碰撞在極短時間內完成，因此軸承加速度和間隙鉸處碰撞力的曲線圖走勢類似，二者均呈現出脈沖式波動且數值大小不斷變化。但是運動副間隙增大時，軸承與曲柄銷發生碰撞前的運動時間會相對增加，則二者碰撞的次數會降低但碰撞前的速度會增大，導致運動副間隙處的加速度和接觸碰撞力增大[12]。

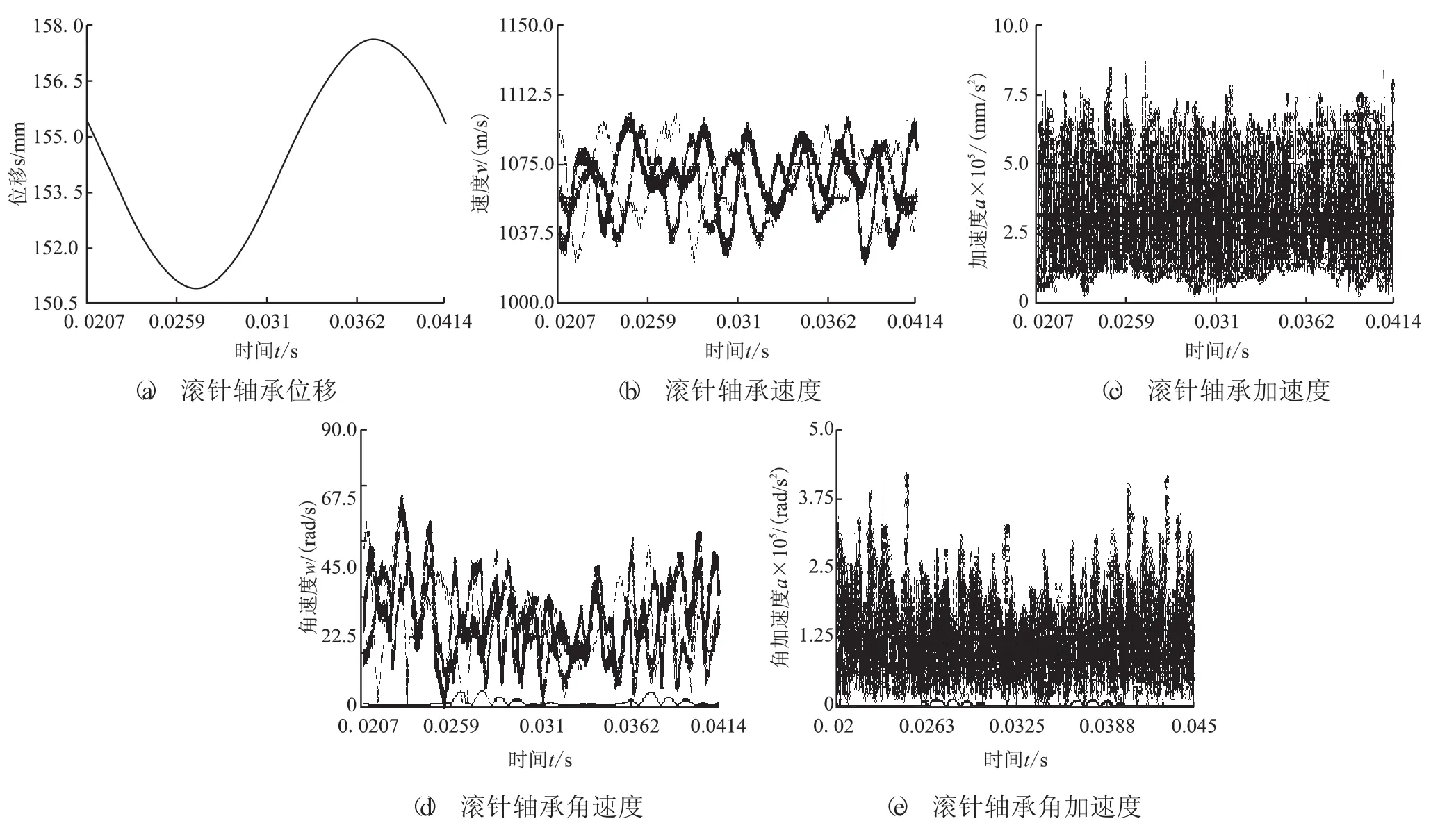
圖5 滾針軸承運動參數曲線圖

圖中7（a） 加粗實線表理想模型軸承質心運動軌跡，在不同間隙模型下間隙越大軌跡偏離距離越大；圖7（b） 可以很清楚看到間隙模型的質心軌跡在理想軌跡圓內發生碰撞，在軌跡圓外未發生碰撞。圖7（b） 中橫坐標-50.0041 mm至-50.6475 mm范圍內，間隙模型下軸承運動軌跡明顯進入理想運動軌跡，即該處發生較為嚴重的碰撞。計算發現，以該模型動渦盤渦齒正面建立平面二維坐標系，該碰撞區域為-136.5°至-155.46°范圍內。該臥式渦旋壓縮機的排氣角為坐標系-126°的位置，此處壓縮機開始排氣，壓縮腔中氣體力最大。即滾針軸承發生偏磨區域在排氣后19.11°范圍內，間隙與運動慣性使得磨損區域滯后于最大氣體力位置，此時碰撞力也處于峰值狀態加速了磨損，與實際情況相符具有指導意義。

6 結論

（1） 間隙的存在對滾針軸承位移幾乎沒有產生影響；對滾針軸承速度的影響較小；對滾針軸承加速度的影響較大，曲線出現脈沖式的波動；間隙的存在使軸承與曲柄銷的碰撞次數較頻繁，并且碰撞力幅值隨著間隙值的增大而增大。

（2） 滾針軸承存在固定偏磨區，為排氣角后19.11°范圍內。間隙值越大，滾針軸承質心運動軌跡的偏差越大，滾針軸承的磨損加劇，轉子系統的可靠性和運行穩定性變差。

（3）動渦盤傾覆的計入更真實地反映了渦旋壓縮機轉子系的動力特性，仿真結果表明壓縮機設計時應嚴格選用滾針軸承處的配合公差，以減少動渦盤傾覆造成的偏磨影響，提高軸承使用壽命。