例談離心率求解策略

劉清揚 河北省衡水市鄭口中學 河北省 衡水市 253000

離心率是描述圓錐曲線形狀特征的一個重要概念，是橢圓、雙曲線、拋物線三類二次曲線的統(tǒng)一定義的橋梁和紐帶.離心率問題內(nèi)涵豐富且綜合性強，是各級訓練測試及高考中的熱點之一.下面結(jié)合實例，分析求解圓錐曲線離心率的常用的“策略”.

策略一 借助公式、定義

根據(jù)圓錐曲線的標準方程或a、b、c對應的值，直接利用離心率公式來求解離心率的問題，關(guān)鍵在于求圓錐曲線的標準方程或a、b、c對應的值.

策略二 借助方程

根據(jù)題設條件，借助a、b、c之間的關(guān)系，求出關(guān)于a、c的方程關(guān)系式，進而得到關(guān)于離心率e的方程，從而通過解方程來得到離心率e，關(guān)鍵是構(gòu)造相應的方程，但解方程時要注意對應圓錐曲線的離心率的特征.

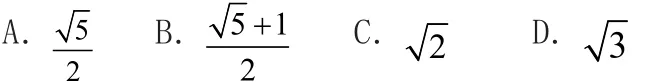
策略三 借助統(tǒng)一定義

由圓錐曲線的統(tǒng)一定義知，圓錐曲線的離心率e是平面上動點到焦點的距離和動點到準線的距離之比，特別適用于條件含有焦半徑的圓錐曲線問題及其他相關(guān)問題。關(guān)鍵是抓住圓錐曲線的統(tǒng)一定義，結(jié)合題意求解.

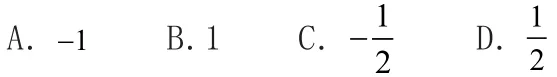
策略四：借助平面幾何知識，或圓錐曲線上點坐標的范圍

根據(jù)題設中的條件建立a、b、c之間的不等式關(guān)系，進而得到關(guān)于離心率e的不等式，通過求解不等式來求離心率的范圍，關(guān)鍵是構(gòu)造相應的不等式，但解不等式時要注意對應圓錐曲線的離心率的特征.