活塞風作用下雙豎井隧道內微波折射率結構常數的估算模型*

孫華清 趙恒凱

(上海大學通信與信息工程學院，200444，上海//第一作者，碩士研究生)

無線電波傳播會受到大氣湍流的影響，進而影響無線通信的質量。大氣折射率結構常數是一個反映湍流強度的物理量,可以用來描述無線電波受湍流影響程度。

為了深入了解大氣湍流對光波及電波傳輸的影響，文獻[1-5]等探討了多種環境下的湍流強度，建立了相應的折射率結構常數估算模型，為湍流領域的研究奠定了一定的理論基礎。

本文在Monin-Obukhov相似性原理的基礎上，對雙豎井隧道內由于列車運行產生的復雜空氣湍流場進行了分析探究和建模，推導出一種適用于雙豎井隧道內的折射率結構常數估算模型，為研究隧道內大氣湍流對無線電波傳播特性的影響提供理論參考。

1 湍流折射率結構常數估算模型

1.1 湍流折射率結構常數及與其結構參量的關系

在大氣環境下，大氣折射率n可以表示為

n=1+N×10-6

(1)

(2)

式中：

N——大氣折射率指數；

T——大氣溫度，K；

P——大氣壓強，hPa；

e——水汽壓，hPa；

Dn——折射率梯度，在微波頻段取77.6 K/hPa；

Hn——高度常數，在微波頻段取4 810 K/hPa。

當T=288.15 K時，飽和水汽壓es=17.12 hPa，相對濕度HR取值0～100。依據氣象統計資料[6]，水汽壓e的計算式為：

(3)

其中，e單位為hPa。

比濕q也可以表示為[7]：

(4)

結合式(2)—(4)可得，微波段大氣折射率的簡化計算式為：

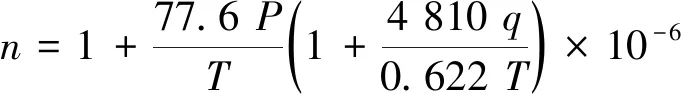
(5)

根據Kolmogorov的局部均勻各向同性原理，在湍流慣性子區間內，空間兩點間的折射率結構函數可以定義為：

(6)

式中：

r——空間兩點間距離；

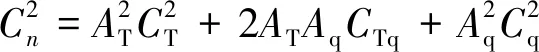
(7)

式中：

AT——大氣折射率對溫度的偏導；

Aq——大氣折射率對濕度的偏導；

CT——大氣折射率溫度結構函數；

Cq——大氣折射率濕度結構函數；

CTq——溫濕度相關結構函數。

在微波段，有

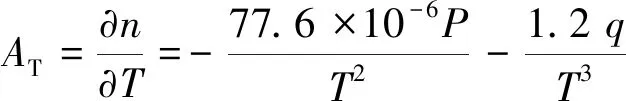
(8)

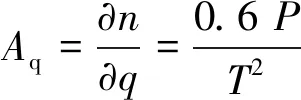
(9)

(10)

式中：

fT(z/L)、fq(z/L)及fTq(z/L)——分別為與溫度、濕度及溫濕度相關的穩定度參數經驗公式。

rTq——溫濕度相關系數，取值與波文比Bo的正負有關；當Bo≥0時，rTq≈0.8；當Bo<0時，rTq≈0.5。

z——高度。

L——M-O(Monin-Obukhov)長度，z/L為穩定度參數。有：

(11)

式中:

k——卡爾曼常數，通常取0.4;

g——重力加速度；

u0——摩擦速度。

根據文獻[10]，在不穩定層結條件下,有：

z/L<0

(12)

1.2 雙豎井隧道內的活塞風對的影響

活塞風速大小會直接影響區間隧道內的溫度及濕度狀況。列車在區間隧道內運行時，由于隧道壁面的限制，列車對隧道空氣產生推動作用，列車車頭處呈現正壓，車尾部分則為負壓，在這樣的壓差作用下，一部分氣體被推出隧道出口和豎井出口，一部分則從車頭經過列車和隧道間的環狀空間流到車尾。

當列車在長度為L2區段行駛時，由連續性方程得

Av=A5v5+Av3

(13)

或

Av=A4v4+Av2

(14)

式中：

A——隧道平均橫截面積；

A4——左側豎井橫截面積；

A5——右側豎井橫截面積；

v——長度為L2區段氣流速度；

v2——長度為L1區段氣流速度；

v3——長度為L3區段氣流速度；

v4——左側豎井內氣流速度；

v5——右側豎井內氣流速度。

如圖1所示，可先建立列車前緣斷面1-1與列車尾部斷面6-6之間的能量方程：

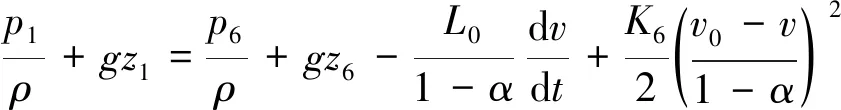
(15)

式中：

λ——沿程阻力系數；

K6——氣流在環狀空間中的阻力系數；

pi——在隧道i處的局部阻力壓降；

zi——隧道i處的高度；

ρ——空氣密度；

v0——隧道空間下墊面風速；

α——隧道阻塞比。

圖1 列車在隧道雙豎井之間行駛示意圖

建立列車前緣斷面1-1與隧道出口斷面3-3之間的能量方程：

式中：

ξ出——隧道出口局部阻力系數。

建立左豎井進口斷面4-4與隧道斷面7-7之間的能量方程：

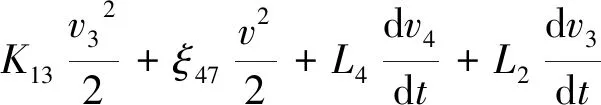
(17)

式中：

K13——氣流由左豎井匯入隧道長度為L2區段的阻力系數；

ξ47——左豎井中的氣流匯入隧道長度為L3區段的局部阻力系數。

右豎井進口斷面5-5與隧道斷面8-8之間的能量方程為：

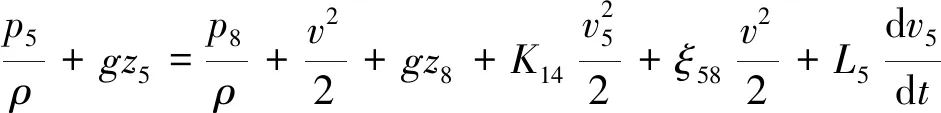
(18)

式中：

K14——氣流進入左豎井隧道的阻力系數；

ξ58——右豎井中的氣流匯入隧道段長度為L3區段的局部阻力系數。

綜合式(15)—(19)，可以求得長度為L2區段中的活塞風速v活為：

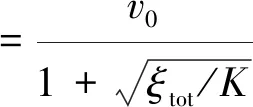
(19)

式中：

ξtot——雙豎井隧道的總阻力系數。

K——雙豎井隧道的總活塞作用系數。有：

(20)

1.3 雙豎井隧道內M-O長度的確定及建模

根據Monin-Obukhov相似性理論，雙豎井隧道內風速v、溫度T以及比濕q的無量綱輪廓線可分別表示為

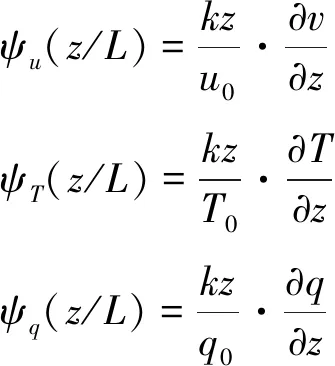
(21)

u0、T0、q0可以分別表示為：

(22)

式中：

Δv、ΔT、Δq——隧道空間一點z1與參考點z0之間的風速差、溫度差和濕度差。

根據文獻[11-12]的經驗公式可知：

在不穩定大氣環境下，即z/L<0時

(23)

(24)

將式(23)—(24)代入式(11)，可以得到不穩定大氣環境下雙豎井隧道內的M-O長度為

(25)

綜上所述，結合式(7)，可將雙豎井隧道的大氣折射率結構常數表示為：

(26)

綜合式(8)、(9)、(24)及(25)，可得活塞風作用下的雙豎井隧道內的大氣折射率結構常數表達式：

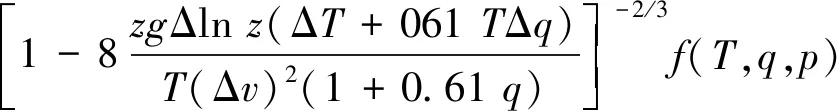
(27)

其中,Δv=v活-v0，v活為活塞風速，f(T,q,p)是雙豎井隧道環境下與溫度、濕度及壓強相關的函數：

1.2rTqPTΔTΔq(77.6×10-6PT+1.2q)+(0.6PTΔq)2]

(28)

2 仿真試驗

2.1 仿真試驗基本數據

基于上海軌道交通2號線部分區間隧道的數據，使用MATLAB仿真軟件，對隧道環境內的微波段的折射率結構常數進行仿真分析。

上海軌道交通2號線全長約27 km，其車輛、供電、接觸網及通信等系統由德國戴姆勒-奔馳交通公司和西門子公司提供。列車為8節編組，每節車廂的長、寬、高分別為23.54 m、3.00 m、3.80 m，列車運行速度約為75 km/h。取南京西路站—靜安寺站區間隧道作為研究對象。隧道內高度為2.00 m，長度約為1.37 km，平均截面面積為30.15 m2。隧道內參考面溫度T0=288 K，參考面上的水平風速為2 m/s，大氣壓強P取1 013 hPa。由于隧道內底部濕度較大，參考面的相對濕度取HR=60。雙豎井隧道內沿程阻力系數λ取0.05，雙豎井隧道局部阻力系數ξtot取0.5，溫度差(T-T0)為活塞風作用下的隧道內空氣與參考面的氣溫差。

2.2 不同活塞風速條件下的仿真

圖2是在雙豎井隧道內不同活塞風速條件下，大氣折射率結構常數隨著溫度差的變化曲線。

由圖2可見，當溫度差的絕對值較小時，即|T-T0|<10，隨著|T-T0|的增大，隧道內大氣折射率結構常數大幅增大。可見，溫度差變化對雙豎井隧道內的大氣折射率結構常數影響顯著。當溫度差在一定范圍時，隨著活塞風速的增大，雙豎井隧道內大氣折射率結構常數增大。與活塞風速變化相比較，溫度變化對于大氣折射率結構常數變化的影響更加顯著。

圖2 不同活塞風速v下溫度差和大氣折射率結構常數之間的關系

2.3 不同豎井條件下的仿真

為了探究雙豎井隧道環境對于湍流強度的影響，運用上述參數，并取活塞風速為12 m/s,隧道長度均為1 370 m，對不同豎井條件情況下的折射率結構常數進行仿真比較。仿真結果如圖3所示。

圖3 不同豎井條件下隧道溫度與大氣折射率結構常數之間的關系

由圖3可知，與無豎井、單豎井隧道環境比較，雙豎井隧道內湍流強度較后兩者都小，且溫度升高時，雙豎井的通風效果更加明顯，因此，雙豎井有效降低了隧道內湍流強度，有利于無線通信系統性能的提高。

2.4 不同雙豎井間距條件下的仿真

取活塞風速為12 m/s，分別對雙豎井間距Ld為0.5 km、1.0 km及1.5 km的隧道進行不同溫度差的仿真分析。仿真分析結果見圖4。

由圖4可以看出，隨著雙豎井間距的不斷增加，隧道內湍流強度也不斷增大。這是因為雙豎井間距變大后，隧道內通風效果變差，使列車周圍氣流運動空間相對變小，單位體積空間內空氣溫濕度的變化加快。此外，豎井間距的調整可以大幅改變大氣折射率結構常數。只有當雙豎井間距趨于極限值時，大氣折射率結構常數變化才不再明顯。這是因為間距足夠大時，雙豎井通道類似于無豎井隧道，不再有明顯的通風效果。

圖4 不同雙豎井間距下溫度差和大氣折射率結構常數之間的關系

為了進一步探究活塞風速與湍流強度的關系，還對雙豎井間距Ld為0.5 km、1.0 km及1.5 km的隧道，針對不同活塞風速進行仿真分析。仿真分析結果見圖5。

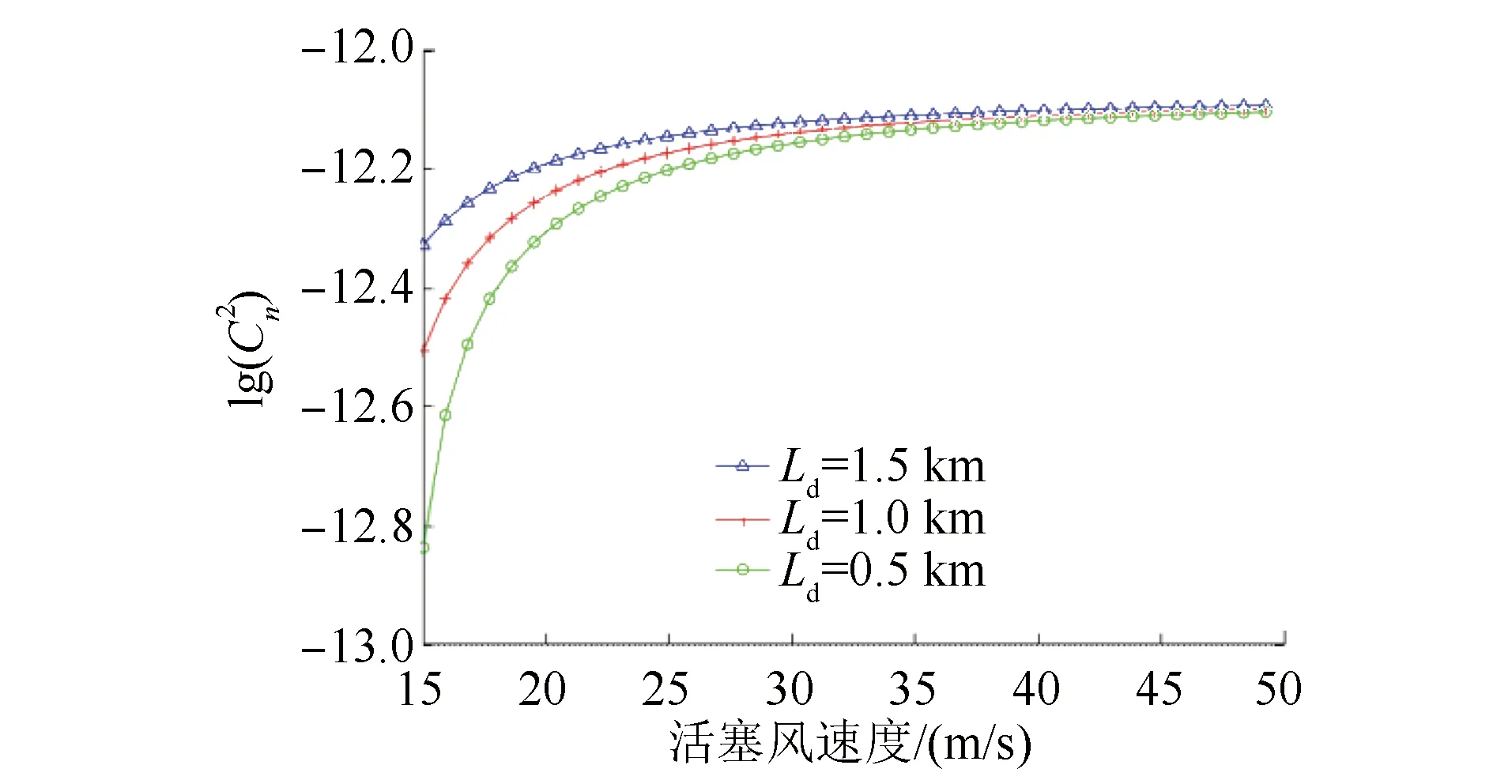
圖5 不同雙豎井間距下活塞風速度與大氣折射率結構常數之間的關系

由圖5可見，雙豎井隧道環境中，隨著列車速度的增大，活塞風速度增大，加劇了隧道內湍流變化，致使大氣折射率結構常數呈上升趨勢。

由圖5還可看出：豎井間距對于活塞風的作用效果也造成影響，豎井間距增大則活塞風所導致的大氣折射率結構常數變化的動態范圍趨小；當活塞風速足夠大時，隧道內的大氣折射率結構常數已經趨于極限值，故雙豎井間距對于隧道內湍流強度的影響也不再明顯。

3 結語

本文利用近地層相似形理論以及Bulk方法，采用Frederickson公式，結合雙豎井隧道活塞風的運動特性，計算出溫度結構常數、濕度結構常數和溫濕度結構函數，建立了雙豎井隧道不穩定空氣環境下的大氣折射率結構常數估算模型。

通過對實例項目的仿真分析可知：

1) 雙豎井隧道環境下空氣湍流大氣折射率結構常數的數量級為10-15～10-11；雙豎井有效降低了隧道內湍流強度，與單豎井隧道相比較，湍流強度至少降低了2個數量級。

2) 阻塞比對于雙豎井隧道的影響比單豎井隧道更弱；豎井間距對于活塞風的作用效果也造成影響，豎井間距增大則活塞風所導致的大氣折射率結構常數變化的動態范圍趨小；而當活塞風速足夠大時，雙豎井間距對于隧道內湍流強度的影響也不再明顯。

3) 雙豎井隧道環境下，列車速度在超過一定范圍后，或者列車速度較大時，其對湍流強度的影響將不再明顯。

綜上所述，通風雙豎井能有效降低大氣折射率結構常數，進而降低湍流對電波傳播的影響，有利于隧道內無線電波的傳輸。