基于屬性分區的（αi，k）-p隱私保護算法

摘 要：針對（αi，k）—匿名算法使用有損鏈接思想無法對用戶身份進行保護的問題，引入屬性分區置換概念，提出基于屬性分區的（αi，k）-p匿名算法，對桶中QI屬性采取分區、置換的方式保護用戶身份信息。在人口真實數據集21 956條數據上對兩種算法進行敏感值保護和會員身份保護有效性對比實驗。結果表明，敏感值泄露概率最高時只剛好超過0.05，接近傳統方法的1/4;在會員身份保護方面，FOR值在0.7以上。相對于（αi，k）—匿名算法，該算法能更好地保護敏感值信息和會員身份信息。

關鍵詞：隱私保護;數據發布;屬性分區

DOI：10. 11907/rjdk. 191457 開放科學（資源服務）標識碼（OSID）：

中圖分類號：TP312 文獻標識碼：A 文章編號：1672-7800（2019）008-0063-03

（αi，k）-p Privacy Preserving Algorithm Based on Attribute Partition

WU Shao-xin

（College of Computer Science and Engineering， Shandong University of Science and Technology， Qingdao 266590， China）

Abstract： The （αi，k）-anonymity algorithm proposed by Jinhua uses the idea of lossy links， and it can not provide the protection of user identity. In this paper， the idea of attribute partition replacement is introduced， and an （αi，k） - p anonymity algorithm based on attribute partition is proposed. QI attribute partition and replacement in bucket are adopted to protect user's identity information. This paper implements two algorithms for 21 956 data sets of real population， and compares the effectiveness of sensitive value protection and membership protection. The results show that the leakage probability of sensitive value is just over 0.05， which is close to 1/4 of the traditional method， and FOR value is above 0.7 in membership protection. Compared with （αi，k）-anonymous algorithm， the proposed algorithm can better protect sensitive value information and membership information.

Key Words： privacy protection; data publishing; attribute partition

作者簡介：武紹欣（1995-），男，山東科技大學計算機科學與工程學院碩士研究生，研究方向為網絡安全、隱私保護。

0 引言

隨著計算機技術的快速發展，數據交互越來越方便，大量數據被政府機構或企業收集[1-2]，對此進行數據挖掘等研究，能幫助決策并創造商業價值，但也存在個人隱私泄露風險[3-5]。因此，隱私保護越來越受到重視。但對數據過分保護使挖掘的信息減少，因此隱私保護研究的重點是在數據可用性與隱私保護之間求得平衡。

現有的隱私保護技術大體分為數據失真、數據加密和限制發布3類[6]。數據失真技術主要通過添加噪聲等方式使數據失真，從而達到保護數據隱私的目的;數據加密是通過加密算法實現數據的隱私保護;限制發布則是將數據中的隱私信息先進行泛化或匿名等操作后再發布，限制性地發布處理后的數據。

Sweeney等[7]通過對數據匿名化研究提出k—匿名模型，該模型對數據表中的準標識符屬性進行約束，要求發布的數據表任意一條記錄，在準標識符屬性上都無法與其它 k-1 條記錄區分，這樣即使攻擊者能夠了解目標用戶的所有QI信息，也無法確切知道用戶的敏感信息。

為克服 k—匿名模型難以抵御同質性攻擊的缺陷，Machanavajjhala A等[8]提出了l—多樣性匿名方法，要求在同一等價類中都有l個表現良好的敏感值，解決了某些情況下由于敏感屬性取值單一導致的隱私泄漏問題。但是該模型下的數據集會有遭受到偏斜攻擊和相似性攻擊的可能。

Li等[9]提出t—接近模型，它要求每個等價類中所有敏感值的分布要與原始數據表中敏感值的分布接近，差異不要超過預先設定的閾值，但是沒有給出具體算法，且由于較為嚴格的限制致使該模型難以實現。

隨后，Wong等[10]提出了（α，k）—匿名模型。（α，k）—匿名模型要求匿名數據集在等價組上滿足k值約束條件下，任意敏感屬性值在等價組中出現的概率都小于等于α值約束，即0≤α≤1。

解剖[11]與泛化和抑制不同，該方法在兩個單獨的表中給出關于QI和SA上的數據：包含QI屬性的QIT、包含SA的ST以及QIT和ST都具有一個共同屬性，即組ID。解剖學的最大好處是QIT和ST都沒有數據修改。

這些方案可以應對一些攻擊類型，如背景知識攻擊[12]和合成攻擊[13]等，但依然有別的攻擊方式不能抵御，如相似性攻擊和敏感性攻擊。

在上面模型基礎上，姜火文[14]提出基于貪心的聚類算法，減小了信息損失，但不能應對敏感性攻擊。張健沛[15]提出基于敏感值語義桶分組的隱私保護模型;曹敏姿[16]提出個性化（α，l）-多樣性k-匿名模型，可以應對敏感性攻擊，但卻改變了一些元組的敏感值;毛慶陽[17]提出基于聚類的S-KACA算法，能夠提供敏感性保護，但存在很多等價類沒有最小化，增加了信息損失;劉湘雯[18]提出了個性化擴展（α，k）匿名模型，根據敏感度將敏感屬性值分為若干組，每組都有自己的頻率約束閾值，為每個人設置一個保護節點，必要時替換敏感值，但該模型同樣改變了一些元組的敏感值。

金華[19]提出（αi，k）—匿名模型，預先設置每個敏感值的敏感級別，然后在一個桶中限制所有級別敏感值的頻率從而實現對隱私的保護。一個等價類中，任意一條元組的敏感值比例不高于α，且任意級別的敏感值占比均不超過閾值αi，則稱該等價類滿足（αi，k）—匿名，但它無法提供會員身份保護。

為改善（αi，k）-匿名模型缺點，本文提出一種基于屬性分區的（αi，k）-p匿名算法，在選取元組構成等價類之前先對元組中的QI信息進行分區，在構成等價類后再置換QI組。該算法在會員身份保護和敏感值保護方面均有很大優勢，可應對敏感性攻擊。

1 基于屬性分區的（αi，k）-p算法

（αi，k）-anonymity模型無法對身份信息進行保護，因此算法需對屬性進行分區，使高度相關的屬性位于同一列中，這有利于實用性和隱私性。在數據實用性方面，將高度相關的屬性分組以保留這些屬性之間的相關性。在隱私方面，不相關屬性的關聯比高度相關屬性的關聯具有更高的識別風險，因為不相關屬性值的關聯頻率要低得多，更容易識別。為保護隱私，就要打破不相關屬性之間的關聯，具體算法如下：

算法

輸入：原始數據表T，參數k，敏感性分級（L1，L2，…，Li，…），頻率約束（α1，α2，…，αi，…）

輸出：置換匿名表Tanony

步驟如下：

使用均方偶然系數計算出QI屬性中的相關度;

使用PAM聚類算法對列屬性進行聚類;

將T中每個元組的的QI值按照列聚類的結果使用集合代替;

[j=max（1α，k），θi=j？αi，i=1，2，？];

while 剩余元組可以構造元組桶;

E=Φ;

while 元組桶E不滿足（αi，k）匿名;

在所有級別的 Li中按照級別從高到低的順序一次選取敏感屬性為個數最多的元組加入元組桶E，在T中取出該元組，且在下一次選擇當前敏感級時跳過該敏感值的元組;

檢查在每一級別挑選的個體個數是否小于對應的θi，如果不小于θi，則下一次選取個體時跳過該敏感級。如果當前敏感級除去選擇的SA為空，則下次選擇SA時跳過該敏感級;

end while;

將E中每一列隨機置換;

將E添加到Tanony，并標注classID;

end while;

對于剩余的元組，添加到某個元組桶中，該元組桶仍然滿足（αi，k）匿名，則將該元組添加到該等價類中。

隱匿所有的無法添加到等價類的元組;

輸出匿名表Tanony。

給定兩個屬性A1、A2，其中值域分別為{V11，V12，…，V1d1}、{V21，V22，…，V2d2}，其對應的值域大小分別是d1、d2。A1、A2之間的均方偶然系數計算方法如公式（1）所示。

[φ2（A1，A2）=1min（d1，d2）-1i=1d1j=1d2（fij-fi？f？j）2fi？f？j]? ? （1）

其中[fi？]、[f？j]分別是數據表中V1i、V2j，[fij]表示數據表中的數目。

2 實現方法

硬件環境：Intel（R） Core（TM）i5-3230M CPU@2.6GHz，內存4G，操作系統Win7 x64旗艦版;軟件環境：使用python編程語言實現，IDE開發工具為Pycharm。

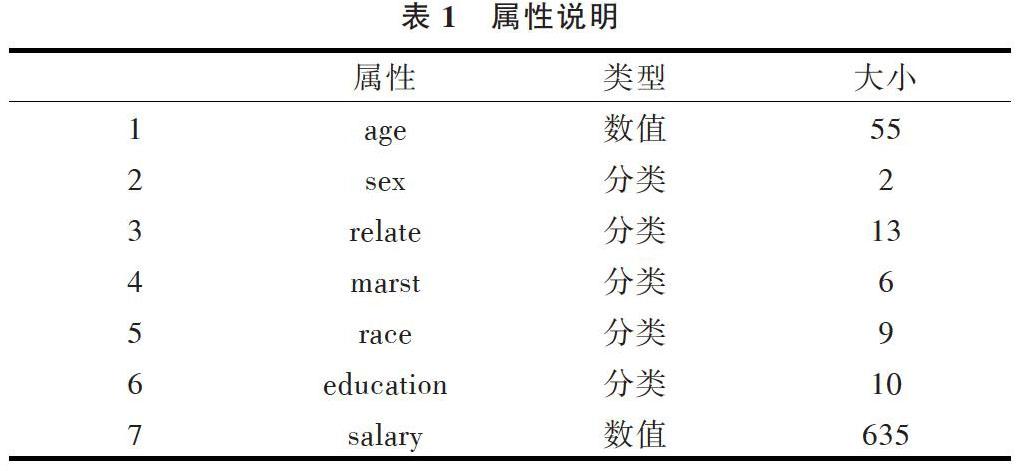
本文使用真實的美國人口普查數據作為實驗數據[20]，去除其中的無效數據，隨機挑選21 956條數據。其中，age、sex、relate、marst、race、education作為QI屬性，salary作為敏感屬性，詳細信息如表1所示。

表1 屬性說明

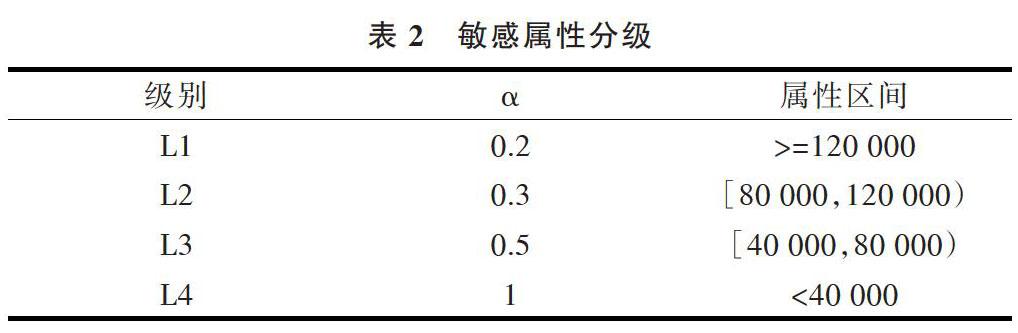
對數據集中敏感屬性salary的屬性值采用如表2所示的分級，并設置在同一合并桶中每一級別敏感屬性出現的頻率。

表2 敏感屬性分級

2.1 敏感值泄露概率

假定攻擊者已經了解所有用戶的QI信息，并且知道用戶在這種匿名表上，攻擊者通過將QI值匹配該匿名表獲得敏感信息。下面通過敏感值泄露概率[21]驗證算法對敏感值的保護能力。

選擇任意一個元組t，計算t的匹配個體數量Numtuples（t），匹配桶MB中t的匹配個體數量，記作Num（t，MB），以及t的敏感值s在MB中出現的次數Num（t，MB），[MB]表示MB中包含個體的數量，計算公式如下：

[p（t，s）=MBNum（t，MB）？Num（s，MB）Numtuples（t）？MB] （2）

2.2 偽元組比率

使用偽元組比率[22]驗證兩個算法對會員披露的保護，定義為偽元組的數量除以總元組的數量。FOR越大，提供的會員披露保護越多。計算公式如下：

[FOR=tuplefaketupleall]? ? ? ? ?（3）

假定每個桶有k個元組，被分為c列，每列有k個不同的值，那么偽元組個數為kc-k個，FOR=1-1/kc-1。

3 實驗結果

采用（αi，k）-pGCA算法和（αi，k）-GCA算法[19]對數據集進行匿名分析。取k為固定值5，c值為2，隨著α值的變化，對比兩種算法結果。首先對比兩個算法的敏感值泄露概率，結果如圖1所示。

圖1 敏感值泄露概率

因為（αi，k）-GCA算法完全沒有對元組的QI值提供保護，所以所有的元組幾乎能百分之百匹配到所在的元組桶，因此該算法對敏感值的保護取決于元組桶大小。而（αi，k）-pGCA算法對QI值分區，并對每一個元組桶內的QI值置換，所以對每一個元組都能匹配到多個元組桶，因此敏感值泄露概率遠低于（αi，k）-GCA算法。在敏感值保護方面，（αi，k）-pGCA算法更好。

每次實驗值選取1 000個元組桶，計算FOR的平均值，對比結果如圖2所示。

圖2 偽元組比率

因為（αi，k）-GCA算法對QI值做匿名操作，所以在一個元組桶中不會產生任何偽元組，因此FOR都為0。（αi，k）-pGCA算法的元組桶中產生更多的元組，偽元組比率隨著元組桶的增大而增大，在α取到1/15及更小時，元組桶中偽元組的比重已經占到絕大多數，能更好地應對會員身份披露。

4 結語

為解決現有（αi，k）-GCA算法無法保護身份和無法應對會員身份披露的問題，本文提出一種新的（αi，k）-pGCA算法。通過對原始數據集元組的QI信息進行分區置換，可以更好地保護隱私信息。可以看到，在分區置換后，敏感值泄露概率遠遠超過需求。未來將通過優化算法進一步研究如何最小化元組桶大小，使其既符合隱私保護需求，又能減少后續數據分析誤差。

參考文獻：

[1] 馮登國，張敏，李昊. 大數據安全與隱私保護[J]. 計算機學報， 2014， 37（1）：246-258.

[2] 閆蒲. 互聯網社交大數據下行為研究的機遇與挑戰[J]. 中國統計，2016（3）：15-17.

[3] 王博. 大數據發展背景下網絡安全與隱私保護研究[J]. 軟件導刊，2016， 15（8）：171-172.

[4] 劉雅輝，張鐵贏，靳小龍，等. 大數據時代的個人隱私保護[J]. 計算機研究與發展，2015，52（1）：229-247.

[5] 孟小峰，張嘯劍. 大數據隱私管理[J]. 計算機研究與發展， 2015， 52（2）：265-281.

[6] JIA J J，YAN G L，XING L C. Personalized sensitive attribute anonymity based on p-sensitive k anonymity[C]. International Conference on Intelligent Information Processing. ACM， 2016： 54.

[7] SWEENEY L. K-anonymity： a model for protecting privacy[J].? International Journal of Uncertainty， Fuzziness and Knowledge-Based Systems， 2002， 10（5）： 557-570.

[8] MACHANAVAJJHALA A，GEHRKE J，KIFER D， et al. L-diversity： privacy beyond k-anonymity[C]. Atlanta：Proceedings of the 22nd International Conference on Data Engineering，2006： 24-24.

[9] LI N，LI T，VENKATASUBRAMANIAN S. t-Closeness： privacy beyond k-anonymity and l-diversity[C]. 2007 IEEE 23rd International Conference on Data Engineering. IEEE Computer Society， 2007.

[10] WONG R C， LI J， FU A W， et al. （α，k）-Anonymity： an enhanced k-anonymity model for privacy preserving data publishing[C].? Proceedings of the 12th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining，2006：754-759.

[11] XIAO X ，TAO Y.Anatomy： simple and effective privacy preservation[C]. Proceedings of the 32nd International Conference on Very Large Data Bases， 2006，139-150.

[12] 谷汪峰，饒若楠. 一種基于K-anonymity模型的數據隱私保護算法[J]. 計算機應用與軟件，2008（8）：65-67.

[13] 焦佳. 社會網絡數據中一種基于K-degree-l-diversity匿名的個性化隱私保護方法[J]. 現代計算機：專業版，2016（29）：45-47，60.

[14] 姜火文，曾國蓀，馬海英. 面向表數據發布隱私保護的貪心聚類匿名方法[J].? 軟件學報， 2017，28（2）：341-351.

[15] 張健沛，謝靜，楊靜，等. 基于敏感屬性值語義桶分組的T-closeness隱私模型[J]. 計算機研究與發展，2014，51（1）：126-137.

[16] 曹敏姿. 微數據發布中的個性化隱私保護方法研究[D]. 烏魯木齊：新疆大學， 2018.

[17] 毛慶陽，胡燕. 基于聚類的S-KACA匿名隱私保護算法[J]. 武漢大學學報：工學版， 2018，51（3）：276-282.

[18] LIU X W，XIE Q Q，WANG L M. Personalized extended （α， k）-anonymity model for privacy preserving data publishing[J]. Concurrency & Computation Practice & Experience， 2016，33（2）：55-67.

[19] 金華，張志祥，劉善成，等. 基于敏感性分級的（αi，k）-匿名隱私保護[J]. 計算機工程，2011，37（14）：12-17.

[20] DOCIN[EB/OL]. https：//usa.ipums.org/usa/index.shtml

[21] LI T，LI N，JIAN Z，et al. Slicing： a new approach for privacy preserving data publishing[J]. IEEE Transactions on Knowledge & Data Engineering，2012， 24（3）：561-574.

[22] LI B，LIU Y，XU H，et al. Cross-bucket generalization for information and privacy preservation[J]. IEEE Transactions on Knowledge & Data Engineering，2017，30（3）：449-459.

（責任編輯：杜能鋼）