稀疏度自適應回溯追蹤算法改進

丁佳靜 武雪姣 李雪晴

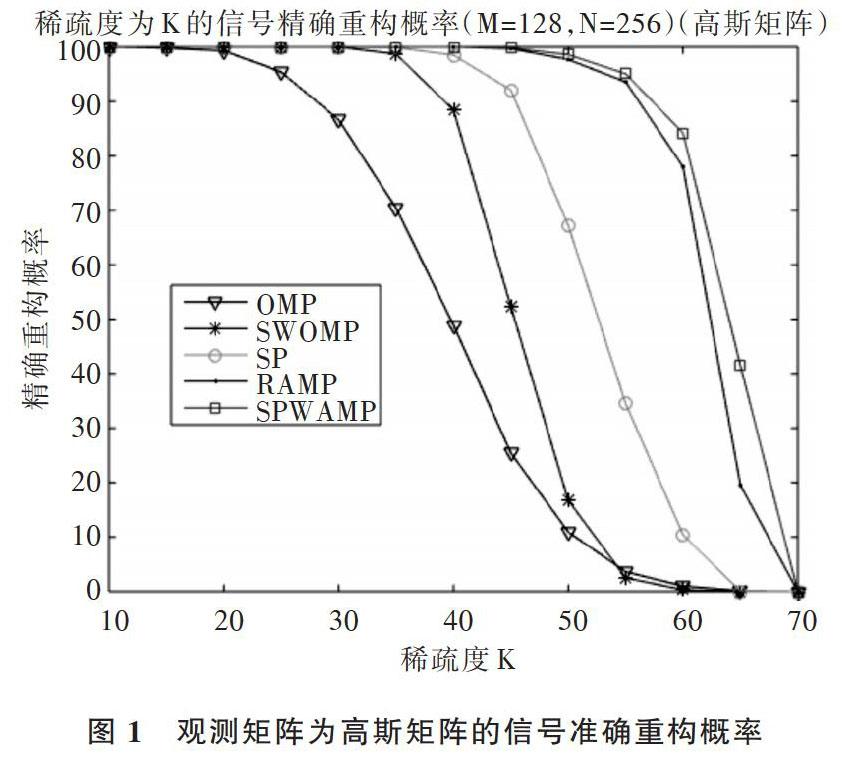
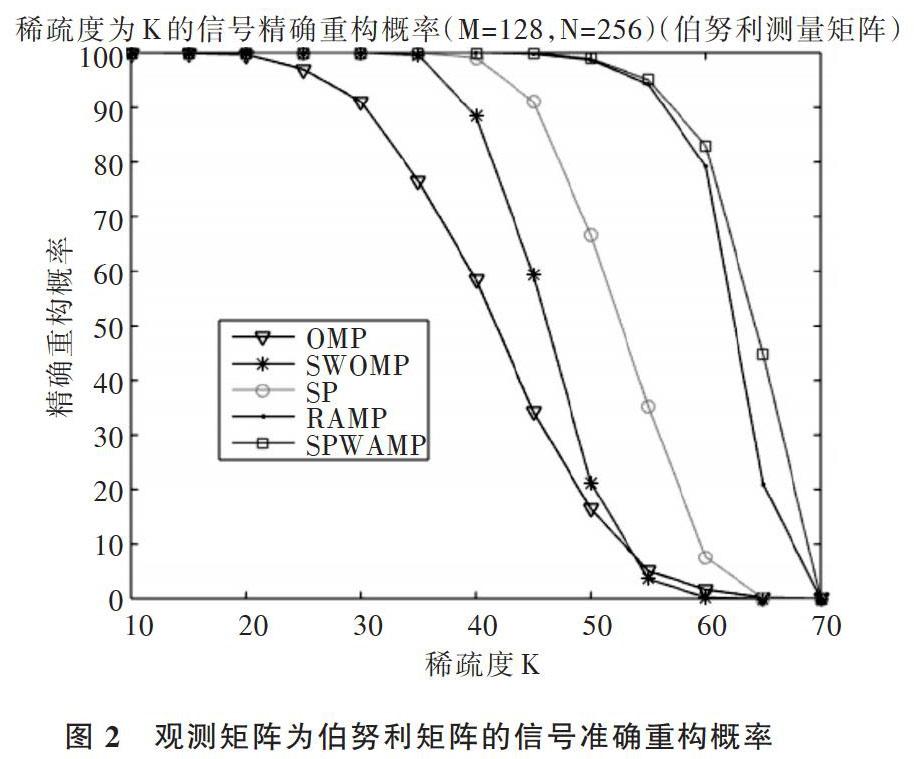
摘 要：針對壓縮感知重構算法中信號稀疏度未知和步長大小固定的問題，提出一種新的壓縮感知信號重構算法，即基于弱選擇的稀疏度自適應回溯追蹤（SPWAMP）算法。該算法將自適應思想、變步長迭代思想與回溯思想相結合，在未知信號稀疏度的情況下，利用閾值方法選取預選集，通過變步長更新支撐集原子個數并結合回溯思想剔除不可靠原子，最終實現信號精確重構。仿真結果表明，當信號稀疏度K達到65時，該算法重構精度相對稀疏度自適應匹配追蹤（SAMP）算法提高了40%，而此時正交匹配追蹤（OMP）算法、子空間追蹤（SP）算法和分段弱選擇正交匹配追蹤（SWOMP）算法已無法實現重構。因此，該算法相對其它同類算法提高了信號重構精度。

關鍵詞：壓縮感知;重構算法;稀疏度自適應;信號處理

DOI：10. 11907/rjdk. 191437 開放科學（資源服務）標識碼（OSID）：

中圖分類號：TP312 文獻標識碼：A 文章編號：1672-7800（2019）008-0059-04

Improved Algorithm for Sparsity Adaptive Backtracking

DING Jia-jing， WU Xue-jiao， LI Xue-qing

（School of Information Engineering， Hebei GEO University， Shijiazhuang 050000， China）

Abstract：Aiming at the reconstruction of unknown sparsity signal and step size small fixed in compressed sensing， we put forward a new compression sensing signal reconstruction algorithm， namely sparsity adaptive backtracking algorithm based on weak selection（SPWAMP）. The algorithm combines the idea of adaptive， variable step iteration and backtracking. In the case of unknown signal sparsity，the preset is selected by threshold method， and the number of atoms in the support set is updated by variable step size and the idea of backtracking is used to eliminate the unreliable. Finally， the precise signal reconstruction is realized. Simulation results show that when the signal sparsity K reaches 65， the reconstruction accuracy of the algorithm is improved by 40% compared with SAMP， while OMP， SP and SWOMP cannot realize the reconstruction. Therefore， compared with other similar algorithms， this algorithm improves the signal reconstruction accuracy.

Key Words：compressed sensing; reconstruction algorithm; sparse degree adaptive; signal processing

作者簡介：丁佳靜（1992-），女，河北地質大學信息工程學院碩士研究生，研究方向為人工智能與機器學習。

0 引言

2004年，Donoho[1]提出壓縮感知（Conmpressed Sensing，CS）理論，指出如果信號在某個變換域是稀疏的，則可借用一個觀測矩陣將變換后的信號降維;若該觀測矩陣滿足約束等距性條件，可以求解最優化問題，并根據低維測量向量，高概率地精確恢復原始信號。該理論在信號處理領域有廣闊的應用前景[2-5]。

壓縮感知理論主要由信號稀疏表示、測量矩陣構造和重構信號算法組成，其中，最核心的是重構算法[6-9]，其代表性算法包括正交匹配追蹤（Orthogonal Matching Pursuit，OMP）算法[10]、子空間追蹤（Sub-space，SP）算法[11]、正則化正交匹配追蹤（Regularized Orthogonal Matching Pursuit，ROMP）算法[12]、分段正交匹配追蹤（Stagewise Orthogonal Matching Pursuit，StOMP）算法[13]和稀疏度自適應匹配追蹤（Sparsity Adaptive Matching Pursuit，SAMP）算法[14]。2010年楊成等[15]提出一種新的稀疏度自適應子空間追蹤算法，該算法在每次迭代中采用弱匹配原則選取新原子，并引入SAMP自適應思想，再通過回溯思想提高重構準確性;2013年Xue等[16]提出VSStAMP（Variable Step size Stagewise Adaptive Matching Pursuit）算法，該算法根據判斷候選集中包含原子的個數作為變步長的標準，當原子個數小于u*M時采用大步長2*s，當原子個數小于u*M時采用小步長s。

本文在現有壓縮感知重構算法的基礎上，針對實際信號稀疏度大多未知及步長大小固定的問題，結合SP算法的回溯思想和SAMP算法的自適應思想，并運用弱匹配原則選取新原子和變步長思想，提出一種改進的基于弱選擇的稀疏度自適應回溯追蹤（Sparsity subspace Weak Adaptive Matching Pursuit，SPWAMP）算法。

1 壓縮感知理論

壓縮感知理論中待采樣的信號能夠實現壓縮感知技術的前提是該信號是稀疏的，即利用信號可壓縮性減少采樣樣本數目，且可以重建原始信號。壓縮感知與普通采樣率不同之處在于，測量對象不再是信號的某一采樣點數據，而是一組用于描述信號的線性方程[17-18]。

假設待采樣信號[x]的長度為[N]，觀測信號[y]的長度為[M]（[M<

[y=Φx]? ? ? ? ? ? ? ? （1）

[x]一般不是稀疏的，但在某個變換域[Ψ]是稀疏的，即[x=Ψθ]。此時[y=ΦΨθ]，令[A=ΦΨ]，則[y=Aθ]。其中[θ]表示[K]是稀疏的，即[θ]只有[K]個非零項，是信號[x]在某變換域的系數表示，[Φ]是大小為[M×N]的測量矩陣，[Ψ]是大小為[N×N]的稀疏矩陣，[A]是大小為[M×N]的傳感矩陣。

根據觀測值[y]，利用稀疏重構關系和重構算法重構信號[x]，可求解[l1]范數優化問題：

[minαα1s.t.y=Ax]? ? ? ? （2）

從觀測值[y]中恢復稀疏系數[θ]，進而求出信號[x]的精確估計[19-20]。

2 基于弱選擇的稀疏度自適應回溯追蹤算法

壓縮感知中子空間追蹤（SP）算法在每次迭代中選擇多個原子，利用回溯思想，在每次迭代過程中重新估計所有候選者的可信賴性，但其自身也有不足，必須以稀疏度作為輸入參數。

2.1 SP算法

SP 算法核心步驟：

輸入：[M×N] 傳感矩陣[A]

[N]維觀測向量[y]

信號稀疏度[K]

（1）初始化[r0=y，Λ0=φ，A0=φ，t=1]。

（2）計算內積[u=abs[ΑTrt-1]]（即計算[rt-1，aj]，[1][jN]），選擇[u]中[K]個最大值，將這些值對應[Α]的列序號[j]構成集合[J0]（列序號集合）。

（3）令[Λt=Λt-1？J0]，[Αt=Αt-1？aj][（j∈J0）]。

（4）從[θt]中選出絕對值最大的[K]項記為[θtK]，對應[At]中[K]列記為[AtK]，對應[A]的列序號記為[ΛtK]，更新集合[Λt]=[ΛtK]。

（5）求[y=Αtθt]的最小二乘解：[θt=argminθ||y-Αtθt||=][（ΑTtAt）-1ATty]。

（6）更新殘差，使得[rt=y-ΑtKθtK=y-ΑtK（ΑTtKΑtK）-1][ΑTtKy]。

（7）[t=t+1]，如果[t≤S]則返回第（2）步繼續迭代，如果[t>S]或殘差[rt=0]則停止迭代進入。

（8）重構得[θ]在[ΛtK]處有非零項，其值分別為最后一次迭代所得[θtK]。

輸出：信號稀疏表示系數估計[θ]

[N×1]維殘差[rS=y-ASθS]

2.2 SPWAMP算法

本文算法在SP算法的基礎上，采用弱匹配原則選取新原子，結合SAMP算法自適應思想在迭代過程中自動調整所選原子數目，并采用變步長提高信號重構精度[21]。當算法在開始執行時采用大步長快速接近（使用冪函數變步長），當接近目標時，采用小步長（步長為原步長的0.5倍），并且通過相鄰信號能量之間的關系作為改變步長的標準。

總之，基于弱選擇的稀疏度自適應回溯追蹤（SPWAMP）算法是一種結合SP算法的回溯思想和SAMP算法的自適應思想，并通過弱匹配原則選取新原子和變步長思想的新重構算法，提高了算法重構精度。

SPWAMP 算法核心步驟為：

輸入：[M×N]的傳感矩陣[A=ΦΨ]

[N×1]? 維觀測向量[y]

步長[S]

（1）初始化[r0=y，Λ0=φ，L=S，t=1]。

（2）計算[u=abs[ΑTrt-1]]（即計算[rt-1，aj]，[1jN]），選擇[u]中[L]個最大值，將這些值對應[Α]的列序號[j]構成集合[Sk]（列序號集合）;選擇[u]中大于門限[Th]的值，將這些值對應A的列序號[j]構成集合[J0]（列序號集合）。

（3）令[Ck=Λt-1？Sk？J0][Αt={aj}][（for? all? j∈Ck）]。

（4）求[y=Αtθt]的最小二乘解：[θt=argminθ||y-Αtθt||=][（ΑTtAt）-1ATty]。

（5）從[θt]的中選出絕對值最大的[L]項記為[θtL]，對應的[At]中的[L]列記為[AtL]，對應的[A]的列序號記為[ΛtL]，更新集合[F]=[ΛtL]。

（6）更新殘差，使得[rnew=y-ΑtL（ΑTtLΑtL）-1ΑTtLy]。

（7）如果[rnew≤1e-6]，則停止迭代進入，第（10）步。

（8）如果[rnew2≤rt-12]，則[Λt=F]，[rt=rnew]，[t=][t+][1]，否則進入第（9）步。

[9] 劉浩強，趙洪博，馮文全. 基于CS的正則化稀疏度變步長自適應匹配追蹤算法[J]. 北京航空航天大學學報，2017，43（10）：2109-2117.

[10] TROPP J A，GILBERT A C. Signal recovery from random measurements via orthogonal matching pursuit [J]. IEEE Transactions on Information Theory，2007，53（12）：4655-4666.

[11] WEI D， MILENKOVIC O. Subspace pursuit for Compressive Sensing signal reconstruction[J].? IEEE Transactions on Information Theory， 2009， 55（5）：2230-2249.

[12] NEEDELL D，VERSHYNIN R. Signal recovery from incomplete and inaccurate measurements via regularized orthogonal matching pursuit [J]. IEEE Journal of? Selscted Toptics in Signal Processing，2010，4（2）：310-316.

[13] DONOHO D L，TSAI G Y，STARCK J L. Sparse solution of under-determined linear equations by stage-wise orthogonal matching pursuit [J]. IEEE Transactions on Information Theory，2012，58（2）：1094-1121.

[14] DO? T? T，GAN L， NGUYEN N，et al. Sparsity adaptive matching pursuit algorithm for practical compressed sensing [C]. Piscataway：IEEE Conference on Signals，2008.

[15] 楊成，馮巍，馮輝，等. 一種壓縮采樣中的稀疏度自適應子空間追蹤算法[J]. 電子學報，2010，38（8）：1914-1917.

[16] XUE B I， CHEN X D， ZHANG Y U. Variable step size stagewise adaptive matching pursuit algorithm for image compressed sensing[C]. 2013 IEEE International Conference on Signal Processing， Communication and Computing，2013：1-4.

[17] 王烈，羅文，秦偉萌. 分段弱選擇自適應正交匹配追蹤算法[J]. 計算機工程與設計，2018，39（12）：3767-3773.

[18] 王福馳，趙志剛，劉馨月，等. 一種改進的稀疏度自適應匹配追蹤算法[J]. 計算機科學，2018，45（S1）：234-238.

[19] 王欣，張嚴心，黃志清. 基于變步長的正則化回溯自適應追蹤算法[J]. 電子學報，2018，46（8）：1829-1834.

[20] 楊韌，張興敢. 壓縮感知重構SAMP的改進算法[J]. 南京大學學報：自然科學版，2018，54（3）：538-542.

[21] 彬彬有禮的專欄. 壓縮感知重構算法之子空間追蹤（SP）[EB/OL].https：//blog.csdn.net/jbb0523.

（責任編輯：江 艷）