基于遺傳算法優(yōu)化BP神經網絡的輸水管道地基沉降預測分析

楊陽

摘 要：埋設在地下的輸水管道多應用于長距離輸水，其結構易受地基沉降影響。本文建立了神經網絡模型，并基于遺傳算法對神經網絡模型進行優(yōu)化，利用某實際工程的監(jiān)測數據，對其所產生的地基沉降值進行預測并分析，從而起到監(jiān)測預警的效果，可為同類工程提供參考。

關鍵詞：遺傳算法;BP神經網絡;地基沉降

中圖分類號：U655.5? ? ? ? ? ? 文獻標識碼：A? ? ? ? ? ? 文章編號：1006—7973（2019）05-053-02

人工神經網絡[1]具有很強的非線性擬合能力，具有很強的魯棒性、記憶能力、強大的自學能力，能對很復雜的問題、模糊且不精確的信息進行計算，而且能夠同時考慮多個因素，最終能給出較為精準的預測結果。而影響神經網絡精度的主要原因就是其權值和閾值的選取，在此處引入遺傳算法來優(yōu)化神經網絡的權值閾值，以求得到最優(yōu)解。遺傳算法[2]的思想就是利用達爾文“優(yōu)勝劣汰”的原則，選擇好的保留，不好的淘汰，最終找到全局最優(yōu)解。遺傳算法與BP神經網絡模型[3-4]相結合，可以利用遺傳算法的優(yōu)勢，解決神經網絡模型易陷入局部最優(yōu)、不易收斂等問題，從而提高了神經網絡模型結果的精度。本文將影響輸水管道地基沉降的因素輸入，利用基于遺傳算法的BP神經網絡模型，對輸水管道的地基沉降值進行預測。

1 算法簡介

1.1 BP神經網絡

BP（Back-Propagation）神經網絡[5]是一種多層前饋式神經網絡，其主要特點是：信號是前向傳播的，而誤差是反向傳播的，它是目前應用最廣泛的神經網絡。BP神經網絡模型拓撲結構一般分為三部分，分別為輸入層、隱含層、輸出層。（見圖1）。它通過對樣本進行訓練，使輸出值接近真實的期望值，從而通過誤差的反向傳播來不斷調整網絡的權值和閾值，使其誤差平方和最小。雖然BP神經網絡有結構簡單、非線性擬合能力強等優(yōu)點，但同時也存在易陷入局部極小值、收斂速度慢、“過擬合”等缺點。

1.2 遺傳算法

遺傳算法是模擬自然界中生物進化過程與機制來解決優(yōu)化問題的一種人工智能算法，它的基本思想：是按照所需求解的目標函數，設置一個適應度函數作為評價標準，再根據遺傳算法的初始化，將數據進行基因編碼從而獲得初始種群，后經過交叉變異、選擇等步驟以獲得本代適應度最好的個體。在多次迭代遺傳的過程中，通過選擇每代最好適應度的個體進行對比，最終選取最好適應度的個體，即為所求問題的最優(yōu)解。

遺傳算法的具體步驟如下：

步驟1：種群初始化：隨機生成N個個體的產生初始種群P={X1，X2，X3，…，Xn}，種群中每個個體編碼后都對應所求問題的一個初始解。

步驟2：求適應度值：個體Xi，i=1，2，3，…，n，有指定的適應度值作為評價其好壞的標準。

步驟3：選擇：根據某種策略從當前種群中選擇出M個個體作為下一代群體，選擇是按照個體的適應度值進行，淘汰適應低的個體，體現(xiàn)了進化論中自然選擇的原則。

步驟4：交叉變異：按照雜交概率PC在所選出的M個個體內隨機選出兩個個體進行交叉操作，可得到兩個新個體，該操作多次進行，直到所需雜交的個體都兩兩交叉雜交完成。在所得M個個體中，須按概率PM并根據變異規(guī)則選擇出一些個體進行個體變異操作。在交叉變異操作中，交叉操作可體現(xiàn)出個體間信息交換的思想，變異操作則是增加了種群的多樣性。

步驟5：若算法停止，解碼后得到最優(yōu)解，否則轉到步驟2重復執(zhí)行迭代運算，直至得到最優(yōu)解。

2 建立GA-BP預測模型

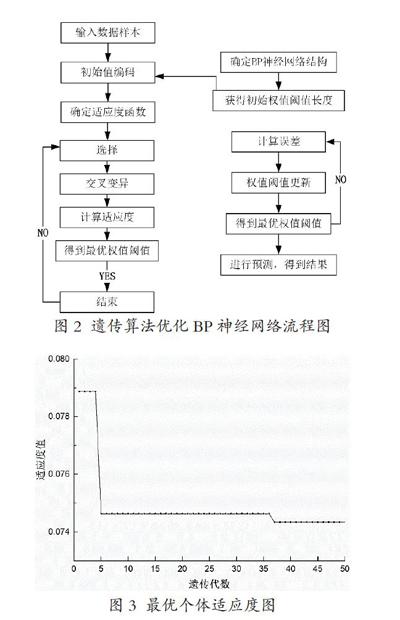
遺傳算法優(yōu)化BP神經網絡模型是用遺傳算法來進行優(yōu)化搜索，得到BP神經網絡的最優(yōu)初始權值閾值，使BP神經網絡能夠更好地進行預測輸出。本文利用MATLAB軟件來建立GA-BP神經網絡模型與BP神經網絡模型。GA-BP算法相關參數設置如下： 種群的數量為40，最大迭代次數為50，最大訓練次數為10000，訓練目標為0.01，學習速率為0.01。BP神經網絡結構為4-9-1，即輸入層4個節(jié)點，隱層9個節(jié)點和輸出層1個節(jié)點，BP神經網絡結構確定后，便可得到所需優(yōu)化的初始權值閾值的總數55。圖2為遺傳算法優(yōu)化BP神經網絡流程圖：

如圖3所示，遺傳算法的適應度值（與目標函數的誤差值）從第4代道第8代就產生了大的下降，從8代以后保持平穩(wěn)，在35代以后又出現(xiàn)了比較明顯的下降，最終收斂在0.07434。由此，易見遺傳算法對于誤差的減少起著相當顯著的作用。

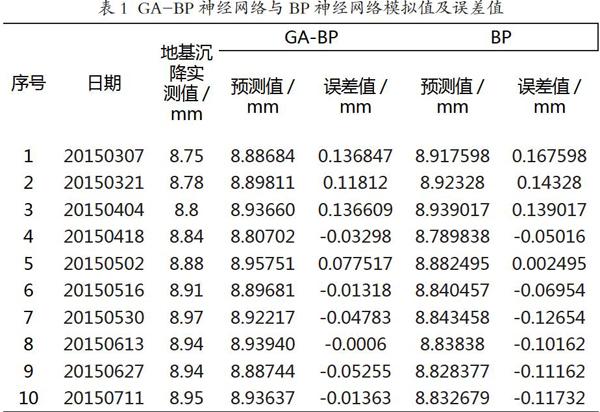
本文數據來自某段三孔箱涵的實時監(jiān)測數據，其時間為2013年1月4日到2015年2月21日，共340組數據，330組為訓練樣本，余下10組進行維數為14的滾動預測。本文選取了布置在箱涵左中右三孔的內水壓力計，以及底部的外水壓力計，溫度、時間序列作為神經網絡的輸入，地基沉降值即為所求輸出。下表是遺傳算法優(yōu)化BP神經網絡模型（GA-BP）與BP神經網絡模型模擬值與誤差值作對比分析：

由圖4、圖5可知，GA-BP神經網絡模型最大的相對誤差為0.136847，而BP神經網絡模型的最大相對誤差為0.167598， GA-BP神經網絡模型的平均相對誤差為0.0629863，BP神經網絡模型的平均相對誤差為0.102919;其次，GA-BP神經網絡模型的最大相對誤差百分比為1.563966 %，平均誤差百分比為0.713564 %，BP神經網絡模型的最大相對誤差百分比為1.915406 %，平均誤差百分比為1.16098 %。顯然，由遺傳算法優(yōu)化的BP神經網絡模型比BP神經網絡模型誤差減少且精度得到較大提高。

3 結論

（1）遺傳算法與BP神經網絡結合后，改善了BP神經網絡易受局部最優(yōu)值、過擬合等方面的影響，GA-BP神經網絡模型比BP神經網絡模型的精度得到了較大的提升。

（2）當把遺傳算法優(yōu)化BP神經網絡模型運用在地基沉降預測方面時，所得到的地基沉降值預測結果較為切合實際值，故該方法利用在地基沉降預測方面能起到良好的監(jiān)測預警作用。

參考文獻：

[1] 高浪， 謝康和. 人工神經網絡在巖土工程中的應用[J]. 土木工程學報， 2002， 35（4）：77-81.

[2] 金強國. 基于遺傳算法的大壩土石料運輸智能動態(tài)調配應用研究[D].天津大學， 2016.

[3] 李彥杰， 薛亞東， 岳磊， et al. 基于遺傳算法-BP神經網絡的深基坑變形預測[J].地下空間與工程學報， 2015， 11（s2）：741-749.

[4] 郁磊. MATLAB智能算法30個案例分析[M].北京航空航天大學出版社， 2011.

[5] 康飛. 大壩安全監(jiān)測與損傷識別的新型計算智能方法[D]. 大連理工大學， 2009.