熱環境下大范圍運動功能梯度薄板的剛-柔耦合動力學特性

王琳杰， 黎 亮， 章定國， 錢震杰

(1. 南京理工大學 理學院，南京 210094； 2. 南京農業機械化研究所，南京 210014)

航空發動機作為飛機的“心臟”，是一種高度復雜和精密的熱力機械，其葉片往往在高溫、高載的極端條件下工作，因此，航空發動機葉片在工作時可能出現斷裂、折斷、變形以及葉身磨蝕等故障，是發動機最容易發生故障的構件。波音F-18“大黃蜂”(Boeing F-18 Hornet Strike Fighter)戰斗機采用的F404發動機，其高壓壓氣機的葉片和機匣由鈦合金制作。葉片由于長時間受細小砂石的磨損導致葉片形狀發生改變從而改變了葉片的固有頻率，在氣溫300 ℃以上以及氣壓0.35 MPa以上的工況下葉片斷裂并卡在轉子葉尖與機匣之間，斷裂的葉片與機匣摩擦產生大量熱量使得鈦合金制成的葉片和機匣燃燒，最終導致飛機失事。

航空發動機葉片的結構在設計時趨向于輕、薄以滿足發動機需求，因此葉片的制作對材料要求非常之高，而傳統的材料已經無法滿足需求。功能梯度材料(Functional Gradient Materials, FGM)是性能在幾何空間上連續變化的非均質材料，比傳統材料更能夠滿足高溫、高載等極端條件，在航天航空領域具有廣泛的應用前景。熱環境對航空發動機部件的影響已經引起了工程界的高度重視，因此結合功能梯度材料建立考慮熱效應和相應結構耦合的動力學模型十分有必要。

中心剛體-柔性薄板系統是非常典型的一類剛柔耦合系統簡化模型，學者們對此類力學模型已開展了較多的研究，相關理論日漸成熟[1-10]。目前，學者們將研究方向轉移到物理場與中心剛體-柔性薄板的耦合動力學問題，其中熱耦合動力學問題尤為學者們關注[11-25]。Huang等基于高階剪切變形板理論和von Krmn方程，并考慮熱效應的影響，通過改進的攝動理論求解方程，然后分析功能梯度板的非線性頻率和動力學響應，得出溫度場和體積分數分布對功能梯度板的非線性振動和動力學響應有顯著影響。劉錦陽等用Jourdain速度變分原理以及虛功原理建立了考慮熱效應柔性板的剛柔耦合動力學方程和熱傳導方程，利用絕對節點坐標法和有限元法對系統進行離散化，然后對熱載荷所引起的和旋轉運動所引起的耦合效應以及溫度載荷對復合材料影響做了一系列的研究。Alijani等應用多模態能量法研究了熱環境中FGM矩形板的幾何非線性振動，在研究溫度和體積分數指數的影響時指出熱變形FGM板具有更強的硬化行為，體積分數指數的影響不顯著，模態的相互作用可能在熱變形的FGM板中提升，這種相互作用的提升在無變形的各向同性對應物中是不可見的。秦潔等基于薄板彎曲理論采用梁函數組合法推導出變轉速狀態下葉片頻率和振型解析解的一般表達式并分析了熱載荷作用下旋轉葉片的頻率轉向特性，但是他的研究并未涉及剛柔耦合。李清祿等基于一階剪切變形理論和哈密頓原理建立了FGM變厚度圓板在熱環境中的運動微分方程并用微分求積法計算了FGM薄板橫向振動的無量綱頻率。郝育新等基于Reddy高階剪切變形理論、Galerkin法與Hamilton原理，建立了考慮熱效應的具有二階模態的非線性運動控制微分方程，分析了面內靜態載荷對于給定參數下系統不同內共振的影響。Li等提出了一種比以往文獻中所用方法精度更高且考慮大范圍運動的FGM板動力學模型，并且研究了頻率轉向和模態耦合的現象。但他的研究沒有考慮到多物理場的耦合問題。黎亮等以做大范圍旋轉運動的中心剛體-FGM梁-集中質量系統為研究對象建立了存在溫度梯度時旋轉柔性FGM梁的動力學模型并研究了不同溫度場下FGM梁的動力學特性。雖然大量學者對功能梯度材料考慮熱效應的動力學問題進行研究，但是現有文獻中對溫度場中做大范圍運動FGM薄板的剛-柔耦合動力學模型的研究并不完善。

本文以做大范圍運動的中心剛體-FGM薄板為研究對象，在應變能中計入熱應變的影響，在一次剛柔耦合動力學理論的基礎上推導出溫度場中大范圍運動FGM薄板的剛-柔耦合動力學方程。假設功能梯度材料參數在板厚度方向按一定冪律規律分布。由穩態熱傳導方程以及泰勒級數展開法求得相應的溫度場。本文通過數值仿真對運動已知情況下大范圍運動FGM薄板進行動力學響應分析和頻率分析。

1 物理模型和幾何非線性描述

考慮熱效應的FGM薄板建模理論基于以下假設：①板的厚度相對于長、寬小得多，Kirchhoff假設成立；②板的撓度遠小于厚度，從而中面撓曲為中性面；③忽略橫向剪切變形和彎曲產生的轉動慣量的影響；④垂直于板中面的各點速度相等。

本文采取如圖1(a)所示的系統進行研究，選取圖1(b)中FGM板為研究對象，如圖1(b)所示建立混合坐標系。圖1(b)中，坐標系O-XYZ為慣性坐標系，o-xyz為浮動坐標系，平面oxy為FGM薄板中面，o-xyz坐標系三個方向的單位矢量分別為a1，a2，a3。板的長度為a，寬度為b，厚度為h，密度ρ(z)，彈性模型為E(z)，熱膨脹系數為α(z)，熱傳導系數為K(z)，泊松比為μ。變形前板中面上一點P0(x，y，0)變形后至P點，變形位移矢量為u(u1，u2，u3)。

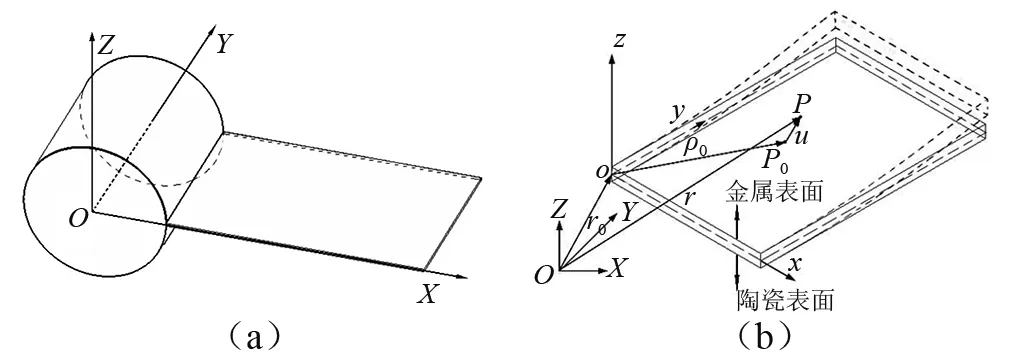
圖1 中心剛體-FGM柔性薄板模型Fig.1 Hub-FGM thin plates system undergoing large overall motion

P點在慣性基下的速度矢量VP可表示為

VP=Vo+ωA×(ρ0+u)+VPA

(1)

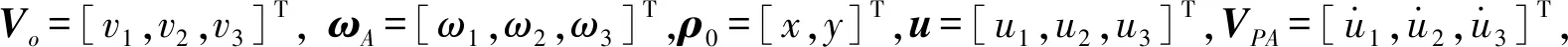
(2)

薄板上任意一點的變形位移為

(3)

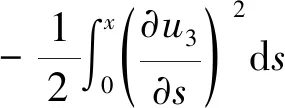
功能梯度板是由金屬和陶瓷兩種性能不同的材料組分組合而成的復合材料結構。假設功能梯度各項材料參數均為板厚方向坐標的冪函數，即

P(z)=Pm+(Pc-Pm)V(z)

(4)

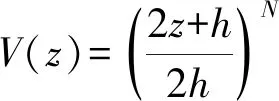
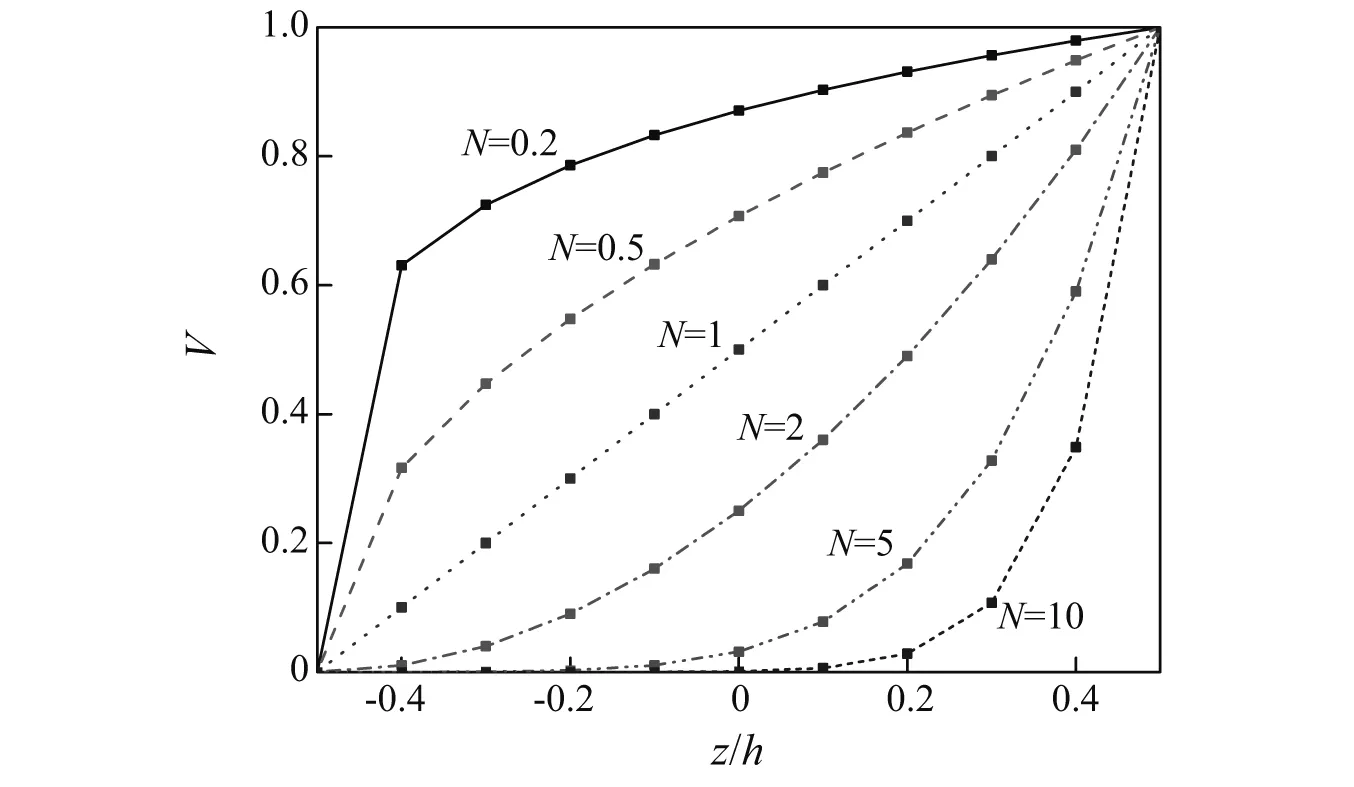
圖2 梯度材料的體積分數變化示意圖Fig.2 Volume fraction variations of gradient distribution law

假設溫度場沿著功能梯度板厚度方向梯度變化，穩態熱傳導方程的一維形式為

(5)

功能梯度板的熱邊界條件為

T(h/2)=Tc,T(-h/2)=Tm

(6)

通過泰勒級數展開求解得到功能梯度板沿厚度方向分布的溫度表達式

(7)

式中：T0為參考溫度；Tc，Tm分別為陶瓷和金屬材料界面處溫度。

(8)

2 動力學建模

系統的總動能為

(9)

FGM薄板上任意一點的應變可表示為

(10)

基于平面應力假設，FGM薄板上任意一點的應力可表示為

(11)

沿板厚度方向一點的熱應變為

(12)

式中：α(z)為FGM板的熱膨脹系數； ΔT(z)為溫度差， ΔT(z)=T(z)-T0，T(z)為沿板厚度方向任一點的溫度，溫度變化不會引起剪應變，故τxy,T=0。由本構關系可得由熱效應引起的溫度應力為

(13)

則整個系統應力-應變關系可表示為

(14)

系統的變形能可表示為

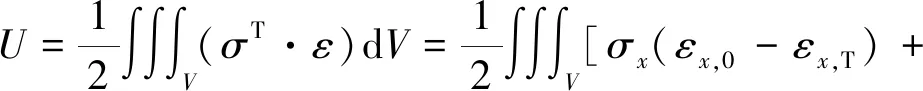
(15)

其中，

(16)

(17)

(18)

(19)

本文采用假設模態法對變形場進行離散，w1，w2，u3分別可表示為

(20)

式中：φ1(x,y)∈R1×N1，φ2(x,y)∈R1×N2和φ3(x,y)∈R1×N3分別為薄板面內振動和面外橫向振動的模態函數的行矢量；q1(t)∈RN1,q2(t)∈RN2和q3(t)∈RN3分別為面內振動和面外橫向振動的模態坐標列矢量，N1，N2，N3分別為對應的模態截斷數。為了書寫簡便，下述的表達式中省去自變量x，y，t。

將式(20)代入式(3)，得變形位移及其速度為

(21)

(22)

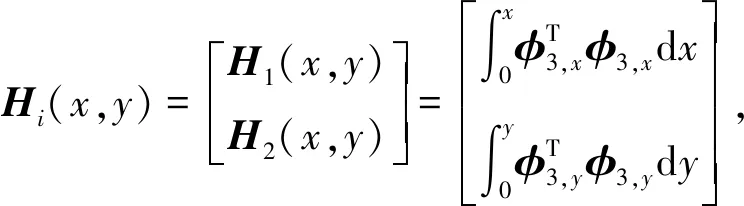
(23)

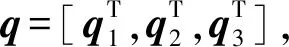
(24)

式中：各項詳見附錄。

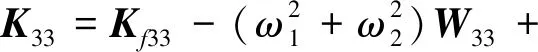
(25)

(26)

式(24)為考慮熱效應下做大范圍運動功能梯度薄板系統的一次近似剛柔耦合動力學方程。其中考慮非線性耦合變形量體現在式(25)，從式中可以看出薄板做大范圍運動的角速度、角加速度和基點o的加速度對非線性耦合量引起的附加剛度項都有一定的影響；考慮溫度效應體現在式(26)，其形式為熱效應所引起的廣義力。

3 仿真算例

3.1 FGM薄板做定軸轉動的動力學分析

以航空發動機旋轉葉片為研究對象，將其簡化為中心剛體-FGM薄板的經典模型，假設FGM柔性薄板繞y軸作定軸轉動，浮動坐標系的基點o點加速度為零，則有

(27)

僅考慮柔性薄板的面外橫向振動時，系統的動力學方程簡化為

(28)

其中,

(29)

K33=Kf33-ω2W33+ω2D11

(30)

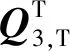
本文采用試模態函數法，將板的第m×n階模態試函數分解為x方向的懸臂梁模態函數Xm(x)和y方向自由梁模態函數Yn(y)的乘積，則FGM薄板的模態函數可表示為

φ3i=φmn=Xm(x)×Yn(y),i=1,2,3,…

(31)

式中：φ3i為式(20)中φ3的第i階分量。

x方向懸臂梁作橫向彎曲振動模態函數為

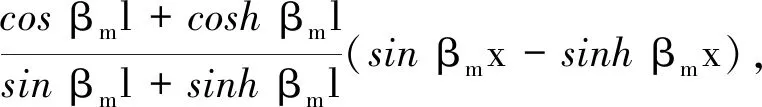
(32)

y方向自由梁作橫向彎曲振動模態函數為

(33)

式中：βm為方程cos(βml)cosh(βml)=-1的第m個根；βn為方程cos(βml)cosh(βml)=1的第n-2個根。

假設系統做大范圍轉動，運動規律設為

(34)

式中：T為剛體達到穩定轉速Ω所需時間。

本文模型選取FGM薄板參數分別為a=1 m，b=0.5 m，h=0.002 5 m，Ec=Em=70 GPa，ρc=ρm=7.5 kg/m3，αc=αm=23×10-6m/K，Kc=Km=204 W/mK，N=0，μ=0.3，模態截斷數取m=2，n=4，T=5 s，Ω=10 rad/s時，溫度邊界條件取Tc=0K，Tm=0 K，則本文選取的FGM薄板模型與Yoo等選取的均質薄板模型為同一模型。圖3中給出本文模型與Yoo等研究中模型的對比結果，從圖中可知，本文模型計算的板外側角點變形與Yoo等研究中模型計算的結果基本一致。

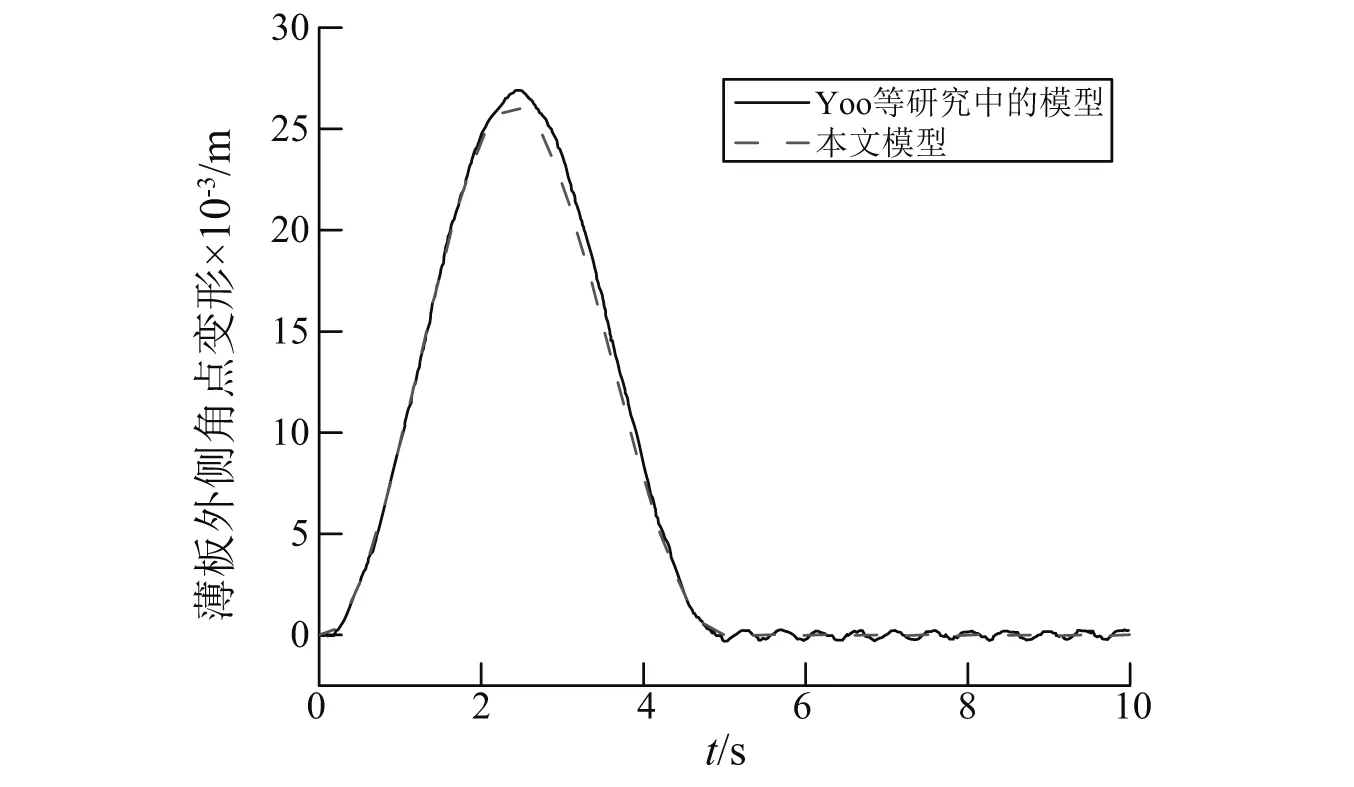
圖3 本文模型與Yoo等研究中的模型仿真結果對比Fig.3 Numerical results obtained by present model and Yoo’model

為了更好地反應在FGM薄板厚度方向呈梯度分布的溫度場對FGM薄板動力學特性的影響，現取FGM薄板參數如下：a=1.882 8 m，b=1.219 2 m，h=0.02，Ec=151 GPa ，Em=70 GPa，ρc=2 707 kg/m3，ρm=3 000 kg/m3，αc=10×10-6m/K,αm=23×10-6m/K，Kc=2.09 W/mK，Km=204 W/mK，N=1，μ=0.3，T=30 s，Ω=5 rad/s中心剛體半徑取R=0，參考溫度T0=0 K進行FGM薄板動力學分析。

圖4中給出旋轉FGM薄板在取不同模態截斷數組合時FGM薄板外側角點變形情況，從圖中可以看出，本文模型在取低階模態組合數時計算結果收斂。理論上模態截斷數選取的越高離散化的動力學方程越接近分布參數動力學方程，但是實際計算中，隨著模態截斷數選取的越高不僅計算更加復雜耗時，更會導致數值計算的發散[27]。

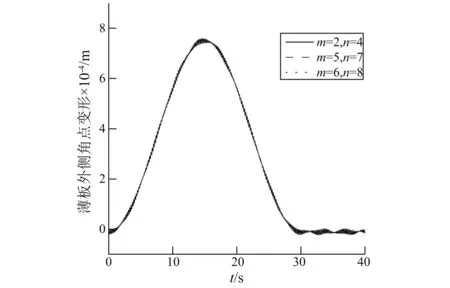
圖4 不同模態截斷數組合FGM薄板外側角點變形Fig.4 Lateral deflection of the corner point of the FGM plate in different combination of mode truncation

由傳統的材料構成的構件在溫度場中產生的熱應力非常大，往往會導致構件的損傷和失效，FGM概念的提出致力于彌補傳統材料在這一方面的不足。若取Ec=Em=70 GPa，ρc=ρm=2 707 kg/m3，αc=αm=23×10-6m/K，Kc=Km=204 W/mK，N=0，則此時FGM薄板變為均質薄板。圖5中曲線分別為體積分數指數N=1的FGM薄板和均質薄板在板上下表面溫度分別為Tc=10 K，Tm=10 K時，薄板外側角點變形示意圖以及局部放大圖。從圖中可已看出，在存在溫度梯度時，均質薄板和FGM薄板都存在振蕩現象，均質薄板振蕩現象更加劇烈，從而可以看出FGM薄板具有良好的熱應力緩和效果。

不同的溫度場對FGM板的動力學響應影響也不同，在旋轉角速度，體積分數指數N=1，參考溫度T0=0 K的條件下，選取不同溫度場對FGM薄板進行數值仿真。第一種溫度場為Tc=0 K，Tm=0 K， 此時T(z)=0 K， FGM薄板溫度不變； 第二種溫度場為Tc=10 K，Tm=10 K， 此時T(z)=10 K， FGM薄板受溫度均勻變化場影響； 第三種溫度場取為Tc=10 K，Tm=0 K，此時溫度載荷沿板厚度方向呈梯度分布，比較符合實際工況。圖6中給出三種溫度場條件下板外側角點的變形情況，從圖中可看出旋轉FGM薄板在溫度效應影響下存在一定的振蕩現象。相比于不受溫度影響，溫度均勻變化時旋轉FGM薄板振蕩現象較明顯，其原因從式(7)及式(26)可知，當不受溫度影響時Q3,T為零， 溫度均勻變化時Q3,T為定值，即廣義力項為定值，因此振蕩現象更明顯。同理，在接近實際工況的第三種溫度場下，FGM薄板外側角點變形比溫度不變時和溫度均勻變化場中大，且存在振蕩現象。

不同的邊界條件對FGM薄板的動力學響應也會有一定的影響，在旋轉角速度Ω=5 rad/s，體積分數指數N=1，參考溫度T0=0 K的條件下，選取三種不同的邊界條件，分別為：第一種溫度邊界條件為Tc=10 K,Tm=0 K； 第二種溫度邊界條件為Tc=20 K,Tm=0 K； 第三種溫度邊界條件為Tc=50 K,Tm=0 K。

圖7中給出存在三種不同溫度梯度時FGM板外側角點的變形。從圖中可以看出隨著FGM薄板上下表面溫度差的增大，FGM板變形幅值增大，振蕩也越來越劇烈。

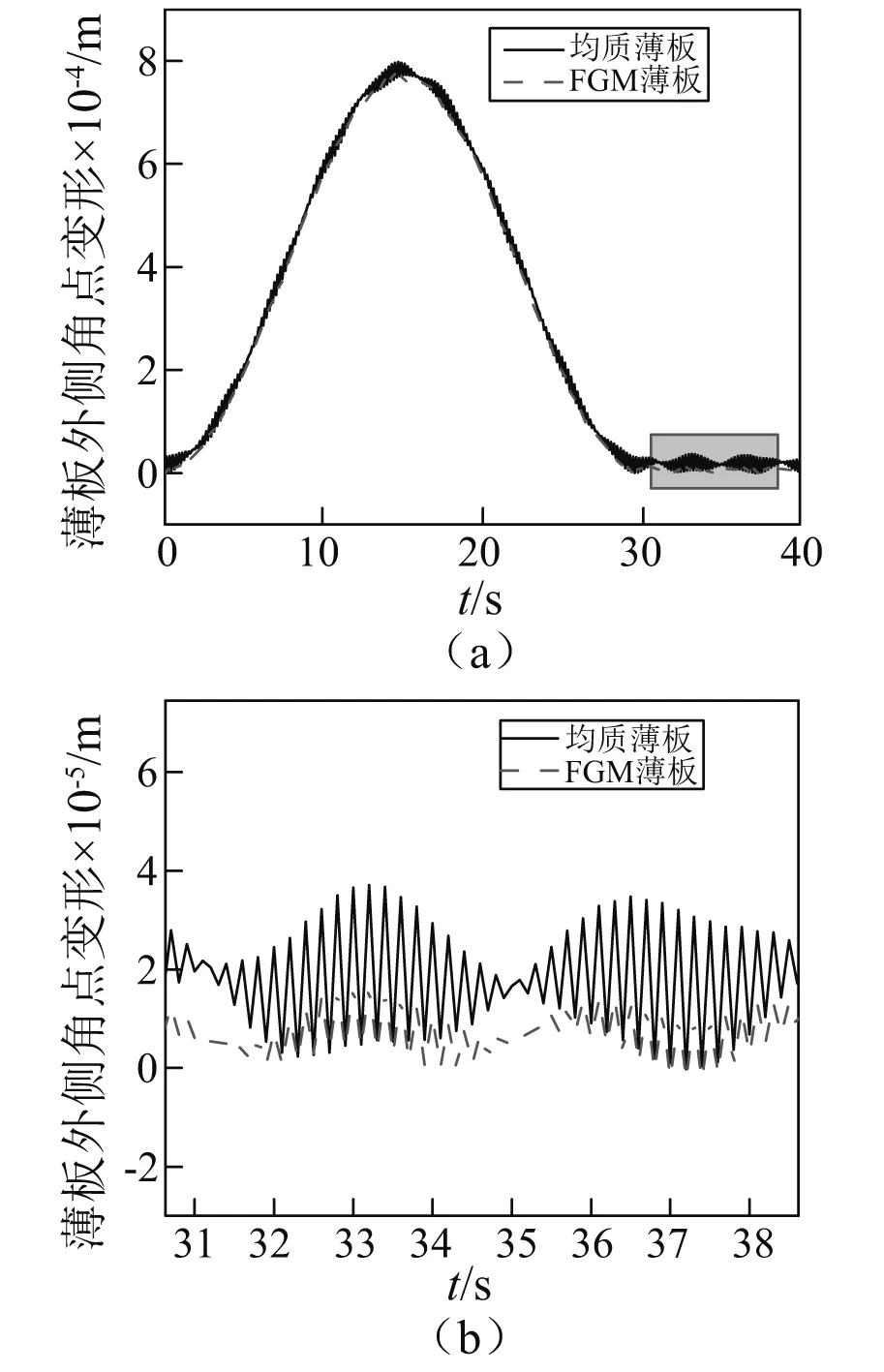
圖5 存在溫度梯度時均質薄板與FGM薄板外側角點變形Fig.5 Lateral deflection of the corner point of the homogeneous plate and the FGM plate in different temperature fields

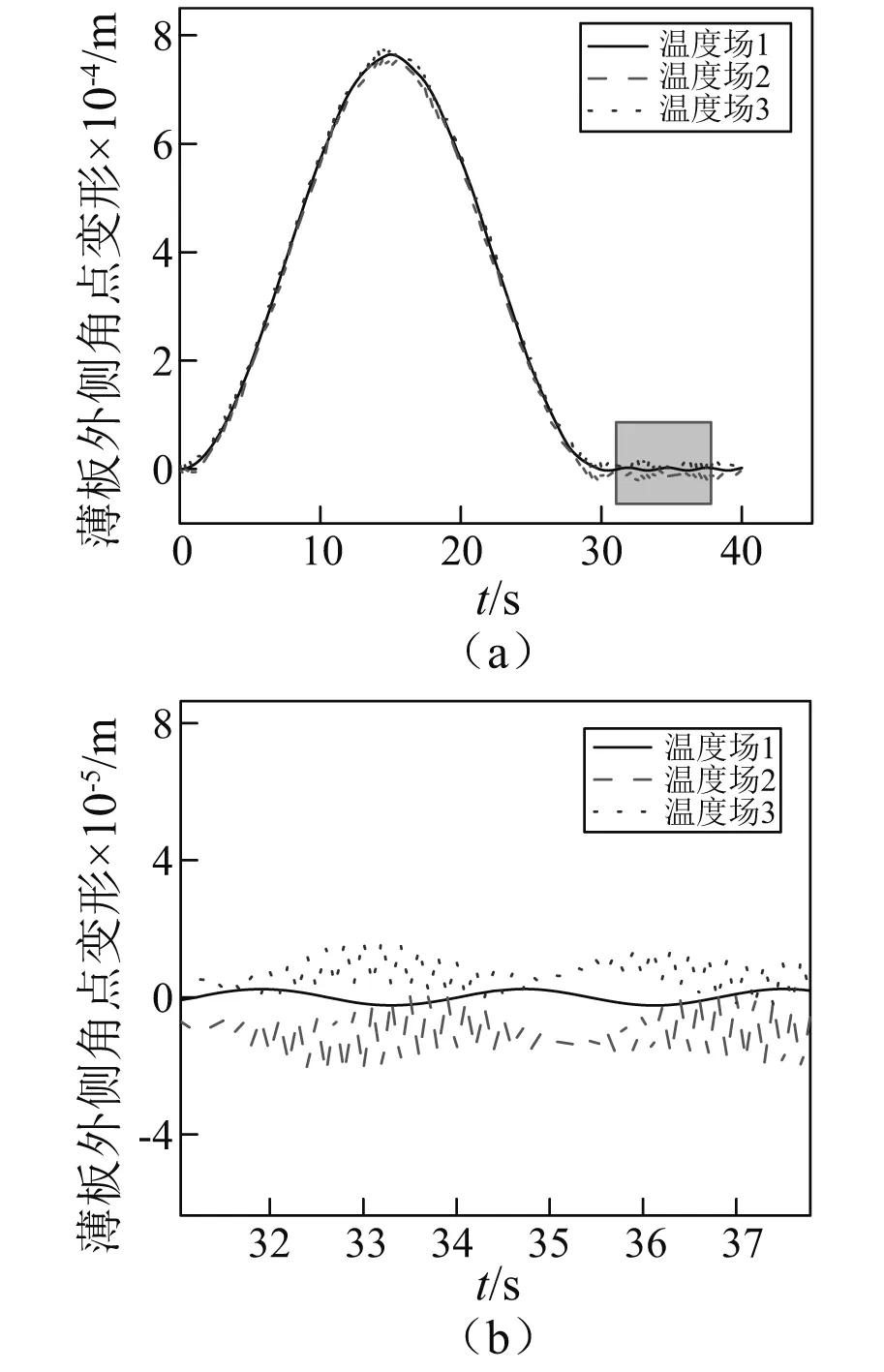
圖6 不同溫度場下旋轉FGM板外側角點變形Fig.6 Lateral deflection of the corner point of the rotating FGM plate in different temperature fields

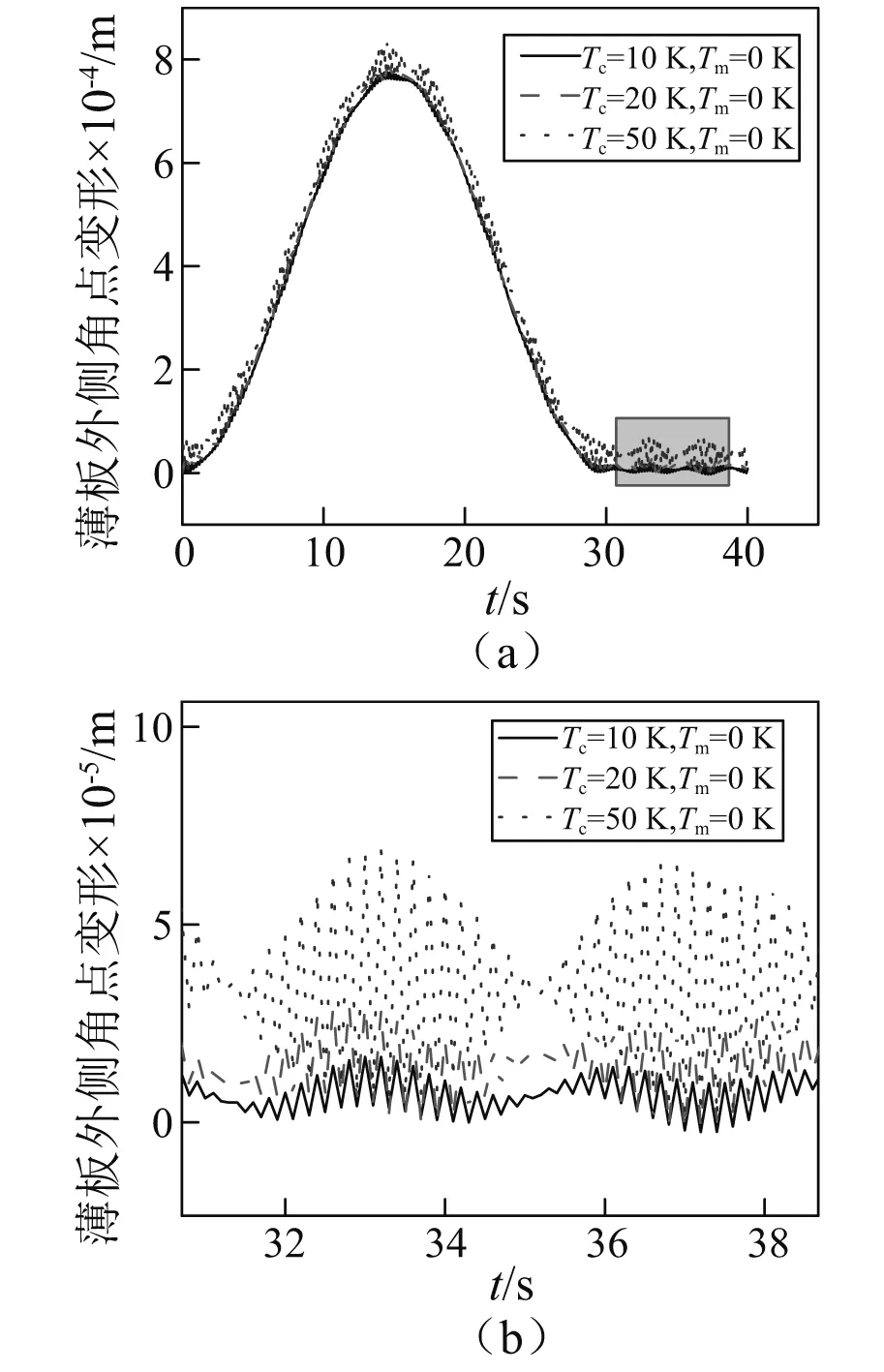
圖7 存在不同溫度梯度時旋轉板外側角點變形Fig.7 Lateral deflection of the corner point of the rotating plate in different temperature fields

當溫度場為T0=0 K,Tc=10 K,Tm=0 K時，考慮不同角速度和不同體積分數指數對板外側角點在z方向變形的影響。圖8中給出體積分數指數N=1時，對應不同角速度板外側角點的變形情況。從圖中可以看出，在溫度場影響下FGM板外側角點的變形隨著旋轉角速度的增大而增大并伴隨著輕微的振蕩現象，但是振蕩幅值變化很小。

圖9中給出旋轉角速度Ω=5 rad/s，T0=0 K,Tc=10 K,Tm=0 K時，對應不同體積分數指數板外側角點的變形情況。從圖中可知，不同體積分數指數的旋轉功能梯度薄板在存在溫度梯度時存在振蕩現象，外側角點變形與振蕩幅值隨著體積分數指數N的增大而增大。

3.2 FGM薄板做大范圍平動的動力學分析

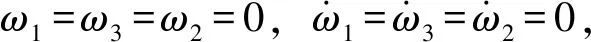
(35)

從式(35)中可以看出，FGM薄板面內方向平動加速度a01，a02對FGM薄板的剛度會有所改變，此時會發生動力剛化或者動力柔化效應。當a01C1+a02C2項為負值時，FGM薄板動力學模型剛度增大，振動頻率減增大，此時發生動力剛化效應； 當a01C1+a02C2項為正值時，FGM薄板動力學模型剛度減小，振動頻率減小，此時發生動力柔化效應。垂直于FGM薄板面的平動加速度a03對FGM薄板的廣義力有所影響，使得板的振幅改變。

FGM板的大范圍平動在不同的溫度場對動力學特性也不同，取面內加速度和垂直于板面加速度分別為a01=5 m/s2，a02=20 m/s2，a03=1 m/s2，體積分數指數為N=1，參考溫度為T0=0 K，選取不同溫度場對FGM薄板進行數值仿真。第一種溫度場為Tc=0 K，Tm=0 K，此時T(z)=0 K，FGM薄板溫度不變時；第二種溫度場為Tc=10 K，Tm=10 K，此時T(z)=10 K，FGM薄板受溫度均勻變化影響；第三種溫度場取為Tc=10 K，Tm=0 K，此時溫度載荷沿板厚度方向呈梯度分布。圖10中給出三種不同溫度場中FGM薄板做大范圍平動時板外側角點的變形示意圖，從圖中可以看出FGM薄板做大范圍平動時伴隨著強烈的振蕩現象，在恒溫場中FGM薄板變形比溫度不變時要略小，存在溫度梯度時FGM薄板變形比溫度不變時略大。

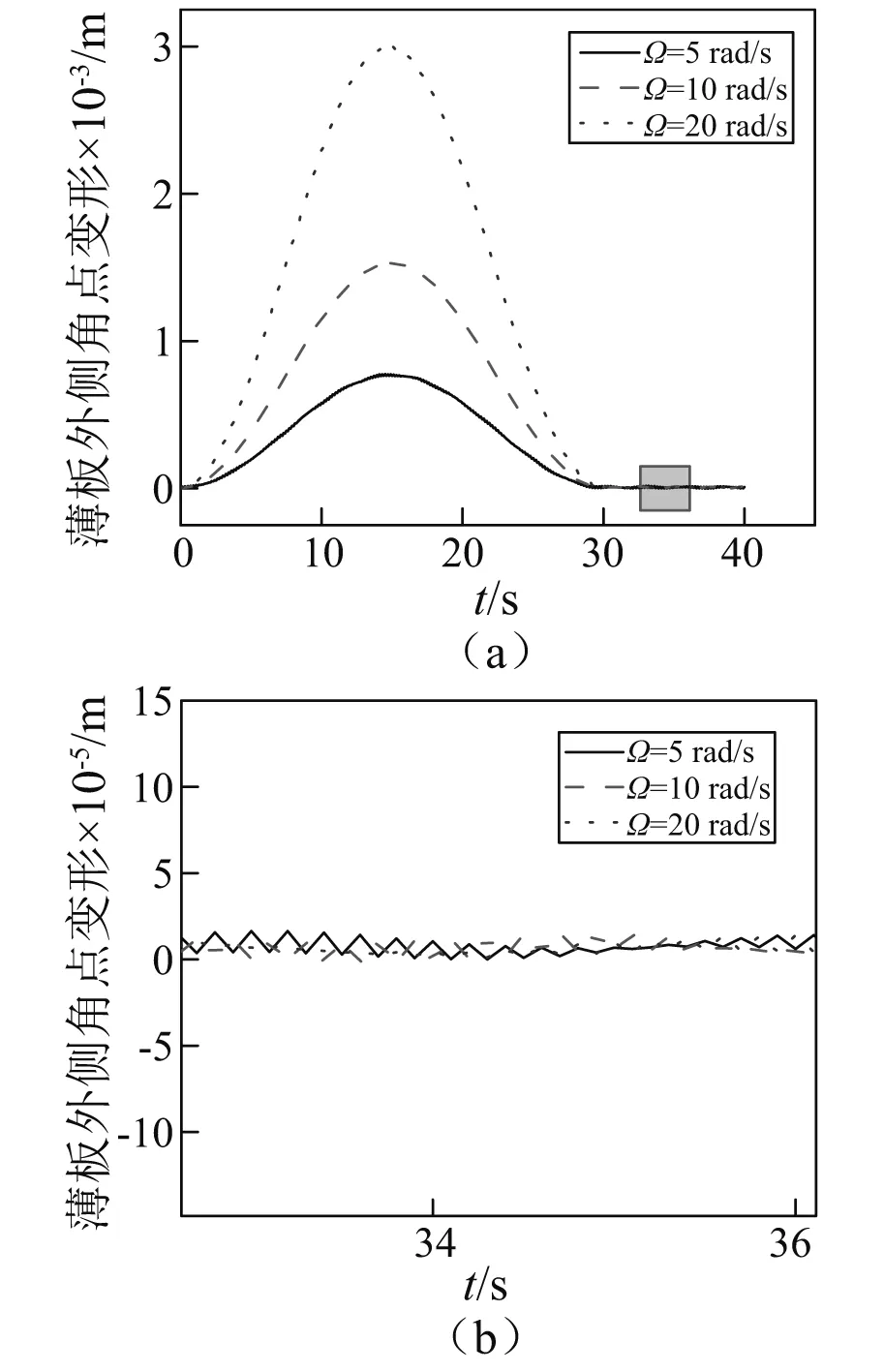
圖8 不同旋轉角速度板外側角點變形Fig.8 Lateral deflection of the corner point of the rotating plate at different angular velocities

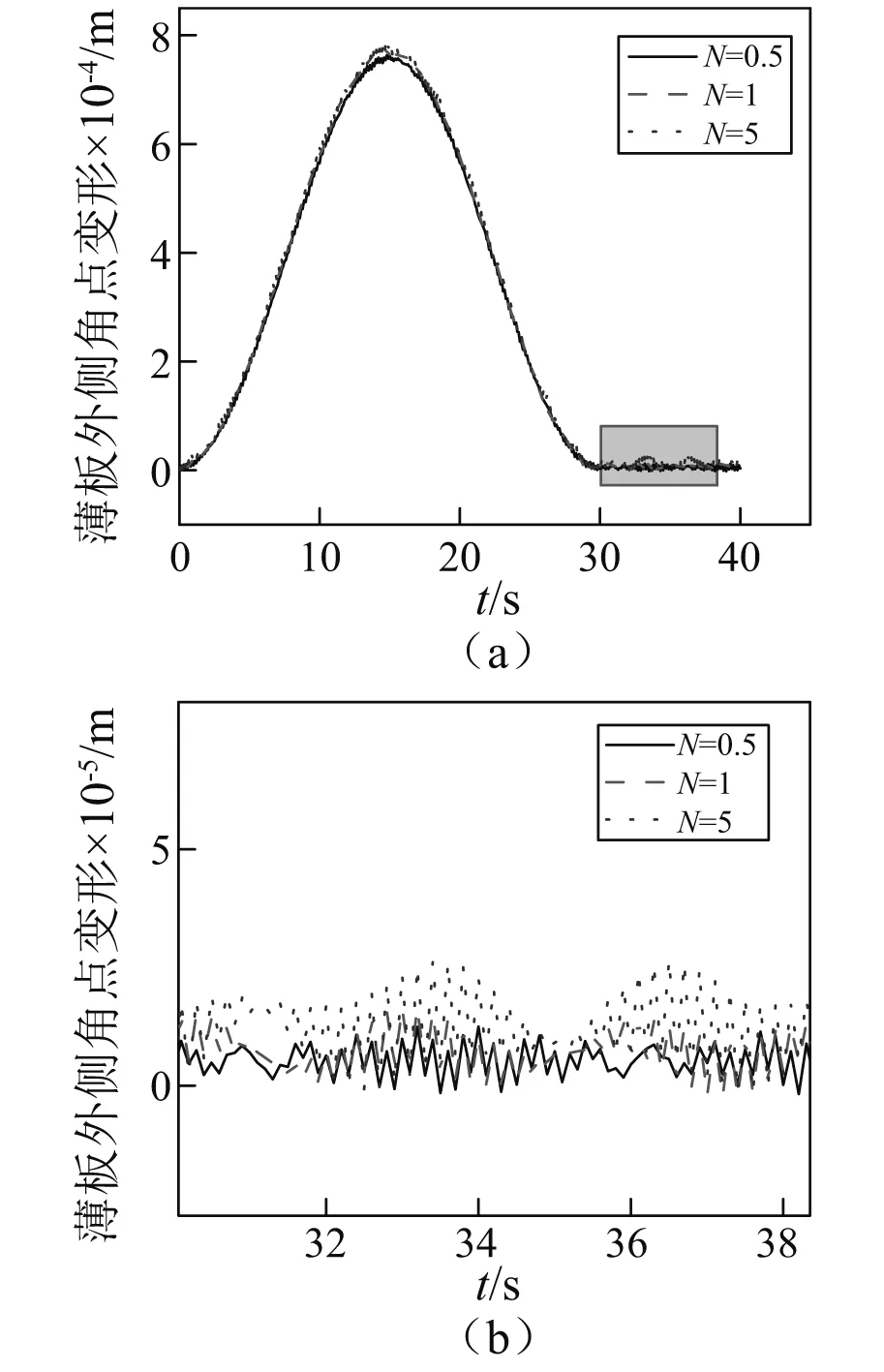
圖9 不同體積分數指數旋轉板外側角點變形Fig.9 Lateral deflection of the corner point of the rotating plate with different volume fraction exponents

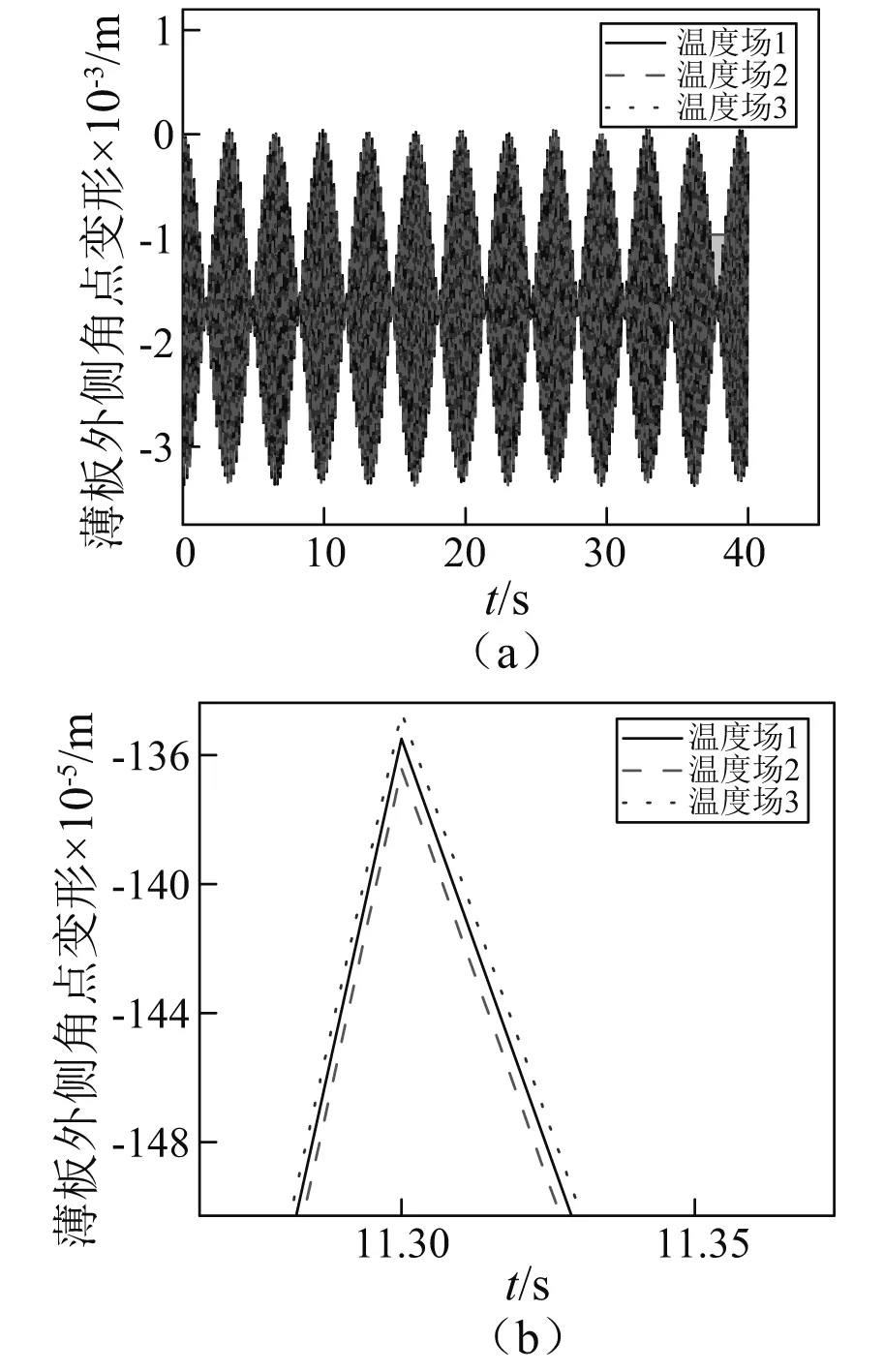
圖10 不同溫度場中平動板外側角點變形Fig.10 Lateral deflection of the corner point of the translational plate in different temperature fields

不同的溫度梯度對FGM薄板的動力學響應也會有一定的影響，取面內加速度和垂直于板面加速度分別為a01=5 m/s2，a02=20 m/s2，a03=1 m/s2，體積分數指數為N=1，參考溫度為T0=0 K，選取三種不同的溫度邊界條件，圖11中給出三種不同溫度邊界條件對應FGM板外側角點的變形。從圖中可得出隨著FGM板上下表面溫度差的增加，FGM板外側角點的變形略微增大。

選取不同的體積分數指數N對FGM薄板外側角點的變形影響也不同，選取邊界條件為Tc=10 K，Tm=0 K的溫度場，FGM薄板面內加速度與垂直于板面加速度分別為a01=5 m/s2，a02=20 m/s2，a03=1 m/s2，改變體積分數指數N的值進行數值仿真可得如圖12所示結果，從圖中可以看出，隨著體積分數指數N的增大，做大范圍平動的FGM薄板外側角點的變形幅值改變不明顯，但是其頻率會有所改變，且N<1時變化較為明顯。

3.3 FGM薄板做定軸轉動的頻率分析

給系統一繞OY軸旋轉角速度Ω，此時浮動坐標系o-xyz中原點o的速度及角速度的分量分別為

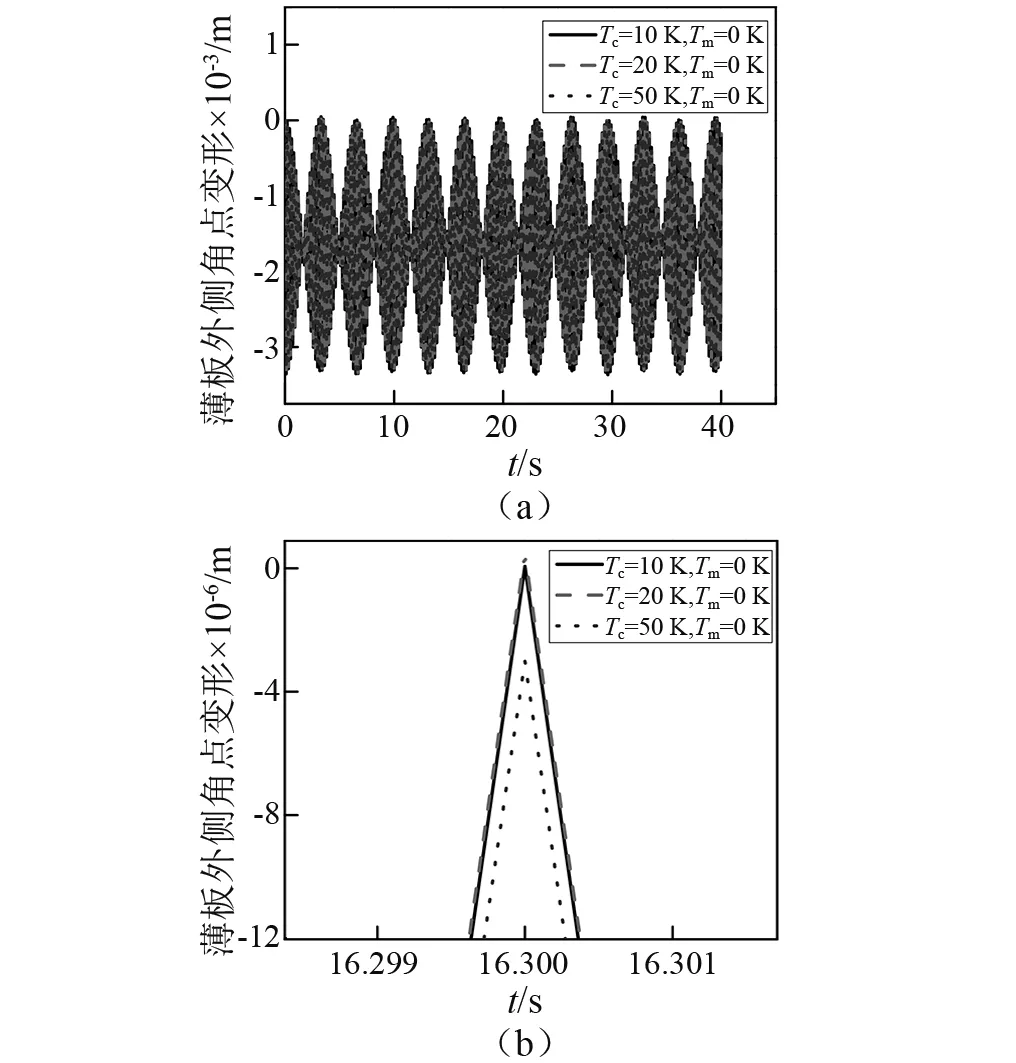
圖11 存在不同溫度梯度時平動板外側角點變形Fig.11 Lateral deflection of the corner point of the translational plate in different variable temperature fields

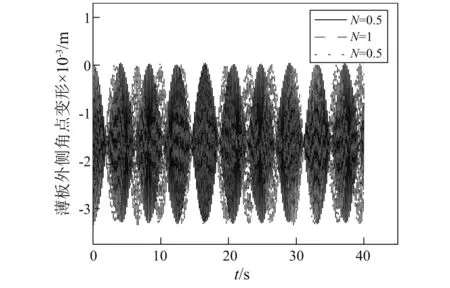
圖12 大范圍平動下對應不同體積分數指數FGM板外側角點變形示意圖Fig.12 Lateral deflection of the corner point of the translational plate with different volume fraction exponents

(36)

本文研究的柔性FGM薄板結構對動力學方程中包含的面內拉伸振動與橫向彎曲振動的耦合項忽略不計。將上式各項代入系統動力學式(24)第三行，舍去面內振動項，同時令方程右端項為零，得到旋轉FGM板的橫向自由振動方程

(37)

式中： 剛度矩陣由考慮了二次耦合變形量產生的動力剛化陣Ω2(RC1+D11)、 動力柔化項-Ω2M33以及結構動力學中的靜剛度陣Kf33三部分組成。

對式(37)進行無量綱化處理，引入如下無量綱變量

(38)

(39)

式中：D=Em/12(1-μ2);η和ε分別為FGM板中陶瓷組分與金屬組分的彈性模量比和密度比；δ為板的縱橫比；σ為中心剛體半徑與板縱向邊長之比；γ為無量綱角速度，將上述無量綱量代入式(37)可得

(40)

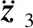
(41)

(42)

(43)

(44)

(45)

式中：ψ3為無量綱變量χ和ζ的函數， 取與φ3相同的數值；ξ為與梯度指數N有關的功能梯度材料分布系數，表示為

(46)

求解無量綱式(40)，令

z=ejωζZ

(47)

式中： j為虛數；ω為無量綱固有頻率；Z為常數列陣。將式(47)代入式(40)中得到特征值方程

(48)

求解式(48)即可獲得FGM板的無量綱固有頻率與模態振型。

由式(48)可以看出FGM板在做大范圍轉動時無量綱固有頻率與溫度不相關，為取FGM板多階頻率進行研究，現取模態截斷數分別為m=5，n=7, 體積分數指數N=1，圖13所示為無量綱固有頻率隨著無量綱角速度γ的變化的關系圖。從圖中可以看出，無量綱固有頻率隨著無量綱角速度增大而增大，并且相鄰兩階或者多階頻率之間存在頻率轉向現象或多次轉向的現象。

圖14給出不同體積分數對應的大范圍功能梯度薄板第4階無量綱頻率曲線示意圖，從圖中可以看出，隨著體積分數指數N的增大，旋轉功能梯度薄板第4階無量綱固有頻率減小。

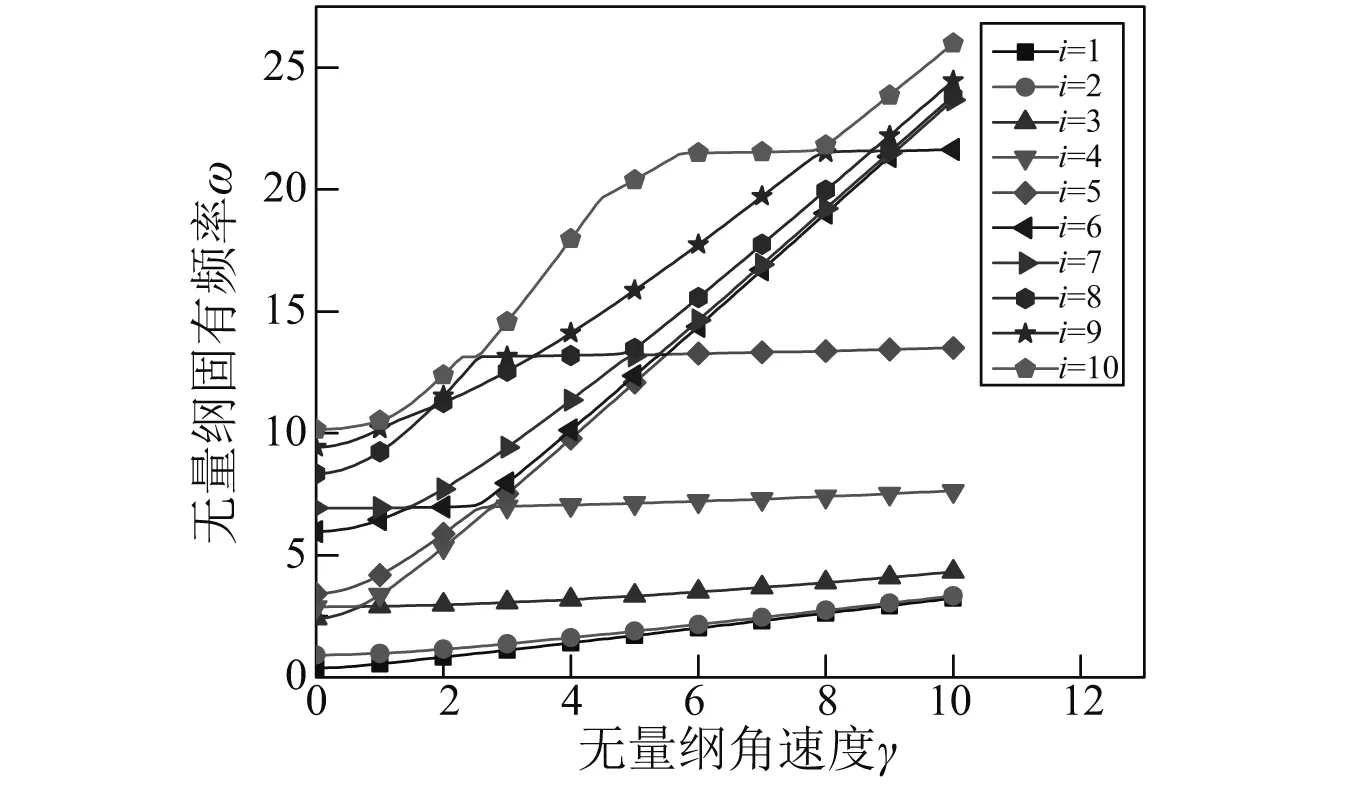
圖13 前十階無量綱固有頻率示意圖Fig.13 The first ten dimensionless natural frequencies

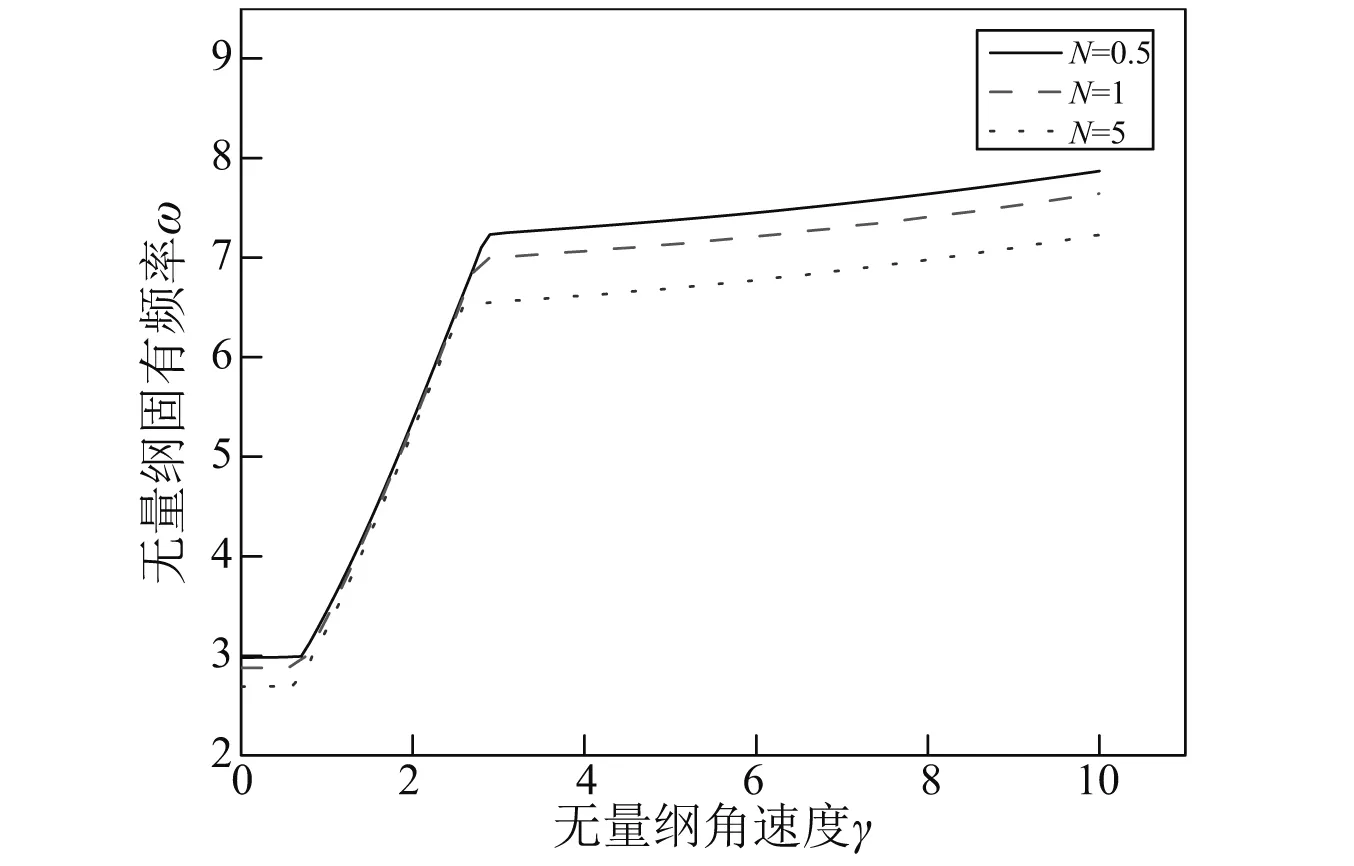
圖14 第4階固有頻率隨體積分數指數變化示意圖Fig.14 The first dimensionless natural frequencies with different volume fraction exponents

4 結 論

本文建立了存在溫度梯度時做大范圍運動FGM薄板的一次近似剛-柔耦合動力學模型，分別研究了溫度載荷和體積分數指數對大范圍運動FGM薄板的動力學響應的影響規律及振動分析等問題，得到如下結論：

(1) 存在溫度梯度時，大范圍轉動FGM薄板存在輕微振蕩幅值相對變形較小的振蕩現象，均質薄板存在較為明顯的振蕩現象，說明FGM材料有一定的熱應力緩和效果。

(2) 存在溫度梯度時，大范圍轉動的FGM薄板震蕩幅值和變形隨功能梯度薄板上下表面的溫度差增大而增大，其變形分別隨著體積分數和旋轉角速度的增大而增大。

(3) 由于動力剛化效應，做大范圍平動的FGM薄板在溫度不變、溫度均勻變化和存在溫度梯度時均存在劇烈振蕩現象，且存在溫度梯度時振蕩幅值較大。

(4) 大范圍轉動FGM薄板隨著旋轉角速度的改變往往伴隨頻率轉換現象，其無量綱固有頻率隨體積分數指數N增大而減小。