基于Apriori算法的拆零貨架儲位優化分析

李曉柯　梁玥　楊隕菽

[摘 要]現代電商物流中心雖然引進了各類智能設備，但傳統的儲位設計有待更新，智能設備與傳統儲位布局之間的沖突使得倉儲作業效率低下、成本高昂。基于Apriori算法對現代電商物流中心的儲位優化構建了簡單的關聯模型，通過挖掘的關聯規則對商品儲位進行優化，以提高倉儲中心的運作效率。

[關鍵詞]儲位優化;關聯分析;Apriori算法

[DOI]10.13939/j.cnki.zgsc.2019.27.181

1 引 言

在電子商務行業高速發展的大趨勢下，消費者的需求日益凸顯出“小批量、多品種、高頻次”的特點，由此對物流行業提出了更高的要求。為了滿足消費者個性化需求，促進電子商務的發展，在互聯網和人工智能技術的支持下，電商倉儲中心日趨“智慧化”——分揀機器人、自動導引車等先進設備的引進與使用都為倉儲作業的效率帶來了極大的提升。本文主要就電商倉儲中心拆零貨架區智能搬運機器人“貨到人”的揀選模式進行討論。在原有的儲位設計條件下，智能搬運機器人行走的路線多重復耗時，且搬運頻次較高，進而增加了倉儲作業成本。利用關聯分析可優化該區域的儲位設計，進一步提高倉儲作業的效率，降低倉儲作業成本，同時有利于提高消費者響應速度。

2 方法介紹

2.1 關聯規則

關聯規則是形如X→Y的蘊含式，是在同一件事物出現不同項的一種關系。

定義1：設I=（i1，i2…，ik），是項目集合，D=（t1，t2，…，tk）為事物數據庫，其中每個事物（Transaction）t是I的非空子集，即tI，且每一個事物都與一個唯一的標識符TID（Transaction ID）對應。因此關聯規則可以表示為X→Y的邏輯蘊涵式，其中XI，YI，且X∩Y=。

定義2：關聯規則X→Y支持度（Support）是事物數據庫中包含X∪Y的事物占事物數據庫D的百分比，即P（X∪Y）;關聯規則X→Y置信度（Confidence）是事物數據庫中包含X事物同時包含Y事物占事物數據庫的百分比，即P（Y∣X）。即

Support（X→Y）=P（X∪Y）

Confidence（X→Y）=P（Y∣X）

支持度代表了規則的出現頻次，而置信度代表了規則是否重要的可靠程度。在挖掘關聯規則時通常會設定支持度和置信度的閾值，即最小支持度（min_support）和最小置信度（min_confidence），當同時滿足支持度和置信度的閾值時，則稱該關聯規則為強關聯規則，即該關聯規則是有價值的。

2.2 關聯規則挖掘

2.2.1 高頻項目組

高頻項目組指某一項目組發生的頻率在事物數據庫中達到某一水平，即滿足最小支持度。滿足最小支持度的稱為高頻k-項目組。算法將從高頻k-項目組中再產生（k+1）-項目組，直到無法再找到更長的高頻項目組為止。

2.2.2 產生關聯規則

在高頻k-項目組的基礎之上產生關聯規則，若一個規則達到置信度閾值，即滿足最小置信度，則稱此規則為關聯規則。

2.3 Apriori原理

Apriori（拉丁語“來自以前”）算法是典型用于挖掘關聯規則的頻繁項集算法，是由R Agrawal和R Srikant于1994年提出的為布爾關聯規則挖掘頻繁項集的原創性算法。

Apriori算法的核心思想是利用頻繁項集的先驗性質（Prior Knowledge）或稱頻繁項集的反單調性，即頻繁項集的非空子集一定是頻繁的，通過逐層搜索的迭代方法尋找頻繁項集，即將k-項集用于探索（k+1）-項集，以此窮盡數據集中的所有頻繁項集。首先計算1-項集中的候選集C1，即候選1-項集，從C1中找出頻繁1-項集L1;根據頻繁1-項集計算候選2-項集C2，從C2中找出頻繁2-項集L2，…，依次迭代，直到某個k值使得頻繁k-項集為空時停止。每找一個頻繁項集LK都需要掃描一次數據庫，Apriori算法通過前述的先驗性質來減緩搜索的速度。

2.4 Apriori算法偽代碼

整個Apriori算法的偽代碼如下：

當集合中項的個數大于0時

構建一個k個項目組成的候選項集列表

檢查數據以確認每個項目都是頻繁的

保留頻繁項集并構建k+1項組成的候選項集列表

數據集掃描的偽代碼如下：

對數據集中的每條交易記錄tran

對每個候選項集can

檢查一下can是否是tran的子集：

如果是，則增加can的計數值

對每個候選項集：

如果其支持度不低于最小值，則保留該項集

返回所有頻繁項集列表

3 算例分析

本算例主要用于優化在小件拆零揀選區中的儲位設計，利用Apriori算法對訂單進行相關分析，挖掘其中蘊含的關聯規則，從而對商品儲位進行優化。為簡化算例過程，此處僅分析兩種商品之間的關聯關系。

某電商物流中心一周內的歷史有效訂單共3344條，其中包括8種品類。本算例選取其中的休閑食品為代表展開相關分析。

如表1所示，在休閑食品品類中的27種商品一周內的有效訂單情況，此處設置最小支持度（min_supprot）=0.03，最小置信度（min_confidence）=0.4，同時為了簡化計算演示過程，此處只討論頻繁2-項集情況。由于考慮到數據較為復雜，數據量較大，這里借助Python語言環境實現對關聯規則的挖掘。

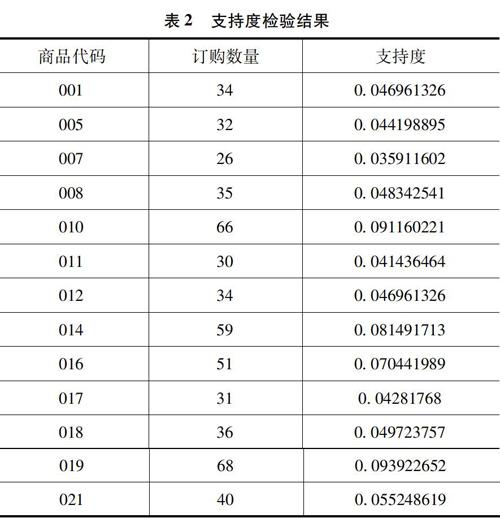
在最小支持度為0.03的條件下，得到表2中13種滿足要求的商品，即頻繁1-項集（L1）。又對這些商品重新命名為X1，X2，…，X13，生成候選2-項集（C2），在此基礎之上產生頻繁2-項集（L2）。

由此根據算法結果分析應把表3所述的幾種商品存儲在同一小件拆零貨架，以此減少智能搬運機器人行走路線重復的概率，提升分揀搬運效率，降低倉儲作業成本。

有時某些商品盡管被訂購的頻率較高，但數量很少，還應對關聯分析模型進行優化，即加入數量權重，使挖掘出的關聯規則更有價值。但此處為簡化討論，暫不將數量權重考慮其中，僅討論簡單關聯規則下對儲位進行優化的策略。

4 結 論

本文基于Apriori算法對電商物流中心小件拆零區的儲位進行優化設計，以此配合智能設備的高效運作。根據商品的關聯規則，重新安排儲位，提高倉儲作業的效率，降低運營成本，更能提高對于消費者需求的響應速度。本文所構建的模型較為簡單，雖然在Python構建了Apriori算法，但由于數據量較大，程序運行速度較慢，后期還可以改進為使用FP-growth算法來提升尋找頻繁項集的效率，處理更大的數據量。同時優化模型加入數量權重，使得簡單的關聯規則更有現實意義和價值。

參考文獻：

[1]崔妍，包志強.關聯規則挖掘綜述[J].計算機應用研究，2016，33（2）：330-334.

[2]段玉曉.基于Apriori關聯規則的信息技術相關股票數據分析[J].科技經濟導刊，2018，26（31）.

[3]張志勇，張新輝，劉杰.基于Apriori算法的關聯規則挖掘在配送中心儲位規劃中的應用[J].物流工程與管理，2012，34（4）：56-59.