一種記憶區間蟻群算法及其仿真分析*

劉 振 王亞蛟

（1.海軍航空大學岸防兵學院 煙臺 264001）（2.92706部隊 寧波 315813）

1 引言

蟻群優化算法作為一種經典的啟發式智能優化算法，由Dorigo M率先提出［1]，經過二十多年的發展，已經廣泛應用于故障診斷［2]、路徑規劃［3]、圖像處理［4]、網址追蹤［5]等問題。由于基本蟻群容易陷入局部極值并且收斂速度慢，國內外已經有許多學者提出了很多改進的蟻群算法，例如小生境蟻群算法［6]、協同進化蟻群算法［7]等，文獻［8]提出一種改進蟻群算法用于網絡編碼資源最小化問題，基于特定問題設定啟發式信息，同時提出一種多維信息素保留體制，文獻［9]將蟻群算法與迭代局部搜索算法相結合。雖然已經有諸多學者對蟻群算法進行了改進，并有效提高了蟻群算法的收斂性能，但蟻群算法作為一種仿生智能進化算法，由于其迭代尋優過程的本質特點，導致其收斂速度和收斂性能方面仍然受到一定的限制。

從當前諸多改進方法可以看出，要想提高蟻群進化算法的優化性能，在保留螞蟻的尋優特點以及整體優化流程的基礎上，必須從螞蟻路徑選擇方式和信息素更新方式出發對算法進行相應改進和推廣。綜合以上的分析和考慮，本文提出了一種轉移概率為區間概率，并且信息素更新方式具有記憶特征的記憶區間蟻群算法（memory interval ant colony optimization，MIACO），將蟻群算法的信息素濃度推廣為區間數，并對螞蟻路徑的概率選擇方式進行了有效的改進，同時結合人類記憶特征［10]，對螞蟻信息素的更新方式進行了擴展。

2 基本蟻群算法及其存在的問題

對于一個具有n個城市的TSP問題，共有n只螞蟻進行迭代尋優，當第k只螞蟻處于第i個城市時，其選擇下一個城市的訪問概率可以表示為

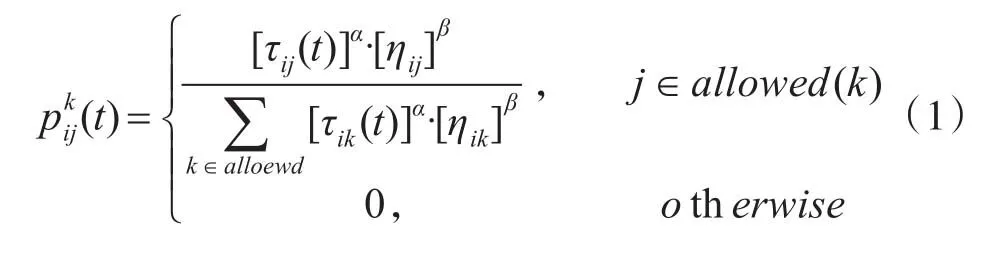
在式（1）中，τij為第i個城市和第j個城市之間的信息素濃度，ηij表示路徑長度的啟發式信息，dij表示城市之間的距離，α和β分別為信息素濃度和啟發式信息的重要度影響因子，allowed(k)為第k只螞蟻的下一步允許經過的路徑集合。螞蟻根據式（1）進行迭代搜索，當經過一定的迭代次數以后，完成一次遍歷搜索，更新經過的每條邊的信息素濃度，更新方法按式（2）進行。

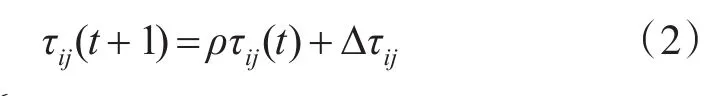
從基本蟻群算法的進化過程可以看出，每只螞蟻都以固定概率的選擇下一個節點，勢必存在一定的缺陷。首先信息素濃度和啟發式信息都是固定的數值，選擇方式較為單調，為提高選擇過程中的多樣性，可考慮采用區間參數信息和區間概率的選擇方式，能夠保證在選擇較優路徑的基礎上，增加尋優過程中的隨機性。其次螞蟻都傾向于選擇最優路徑，因而信息素濃度容易累積在局部路徑上，限制了尋優能力較強的螞蟻的全局選優能力，不能充分協同利用蟻群優化算法的勘探（exploration）和開采（exploitation）能力，可考慮對路徑的更新范圍推廣到次優路徑，并對全局更新和局部更新采用基于人類記憶的更新方式。

3 記憶區間蟻群算法的提出

3.1 區間信息素濃度的初始化方法

在以往的蟻群進化算法中，在初始時刻，都是采用統一的信息素濃度，沒有體現出啟發式信息指導作用，因此為了提高算法的收斂性能，在算法初始化的過程中，提出區間信息素濃度為區間數的方法，其設置方法如式（3）所示：

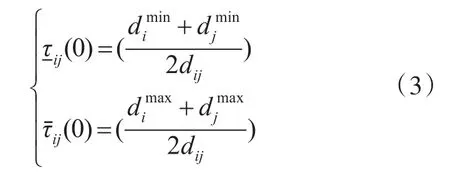
3.2 區間概率的轉移方法

當信息素濃度為區間數時，蟻群的轉移概率也為區間概率形式，選擇某一節點j的概率上限為

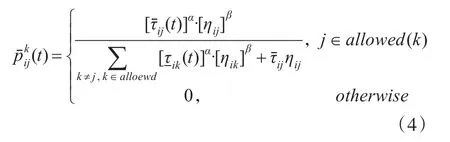
選擇某一節點j的概率下限可以表示為

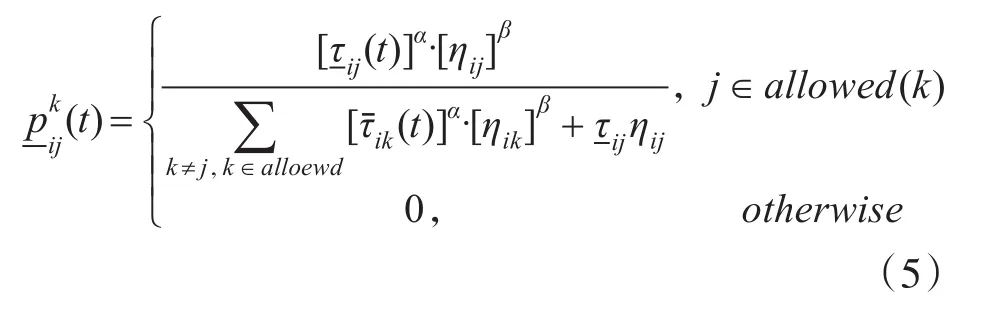
當得到某一節點概率區間以后，利用最大熵［11]方法得到精確的點概率。對于概率可按照式（6）求解最優化模型，獲得點概率值：

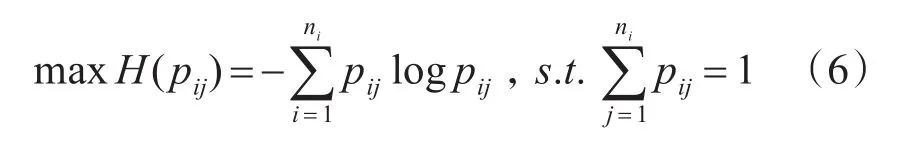
3.3 區間信息素濃度的更新方法

按照認知心理學的界定，人類記憶的特點分為長時記憶、短時記憶和瞬時記憶［12]。不失一般性，本文只考慮長時記憶和短時記憶對信息素更新的影響。蟻群算法中信息素的更新方式有效地融合人類記憶的特性，對于全局最優路徑及其部分次優路徑，將其歸入長時記憶的范疇，即記憶較為深刻的信息素，短時記憶在人類記憶方式中對應印象并不深刻的事物，在蟻群算法中，對應于一次尋優后得到的可行路徑。

螞蟻尋優過程中的信息素按照不同記憶方式，分為長時記憶更新方式和短時記憶更新方式，分別設置長時記憶因子系數和長時記憶揮發系數，短時記憶因子系數和短時記憶揮發系數。采用基于長時記憶的更新方式，對一次迭代完成后的最優路徑及其次優路徑的信息素進行全局更新，而在短時記憶方式中，則利用短時記憶因子系數和短時記憶揮發系數對相應路徑及其次優路徑信息素進行局部更新。

3.3.1 信息素的全局記憶更新方式

信息素更新方式對提高蟻群算法的全局收斂性能具有重要的作用，但通過蟻群算法信息素的更新方式可以看出，利用這種正反饋機制，有效增加了全局最優解信息素濃度的同時，也使得最優解和其它解之間的信息素濃度差距變大。在蟻群尋優過程中，次優解中的路徑片段往往是潛在最優解的部分路徑片段，因此為提高算法的收斂精度和收斂速度，本文提出除了更新當前最優路徑以外，同時更新適應度較優的若干次優路徑，提高進化過程中螞蟻選擇的多樣性。

假定此時的最優路徑值為fb，判斷當前路徑是否滿足：

當路徑滿足式（7）時，則對該路徑進行一次全局記憶更新。引入長時記憶因子系數λL，長時揮發系數ρL，此時的信息素濃度選擇使用區間數的上限進行更新，即按照式（8）進行更新：

其中

3.3.2 信息素局部記憶更新方式

當螞蟻經過的路徑并非最優路徑時，將其視為短時記憶路徑。基本蟻群算法路徑更新和選擇方式的優點在于簡單易行，收斂速度較快，但收斂的時間過長并且收斂效果并不優越，無法保證取得全局最優結果。因此針對基本蟻群算法存在的問題，將所有的路徑進行排序，當t時刻處于節點i的某只螞蟻按照式（1）選擇某個節點j后，按照式（9）更新信息素濃度：

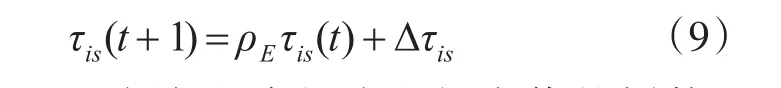
在式（9）中，Δτis為該段路徑片段長度值的倒數，為短時記憶因子系數，ρE為短時記憶揮發系數。若路徑Lij為節點i與相鄰結點之間的最短路徑，假定此時的次優路徑為Lik，則按照式（9）更新信息素τik(t+1)，若路徑Lij并不是節點i與下一節點之間的最短路徑，假定此時的最優路徑為Lih，則更新路徑τih(t+1)。

通過上述的描述，可以總結本文提出的記憶區間蟻群算法（MIACO）的步驟如下。

步驟1初始化算法的參數信息，包括蟻群的規模，算法的循環迭代次數，按照式（3）初始化信息素濃度，以及α、β、λL、ρL、λE及ρE等參數；

步驟2判斷是否滿足結束條件，不滿足則繼續循環迭代，即t←t+1；

步驟3依據區間概率的方式，獲得螞蟻選擇下一結點的區間概率其中概率的計算可按照式（4）和（5）；

步驟4依照式（6）獲得選擇概率的點概率值pij，第k只螞蟻依據pij選擇下一結點；

步驟5在完成一步行進后，將其標記為短時記憶，按照式（9）進行局部信息素更新；

步驟6當所有螞蟻都完成一次遍歷后，根據式（7）選擇符合長時記憶更新方式的候選路徑集合，并按照式（8）進行更新；

步驟7判斷是否滿足迭代結束條件，滿足則結束，輸出最優解，否則轉步驟2。

4 記憶區間蟻群算法收斂性分析

定義1：

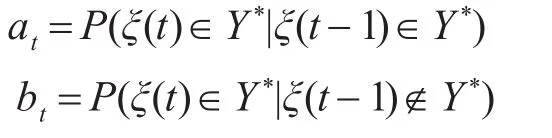
定理1：若滿足：

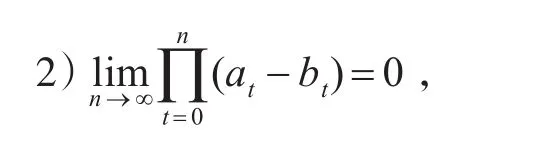
證明：

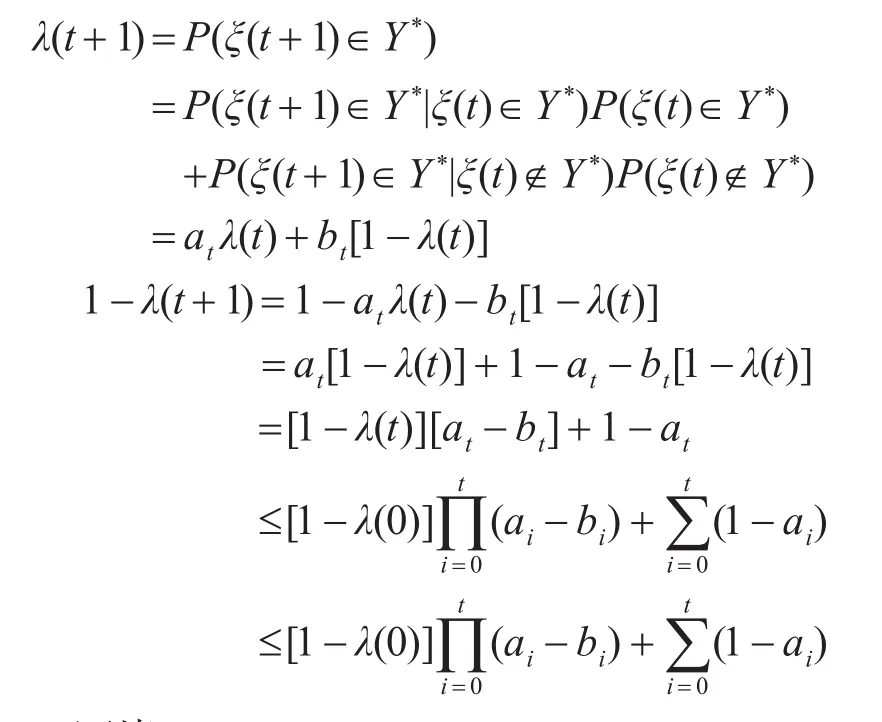
證畢。

5 記憶區間蟻群算法仿真驗證分析

為了充分驗證算法的有效性，對算法利用TSP問題進行仿真分析，設定α=1，β=1.5，ε=0.95，λL=1.2，ρL=0.90，λE=1.1，ρE=0.80，參數Q隨問題規模自適應調整為了驗證算法的有效性，選用五個典型的TSP問題進行仿真分析，分別是Fri26、Bays29、Eil76、KroD100及Eil101進行仿真分析。算法獨立運行十次，將本文提出的記憶區間蟻群算法（MIACO）與基本蟻群算法進行仿真對比，統計結果如表1所示。

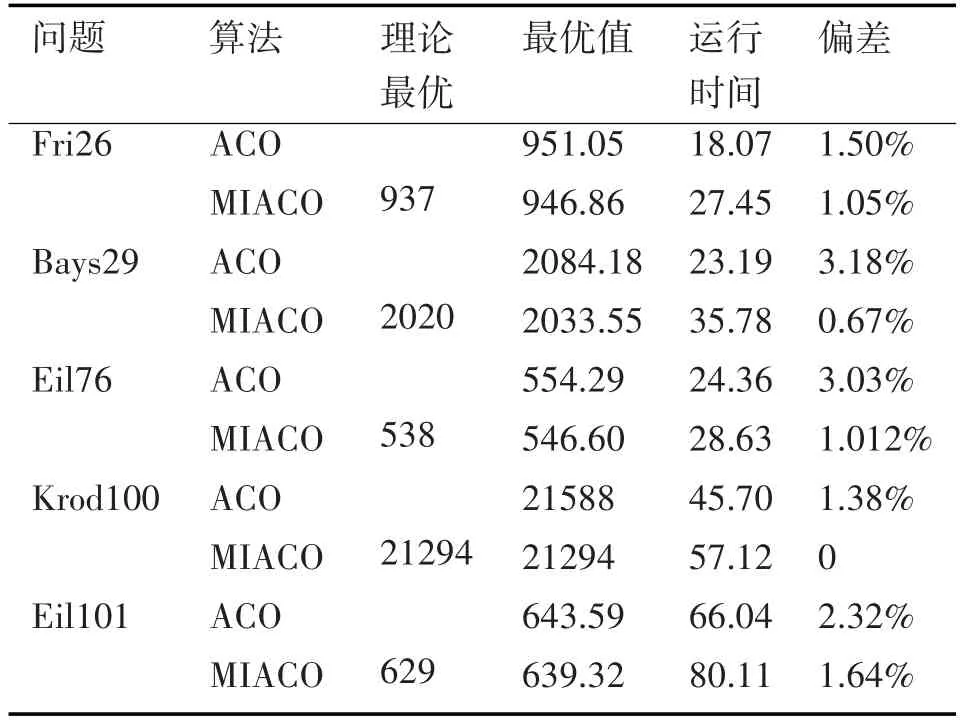
表1 TSP問題仿真結果對比

從統計結果可以看出，本文所提出的MIACO在幾個典型TSP問題中都能取得較好的尋優結果，并且在某些函數能夠獲得理論最優值，而這在很多情況下傳統ACO算法所無法達到的。但同時也注意到，本文算法的運行時間較之以前有了較為明顯的增加，特別是當TSP問題的規模在不斷擴大的時候。這主要是因為隨著問題規模的不斷增大，采用區間數進行路徑更新以及利用區間概率選擇路徑時，問題的規模急劇變大，在增加選擇多樣性的同時，也增加了系統的負擔，加重了系統的開銷。因此本文提出的MIACO，在優化規模較小的TSP問題時，可以在計算精度和計算效率之間得到較好的平衡，當問題規模較大時，可以適當將信息素的更新方式采用傳統的點概率更新方式。

為了進一步進行對比分析，將Bays29和Eil101進行仿真對比分析，收斂迭代結果分別如圖1和圖2所示。

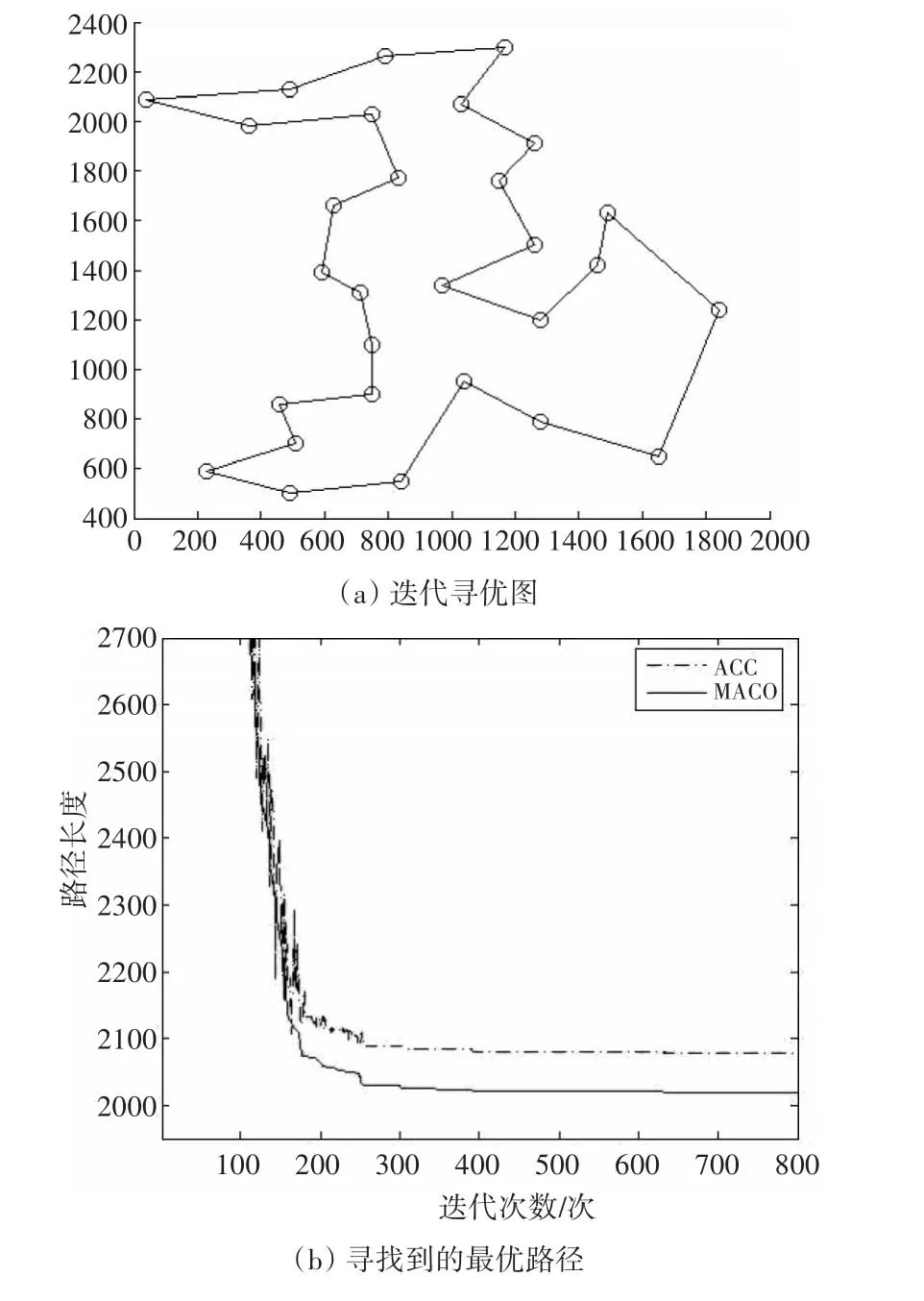
圖1 Bays29問題仿真對比結果

從圖1和圖2可以看出，利用本文所提出的MIACO，無論是取得的最優解，還是最終解的穩定性都較基本ACO有了明顯的進步，顯示出本文利用區間概率選擇路徑和信息素記憶更新方式體現出的優越性。

為進一步進行分析，以Oliver30及Eil51問題為例，將本文算法與相關文獻比較，MIACO運行的結果優于大部分文獻的方法，只有文獻［15]的方法所尋找到的最優值略優于本文提出的方法，但算法穩定性并不如本文算法。

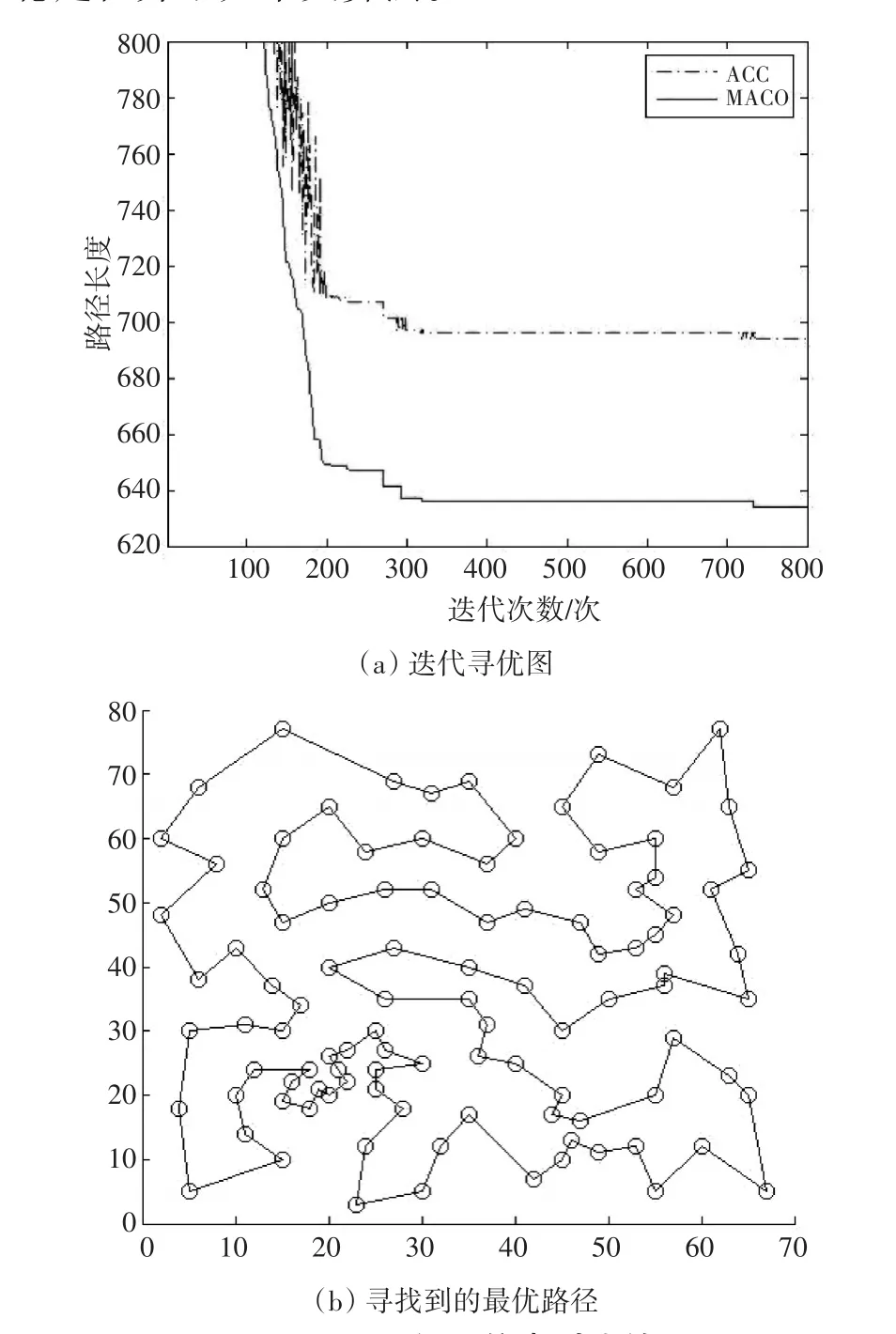
圖2 Eil101問題仿真對比結果

表2 Oliver30問題對比表

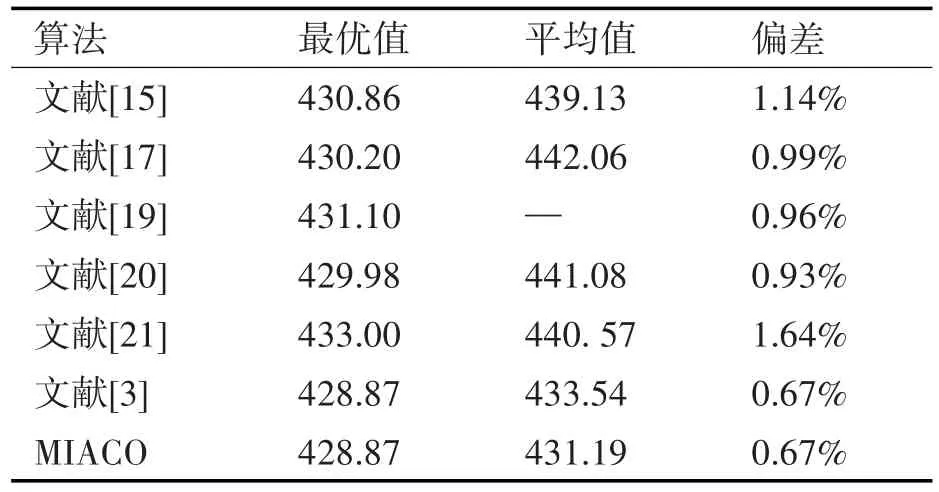
表3 Eil51問題對比表

由表2和表3的對比結果可以看到，利用本文提出的MIACO算法，在求解Oliver30以及Eil51上都已經具備了良好的性能，其性能較文獻［3]也更為穩定，充分顯示出MIACO的優越性。

6 結語

本文提出一種具有記憶特征的區間蟻群優化算法MIACO。算法的最主要的特征在于將信息素濃度推廣到區間數，打破了過去信息素濃度都為固定數值的局限性。在路徑的揮發和增強過程中，充分考慮人類記憶特征，引入長時記憶和短時記憶更新方式，采用不同的揮發系數，從而使得在路徑更新和選擇過程中呈現更具層次的多樣性。在本文對提出的MIACO進行了理論分析和仿真驗證分析，充分證明了算法所具有的優越性。