基于支路勢能脊方法的風電電力系統暫態穩定評估與控制

王 曼

（南京工程學院，江蘇 南京 211167）

0 引言

由于采用了不同于傳統同步發電技術的風電機組，大規模風電并網給電力系統穩定運行帶來了新的挑戰。風電電力系統的暫態穩定評估更是當前風電并網研究中的重點。

目前，電力系統暫態穩定評估方法主要有時域仿真法、能量函數法和人工智能方法[1]。時域仿真法通過求解全系統的微分代數方程組，利用擾動后狀態變量的變化規律對系統運行的穩定狀態進行評估。此方法能夠計及元件詳細模型，計算結果精確可靠；但耗費機時、計算量大始終是限制該方法廣泛應用的瓶頸；另外也很難給出系統穩定裕度的定量指標[2]，一般用作離線分析和其他分析方法的校驗手段。人工智能方法基于經驗信息，通過建立輸入和輸出間的非線性映射關系，為系統運行狀態的判別和控制做出決策[3]。自動學習的高效算法和大量精確反映系統特征的學習樣本的獲取[4]是目前關于人工智能方法研究的關鍵。能量函數方法基于Lyapunov穩定定律，通過構造包含系統運行和干擾等大量信息的能量函數，直接判斷系統暫態穩定性。Padiyar[5]建立了結構保持模型下包含阻尼、自動勵磁調節系統的詳細發電機能量函數，研究了這種詳細模型能量函數在判別多機系統暫態穩定的有效性。蔡國偉[6]提出了支路勢能函數的概念，認為系統勢能由分布在系統中所有支路勢能之和構成。Ando[7]提出了勢能脊的概念，認為系統故障后越過勢能脊說明系統失去穩定性；但目前尚未有將勢能脊方法應用于風電電力系統的研究，能量函數方法在風電電力系統暫態穩定中的研究也不夠豐富。

本文將支路勢能概念與勢能脊方法相結合，提出了支路勢能脊研究方法和基于支路勢能脊的支路暫態穩定指標。利用支路勢能脊僅僅通過支路勢能及其導數進行計算，無須計及復雜發電機機組模型的特點，將其應用于風電電力系統，使用支路暫態穩定指標判斷系統受干擾后的穩定薄弱環節，并通過在薄弱支路投切晶閘管控制串聯補償裝置TCSC（thyristor controlled series compensator）提高系統的暫態穩定性。

1 支路勢能脊法理論

1.1 支路勢能函數

依據支路勢能理論[8-9]，對于一個有n個節點、m臺同步發電機、l條支路的多機系統，系統的暫態勢能VPE可以描述為

式中：δk和表示故障后某時刻和故障后系統穩定平衡點處第k條支路兩端相角差；Pk和為該時刻和故障后穩定平衡點第k條支路的有功潮流。

第k條支路沿故障后軌跡的勢能VPE,k（δk）可表示為

式中：tc為故障切除時刻；Vi、Vj為支路k兩端i、j點的電壓幅值；xk為支路k的電抗。

由于同調區內節點相角具有相同的變化規律，可認為同調區內勢能為0，系統勢能可以簡化為系統中所有臨界割集支路勢能之和。

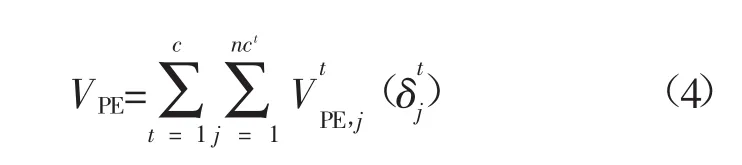
式中：c為系統臨界割集數量；nct為第t個割集中的支路數；VPE，j為表示屬于割集t的第j條支路勢能。

又因同一割集內所有支路兩端電壓Vi、Vj和相角差σk分別具有相同變化規律，所以某割集支路勢能可以表示為割集中任意支路勢能的倍數，故系統簡化勢能式（4）還可寫為

1.2 支路勢能脊法

勢能脊方法繼承發展了暫態穩定勢能邊界曲面 PEBS（potential energy boundary surface） 方法,該方法假設系統持續故障軌跡穿越勢能邊界曲面，勢能在此刻取得最大值；但Ando通過分析仿真發現，實際系統在很多情況下持續故障的勢能軌跡并不一定穿越勢能邊界曲面，導致PEBS方法有較大的分析誤差。“勢能脊”（potential energy ridge）方法的提出，提高了算法的可靠性。所謂“脊”可以理解為勢能在支路相角差空間的所有最大值點所構成的集合。體現了在δ空間中等勢能面作用在δk方向上的作用力。勢能VPE,k在到達脊時在δk方向最大，表明在系統軌跡越過勢能脊后，被拉向背離穩定平衡點的方向，故系統失去同步。

由支路勢能表達式（2）和系統簡化勢能的表示式（5），系統的支路勢能脊即為

1.3 基于支路勢能脊的支路暫態穩定指標和系統

薄弱環節的判別

式中：ta為首次取得極小值的時刻，指標越大，說明該條支路越不穩定。

由此，可依據各支路穩定指標判斷系統薄弱環節：故障后計算各支路暫態穩定指標，Mik最大的支路即為系統薄弱環節，由其構成的割集即為系統暫態失穩的臨界割集。在系統薄弱環節安裝合適的補償裝置就有可能提高系統的暫態穩定性。

2 采用支路勢能脊法的風電系統暫態穩定判別與控制

支路勢能脊方法以系統割集支路勢能及其導數的變化率作為系統暫態穩定和支路穩定程度的判別依據，不涉及發電機組具體數學模型，具有普遍的適應性，同樣適用于包含風電場的電力系統。

作為目前風電市場上的主流機型，異步運行的雙饋異步風電機組不存在功角失步問題；但高滲透率的風電功率的接入，對系統中同步機組的功角穩定帶來深刻影響。

本文以支路勢能法研究風電電力系統暫態穩定性，通過計算系統受擾后各支路勢能及其一階、二階導數，判斷系統是否越過勢能脊，對系統是否保持暫態穩定做出評估，并依據各支路的暫態穩定指標，在失穩前識別系統穩定的薄弱環節，通過在穩定薄弱支路投切TCSC，以提高系統暫態穩定性。

可控串補TCSC通過快速、連續調節串入電網的電抗，可以減小機組間的電氣距離，提高電網的輸送能力，增加機組的同步力矩，從而提高系統的暫態穩定性。

以單機無窮大系統（如圖1所示）為例，由于裝設TCSC后發電機和大系統之間的等值電抗有所減小，若發電機空載電動勢Eq和無窮大母線電壓U保持恒定，補償前后的功角特性曲線分別如圖2中實線和虛線所示。可見，同樣原動機輸入機械功率P0情況下，裝設了TCSC的系統大大提高了系統的能量極限，能夠增加系統故障后的減速面積，提高系統的暫態穩定性。

圖1 單機無窮大系統裝設TCSC

圖2 單機無窮大系統裝設TCSC的功角特性

多機系統中，大干擾后系統穩定薄弱環節支路承擔的暫態勢能出現了急劇變化，抑制薄弱環節支路的暫態勢能變化能夠有效避免暫態失穩，防止系統的同步在此處被“撕裂”。本文正是依據風電系統中各支路暫態穩定指標大小識別系統穩定的最薄弱支路并作為TCSC的安裝點，投切補償裝置，以達到提高系統穩定性的目的。

3 含風電WSCC9節點系統暫態穩定分析

為了驗證支路穩定指標判別系統穩定薄弱支路的有效性和TCSC對提高多機系統暫態穩定的效用，本文以修改的WSCC 3機9節點系統進行仿真分析。系統如圖3所示，同步發電機采用經典二階模型；負荷為恒功率模型；使用額定裝機容量為100 MVA的雙饋異步風電機組替換原系統中母線3處的同步發電機組，雙饋風電機組采用四階模型，模型和參數參見文獻 [11]。風速為雙參weilbull模型，參數：K=2，C=20。系統仿真步長為0.05 s。假設母線7處在t=1 s時發生三相短路故障，t=1.25 s時清除故障，故障清除后系統結構與原系統相同，則式（7）中即為系統故障前穩定狀態時支路k流經的功率。由支路勢能脊方法，連接母線7、8的支路2在t=1.35 s時刻越過勢能脊，系統失去暫態穩定。同步發電機1、2功角時域仿真曲線如圖4所示，支路穩定指標如表1所示。

表1 含風電WSCC9系統三相短路故障時的系統支路暫態穩定指標

根據支路穩定指標，連接母線7、8的支路2和連接母線7、5的支路4為系統穩定的薄弱支路。在系統的這兩條支路上裝設TCSC，如圖2中所示，可控串補的最大補償度分別為50%和60%。安裝TCSC之后，同樣在母線7處三相短路，故障持續0.25 s后清除故障，系統不再越過勢能脊，系統恢復為穩定狀態。此時系統中另外2臺同步發電機轉子角速度之差的變化規律如圖5所示。投切了可控串補之后，同樣故障下，風電系統由暫態不穩定恢復到了暫態穩定，證明了支路暫態勢能指標在判別系統薄弱支路的有效性以及TCSC對提高風電系統暫態穩定性的作用。

圖3 WSCC9 BUS系統圖

圖4 未裝設TCSC系統故障時發電機功角搖擺曲線

圖5 投切TCSC的發電機1、2功角差值曲線

4 結論

支路勢能法與暫態勢能脊概念結合，給出了基于支路勢能脊的支路暫態穩定指標；將其應用于含風電的多機系統，驗證了這種支路暫態穩定指標在風電電力系統識別穩定薄弱支路的適用性。后續工作可以進一步研究故障軌跡預測及支路暫態穩定指標對穩定薄弱支路的超前識別問題。