基于分治法求解對稱三對角矩陣特征問題的混合并行實現(xiàn)①

朱京喬,趙永華

1(中國科學院 計算機網(wǎng)絡信息中心,北京 100190)

2(中國科學院大學,北京 100049)

對稱矩陣的特征求解問題在科學計算領域普遍存在,包括計算物理、計算化學、結(jié)構(gòu)力學、納米材料等前沿學科.通常的處理方法是先通過正交變換把原矩陣化為三對角矩陣,如使用Householder 或Givens方法,再求解三對角陣的特征值和特征向量,然后映射回原矩陣的特征值和特征向量.三對角陣的特征求解算法有很多種,常見的有QR 法、二分法、MRRR 方法和分而治之方法等等.由于QR 法和二分法求解特征向量時往往需要顯式的正交過程,時間復雜度為O(n3),常用于中小規(guī)模矩陣的特征求解.而分治法和MRRR 法能避免這一過程,分治法的平均時間復雜度僅為O(n2.3),其分而治之思想對于大規(guī)模矩陣特征問題的并行求解求解有著天然的優(yōu)勢.

分而治之求解對稱三對角矩陣特征問題的算法最早由Cuppen 提出[1],后M.Gu和S.C.Eisenstat 等人作出改進,提高了該算法求解的特征向量的正交性[2],使得該算法能夠在實際求解中應用.該算法采用分而治之思想,將原矩陣劃分為若干子矩陣,先求出子矩陣的特征分解,再通過修正計算,逐級合并子矩陣的結(jié)果,回代得到原矩陣的特征分解.分治法具有很強的靈活性,適合大規(guī)模三對角矩陣特征問題求解的并行化求解.

分治算法的并行化工作很早就開始展開[3-5],如基于分布式存儲的MPI 進程級并行,基于共享內(nèi)存的openMP 線程級并行,還有基于SMP 的MPI/openMP混合并行等模型.并行化的實現(xiàn)主要基于數(shù)據(jù)并行的考量,通過劃分數(shù)據(jù)到多個核或節(jié)點上計算,在負載均衡的條件下能取得較好的并行效果.但對于分治和遞歸類的場景,當數(shù)據(jù)依賴呈現(xiàn)復雜的網(wǎng)狀結(jié)構(gòu)時,難以實現(xiàn)理想的負載均衡效果.

基于任務的并行編程模型按照功能將一個應用劃分成多個能并行執(zhí)行的模塊,可以是細粒度的,也可以是粗粒度的.常見的任務并行模型有TBB,Cilk和SMPSS 等,使用這些模型時無需關心任務的具體分配和調(diào)度細節(jié).

Cilk 作為一個基于任務的并行編程模型,為共享內(nèi)存系統(tǒng)提供了一個高效的任務竊取調(diào)度器,適合用來為分治和遞歸類算法實現(xiàn)高效的多核任務并行.對于并行編程,Cilk 為串行程序的并行化提供了向量化、鎖、視圖等機制[6],通過關鍵字來聲明操作,改造后的代碼具有語義化、可讀性強的特點.

1 分治算法求解的基本原理

1.1 矩陣劃分

對任意n階實對稱三對角矩陣T,基于秩1 修正從第k行作如下劃分：

其中,T′1,T′2是三對角子矩陣塊,ek代表第k個元素為1 的單位向量,元素β是T的第k個副對角元素.為使修正矩陣元素一致,對T1的末位元素和T2的首元素都減去了相同的元素.

分治過程一般采用折半劃分,對于劃分后的矩陣T′,若規(guī)模未達到指定閾值,則繼續(xù)劃分.

1.2 分治法求解過程

若劃分后的子矩陣規(guī)模達到設定閾值,調(diào)用QR或者其他算法得到子矩陣T’1,T’2的特征值分解：

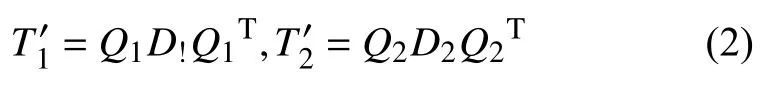
令修正向量

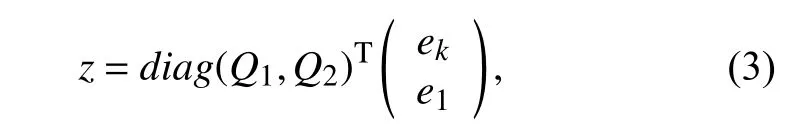
則矩陣T的特征分解如下：

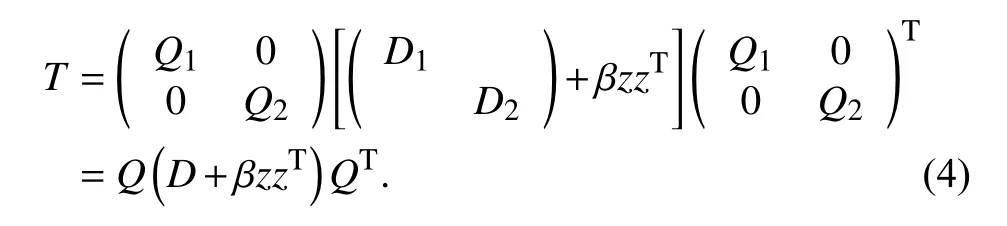
令D+βzzT=W,因為diag(Q1,Q2)為正交矩陣,所以T和W相似有相同的特征值,求T的特征分解T=QΛQT,可以通過先求出W的特征分解：W=PΛPT,再令Q=diag(Q1,Q2)P,即可求得T的特征分解.

對于W的特征分解,需要根據(jù)劃分后矩陣的特征值和原矩陣特征值之間的間隔性[7],通過求解對應的secular 方程(3)：

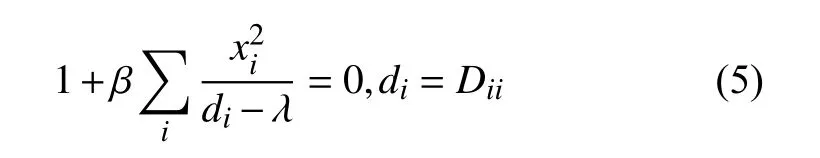
得到相應的的特征值λ.文獻[6]討論了方程(3)根的分布特性和解法,在特征區(qū)間內(nèi)使用牛頓法或拉格朗日法迭代逼近區(qū)間內(nèi)的特征值,線性時間內(nèi)即可收斂.解出所有的特征值后,再通過式(D-λI)-1x[1]求得每個特征值對應的特征向量,回代到式(1)中得到T的特征分解.

整個求解過程在邏輯上可看作樹型結(jié)構(gòu),在葉子結(jié)點上進行特征求解,在非葉子結(jié)點上進行特征合并.

1.3 注意事項

文獻[5]中指出合并過程中如果D的主對角線上出現(xiàn)了相同的元素或者z向量中出現(xiàn)0 元素時,在迭代前進行deflation 操作可以避免特征區(qū)間內(nèi)迭代不收斂的情況.通過Givens 正交旋轉(zhuǎn)變換,部分特征值和特征向量就能原地得到.如果求得的特征值前后過于接近,按原方法求得的特征向量會丟失正交性,文獻[8,9]討論了特征值間隔過小時的特征向量的求法,避免了顯式正交過程.文獻[2]根據(jù)特征問題的反問題給出了特征向量的改進求法,保證了計算結(jié)果的正交性.

2 分治算法的并行化

2.1 節(jié)點內(nèi)并行實現(xiàn)

單節(jié)點內(nèi)求解三對角矩陣塊的特征分解主要包含兩個過程,分別是求出最小劃分矩陣的特征分解以及逐步合并特征值和特征向量.由于每個子矩陣的特征計算以及同級子矩陣之間的合并過程是相互獨立的,下面結(jié)合Cilk 模型給出遞歸實現(xiàn)的分治算法在單節(jié)點多核環(huán)境下的并行化算法.

算法1.分治算法基于Cilk 的節(jié)點內(nèi)并行1) 判斷輸入矩陣的規(guī)模,如果矩陣規(guī)模小于等于設定 閾值,執(zhí)行2)；否則執(zhí)行3)；2) 調(diào)用特征求解算法進行特征分解,返回結(jié)果；3) 劃分矩陣T 得子矩陣T1,T2,通過Cilk 執(zhí)行任務劃分,并行地對T1,T2 遞歸調(diào)用步驟1),求出子矩陣的特征值和特征向量后,進行排序和迭代逼近等操作合并子矩陣的特征值和特征向量,得到T 的特征分解,返回結(jié)果.

Cilk 在程序遞歸執(zhí)行過程中不斷劃分新的任務,產(chǎn)生Cilk 線程去處理,并把其分配到空閑的核上,和父線程并行執(zhí)行.一個Cilk 任務是在同步、生成新線程或返回結(jié)果之前執(zhí)行的最長序列化指令集或代碼段[10].求解過程中,遞歸調(diào)用T1之前的過程可看作任務A,遞歸調(diào)用T2的過程可看作任務B,同步及合并過程可看作任務C.現(xiàn)假設程序只進行了四次嵌套調(diào)用,則全局任務劃分后生成的任務流如圖1所示.

2.2 多節(jié)點混合并行實現(xiàn)

實現(xiàn)分治算法的多節(jié)點并行,需要先把原始矩陣按邏輯樹結(jié)構(gòu)劃分成小的子矩陣分發(fā)到葉子結(jié)點上進行初步計算,然后通過MPI 通信匯總每棵子樹的計算結(jié)果,把整理后的結(jié)果重新發(fā)送到子結(jié)點進行合并操作,重復此過程,直到返回到樹的根結(jié)點.為了減少進程間通信,充分利用Cilk 任務并行機制,需要對原矩陣進行較粗粒度的劃分,以榨取單節(jié)點處理器的計算性能.

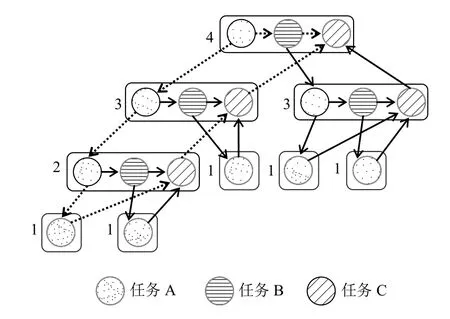
圖1 分治算法的任務并行流程

對于n階對稱三對角矩陣T在N個進程上的特征求解,假設N=2k,n=2j,算法初始時把原矩陣劃分為N個子矩陣,每個子矩陣階數(shù)為2j-k,下面給出分治算法在多節(jié)點上的混合并行實現(xiàn).

算法2.分治算法基于MPI/Cilk 的節(jié)點間并行首先,對于劃分到N 個進程上的每個初始子矩陣,調(diào)用算法1 求出各部分特征值和特征向量；接著,進行p 輪循環(huán)(p 對應邏輯樹的高度).每輪循環(huán)先把進程分組并確定主控進程.每個MPI 進程根據(jù)自己的進程類別按序選擇執(zhí)行下列步驟：1) 組內(nèi)進程通過互補通信交換求得的局部特征向量矩陣,接著向主控進程發(fā)送本進程求得的局部特征值和拼接的修正向量；2) 主控進程收集所有組內(nèi)進程求得的局部特征值進行排序,并保留排序后的位置索引數(shù)組,并根據(jù)此數(shù)組將修正向量排序,將排好序的特征值和修正向量劃分到組內(nèi)各進程；3) 組內(nèi)進程接收主控進程發(fā)送過來的排好序的部分特征值和修正向量,求解secular 方程和特征向量；4) 各組內(nèi)進程按列執(zhí)行分塊矩陣乘法,更新當前輪循環(huán)的部分特征向量矩陣,接著執(zhí)行下一輪循環(huán).

2.3 算法分析

圖1最上方左面對應遞歸的最外層,每個出度大于1 的結(jié)點都會派生出新的Cilk 線程,執(zhí)行新的任務.程序執(zhí)行過程產(chǎn)生的所有的Cilk 線程數(shù)為圖1中節(jié)點數(shù),關鍵路徑長度為圖1中虛線部分路徑長度.程序的并行性為Cilk 線程數(shù)與關鍵路徑長度之比,執(zhí)行時間大于等于所有任務平均到每個核上運行的時間和關鍵路徑上任務運行花費的總時間.

算法2 中在對特征值進行排序后,同時記錄排序后各位置元素的原來位置的索引,避免對特征向量重復排序,方便下一輪特征向量的計算.在第p輪循環(huán)中,從0 號進程開始每2p+1個進程分為一組,每隔2p+1個進程被選為選為主控線程.更新局部特征向量矩陣時,為了減少數(shù)據(jù)通信開銷,避免主控進程進行統(tǒng)一收發(fā),使組內(nèi)進程間只進行必要的局部特征向量的互補交換,然后按列執(zhí)行分塊矩陣乘法,分別計算更新的特征向量矩陣的部分,通信量為O(n2/N).

算法1和算法2 中的合并過程涉及大量計算密集型操作,占據(jù)程序執(zhí)行的主要時間,可以使用Cilk 提供的數(shù)據(jù)并行機制加速.Cilk 通過數(shù)據(jù)劃分形成一個個可供調(diào)度的線程級任務并行執(zhí)行,通過基于貪心策略的任務竊取方式執(zhí)行調(diào)度：當一個核完成自己的任務而其它核還有很多任務未完成,此時會將忙的核上的任務重新分配給空閑的核.

由于在迭代計算不同特征值的近似值時,所執(zhí)行的迭代次數(shù)可能不同,均勻分配任務可能導致線程間的負載不平衡.Cilk 通過工作密取機制從其他線程獲取一部分工作量,能夠避免單核上出現(xiàn)任務過載和饑餓等待的問題,同時能將密取的次數(shù)控制在最低水平,減少密取帶來的性能開銷.若單節(jié)點內(nèi)劃分的數(shù)據(jù)粒度適當,就能利用Cilk 機制充分發(fā)揮多核處理器的計算和調(diào)度能力,得到較好的負載均衡.

3 實驗結(jié)果與分析

我們在中科院“元”超算上的cpuII 計算隊列進行了數(shù)值實驗,節(jié)點上搭載的是Intel E5-2680 V3 芯片,每塊芯片包含12 顆主頻為2.5 GHz 的計算核心.MPI程序使用Intel mpiicpc 編譯并鏈接到Cilk Plus 運行時.實驗對象是30 000 階主對角元素是4,副對角元素是1 實對稱三對角矩陣.矩陣劃分求解的規(guī)模閾值設為200 階,實驗最終求出全部特征值和特征向量(通過環(huán)境變量設置每個節(jié)點使用2～12 個Cilk 線程進行實驗).

表1是MPI 模型與MPI/Cilk 混合模型在4～128個核、2～12 個Cilk 線程參與計算下所用時間匯總.從表中可以看出,相同計算條件下MPI/Cilk 混合并行計算時間要少于純MPI 方法,而隨著參與計算的Cilk 線程數(shù)的增加,計算用時也越來越少,這表明當計算任務密集時,計算效率隨著可供調(diào)度的線程的增加而增加.當參與計算的Cilk 線程數(shù)超過10 時,對于當前規(guī)模的矩陣計算獲得的加速提升效果逐漸變得有限,這是因為Cilk 是基于貪心策略執(zhí)行調(diào)度的,當任務粒度較小時不會頻繁的執(zhí)行任務竊取,從而減小系統(tǒng)開銷.而在較少節(jié)點參與計算時,獲得的加速效果較為明顯,這說明對數(shù)據(jù)進行粗粒度劃分時能取得較好性能.

圖2是MPI 模型和MPI/Cilk 模型在不同參數(shù)下的加速比變化趨勢曲線(已測出在單節(jié)點單線程環(huán)境下的平均串行時間為880 秒左右).可以看出,隨著參與計算的核數(shù)和Cilk 線程數(shù)增加,三條曲線的上升趨勢都逐漸變得平緩,出現(xiàn)這種現(xiàn)象的原因主要為計算任務粒度變細和進程間通信開銷增加導致的.MPI/Cilk方法的曲線在一開始上升較快,隨著進程數(shù)的增加,計算任務粒度逐漸減小,加速效果也隨之下降,但仍比純MPI 方法變緩得更慢.這表明MPI/Cilk 方法的并行效果要優(yōu)于純MPI 方法,擁有更好的可擴展性.隨著可供調(diào)度的核數(shù)增多,使用更多的Cilk 線程數(shù)參與計算能獲得更好的計算性能,Cilk 動態(tài)調(diào)度的優(yōu)勢也漸漸體現(xiàn)了出來.

表2給出了MPI/Cilk 模型(使用8 個Cilk 線程)同ELPA、ScaLAPACK 軟件包實現(xiàn)的分治算法求解30000 階矩陣特征的計算時間比較.ELPA和ScaLAPACK 是求解線性代數(shù)問題領域中應用廣泛的并行軟件包.從表中數(shù)據(jù)可以得出,當參與計算的核數(shù)較少時,MPI/Cilk 方法與ELPA、Scalapack 中分治算法計算用時接近,隨著參與計算的核數(shù)增多,MPI/Cilk方法、ELPA 方法與ScaLAPACK 方法的計算性能逐漸拉開,但本文的MPI/Cilk 方法與ELPA 方法的擴展性仍然存在著一定差距.這是由于ELPA 按照塊級循環(huán)分布矩陣,實現(xiàn)了對計算流程的更細粒度的控制.

表1 MPI 模型和MPI/Cilk 模型運行時間

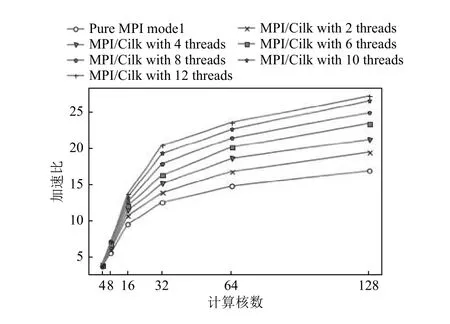
圖2 MPI 模型和MPI/Cilk 模型的加速比曲線

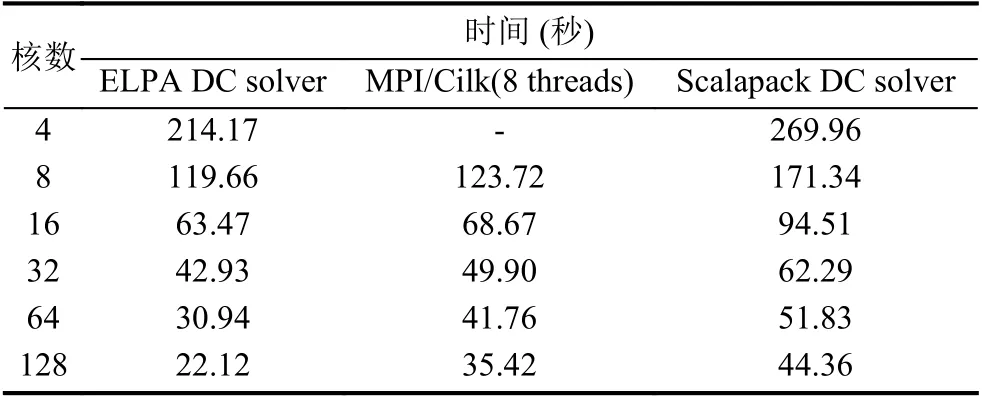
表2 MPI/Cilk 方法與ELPA、ScaLAPACK 求解器時間對比

4 結(jié)論與展望

本文針對對稱三對角矩陣特征求解的分治算法,提出了一種改進的基于MPI/Cilk 的混合并行實現(xiàn).在節(jié)點間,進行粗粒度計算任務的劃分,更新局部特征矩陣時通過弱化主控進程的中心作用,使組內(nèi)進程之間只進行必要的互補數(shù)據(jù)交換,避免了統(tǒng)一收發(fā)流程,減少了進程間的通信開銷；在節(jié)點內(nèi),利用Cilk 的任務并行機制提高了CPU 的利用率和特征求解過程中的負載均衡性.實驗結(jié)果體現(xiàn)了該算法的性能.本文實現(xiàn)的分治算法與最新的ELPA 軟件包仍然存在一定的性能差距,還有可以提升的空間.此外,Cilk 線程啟動數(shù)和數(shù)據(jù)劃分粒度對計算性能的影響以及同openMP 等其它任務并行模型的效果對比等等是值得進行下一步研究的方向.