基于變尺度搜索算法的混沌MIMIC算法

趙晉彬,夏桂梅

(太原科技大學 應用科學學院,山西 太原 030024)

分布估計算法(EDAs)的基本思想是利用變量間的概率分布來表示變量之間的相關關系,并經過迭代進化,迫近問題的最優值,降低了對問題先驗知識的要求,是一個很好的連鎖學習算法[1]。混沌算法是一種收斂較快的優化算法,具有遍歷性和隨機性。這樣的特征,可用于局部優化,但它有初值選擇的敏感性,因此傳統的混沌算法對目標難以瞄準。變尺度搜索可以縮小搜索區間,使得算法更容易找到最優解[2]。在MIMIC算法和混沌搜索算法結合的前提下,引入變尺度搜索,優化搜索空間,提出基于變尺度搜索算法的混沌MIMIC算法(MSCS-MIMIC)。

1 MSCS-MIMIC

1.1 MIMIC算法

MIMIC算法是一個在雙變量相關、鏈式結構依賴假設基礎上提出的分布估計算法,其概率圖模型如圖1所示[3]。

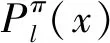
圖1 MIMIC的概率圖模型Fig.1 Probabilistic graphical model of MIMIC

1.2 混沌算法(CS)

在混沌優化算法中,通常選擇Logistic映射所產生決策變量,其形式如下[4-5]:

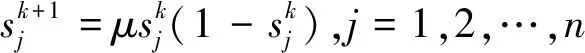
(1)

其中:μ為操控參數,當μ=4時,處于完全混沌的狀態,且xn在(0,1)范圍內是遍歷的。

混沌搜索算法步驟如下:

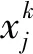
1.3 變尺度搜索(MS)

1.3.1搜索空間映射

由Logistic映射所產生的決策變量xn∈[0,1]必須映射到向量空間,即混沌搜索的上限和下限[a,b]。本文采用的映射公式如下[6]:

x′n=ci+dixn

(2)

式中，ci和di為與邊界有關的系數,ci=a，di=b-a.

1.3.2變尺度搜索

以當前最優解x*為中心,通過[7-9]

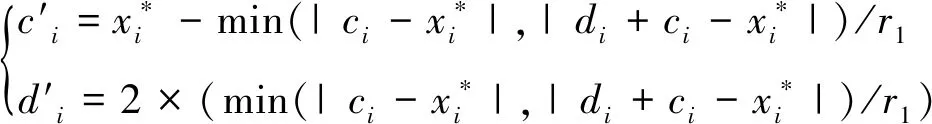
(3)

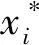
(4)

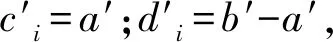
(5)

將式(5)和a=ci，b=ci+di分別代入式(3)即得式(2)。

圖2 變尺度搜索示意圖Fig.2 Schematic diagram of mutative scale optimizing search

1.4 MSCS-MIMIC算法

混沌搜索算法與MIMIC算法結合,旨在解決MIMIC算法局部搜索問題和CS算法對初值的高要求問題[10-11],在算法中引入變尺度搜索,可以重構優化變量取值空間,大大提高了結果的準確性。

算法實現過程如下:

步驟1:隨機生成若干個體組成初始種群N。

步驟2:評估初始群N,如果連續搜索至相同值或找到最終的最優解,算法結束,否則進入下一步驟。

步驟3:使用截斷選擇、輪賭選擇,將S個變量選出作為主導變量群,其中S=N/2。

步驟4:按照貪婪算法構建優勢模型:

a.根據in=argminjhl(Xj)找出排列π=(i1,i2,…,in)中的in；

b.對任意k=n-1,…，1,根據ik=argminjhl(Xj|Xk+1),其中k≠ik+1…,in，計算出排列π=(i1,i2，…,in)；

步驟5:優勢群體用CS算法進行搜索,對搜索后的優化值進行評價,并更新已知的最優值[12]。

步驟6:使用變尺度方法略微減小變量的取值區間,即以當前最優解為中心,通過(3)式所述,調整ci和di來重構優化變量的值空間。

步驟7:合并種群,將根據模型產生的優勢變量與保留的優勢群體組成新的種群,轉到步2。

2 算法性能測試及分析

2.1 參數設置

為檢測新算法的性能,并與CS-MIMIC算法、MIMIC算法比對,對下面6個無約束函數進行檢驗[13]。

在實驗中,MIMIC算法的參數設置如下[14]:群體數量N=300,截斷選擇為N/2,最大迭代次數范圍[10,50],這里選擇30次。進行混沌搜索法的迭代次數為30次,對優勢群體的20%進行迭代實驗。

函數1:

minf(x)=f(1,1,…,1)=0

函數2:

minf(x)=f(0,0,…,0)=-105

函數3:

函數4:

minf(x)=f(0,0,…,0)=0

函數5:

minf(x)=f(0,0,…,0)=0

2.2 實驗結果及分析

本文通過三種情況對實驗數據進行歸納總結,得出MSCS-MIMIC算法的優勢。

1)在種群更新代數、迭代次數以及維數相同的情況下,三種算法是不是能夠收斂到最優解。本文取更新代數為200,迭代次數30次,維數M=2。

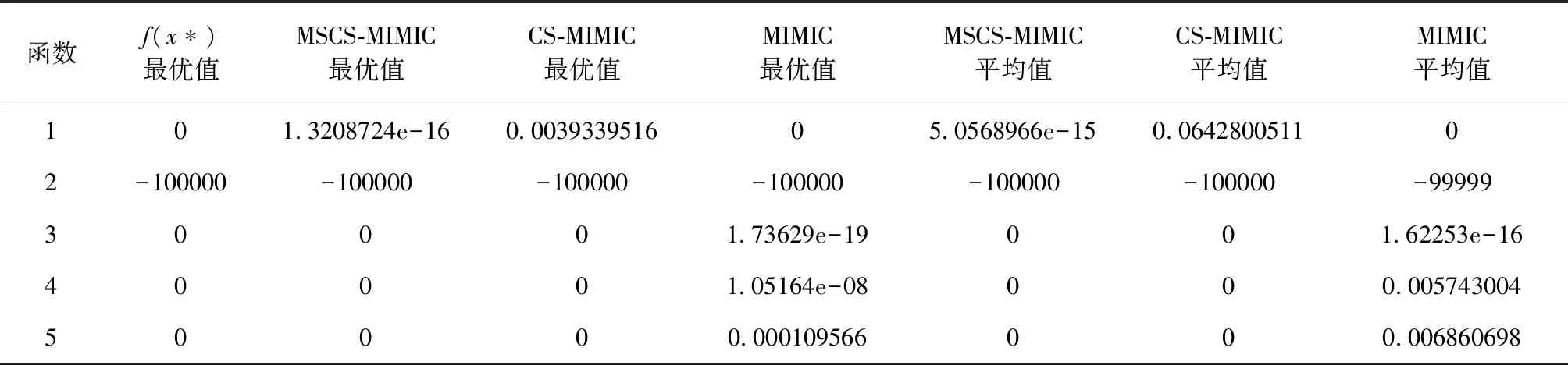
表1 200代內算法優化所得結果Table 1 The results of optimization within 200 generations

表1顯示了三種算法進行30次獨立實驗的結果。可以看出,對于測試函數f1,MIMIC算法收斂到了最優值,而MSCS-MIMIC算法以CS-MIMIC算法更高的精度收斂到最優值附近,說明引入變尺度算法提高了新算法的收斂能力。其余函數,第一、二種算法的搜索結果對應于函數的最佳值,而MIMIC算法只找到了f2的最佳值。

2)在維數不變的情況下,算法運行結束后進化代數的均值。取維數M=2,進化代數為200。

表2 到達確定最優值的平均進化代數

表2是三種算法平均進化代數的比較結果。可以看出,MSCS-MIMIC算法的結果都較小,其中對于函數1,MSCS-MIMIC算法精度更高的前提下,算法的平均進化代數更小,這與算法中引入混沌搜索算法有很大的關系。而且在其余函數的試驗中,MSCS-MIMIC算法都在收斂到最優值的前提下,運行了更少的進化代數。

3 結論

基于變尺度搜索算法的混沌MIMIC算法(MSCS-MIMIC)不僅繼承了CS-MIMIC算法尋優能力高和運行速度快的特點,此外它還提升了算法的細化能力和穩定性,是一種有效的優化算法。從兩組實驗得出的數據可以看出,結合了變尺度搜索算法的混沌MIMIC算法能夠以較高的精度收斂到最優值附近,或者直接收斂到全局最優值,并且最優值可以在較小的進化代數內找到,這對改進類似優化算法提出一種新的嘗試。