小概率原理及其應用

秦秉杰

(山西藥科職業學院 基礎部,山西 太原 030031)

0 引言

生活中我們通常習慣于關注發生可能性較大的事情,其中原因在于概率論源于對賭博問題研究,在這種問題里我們當然關心那些勝率較大的策略。相應地,在考察概率分布時,我們重點關注的也是這個分布的峰值,概率統計諸多理論就是在研究“峰值”,大數定律和中心極限定理都使得人們習慣于相信隨機現象在大尺度下的穩定性,因此人們關注大概率事件是有理論依據的。

但是我們在重視大概率事件的時候,也不能忽視小概率事件。我們工作和生活中就有一些事件,它們發生的可能性很小,但一旦發生危害卻非常大。比如2011年溫州動車相撞事件、2015年長江游輪傾覆事件、2017年九寨溝的地震事件等,這些事件發生概率很小,危害卻很大,因此不能忽視,對這些問題的研究也非常必要。

1 小概率事件的概念及小概率原理

1.1 小概率事件的概念

我們知道,自駕出行有可能出交通事故,坐飛機可能遭遇失聯,可為什么我們沒有裹足不前,還要出游呢?我們知道,抓彩票可能中大獎,可為什么我們沒有一哄而上、趨之若鶩呢?這是因為我們知道,這些事情發生的可能性太小了!

可能性也即概率,那么多小的概率算小呢?這個不能一概而論。比如某工廠生產一批燈管,不合格率是1%都可以出售,而醫藥企業生產的藥品,不合格率是0.1%都不能出售,這是因為醫藥產品事關人類的生命健康,標準自然要高一些。

不過,在數學上,一般將發生概率小于0.05的事件稱為小概率事件。

小概率事件還具有突發性和誘惑性兩個特點,比如地震、海嘯的發生等往往比較突然,而各種賭博游戲往往是利用豐厚的大獎來誘惑人們參與。

1.2 小概率原理

概率很小的事件在一次試驗中幾乎是不會發生的,這就是小概率原理;反之,如果事件發生了,有理由懷疑原假設是錯誤的,這也稱為實際推斷原理。

根據概率論中的伯努利(Jakob Bernoulli)大數定律,在試驗條件不變的情況下,事件A發生的頻率依概率收斂于事件A發生的概率,即在大量重復試驗時,可以用事件A發生的頻率來代替事件A發生的概率。這時如果事件A發生的概率很小,則在大量重復試驗中它出現的頻率也會很小。例如,假設事件A發生的概率P(A)=0.01,那么在100次試驗中,大約只有1次出現A。

表 摸球游戲規則及輸贏概率Table Rules and probability of winning or losing in touch ball game

2 小概率原理在實際生活中的應用

2.1 在規避街頭騙局方面的應用

日常生活中,我們經常遭遇一些街頭騙局,譬如下面的摸獎騙局。莊家在一個袋子里放6個紅球和6個白球,這些球除了顏色不一樣以外,其它完全一樣。游戲規則為,每次任意從袋子中摸6個球,輸贏規則如表所示。

這個規則看上去對顧客有利,因為7種情形只有一種是輸錢的,其它6種情形你不用投資,均能賺錢。很多人禁不住誘惑,難免心動去試一試,但結局往往卻是掃興而歸,輸的錢從幾十到幾百不等。問題出在哪呢?我們不妨計算一下:

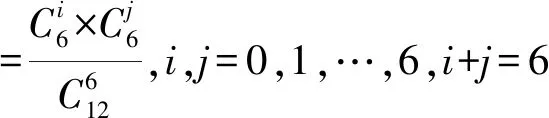
由此可以算得各種情況輸贏的概率如表所示。

可以看到,贏100元和贏50元對應概率都小于0.05,是小概率事件,在一次試驗中幾乎不可能發生,因此可以忽略。觀察的重點是贏20元概率總計是0.487,而輸100元概率是0.433,因此從平均下來輸錢可能性更大。莊家就是利用小概率原理,設計使得贏錢的概率很小,因此賭的越多,輸的就越多。

2.2 在風險投資方面的應用

1994年成立的美國長期資本管理公司(LTCM),曾經是世界上著名的對沖基金。該基金聚集了一大批世界高智商精英,專門從事金融市場套利,是當時與量子基金、歐米伽基金、老虎基金齊名的國際四大“對沖基金”之一。

LTCM的投資模型是“不正常市場價差套利”。他們利用計算機追溯大量的歷史交易數據,通過獨特的算法,得出兩種標之間“正常”的歷史價差,如果現有價格與正常歷史價差出現了“非理性”的偏差,計算機便隨之建立標的組合,大舉入市套利。

LTCM所遵循的就是“市場中性”原則,無多無空,主要以尋求標的效率落差形成的套利空間,并通過對沖化解市場風險。公司成立后的幾年,這套交易模型取得了輝煌的交易成績:3 a間其資產凈值從12.5億美元上升到48億美元,增長了2.84倍。

然而1998年這個巨人卻轟然倒塌,公司一夜之間倒閉了,這是為什么呢?

其中一個主要因素是這一年出現了罕見的小概率事件!

1998年,由于國際油價下跌,導致國內經濟下滑、政局不穩,俄羅斯政府不得不采取“非常”的舉動,宣布盧布貶值,國債交易也隨之停止。這一舉動,導致國債市場出現空前極端的波動,疊加LTCM投資杠桿很高,短期內就產生了巨額損失,無力支撐,最終被監管機構接收。

LTCM案例給我們的啟示是,歷史數據和規律并不能等同未來,歷史不會簡單重復,市場環境的變化可能導致出現小概率事件,而這可能導致以前規律的失效。因此在投資中,對小概率事件的忽視可能導致極其嚴重的后果[1]。

2.3 在保單設計方面的應用

概率論是研究隨機現象統計規律性的一門學科,而保險就是利用隨機現象的統計規律性來化解風險的,保險與概率論密切相關,概率論是保險的數理基礎。下面我們以一個保單設計案例看看概率論在其中的應用。

案例1:根據調查數據,某年齡段人的死亡概率為0.001。現有某保險公司要據此設計一份人壽保單,具體條款是:投保人每年繳納300元保費,如果投保人當年死亡,保險公司負責賠付受益人10萬元。現有1萬人投保,問保單的設計合理嗎?

分析:假設投保者1 a內死亡人數為x人,則x～B(10000,0.001),公司一年的收入為1萬×200=200萬,賠付金額為10萬×x=10x萬元。若保險公司虧損，需200<10x,即x>20,即賠付人數大于20人。

投保人數n=10000數值很大,而死亡概率p=0.001數值很小,因此該分布可以用泊松分布近似,其中泊松分布的參數λ=np=10。

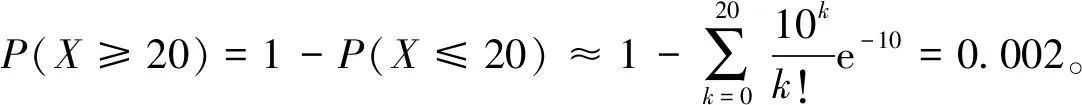
2.4 在質量管理方面的應用

小概率原理在藥物研發、疫苗接種、藥品生產等方面都有廣泛的應用。

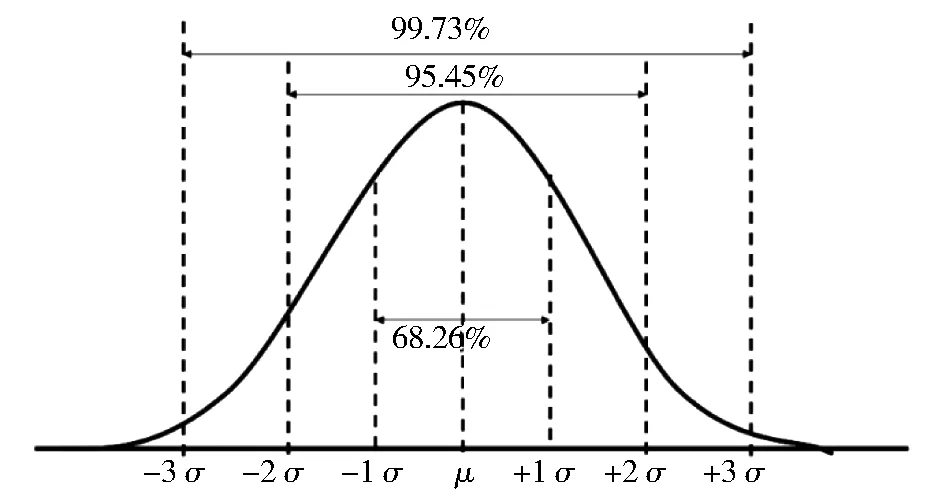
圖1 正態分布的3σ準則Fig.1 Normal distribution 3σ criteria

案例2:某個藥品生產企業生產一種片劑,其質量服從正態分布,設質量為xmg,x～N(1000,202)。抽檢時發現有某一片劑質量為1 080 mg,問該藥品能否通過質量檢查?

解析:根據正態分布的3σ準則(圖1),該片劑質量落在(μ-3σ,μ+3σ)區域的概率幾乎為1,也就是落在(940,1060)內的概率幾乎為1。但是現在抽檢結果為1 080 mg,并沒有落在這個區域,這就說明發生了小概率事件。而小概率事件在一次試驗中幾乎是不可能發生的,現在發生了,就懷疑該批產品可能有問題,因此藥品不能通過質量檢測[3]。

3 如何正確理解小概率事件

對于小概率事件,人們通常會有兩種極端反應。

一種極端反應是麻痹大意,把小概率事件等同于不可能事件。要注意,小概率事件并不是不可能事件。不可能事件是發生概率為0,是必然不會發生的事件,而小概率事件概率雖然小,在一次試驗中發生的可能性也很小,但大量重復試驗后,其發生的可能性卻幾乎是必然的。

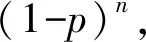
生活中,我們也有很多諺語講的是這樣的道理,比如“瓦罐不離井邊破,只怕來的遭數多”“常在河邊走,哪能不濕鞋”等[5]。

另一種極端反應是過分放大。比如2011年的動車相撞事件,民間反應很大,甚至導致官方被動降低高鐵速度;還比如有些人經常看車禍視頻,心理產生陰影,對高速路出行產生了恐懼心理等。其實這些情況本質上是一種小樣本認知偏差,即在夸大了小樣本條件下事件的概率對總體概率的代表性,這也是不對的。

總之,小概率事件反映了生活中一類特殊而重要的現象。全面正確認識這類事件,既可以避免無謂的損失,又可以在矛盾時找到有利的取舍依據。我們應該認識和把握好這個工具,讓它更有效地為我們服務。