小口徑高炮對高速目標毀殲概率研究

鄧輝詠，何循來，殷軍輝，王 聰，張偉召

(1.陸軍工程大學石家莊校區，河北 石家莊 050003；2.南通理工學院，江蘇 南通 226002；3.陸軍炮兵防空兵學院，河南 鄭州 450007)

小口徑高炮由于射速高、初速快，射擊密集度高，在近程具有較高的效費比，是己方高價值目標的末端防空武器。有效的高炮對目標毀殲概率的計算模型，能夠對高炮武器系統的效能分析、方案評價和作戰研究提供有力保障。

對高炮毀殲概率的研究，許多學者做了積極探索，肖元星[1]等較系統地研究了高炮武器系統著發、近炸、空炸射擊時的毀殲概率模型，但在計算著發時，采用解析法，模型推導過程作了較大簡化，不能計算下滑、俯沖等任意航路的點射毀殲概率。文獻[2]基于蒙特卡羅法，采用仿真的思路計算著發射擊毀殲概率，能夠對任意目標、任意飛行航路的毀殲概率進行計算，但這種方法需要對目標的外形輪廓進行簡化，目標輪廓方程不易建立。文獻[3-4]對彈丸初速、彈道系數以及目標飛行參數對著發射擊毀殲概率的影響進行了研究；文獻[5]根據射擊誤差的相關性和重復性，研究了各類誤差的產生方法，其本質還是簡析模型的運用。

現代高炮武器系統，尤其是自行高炮在伴隨防空過程中，兩炮間隔有時可達1 000 m以上，因此必須考慮配置地域帶來的炮目距離差引起的毀殲概率變化，另外，對于高速運動目標，例如彈道末速度達550 m/s的鉆地精確制導炸彈，必須考慮點射時各發彈彈著點引起的毀殲概率變化。筆者在分析射擊誤差來源的基礎上，結合仿真法和解析法，逐彈逐炮計算對目標的毀殲概率，進而求取一次點射毀殲概率。

1 射擊誤差分析

在理想情況下，不考慮誤差，彈丸能夠在提前點準確命中目標，但由于誤差的存在，實際彈著點與理想彈著點有偏差。高炮的射擊誤差包括[6]：不相關誤差、弱相關誤差、強相關誤差和系統誤差(由于現代高炮基線已經修正，不考慮單炮系統誤差)。

1)不相關誤差。不相關誤差指以同樣的射擊諸元發射多發彈，由于各種隨機因素影響而造成的實際彈道與理論彈道的偏差，表現為彈丸在彈道平面內隨機分布，其均值為0，通常用高低和方向散布中間誤差或均方差來描述，一般用σN、σZ表征。在用仿真法計算高炮毀殲概率時，散布誤差為不相關誤差，服從正態分布，可用直接抽樣的方法生成服從某個方差分布的隨機數。

2)弱相關誤差。弱相關誤差包括：火控解算系統和跟蹤系統引起的誤差σr1、σr2，火炮隨動系統和穩定系統引起的誤差σr3、σr4.跟蹤時每發彈的提前點均存在誤差，因此σr1、σr2與點射長度相關；而σr1還應增加火控系統之間的誤差，因此與點射長度和火控系統有關；σr3、σr4與點射長度和火炮有關，牽引高炮無穩定系統，σr4取0.弱相關誤差可認為相關系數為(0，1).

3)強相關誤差。強相關誤差包括氣象測量誤差σq1和初速準備誤差σq2.σq1與某次點射所處的條件有關，主要包括修正空氣密度誤差均方差σΔk、修正縱風風速誤差均方差σFx、修正橫風風速誤差均方差σFz；顯然，σq2也只與射擊條件有關，一般用修正初速準備誤差均方差σv0p表征。強相關誤差可以認為相關系數為1的誤差。

4)高低角和方位角的系統誤差σφ、σβq.該誤差只與火炮有關，在彈道平面內表現為與理想點實際偏差。

前述的相關性是指同一時刻每發彈是一致的，但在不同時刻，后一發彈對前一發彈具有相關性。對于弱相關誤差，認為是方差數和相關系數已知的正態分布數，可以先隨機生成所需要服從分布的隨機數，再經過相關的抽樣模型處理。

2 仿真模型

2.1 相關性誤差抽樣模型

由于高低和方位誤差的相關性很小，因此可以將二維問題轉換成兩個一維平穩隨機問題。首先根據點射長度n，生成n個獨立的服從的隨機數{u1,u2,…,un}，則考慮相關性誤差時第k發彈的隨機誤差抽樣ηk為[7]

(1)

式中：α為相關系數；Δt為兩發彈時間間隔，取Δt=60/(ph),h為單管分鐘射速,p為管數。

2.2 誤差合并

從前面分析可知，火炮隨動系統和穩定系統產生相關性誤差時機是一致的，為了提高計算機的運行速度，可以將這兩個誤差合并。設隨動系統和穩定系統的相關系數分別為r3、r4，則合并后的相關系數rh和方差σh為

(2)

(3)

顯然，對于牽引高炮σr4取0后，合并表達式退化成只含隨動系統誤差。

2.3 考慮地域配置不同的處理

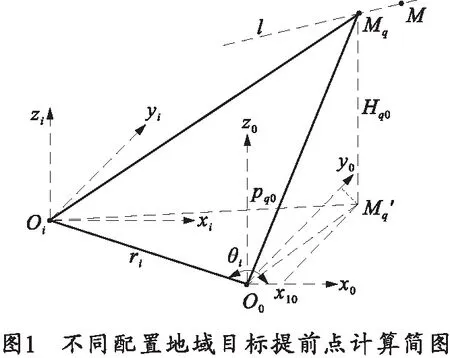
考慮到高炮的配置范圍不會太大，因此忽略配置地域在高度上的差異。設基準炮位于O0點，建立基準坐標系O0-x0y0z0，目標提前點Mq在基準坐標系中的坐標為(x10,pq0,Hq).第i門炮位于Oi點，其在基準坐標系中的坐標為(ricosθi，risinθi，0)，在Oi點建立第i門炮的坐標系Oi-xiyizi，各坐標軸與基準坐標系各軸同向，各炮與基準炮相對位置關系如圖1所示。則目標提前點在坐標系Oi-xiyizi中的坐標為

(4)

2.4 毀殲概率表達式

強相關誤差和弱相關誤差在仿真計算時，首先按散布誤差生成正態分布的隨機數，然后按2.1節方法對各數據進行相關性處理，計算毀殲概率時可依次抽取處理后的誤差數據，作為某發彈的諸元誤差，結合散布誤差和系統誤差，則可按文獻[1]中單管單發的模型計算第i發彈的毀殲概率，即

(5)

式中：A=(a1,a2)T為高低和方位系統誤差組成的列向量；Σ為高低方位散布誤差組成的矩陣、相關性處理后高低方位射擊諸元誤差(除系統誤差)組成矩陣和，其中氣象測量誤差和初速準備誤差矩陣中各元素的求取參考文獻[1]，其余誤差對角元素分別為高低誤差和方位誤差，其余元素為0；w為毀殲目標所需平均彈數；l為目標三向面積在彈道平面內投影面積等效正方形邊長，該參數與彈丸終點速度、目標速度和目標飛行姿態相關[1]，而目標在任一時刻的速度和飛行姿態可通過目標的航路數據/方程得到。

由于仿真需要大量的計算，直接用積分求單發毀殲不經濟，有必要對其進行變換，通過變換，式(5)可變換為

(6)

(7)

式中：λ1、λ2為Σ的特征值；θ為Σ對角化的單位正交陣角元素，其計算式為

(8)

式中，σij為Σ中的元素。

由于式(6)為標準正態分布概率密度函數積分，可轉化為

(9)

φ(x)的近似計算式可見文獻[1].經過轉換近似計算，Pki由積分式轉換成乘法運算，使計算效率大大提高。若有m門火炮，每門火炮有p個身管，每管發射n發彈，則進行一次點射的毀殲概率為

(10)

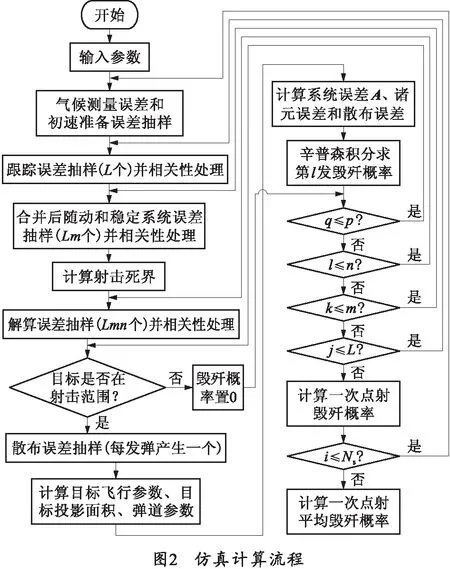
2.5 仿真流程

圖2為小口徑高炮對高速目標毀殲概率的仿真計算流程，圖中Ns、L、m、n、p分別為仿真次數、火控門數、火炮門數、單管射彈發數以及火炮身管數。為了提高計算精度，應盡可能提高仿真次數Ns.

3 仿真算例

為了驗證計算方法的正確性，用解析法和本文方法分別進行計算，計算條件：某35高炮的誤差和射表數據，2門高炮射擊，極坐標參數設為(0，0)，單管18發；目標數據：三向面積分別為0.833、0.833、0.221 m2，俯沖角0°，速度340 m/s，航捷500 m，高度200 m，目標臨近，平均毀殲彈數為1.34.

為了有比較性，用本文的方法計算時，強制點射過程中目標位置不改變，仿真次數設300，計算數據如表1所示。

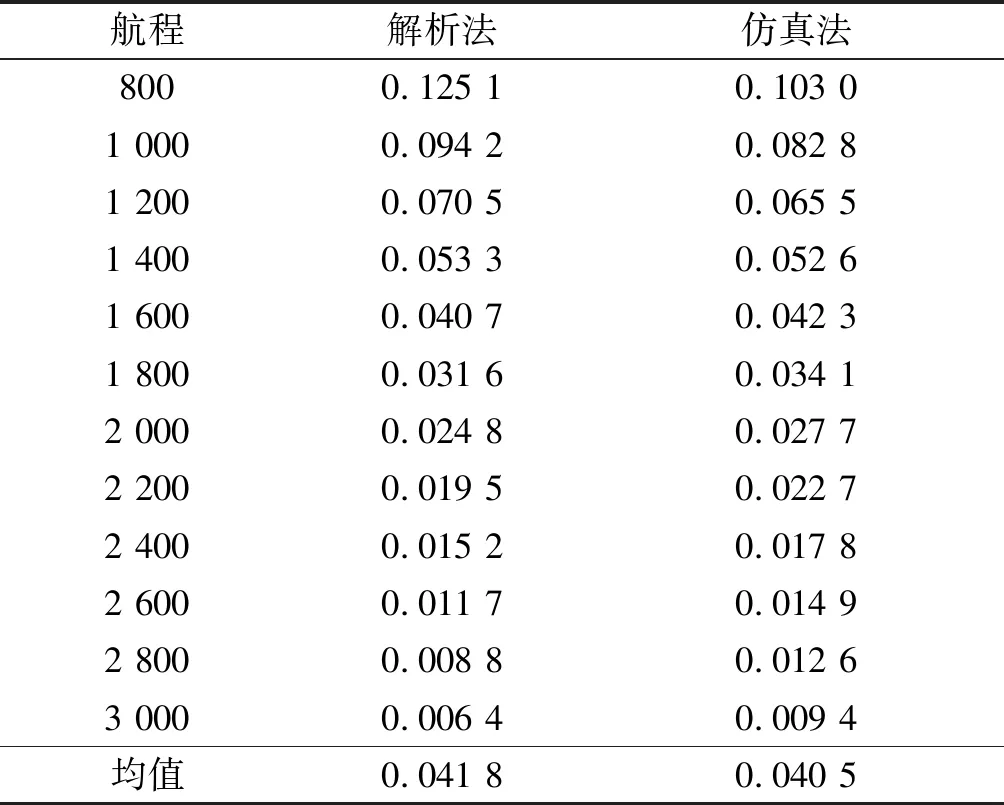
表1 某35高炮不同航程對目標的毀殲概率 m

從仿真的結果來看，整個航程的平均毀殲概率吻合較好，相對誤差約為3.1%，說明本文計算方法的正確性，但本文的計算結果更符合指數函數的變化規律，即在航程的兩端變化較平緩，而中間變化較快，與適用的指數毀殲率相符。

以文獻[1]中例6.1基本數據為例，第2門炮相對于基準炮的極坐標為(500 m,120°).目標按表2中數據飛行(時間為基本變量，中間值按4次樣條插值獲取)。在時間t=0,1,2,…,5 s時刻分別做一次單管18發的點射。

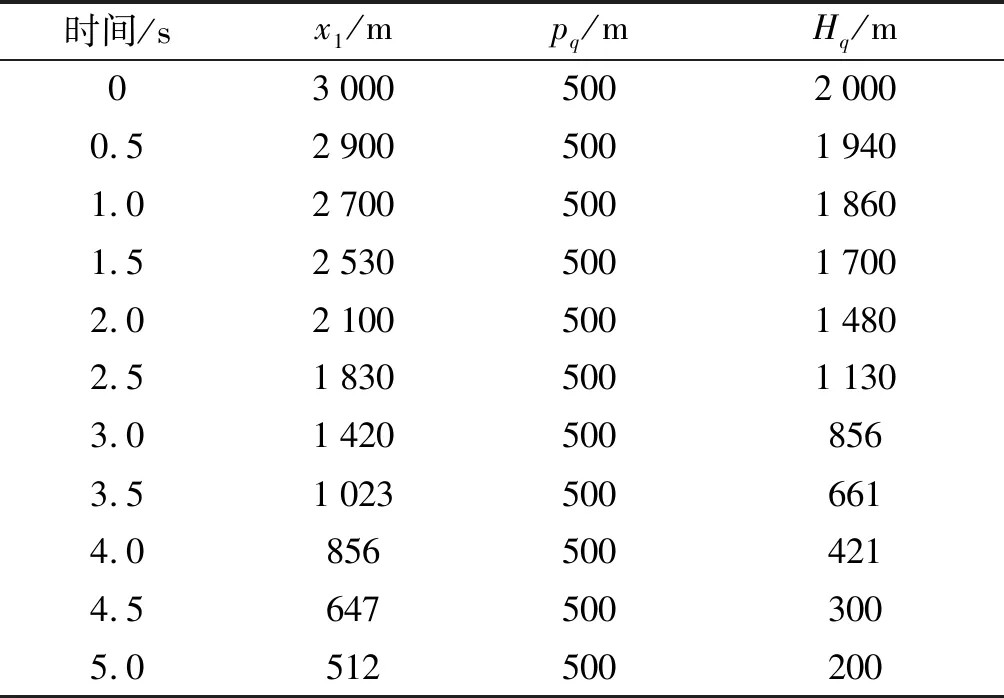
表2 目標飛行航路數據

通過MATLAB編制程序仿真計算，得到各時刻點射的毀殲概率數據，如圖3所示。

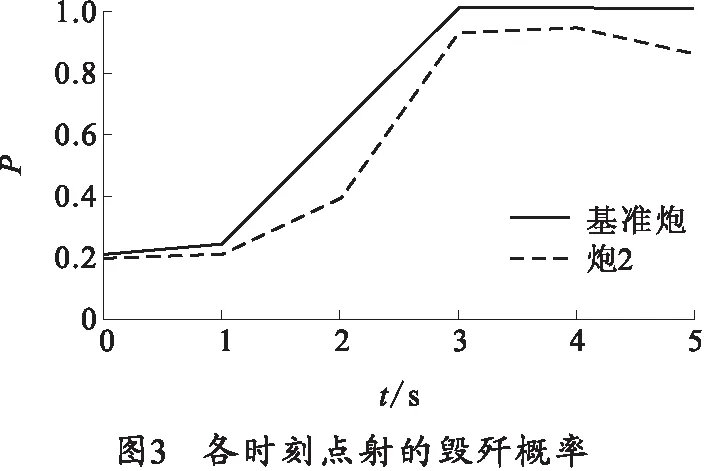
從圖3可以看出，炮2的毀殲概率總體上比基準炮要小且其變化趨勢基本一致。這是由于目標相對于炮2比相對于基準炮的航路截徑和航程都較大。因此，在計算多炮協同作戰的毀殲概率時，必須考慮各炮的配置地域。

圖4為t=3 s時刻點射各發射彈的毀殲概率。

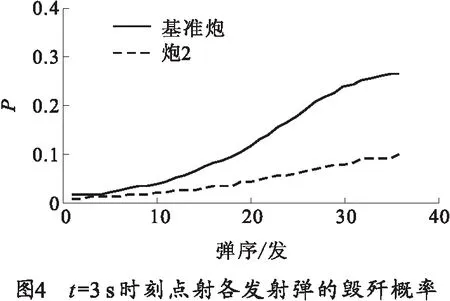
從圖4可以看出，各發射彈的毀殲概率總體上具有不斷增加的趨勢。這是因為在t=3 s時刻，目標的絕對速度達到980 m/s，而兩發彈的時間間隔為0.056 s，即在該時間間隔內，目標向陣地臨近約50 m.隨著目標的不斷臨近，各發彈的毀殲概率不斷增加，因此在計算高速運動目標時，必須考慮目標位置的變化。

4 結束語

筆者通過對射擊誤差分析和其中相關性誤差抽樣建模，設計了用解析法計算高炮單管單發毀殲概率進而求取一次點射毀殲概率的計算方法;并給出了仿真計算流程。該方法只需輸入目標的三向面積，不需對目標的外形輪廓建模，簡化了計算。另外，該方法考慮了火炮配置地域差距、點射時間差帶來的毀殲概率影響，適合對高速目標毀殲概率的計算。