面向風電數據的WSN壓縮感知數據重構

吳 潮 邵 帥

(1.蘭州交通大學 機電技術研究所，甘肅 蘭州 730070; 2.甘肅省物流及運輸裝備信息化工程技術研究中心，甘肅 蘭州 730070； 3.甘肅省物流與信息技術研究院，甘肅 蘭州 730070； 4.蘭州交通大學 機電工程學院，甘肅 蘭州 730070)

無線傳感器網絡(Wireless Sensor Network，WSN) 是將大數量的傳感器節點布置在目標區域中，這些節點通過自組織(感知、采集、處理和傳輸)的方式構成數據傳輸的網絡，最終到達用戶手中。目前風電場普遍采用測風塔來對風電數據進行采集，數據量大、錯誤數據、冗余數據多，通過GPRS傳輸會出現丟包嚴重的現象，而使用無線傳感器節點來對風電場進行布局，構成網絡，能夠使采集的數據更加全面與準確，從而全面準確地反映整個預測區域的真實氣象情況[1-5]。但是風電場的地域面積寬闊，在用無線傳感網絡對風電場進行布局，為了得到全面、精準的采集數據，需要提高無線傳感器網絡的覆蓋性和可靠性，采用高密度的節點部署方式，會產生覆蓋區域的重疊、數據冗余的現象，這樣不加篩選的大數據傳播會快速耗盡傳感器節點的能量。因而，應融合傳感器節點采集的數據，減少網絡中的數據傳輸量，提高數據的傳輸效率。壓縮感知算法作為近年來研究較為廣泛的一種數據融合算法，能夠從較少的采樣數據中精準重構出原始數據，有效減少數據的采樣和傳輸。

壓縮感知理論是由華裔科學家陶哲軒等人近年提出來的[6]。將壓縮感知理論與常用的奈奎斯特采樣理論進行比較發現，壓縮感知理論在對數據進行采集的過程中，同時對數據進行處理篩選，這就保證了傳輸過程中數據的完整性與真實性[7]。稀疏基、觀測矩陣和重構算法是壓縮感知理論的3個組成部分，重構算法對于整個壓縮與重構過程起著決定性的作用。目前比較成用的重構算法可以分為三大類：凸優化算法[11-12]、組合算法[13]和貪婪算法[8]，其中凸優化算法與其他兩種算法比較具有運行速度快、運算量小的優點，更加適合應用在WSN中。

分段弱正交平匹配追蹤(SWOMP)算法是目前應用較為廣泛的貪婪算法之一。這一算法的運算速度快，且算法簡單，但是該算法在運行的時候需要對門限參數進行設定，門限參數的選取對于重構精度的影響較大[8]；再者是該算法在從冗余字典中選取最佳因子時，采用的是內積法則度量準則，這種方法在殘差信號匹配的過程中會導致部分原始信號的丟失[9]。本文就門限參數與度量準則對于SWOMP算法重構精度的影響進行研究分析，首先采用自適應的方法把最優的門限參數選取出來，再通過Dice系數替換掉內積法則，選取出最佳因子，提高重構的成功的成功率。

1 壓縮感知理論與SWOMP算法原理

1.1 壓縮感知理論

與傳統的奈奎斯特采樣理論比較，壓縮感知理論在采集數據完整重構中使用的數據數量更少。下面為壓縮感知理論的采樣公式[10]，其中信號x為稀疏表示：

y=Φx

(1)

式中，Φ為M×N的觀測矩陣。但是實際中的信號大多是不稀疏的，這就需要通過稀疏基Ψ進行稀疏化處理，信號x表示為

x=Ψθ

(2)

式中,Ψ為N×N的稀疏基;θ為K稀疏的矩陣，為信號x通過某變換域進行稀疏的表示 ，令

A=ΦΨ

(3)

將采樣信號表示為

y=Aθ

(4)

使用選擇的Ψ與Φ矩陣對傳輸回來的信號y進行重構，得出信號x。

目前在無線傳感器網絡中常用的稀疏基有離散傅里葉變換、小波變換、離散小波變換等，測量矩陣目前常采用稀疏隨機測量矩陣、隨機高斯矩陣、隨機伯努利測量矩陣等。

1.2 SWOMP算法原理

分段弱正交匹配追蹤(SWOMP)算法是正交匹配追蹤(OMP)算法的一種改進的算法，對原有的原子選擇方法進行了改進，通過門限參數的設定，采用內積法準則度量方法來選擇最優因子在冗余字典中。

傳統的SWOMP的算法流程如圖1所示。

從圖1中能夠發現，門限參數在迭代中對原子的選擇起決定性作用，這樣無法得到最優原子，過大或者過小的門限參數均會使原子的選擇結果偏差極大;當觀測矩陣中存在兩個相似的原子時，如果選用內積法來選擇最佳原子，這就會出現部分原始信號丟失的問題。這兩者均會直接影響重構的效果。

2 SWOMP算法中門限參數對于重構精度的影響

采用的實驗數據是酒泉某風電場2017年1月份的溫度數據。實驗時從風電場的實測數據中選取長度為256的信號作為實驗數據。選取0.2、0.4、0.6、0.8 4個不同的門限參數進行重構實驗，研究并分析門限參數對于重構效果的影響。其中，實驗中采用的稀疏基為快速傅里葉變換，觀測矩陣選用的是高斯隨機矩陣。4個不同門限參數下，SWOMP算法的數據重構效果如圖2所示。

通過分析SWOMP算法不同門限參數的數據重構效果可以發現，不同的門限參數的數據重構效果差異較大，并且重構的成功或失敗與門限參數選取關系較大。

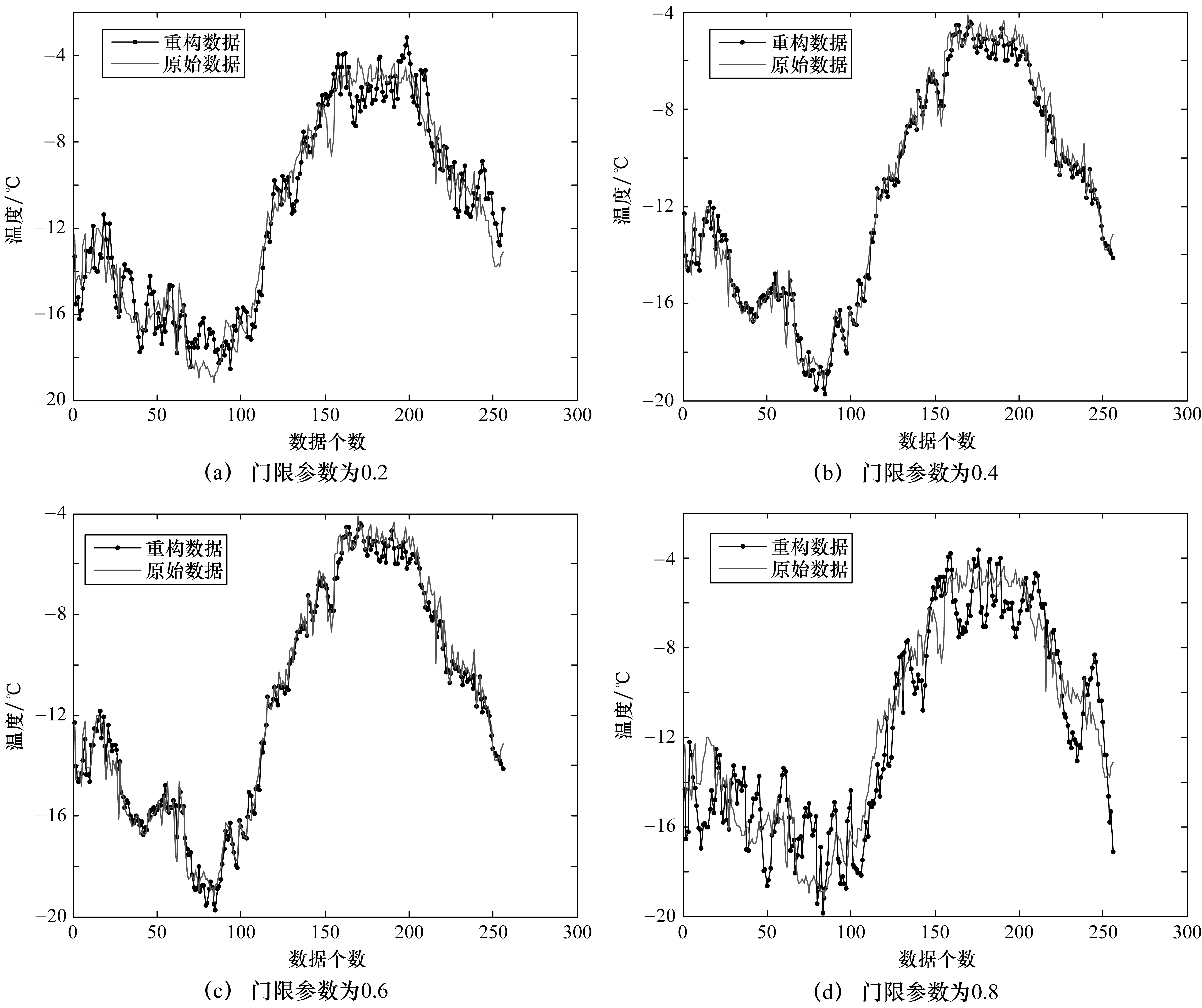
圖2 SWOMP算法不同門限參數的數據重構效果

3 改進的SWOMP算法

3.1 門限參數的自適應調整方法

通過對上面重構實驗的結果分析，發現不恰當的門限參數會導致重構的失敗。并且門限參數選取過程中，不同的采樣信號也將會產生極大的影響。針對重構中存在的問題，自適應的調整方法對于SWOMP算法的門限參數選取具有重要的意義。但是，在最佳門限參數的選取過程中，如果通過帶入的方式來不斷運行重構算法，就會極大降低重構的效率，因此在最優門限參數的選取過程中，自調節的方式將會使運算的次數盡可能少。由于PID方法運算復雜度低、方法簡單，并且當被控對象的數據動態性大、具有非線性時，控制效果較好。在風電場這種條件復雜的無線傳感器網絡應用環境中適合應用。

在SWOMP算法中應用PID方法如下：① 采用觀測矩陣處理采集的數據，得出觀測向量y；② 采用傳統的SWOMP算法對觀測得到的矩陣進行重構，獲取重構信號;③ 得出計算之后的誤差值，比較計算的誤差值與設定的誤差標準；④ 對門限參數用PID方法進行調整。循環執行上述的步驟，直到計算的誤差在設定的誤差標準之下，得出最優的門限參數[14]。

其中，誤差值計算的公式為

(5)

式中，y為觀測向量；x_r為重構信號；Φ為觀測矩陣。當計算出來的誤差值大于設定的誤差標準時，使用PID方法對門限參數進行調整。門限參數的調整公式為

Ts(k)=ts(k-1)+(kp+ki+kd)*error+
(-kp-2kd)*error_1+kd*error_2

(6)

式中，kp為比例系數；ki為積分系數；kd為微分系數。

門限參數的調節值采用上述的式(6)進行計算，下一次計算使用的門限參數即為上一次的門限參數與計算得到的調節值進行相加，通過多次的循環，使得到的誤差值在設定的誤差值之下，便得到需要的最優門限參數。

下面為PID自適應調整算法的流程。

輸入：設定初始門限參數alpha，誤差標準e_base,觀測值y，測量矩陣A。

輸出：重構信號x_r。

① 設定error_1=0， error_2=0。

② theta = CS_SWOMP( y,A,10,alpha)。

③ x_r = Psi * theta。

④ error=norm(y-Phi*x_r)/norm(y)。

⑤ while error>e_base。

⑥ if 相鄰3次調整得出的誤差相似，循環結束 end。

⑦ 通過式(6)得出重構誤差估計值。

比如一天中午，我本來興高采烈的，可媽媽說：“方舟，今天我發了八十八塊錢，和你考的一樣。”說完，又裝作天真無邪的樣子捂住嘴，好像說漏了嘴一樣。我警惕地看了爸爸一眼，爸爸正在做飯，不知他聽見沒有。

⑧ 計算調整后的門限參數。

⑨ error_2=error_1；error_1=error;alpha=a。

⑩ 利用調整后的門限參數再次進行信號重構。

3.2 采用Dice系數匹配準則選取最佳原子

傳統的SWOMP算法在最佳原子的選取中是在冗余字典中使用內積法，將選擇的最佳原子構件為索引集矩陣再與殘差值進行匹配。內積法的選擇方式，由于其分母是對向量分量的平方和求幾何平均值，無法使原子的原始狀態得到保證，不能區分相似的原子，當通過觀測矩陣來匹配殘差信號時，當觀測矩陣中存在兩個相似的原子時，如果選用內積法來選擇最佳原子，這就會出現部分原始信號丟失的問題，影響重構的效果。

在原子選擇的過程中，采用Dice系數匹配準則，其分母是對向量分量的平方和求算數平均值，可以使得每個原子信號的原始狀態得到完整的保存，保證原子的特征不改變。因而最佳原子的選取使用Dice系數，能夠使向量中的每個元素的相關性在求解過程中得到最大限度的應用，從而使得原始信號丟失的問題得以解決。

內積匹配準則計算公式為

(7)

Dice系數匹配準則計算公式為

(8)

Dice系數匹配準則算法如下。

輸入：門限參數alpha，觀測值y，測量矩陣A，迭代次數S。

輸出：重構信號x_r。

① 初始化r0=y,Λ0=φ,A0=φ,t=1。

②u=abs[Dice(ATrt-1)]選取其中大于門限參數alpha的值，將選取值對應的傳感矩陣A的序列號j集合起來為集合J0。

③ 令Λt=Λt-1∪J0,At=At-1∪aj,如果Λr=Λt-1迭代結束。

④ 求y=Atθt的最小二乘解，即

⑤ 更新殘差:

⑥ 計算重構信號x_r。其中，alpha為自適應算法所得到最優門限參數。

4 實驗結果與分析

采用Matlab 7.0軟件在Windows 7系統上對上述算法進行仿真。通過仿真實驗得出最優的門限參數，然后再次仿真得出初始門限參數SWOMP算法，最優門限參數SWOMP算法與Dice系數改進的SWOMP算法的對比圖，通過對稀疏度一定時，信號在不同觀測值M下的重構成功概率進行對比，來對改進算法的性能進行評估。

成功概率公式為

(9)

式中，K為重構成功率；P為重構成功的次數；T為測試的總次數。

驗證試驗通過仿真數據來進行。選用長度256、稀疏度20的數據來進行實驗。初始的門限參數選用0.2，設定的誤差標準為2×10-15。通過對自適應調整方法的程序進行運行，當門限參數為0.46時，誤差在設定的誤差標準之下。

實驗對數據長度為256、稀疏度K=20時，采用初始門限參數SWOMP算法、最優門限參數SWOMP算法與通過Dice系數改進的SWOMP算法對不同觀測值M下進行仿真，得到重構成功率趨勢圖，如圖3所示。

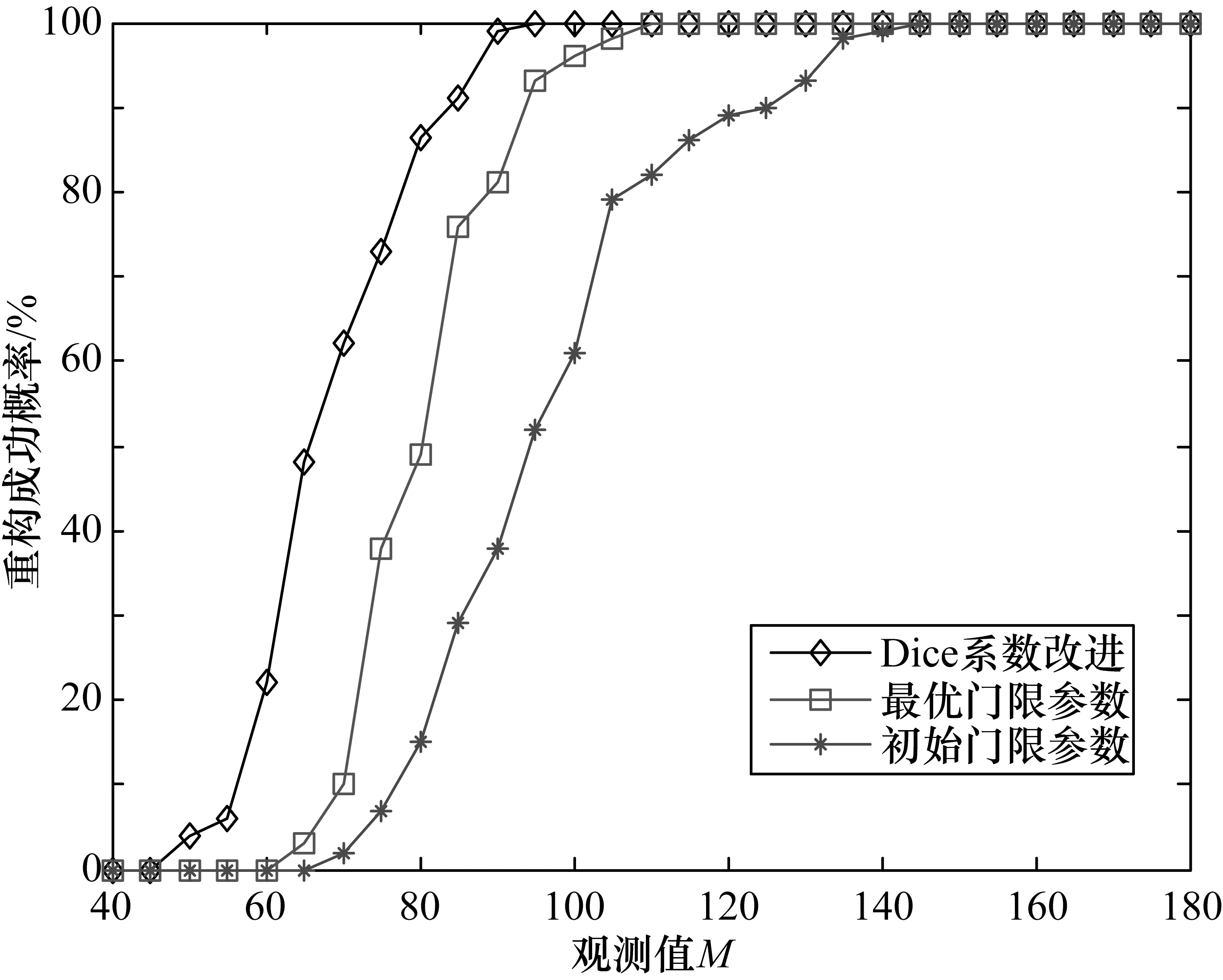
圖3 原始SWOMP與改進的SWOMP算法的重構成功率

通過對仿真結果進行分析，隨著觀測值M的增大，3種設定情況的重構成功率趨勢都是逐步增大的。當觀測值M相同時，最優門限參數比初始門限參數的重構效果好，通過Dice系數改進后的SWOMP算法的重構效果得到進一步的提升。對100%重構時的觀測值M進行觀察，Dice系數改進后的觀測值M最低。

5 結束語

本文就應用于WSN的SWOMP重構算法進行研究分析，通過分析SWOMP算法最佳原子選擇方式以及最優門限參數的選取，對不同門限參數的重構效果進行仿真，得到的重構效果差值較大，并且原子的選擇過程中，原始算法選用內積法，不僅無法得到最佳原子，還可能丟失部分的原始信號。針對原始算法中存在的問題，采用自適應的調整方法來選擇最優的門限參數，通過Dice系數匹配準則來解決原始信號丟失的問題。通過實驗仿真，改進后的算法能夠得到最佳的門限參數，重構效果得到提升。在得出最優門限參數的基礎上，使用Dice系數對原始的內積法進行替換，仿真結果發現，重構效果能夠得到進一步的提升。