有效提升小學生數學解決問題能力的教學對策初探

洪振華

《義務教育數學課程標準（2011年版）》中提出“初步學會從數學的角度發現和提出問題，綜合運用數學知識解決簡單的實際問題，增強應用意識，提高實踐能力。獲得分析和解決問題的一些基本方法，體驗解題方法的多樣性，發展創新意識”。可見，在解決問題的教學中，教師要讓學生經歷數學思考的過程，積累發現問題、提出問題、解決問題的經驗，培養學生問題解決的能力，促進學生形成應用意識、推理能力、創新意識以及良好的思維習慣和能力是十分必要的。

多年小學高年級數學教學實踐，筆者發現不少學生在數學學習中，相比較于計算、概念、幾何圖形等學習內容，感覺最困難的是解決問題，會出現諸如此類的現狀：看到題目不知從何下手;只會依葫蘆畫瓢，仿照例題解題;解決了問題得出了結果，卻說不清算理……

一、問題的緣起

（一）設計問卷，了解學情

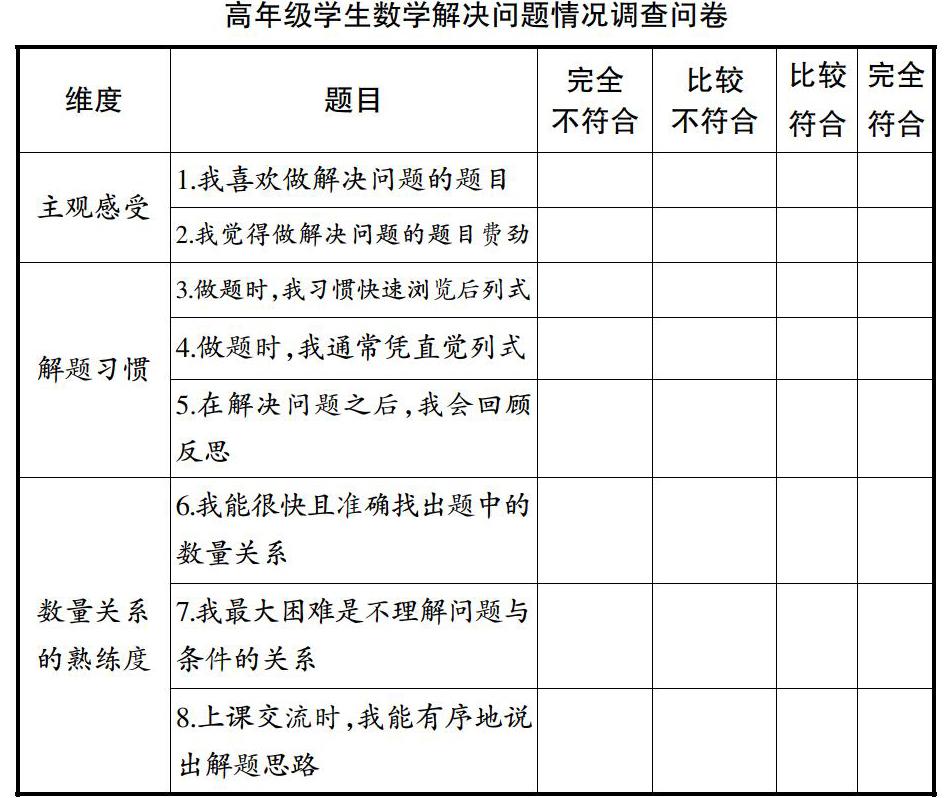
為了尋找高年級學生解決問題感覺困難的原因，筆者設計了一份問卷，從“主觀感受”“解題習慣”“數量關系的熟練度”三個維度共8個子項了解學情。見下表：

（二）分析問卷，尋找成因

1.數據呈現的客觀現狀

發出、收回調查問卷75份，對收集的信息整理后，發現如下情況：

（1）學生不大喜歡做解決問題的題目，覺得相對比較費勁。從“主觀感受”的選項看，第1題“我喜歡做解決問題的題目”選“完全不符合或比較不符合”占60%。第2題“我覺得做解決問題的題目費勁”選“比較符合”占33.3%，“完全符合”占8%。

（2）學生缺乏認真審題和反思檢查的良好習慣。從“解題習慣”的選項看，第3題“做題時，我習慣快速瀏覽后列式”選“完全符合或比較符合”占53.3%;第4題“做題時，我通常憑直覺列式”選“完全符合或比較符合”占48%。第5題“在解決問題之后，我會回顧反思”選“完全符合或比較符合”占28%。

（3）學生分析數量關系的能力較差。從“數量關系的熟練度”的選項看，第6題“我能很快且準確找出題中的數量關系”只有34.7%的選“完全符合或比較符合”;第7題“我最大困難是不理解問題與條件的關系”選“完全符合或比較符合”占45.3%。第8題“上課交流時，我能有序地說出解題思路”選“完全符合或比較符合”只有25.3%。

2.反思主要原因

一是忽視以題論理。知識有形，而題型無限。而課堂教學常常出現“以題論題”，沒有做到“以題論理”，引導學生“理出思路、方法”。一旦面對不同的題型時，學生就會出現“憑感覺，猜算法”的現象。

二是忽視分析數量關系。中低年級解決問題的數量關系相對簡單，學生看題目憑經驗比較容易就能列出算式。教師會有所大意，以為學生懂了，教學的重點發生偏移，數量關系分析不到位甚至缺位。

三是對良好學習習慣的重要性認識不足。學生對解題三部曲“閱讀理解、分析解答、回顧反思”的好習慣未有足夠的重視，對老師的要求只是應付了事，認真審題、回顧與反思的意識普遍淡薄。

二、提升的對策

（一）建立模式，熟悉常見的基本數量關系

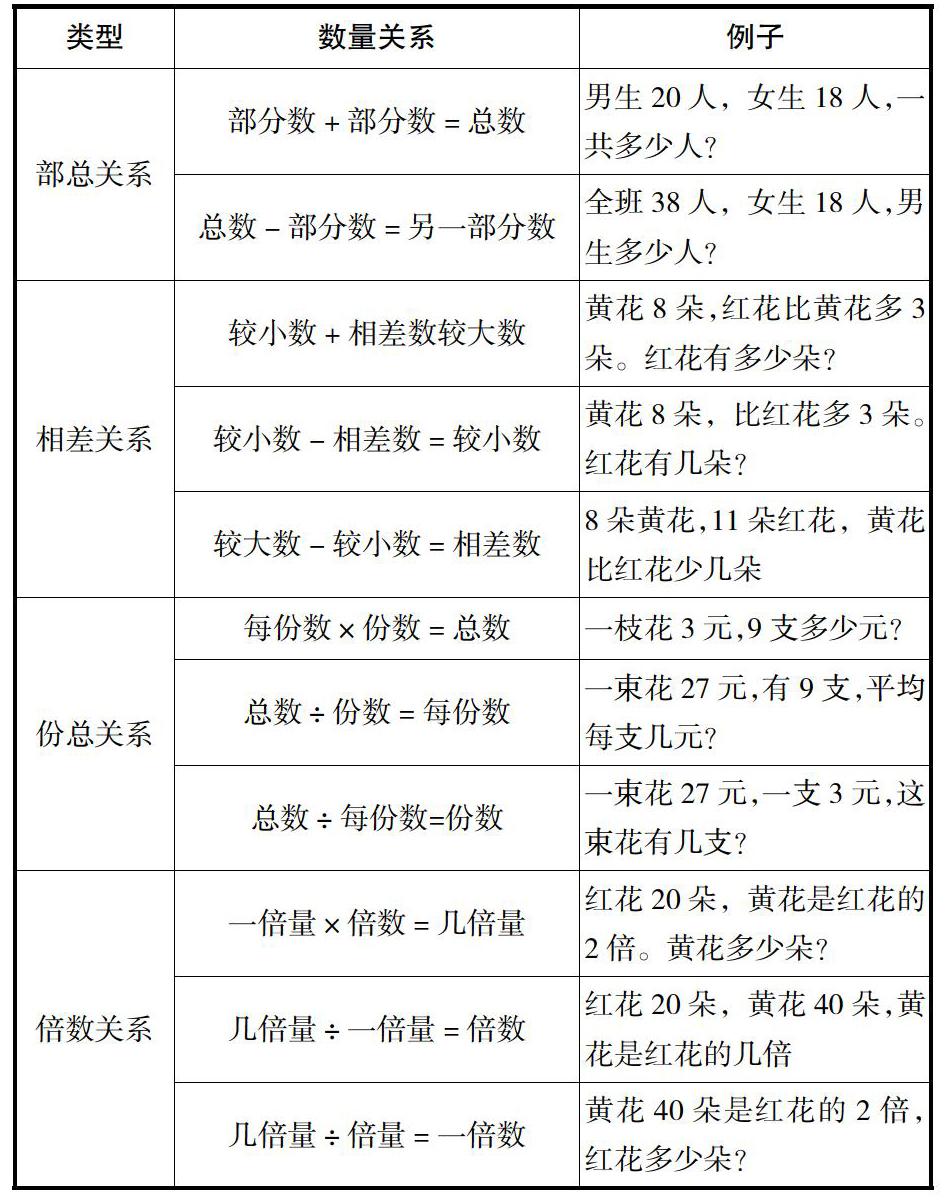
每道簡單解決問題里都存在一定聯系的三個數量，讓學生熟悉數量之間的基本關系，學會分析數量間的聯系，是正確解決實際問題的先決條件。在小學數學解決問題中的基本數量關系一共有四大類，見下表。

（二）啟發聯想，將數量關系融會貫通

1.根據條件聯想問題。如：小紅買了6支筆，小明買了2支。可以聯想：①一共買了多少支筆？用“小紅買的支數+小明買的支數=一共買的支數”;②小紅比小明多買了多少支？或小明比小紅少買了多少支？用“小紅買的支數-小明買的支數=小紅比小明多買的支數”;③小紅買的支數是小明的幾倍？用“小紅買的支數÷小明買的支數=倍數”;④小明買的支數是小紅的幾分之幾？用“小明買的支數÷小紅買的支數=幾分之幾”。

2.根據問題聯想出與相關聯的兩個條件。如“兩天一共運化肥多少噸？”與它相關聯的兩個條件，可以是“平均每天運的噸數”和“運了2天”，用乘法：平均每天運的噸數×運的天數=一共運的噸數;也可以是“第一天運的噸數”和“第二天運的噸數”，用加法：第一天運的噸數+第二天運的噸數=一共運的噸數。

通過反復聯想訓練，學會依據關聯的兩個數量聯想出問題，或者依據一個問題聯想到另外兩個數量，逐步熟練地掌握基本數量關系及三量之間的變化。

（三）敘述思路，掌握基本方法

古人云“言為心聲，言乃說，心乃思。”就是說：語言反映思維，語言與思維密不可分。在教學中培養學生有條理、有根據地表達解題思路，有利于對數量關系的深刻理解和靈活運用。

例如：合唱隊有女同學62人，是男同學人數的2倍，合唱隊一共有多少人？教師要引導學生敘述思路：根據“合唱隊有女同學62人，是男同學人數的2倍”，可以求出“男同學的人數”，用“女同學的人數÷2=男同學的人數”，再用“女同學的人數+男同學的人數=一共的人數”，可以求出“合唱隊一共有多少人？”算式是62+62÷2。這樣從條件出發分析、解決問題的方法就是“綜合法”，即從實際問題的已知條件出發，根據數量之間的關系，先選擇兩個已知數量，提出所能解決的問題;再把求出的數量作為新的已知條件，與其他的已知條件搭配，繼續提出所能解決的問題，這樣由因導果，直至推出所要解決的問題為止。

相反，也可以運用“分析法”從問題出發分析、解決問題，即是從所求問題出發，根據數量之間的關系，找出解決這個問題所需要的兩個條件，再把其中未知的條件作為新的問題，繼續找出解決這個新問題所需要的兩個條件，這樣執果索因，直至所需的條件全部找到為止。要求“合唱隊一共有多少人？”用“女同學的人數+男同學的人數=一共的人數”，由于男同學的人數沒有直接告訴我們，所以要先算，用“女同學的人數÷2=男同學的人數”，算式是62+62÷2。

讓學生經歷一系列口頭語言表達的演繹推理活動，加強了問題—條件—算式之間的聯系，既加深了解數量之間的關系，又促進學生掌握分析、解決問題的基本方法，從而有效提高邏輯思維和解決問題的能力。

（四）分析比較，正確推進理答

1.從運算的意義上分析比較

解決問題是以四則運算為載體，因此分析數量之間的關系必須以四則運算的意義作為思維的基礎。如：

（1）同學做游戲，一組5人，另一組6人，一共有多少人？

（2）同學做游戲，分成5組，每組6人，一共有多少人？

通過比較，看清這兩題敘述的事情和要求的問題都相同，但由于條件不同，所以解法也不同。第1題是把兩個數合并起來，用加法。第2題是求5個6相加是多少，用乘法。如果用加法列式，就要5個6連加。經過這樣分析，學生明白：這兩道題都是求總數，加法中的加數可以相同，也可以不同;而乘法解決問題是求相同加數的和。

2.從概念的理解上分析比較

有些概念，雖然只有一字之差，可含義大相徑庭，如不加以區別，很容易出錯。教學中，要經常將一些易混淆的概念設計成題組進行比較，仔細鑒別，弄清概念，明確數量關系。如：

3.從事理的敘述上分析比較

題目中所敘述事情的道理即為事理。如二年級教學“求比一個數多（或少）幾的數”，由于教材中的例題和開始練習的習題都是順敘的。部分學生造成了見多就用加法、見少就用減法計算的思維定式，結果當出現逆敘的題目時，就造成意識泛化，出現負遷移，即使到了高年級也不例外。因此要經常將這類順敘與逆敘的題目放在一起，進行對比分析，弄清題目里敘述的是誰跟誰比，誰多誰少，問題求的是什么數。

4.從結構的異同上分析比較

有些需要兩步計算的解決問題，給出的條件和要求的問題跟一步計算的解決問題極為相似，學生很容易將兩步計算的題目當作一步計算來解答。如：

（1）第一筐蘋果50千克，比第二筐多5千克，第二筐有多少千克？

（2）第一筐蘋果50千克，第二筐45千克，兩筐一共多少千克？

（3）第一筐蘋果50千克，比第二筐多5千克，兩筐一共多少千克？

這三題都有兩個條件和一個問題。但前兩題是一步計算的，后一題是兩步計算的。第（1）（3）題的條件完全相同，只是問題不同，第（2）（3）題的一個條件和問題完全相同，只是另一個條件不同，雖然解題的數量關系相同，都是用“第一筐的千克數+第二筐的千克數=一共的千克數”，由于第（3）題“第二筐的千克數”沒有直接給告知，所以要用兩步計算。通過分析比較，讓學生明白：凡一步計算的題目，給出的兩個條件都是直接知道的，而兩步計算的題目，解決問題所需要的兩個條件，其中的一個條件必定是間接的。另外，兩道連續性的一步計算解決問題可以合并成一道兩步計算解決問題，反之每一道兩步計算解決問題必定能分成兩道一步計算解決問題。在分析比較的過程中，學生認識和掌握兩步解決問題的結構，學生能從問題出發，認真分析已知條件中的直接與間接的關系，提高學生的分析、綜合能力。

（五）回顧反思，培養檢查習慣

《義務教育數學課程標準（2011年版）》十分強調“評價與反思”，通過“評價與反思”的環節，去關注問題解決的過程，總結問題解決的方法。如此能鍛煉學生挖掘和抓住事物本質的能力，培養學生“優化”的思想。從數學學習心理學的角度看，“評價與反思”本質上是一種元認知能力，它體現的是對自我思維的一種監控和調整，這在問題解決中尤其重要。教學中，首先要引導學生確立反思意識，明確檢驗的必要性;其次要教給學生一些具體檢驗的方法，如代入法、變換思路法、估算法、反證法等，教學中逐步滲透，以提高自我反思能力。

總之，提高學生解決問題的能力并非一朝一夕所能達成的，需要長期的、規范的、有意識的培養和訓練。