限制平均生存時間在區間刪失數據中的應用*

黃興輝 呂晶晶 楊紫荊 侯雅文 陳 征△

【提 要】 目的 針對區間刪失生存數據的分析研究，提出限制平均生存時間(restricted mean survival time，RMST)的估計和兩組比較檢驗。方法 利用修正EM算法進行迭代并得到生存率估計值，并基于此估計值構建RMST檢驗統計量求得P值，通過Monte-Carlo模擬驗證其統計性能。結果 本文提出的區間刪失生存數據中RMST檢驗法的I類錯誤在0.05附近波動，且其檢驗效能與現有常用方法Sun模型相當。結論 針對區間刪失生存數據的組間比較，本文提出RMST檢驗法不僅準確估計各組生存率，且通過計算RMST能夠直觀解釋組間差異大小并由此作出統計推斷，具有較好的統計性能，為臨床研究者和病人提供決策依據。

在醫學臨床研究中，通常需要對事件發生時間進行觀測，并進一步分析評價。當只知道事件發生在某一特定區間內，而不知道其確切的時間點時，將這類數據稱為區間刪失數據[1-3]，表示為T∈(L,R)，其中T表示個體的生存時間，L表示刪失區間的下界，R表示上界。目前對于區間刪失數據，現有一類廣義log-rank檢驗較為常用，例如Sun模型[4-5]，該方法基于單個區間內實際死亡數與理論死亡數的差值構造統計量，但是該類方法難以直觀解釋差異大小且可能會出現不收斂的問題；有研究[6-8]表明，限制平均生存時間(restricted mean survival time，RMST)表示從研究起始時間到一個特定時間點τ上的平均生存時間，即對應于時間點τ前的生存曲線下面積大小，并且針對該指標差值或者比值進行檢驗稱為RMST檢驗，能夠簡單描述生存狀態下平均生存時間的差異大小，在進行組間比較時應用廣泛[9-10]，特別是當風險率成比例假定不成立或者感興趣的事件數較少時，該指標能夠更加有效反映預后效果[11-12]。本文利用修正EM算法進行區間刪失數據的生存率估計，由此構造RMST檢驗統計量，對應提出區間刪失生存數據下的RMST檢驗法，通過模擬探索其穩健性和適用性并進行實例分析。

方法介紹

1.區間刪失生存數據中的RMST估計

(1)

對似然函數取對數，并對pj求偏導數得

i=1,…,n;l=j=1,…,m

(2)

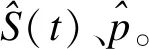
如圖1所示，對某戒毒中心的940名靜脈注射毒品患者經過戒毒治療后的HIV感染數據進行分析[14]，假設截止時間點為τ(最后一個觀察者的生存時間或者是最后一個事件者的死亡時間或者是某個給定的時間點，本研究取兩組中最大區間端點的較小值)，則限制性生存時間為X=min(T,τ)，由此可得X的期望，即限制性平均生存時間可以表示如下：

(3)

S(t)為生存函數，μ為區間[0,τ]上生存函數的積分，即對應于生存函數S(t)曲線下面積。

進一步計算E(X2)，即

E(X2)=E(T2|T≤τ)Pr(T≤τ)+τ2Pr(T>τ)

(4)

由于Pr(T≤τ)=1-S(τ)，則

(5)

故X的方差可以估計如下：

Var(X)=RSDST2=E(X2)-[E(X)]2

(6)

其中，RSDST為限制性標準差。

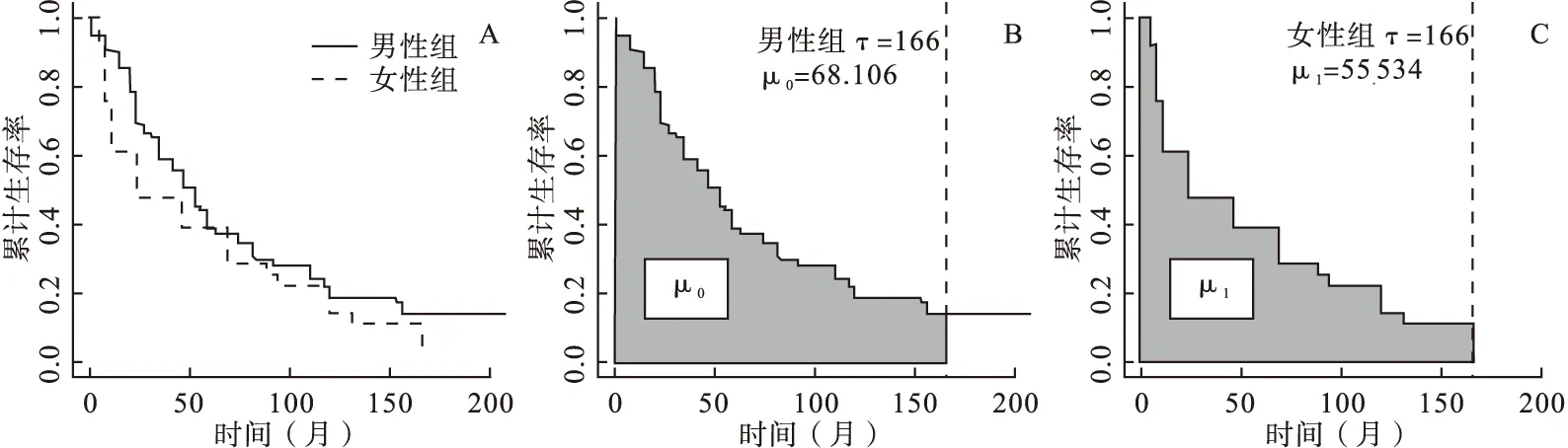
圖1 經戒毒治療后的HIV感染

圖1A為通過修正EM算法分別估計兩組的生存曲線圖，圖1B、圖1C陰影部分面積分別為兩組限制性平均生存時間的估計值，其中限制性平均生存時間及其方差的估計值如下：

(7)

(8)

2.區間刪失生存數據中的RMST檢驗法

比較兩組間生存率的差異，原假設是在任意時刻點t上，兩組對應的生存率相等，即H0:S1(t)=S2(t)，備擇假設H1:S1(t)≠S2(t)。根據限制性平均生存時間構造統計量，即在時間點τ上計算兩組限制性平均生存時間的差值Δ：

(9)

S0(t)，S1(t)分別為第一組、第二組的生存函數；μ0，μ1分別為第一組、第二組的限制性平均生存時間。

根據修正EM算法可得：

根據delta法進一步估計其方差：

(10)

在原假設、大樣本下該檢驗統計量服從t分布或正態分布[10]。

模擬研究

本文采用Monte-Carlo模擬來探索區間刪失生存數據中RMST檢驗法的檢驗效能和I類錯誤[5]，評價其穩健性和適用性。生存時間T：由參數為(α+βzi)的指數分布產生，zi是組別指示變量(zi=0表示對照組，1為試驗組)，即對照組、試驗組的生存時間T分別服從風險率為α、α+β的指數分布，且β表示試驗組與對照組風險率的差值。刪失區間產生：首先產生分別服從均勻分布(1,θ1)和(1,θ2)的相互獨立U1,U2，其中θ1,θ2是大于1的常數；然后定義U為U1四舍五入后的值，定義V為max(U1+U2,U+1)并取四舍五入后的值，由此產生刪失區間(U,V]；模擬通過θ1,θ2的不同取值控制左刪失(生存時間T小于刪失區間下限)、區間刪失(生存時間T位于刪失區間之間)及右刪失(生存時間T大于刪失區間上限)的比例。本研究設置α=0.2，n1=n2=30,100,200，循環次數設為1000次。

表1展示了不同樣本量、刪失百分比和β取值時兩種檢驗法的I類錯誤和檢驗效能，當α=0.2，β=-0.1，-0.05，0，0.05，0.1時，即固定第一組生存時間T服從風險率為0.2的指數分布，第二組生存時間T分別服從風險率分別為0.1，0.15，0.2，0.25，0.3的指數分布。表1第一列分別對應模擬數據中左刪失、區間刪失、右刪失所占比例，本文考慮了(1/3,1/3,1/3)和(1/4,1/2,1/4)兩種刪失率組合。從表1可見，當β=0時為I類錯誤：在不同刪失比例、不同樣本量組合下，兩種方法的I類錯誤都在0.05附近波動，RMST檢驗法在刪失比例為(1/3,1/3,1/3)且樣本量為(30,30)時I類錯誤偏小。當β≠0時為檢驗效能：樣本量為(30,30)時，兩種方法的檢驗效能交替較高；樣本量為(100,100)和(200,200)時，當β=-0.1和0.1，Sun模型較高，當β=-0.05和0.05，RMST檢驗法較高。

表1 I類錯誤和檢驗效能

*：α=0.2。

總體來說，本文提出的區間刪失生存數據中RMST檢驗法與常用的Sun模型均能較好控制I類錯誤，并且除了小樣本外具有較高的檢驗效能，具有較好的統計性能。

實例分析

對某戒毒中心的940名靜脈注射毒品患者經戒毒治療后的HIV感染數據進行分析[14]，該研究起始時間是戒毒治療的開始，終點事件定義為發生HIV感染，研究中心以月為單位定期檢查血清情況，由此確定在每個觀察區間內是否發生終點事件。因發生HIV感染的確切時間并不能被直接觀察到，即可將這些患者感染HIV看作區間刪失型數據；若患者在觀察期內未發生終點事件，則為右刪失數據。根據性別進行分組，男性組有759例患者，女性組有181例患者。

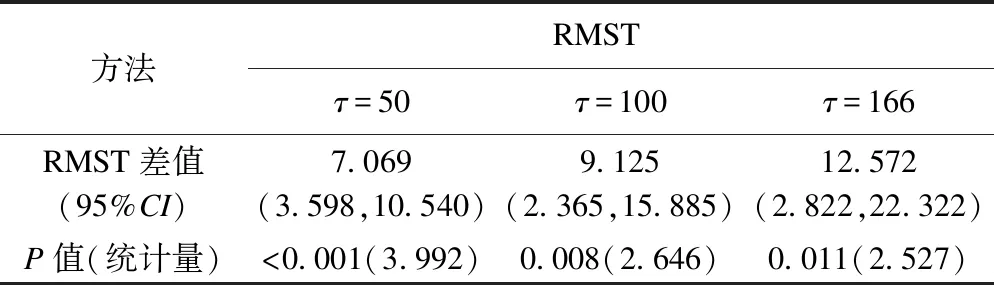
表2 RMST檢驗法的實例分析結果

*：Sunχ2=3.448,P=0.063。

由圖1和表2可見：當τ取兩組最大區間端點的較小值(即τ=166)時，在男性中限制性平均生存時間μ0=68.106個月(圖1B中生存曲線下面積值)，在女性中限制性平均生存時間是μ1=55.534個月(圖1C中生存曲線下面積值)，故男性與女性的限制性平均生存時間差值為12.572個月，且其對應的95%可信區間為(2.822,22.322)，RMST檢驗統計量z=2.527，P=0.011，提示在戒毒治療開始至第166個月，男性組、女性組的平均HIV感染時間有統計學差異，且男性較女性長12.572個月；假如研究者關心的時間點是截止到第50個月(即τ=50)時，男性組、女性組的平均感染時間分別為36.928、 29.859個月，其差值及95%可信區間為7.069(3.598,10.540)，z=3.992，P<0.001；同理，假如研究者關心的時間點是截止到第100個月(即τ=100)時，男性組和女性組的平均感染時間分別為54.721、45.596個月，其差值及95%可信區間為9.125(2.365,15.885)，z=2.646，P=0.008。對于Sun模型，χ2=3.448，P=0.063，該檢驗法只能給出兩組差異的整體性檢驗結果，即提示兩組HIV感染時間沒有統計學差異。

討 論

本研究結合修正EM算法，在區間刪失生存數據中進行RMST檢驗法的發展與應用。本文提出的RMST檢驗法既保證了生存率的準確估計，又對區間刪失生存數據中組間差異進行直觀闡述和比較；不管風險率是否成比例，該檢驗法均通過兩組生存曲線下面積差值構建統計量，能夠直觀反映在τ時刻前平均生存時間的差異大小，并做假設檢驗，在事件數較少時依然適用，為臨床研究者和病人提供平衡風險-成本-效益(risk-cost-benefit)并作出決策的依據。由上述實例分析結果可知，τ的選取對結果的影響較大。截止時間點τ需要在實驗設計階段就明確定義，并且其不同取值對應不同的限制性平均生存時間，從而導致檢驗結果有所不同。本研究實現了在區間刪失生存數據中RMST檢驗的拓展，并通過模擬驗證其能夠較好地控制I類錯誤同時具有檢驗效能，但尚未與其他現存檢驗方法進行全面比較。此外，本研究只考慮了兩組的情況，涉及多組的組間比較有待進一步推導和完善。