模擬產生具有相關關系的終點指標數據及R軟件實現*

張玲云 張曉敏 卓仁杰 劉麗亞△

腫瘤藥物療效的金標準評價指標為總生存期(overall survival,OS),但是應用該指標作為"最終"臨床研究終點會使整個研發周期延長、研發成本提高。實際工作中，常常考慮應用有效的短期替代終點代替總生存期作為腫瘤藥物療效評價的"最終"臨床研究終點。常見腫瘤臨床試驗替代終點包括腫瘤大小，無進展生存期(progression-free survival,PFS)，至疾病進展生存期(time-to progression,TTP)及無病生存期(disease-free survival,DFS)等[1-2]。目前，關于如何驗證替代終點是否能夠有效替代真實終點仍存在許多爭議，但是，毋庸置疑的是替代終點與總生存期具有強相關關系是替代終點有效的必要條件[3-4]。一項研究表明，2005年到2007美國食品藥品監督管理局(the U.S.Food and Drug administration,FDA)批準通過的53種腫瘤新藥中有9種(17%)腫瘤臨床試驗的研究終點指標為PFS[5]。由此可知腫瘤藥物臨床試驗研究當中不同結局變量間普遍存在相關關系[6]。因此，關于如何模擬產生具有相關關系的生存時間數據是腫瘤臨床試驗模擬研究亟待解決的問題之一。

本文介紹并討論了三種模擬產生具有相關關系生存時間數據的方法，并通過實例介紹其R軟件實現[7]。

方法與原理

1.基于Copula函數法

目前，快速發展的Copula理論是構建具有相關非正態變量聯合分布函數的有效手段之一，Copula函數實際上是一類將聯合分布函數與它們各自的邊緣分布函數連接在一起的函數，因此也有人將它稱為連接函數。Copula函數的提出最早可以追溯到1959年，SKlar通過定理形式將多元分布與Copula函數聯系起來[8]。

Copula函數種類很多，如Gaussian，t，Clayton，Frank，Gumbel，Plackett Copula等，其中由于Gaussian Copula函數可根據變量邊緣分布及相關系數矩陣唯一確定變量的聯合分布函數，故采用Gaussian Copula函數產生具有相關關系的生存時間數據可以根據實際情況設定相關系數ρ[9]。

以相關的二元分布為例介紹如何應用Gaussian Copula函數構建具有相關關系的二元非正態變量x1和x2的聯合分布函數。

(1)模擬產生樣本量為N相關系數為ρ的二元正態分布(Z1,Z2)，

(1)

(2)分別計算兩變量Z1和Z2的累積分布用U1和U2表示，

U1=Φ(Z1)

U2=Φ(Z2)

(2)

(U1,U2)表示具有相關關系的二元均勻分布，范圍分別為(0,1)。

(3)假定待估計具有相關關系的二元非正態變量X1和X2的邊際分布函數分別為，F1(·),F2(·)則

(3)

假定生存時間服從指數分布，同時考慮截尾時間變量，則根據Gaussian Copula函數模擬產生具有相關關系的生存時間變量的具體步驟如下，

(1)模擬產生樣本量為N相關系數為ρ的二元正態分布(Z1,Z2)；

(2)依次計算二元正態分布(Z1,Z2)每個變量的累積分布，用(U1,U2)表示，即二元均勻分布，范圍是(0,1)；

(3)生存時間服從指數分布，則生存時間X的分布函數及其反函數分別為F(t)=1-e-θt，F-1(t)=-ln(1-F1(t))/θ1。將U1看作是1-F1(t)代入變量分布函數的反函數估計生存時間X。同理，估計生存時間Y；

(4)模擬產生截尾時間變量C，C～Uniform[0,a]；

(5)根據上述步驟模擬產生的(X,Y,C)及公式Zx=min(X,Y,C),Zy=min(Y,C),δx=I(X≤min(Y,C))、δy=I(Y≤C)產生TTP(即Zx)與OS(即Zy)變量以及相應截尾變量，I表示指示函數。

例1 生成1000個相關關系為0.5的TTP與OS，要求TTP與OS的中位生存時間分別為2個月、4.5個月且截尾時間變量服從均勻分布[0,36]。

說明：題目設定的相關系數是Copula函數指定的二元正態分布相關系數，而非TTP與OS相關系數。

程序如下：

install.packages("mvtnorm")

library(mvtnorm)

n=1000 #樣本量為1000

corr=0.5 #相關關系為0.5

sigma=matrix(c(1,corr,corr,1),ncol=2) #相關系數矩陣

x=rmvnorm(n=n,mean=c(0,0),sigma=sigma) #模擬產生二元正態分布隨機變量

p1=pnorm(x[,1],mean=0,sd=1,lower.tail=TRUE,log.p=FALSE) #變量Z1的累積分布函數U1

p2=pnorm(x[,2],mean=0,sd=1,lower.tail=TRUE,log.p=FALSE) #變量Z2的累積分布函數U2，

TTP0=qgamma(p1,1,rate=log(2)/2,lower.tail=TRUE,log.p=FALSE) #TTP服從中位生存時間為2的指數分布

OS0=qgamma(p2,1,rate=log(2)/4.5,lower.tail=TRUE,log.p=FALSE) #OS服從中位生存時間為4.5的指數分布

censor=runif(n=n,min=0,max=36) #截尾變量censor服從均勻分布[0,36]

OS=pmin(OS0,censor) #實際的OS為OS0與censor的最小值

TTP=pmin(TTP0,OS0,censor) #實際的TTP為TTP0,OS0和censor的最小值

TTP_cen=(TTP0<=OS) #如TTP0小于等于實際的OS則認為疾病進展事件發生，表示疾病進展在死亡前、觀察截止前被觀測到

OS_cen=(OS0<=censor) #如OS0小于等于截尾時間則認為終點事件發生，表示死亡事件在觀察截止前被觀測到

Data_EX1=cbind(TTP,OS,TTP_cen,OS_cen) #最終生成的數據集

另上述程序假定生存時間均服從指數分布，如生存時間服從Weibull分布的，上述生成TTP0、OS0的步驟可修改為，

TTP0=qweibull(p1,1,2/log(2),lower.tail=TRUE,log.p=FALSE) #TTP服從中位生存時間為2的Weibull分布

OS0=qweibull(p2,1,4.5/log(2),lower.tail=TRUE,log.p=FALSE) #OS服從中位生存時間為4.5的Weibull分布。

2.混合指數模型法

腫瘤病人在死亡前常經歷數次疾病進展，如圖1所示，然而疾病進展后的死亡風險一般高于疾病進展前，因此構建產生生存時間數據模型時應充分考慮疾病發生發展機制。采用混合指數模型法分別模擬產生疾病進展前、后生存時間，不同階段的死亡風險可依據實際情況設定不同參數[10]。

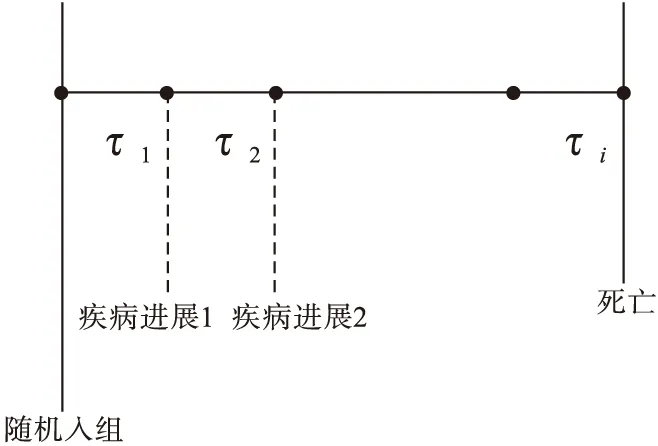
圖1 腫瘤患者疾病進展示意

(4)

如果k≠i則λi≠λk。

假定受試者只經歷一次疾病進展后死亡，即n=2時，t的概率密度函數可表示為:

(5)

則根據混合指數模型模擬產生具有相關關系生存時間數據的具體步驟如下:

(1)模擬產生樣本量為N，參數為λ1的指數分布，TTP；

(2)模擬產生樣本量為N，參數為λ2的指數分布，PPS；

(3)OS=TTP+PPS，則將步驟(1)與步驟(2)產生的模擬數據相加得到OS。

基于該法不能考慮受試者在疾病進展前發生死亡事件，Fleischer等人于 2009年對該法進行了改進[11]。首先，假定TTP與OS存在相關關系，TTP服從參數為λ1的指數分布。其次，引入X變量，表示未經歷疾病進展的患者從隨機化分組至死亡的時間，服從參數為λ2的指數分布，X～Exp(λ2)。由于TTP與X變量相互獨立，設定PFS=min(TTP,X)，則PFS仍服從指數分布，PFS～Exp(λ1+λ2)。最后，假定疾病進展后生存期(post-progression survival,PPS)仍服從參數為λ3指數分布，PPS～Exp(λ3)。因此，OS可表示為，

(6)

此時OS風險函數不再是一個常量，隨著疾病進展而改變。一般來講，疾病進展后的風險率高于進展前(λ3>λ2，即疾病進展前死亡風險為λ2，疾病進展后死亡風險為λ3)。基于上述假定，PFS與OS的相關關系為:

(7)

在其他參數不變前提下，隨著λ1或λ2的增加PFS與OS的相關關系下降，隨著λ3的增加PFS與OS的相關關系增加，見圖2。

圖2 PFS與OS在不同參數組合下相關關系情況(lamda2=1)

*：lamda1，表示TTP服從參數為lamda1的指數分布；lamda2，表示未經歷疾病進展患者從隨機化分組至死亡的時間服從參數為lamda2的指數分布；lamda3，表示PPS服從參數為lamda3的指數分布；correlation表示PFS與OS相關系數。

例2 模擬產生1000個具有相關關系的PFS與OS數據，要求TTP、PPS的中位時間分別為5個月及15個月，未經歷疾病進展患者的中位生存時間為7.5個月。

程序如下：

n=1000 #樣本量為1000

rate1=log(2)/7.5 #未經歷疾病進展患者的死亡風險函數

rate2=log(2)/5 #TTP的風險函數

rate3=log(2)/15 #PPS的風險函數

x=rexp(n,rate1) #模擬產生未經歷疾病進展患者的死亡時間

ttp=rexp(n,rate2) #模擬產生TTP

pfs=pmin(ttp,x) #模擬產生PFS

pps=rexp(n,rate3) #模擬產生PPS

os=pps+pfs #模擬產生OS

cor(pfs,os) #估計PFS與OS相關關系

3.混合Bayes模型法

Michael等人于2002年提出一種能夠精確模擬產生具有相關關系的多元分布新方法，稱為混合Bayes模型法[12]。該法應用Bayes思想，易于推廣，其本質是根據后驗分布模擬產生與先驗具有相同邊際分布的樣本，兩個邊際分布的相關關系由似然函數決定。

假定隨機變量X1的先驗分布為

g(x1;θ)

(8)

參數θ表示多維變量；在X1=x條件下，根據抽樣分布K|(X1=x)獲得樣本，構建似然函數可表示為

h(k|x1;η)

(9)

將公式(8)與公式(9)相乘，得變量X1和K聯合分布

j(x1,k;θ,η)=g(x1;θ)h(k|x1;η)

(10)

對X1積分得K的邊際分布

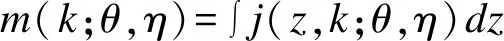
(11)

給定K=k條件下，估計X2的后驗分布

p(x2|k;θ,η)=j(x2,k;θ,η)/m(k;θ,η)

(12)

變量X1與X2有相同的邊際分布，X2分布為不同后驗分布的加權平均，準確地再現了先驗分布。假定生存時間滿足Gamma分布，則變量X1與X2的邊際分布均為Gamma分布。

應用混合Bayes模型法模擬產生具有相關關系的生存時間變量的具體步驟如下：

(1)確定先驗分布X1～Γ(a,b)，根據先驗分布模擬產生X1，樣本量為N;

(2)由于Poisson分布的共軛先驗分布是Gamma分布，因此條件抽樣分布為K|(X1=x)～Poisson(τx)，據此分布抽樣獲得樣本量為N的K；

(3)根據先驗以及抽樣獲得的K估計后驗分布，X2～Γ(a+k,b+τ)；

(4)根據每個后驗分布依次模擬產生X2，據此獲得的二維隨機變量(X1,X2)具有相關關系且邊際分布均為Gamma分布，相關系數為

(13)

(5)模擬產生截尾時間變量C，C～Uniform[0,a]；

(6)根據上述步驟模擬產生的(X1,X2,C)及公式Zx1=min(X1,X2,C),Zx2=min(X2,C),δx1=I(X1≤min(X2,C))，δx2=I(X2≤C)產生TTP(即Zx1)與OS(即Zx2)變量以及相應截尾變量，I表示指示函數。

例3 模擬產生1000個相關系數為0.78的TTP與OS，要求TTP服從指數分布中位時間為5個月。

說明：依據實際情況需要模擬產生生存時間數據需考慮截尾時間。本文介紹混合Bayes模型法模擬產生截尾時間變量的步驟同例1一致，故R程序一致，同時由于考慮截尾時間將會影響TTP與OS的相關關系，故本例未考慮截尾時間變量。本例模擬數據產生后可評估TTP與OS的相關系數與設定參數是否一致，從而檢驗模擬過程是否正確。

程序如下：

n=1000 #樣本量為1000

shape1=1 #形態參數為1的Gamma分布是指數分布

rate1=log(2)/5 #尺度參數

prior=rgamma(n,shape1,scale=1/rate1) #先驗分布為指數分布，即TTP

tau=0.5 #Poisson分布的τ設定為0.5

lamda=data.frame(tau*prior) #估計條件分布K|(X1=x)～Poisson(τx)參數

likelihood=rpois(n,lamda[,1]) #據條件分布抽樣獲得K，樣本量為1000

shape2=data.frame(shape1+likelihood) #根據先驗形態參數以及抽樣獲得的K估計1000個后驗分布的形態參數

rate2=1/(1/rate1+tau) #依據相關關系公式估計后驗分布的尺度參數

posterior=rgamma(n,shape2[,1],scale=1/rate2) #據1000個后驗分布抽樣獲得1000個后驗樣本，即OS

cor(prior,posterior) #估計TTP與OS相關系數

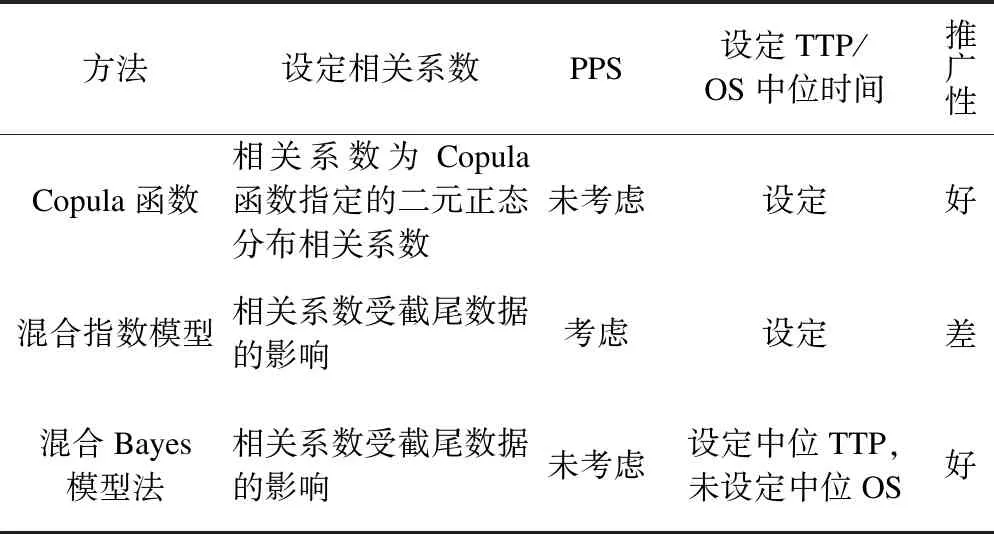
表1 三種模擬產生具有相關關系生存時間數據方法的優缺點

*：PFS，progression-free survival，無進展生存期；TTP，time-to progression，至疾病進展生存期；PPS，post-progression survival，疾病進展后生存期。

討 論

關于如何模擬產生具有相關關系的生存時間數據廣泛應用于研究與實踐領域，主要用于評估統計分析方法的統計學性能。本文介紹了三種模擬產生具有相關系數生存時間數據的方法，其相關系數參數均能設定，但是由于截尾數據的存在，模擬設定的相關系數將會受到影響，且隨截尾變量均勻分布上限的縮短而降低。

在實際工作中應用三種方法產生模擬數據時需注意：(1)Copula函數法設定的相關系數是二元正態分布相關系數而非生存時間相關；(2)混合指數模型法可以控制PPS的長短，如果模擬試驗研究考慮該變量作為研究的變化參數時，則只能采用該法產生模擬數據；(3)混合Bayes模型法不能設定中位生存時間；(4)Copula函數法和混合Bayes模型法除能模擬產生具有相關關系的生存時間變量外，也可推廣應用至其他分布類型數據的模擬產生，但是應用混合Bayes模型法要求具有相關關系的先驗與后驗分布類型一致。

本研究為建立一套科學、可行、又可操作的產生具有相關關系的模擬數據的方式提供依據，進而解決科研工作者在生存資料模擬研究中關于產生模擬數據的困惑。本研究的局限性在于產生截尾時間數據的方式均基于均勻分布且截尾類型僅考慮右側截尾情況，因此在實際工作中產生模擬數據的方式需依據實際情況而定。