四輪轉向系統二自由度模型的建立與仿真分析
于霞 孟憲皆
山東理工大學交通與車輛工程學院 山東省淄博市 255000
四輪轉向(4WS),是指在汽車轉向時四個車輪同時發生偏轉四輪轉向系統在低速時,可以減小汽車的最小轉彎半徑,提高汽車的靈活性與機動性;高速時,具有較快的響應速度,通過合理控制后輪的偏轉角,又能提高汽車的操穩性和行車安全性[1]。
1 模型的簡化
為了使問題便于分析,我們做以下假設,將其簡化為二自由度模型。(1)汽車做等速直線運動。(2)直接以前、后輪轉角作為輸入。(3)該模型的汽車不具有懸架,即將簧載和非簧載質量看成一部分。(4)忽略地面切向力所導致的輪胎側偏特性變化。(5)空氣動力的作用不在考慮范圍之內。(6)忽略輪胎因載荷的變化而引起輪胎的變化。(7)輪胎側偏特性始終為線性。(8)汽車左右對稱。(9)不考慮回正力矩的影響。得到只具有y軸上的側向運動和z軸上的橫擺運動的二自由度轉向系統模型。
2 運動微分方程的建立
對模型進行受力分析和運動分析(如圖1所示),依據牛頓第二定律列出二自由度模型的運動微分方程如式(1)所示。其中前后輪所受地面側向反作用力分別為1YF、2YF ,前后輪所輸入的轉角分別為1δ、2δ,前后輪的側偏角分別為1α、2α,汽車的橫擺角速度為rω,β為整車的質心側偏角,汽車質心處的速度在x軸和y軸上的分量分別為u、v。

圖1 四輪轉向系統二自由度模型
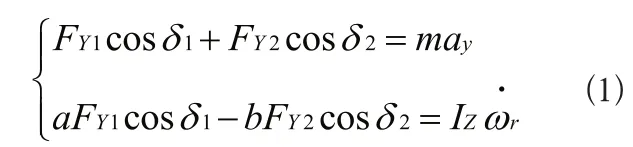
其中根據輪胎的側偏特性有:

根據幾何關系及運動分析可得:
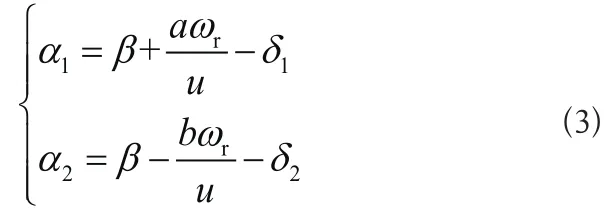
在轉角很小的情況下,即δ1、δ2很小,故有 c osδ1≈1,cosδ2≈1,質心側偏角β也。將上述關系及式(3)和式(2)代入式(1),得到四輪轉向系統的二自由度模型的運動微分方程如式(4)所示。
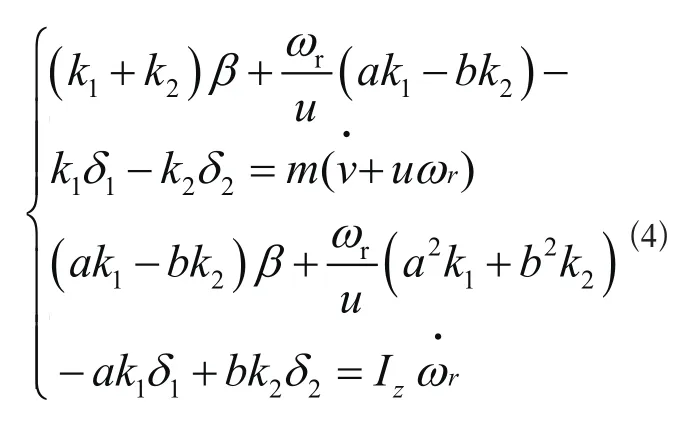
將式(4)化為狀態方程如式(5)的形式,以更方便的研究輸入變量和狀態變量的關系。A、B、C、D均為常系數矩陣,設狀態變量
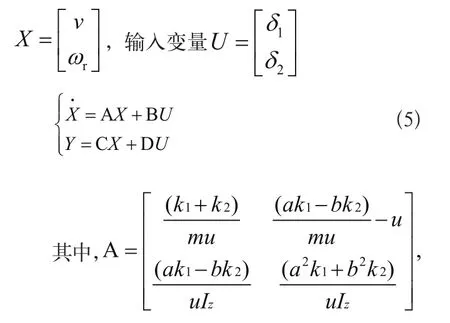

式(4)主要用于動力學特性的理論分析,式(5)主要用于仿真分析。當時20δ=,該模型就可以轉化為傳統轉向汽車二自由度轉向模型。
3 四輪轉向系統二自由度模型的仿真分析
運用MATLAB/Simulink對模型進行相應的仿真分析,構建仿真模型(如圖2所示),參數如表1所示。

表1 仿真分析所用汽車的相關參數
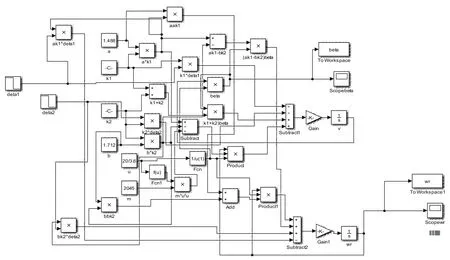
圖4 低速和高速下質心側偏角響應曲線
4 低速和高速下的仿真對比分析
在1s時,給前輪和后輪同時輸入相同的角階躍信號 δ1=δ2=0.1rad 。設v1=20km/h v620== km/h,做相應的橫擺角速度(如圖3所示)和質心側偏角響應曲線(如圖4所示),來分析四輪轉向系統在低速狀態和高速狀態下的轉向特性。
由圖3可知,當汽車處于高速狀態下同相位轉向時,其橫擺角速度要小于低速時的逆相位轉向。對比兩輪轉向系統,在低速狀態下差別不大;但在高速狀態下,四輪轉向系統有著較小的超調量和較短的穩定時間。因此四輪轉向系統高速下的同相位轉向對汽車的操縱穩定性是十分有利的。

由圖4可知,無論處于高速還是低速狀態,當角階躍信號輸入時,質心側偏角先迅速增大,達到峰值后,再迅速減小,最終趨近于零。這是因為后輪轉向產生了一個后軸側偏角,該側偏角與前軸側偏角相抵消,故整車的質心側偏角基本為零[2]。質心側偏角為零,即說明汽車的側向速度為零,即無側向運動,此時具有較好的操穩性。而兩輪轉向系統轉向時,質心側偏角往往不趨于零,而是趨于某一定值。由此可見四輪轉向系統在汽車的操縱穩定性方面具有兩輪轉向系統不可相媲美的優越性[3]。

圖3 低速和高速下橫擺角速度響應曲線

