弧形閘門流激振動功率譜設計及時域反演

李斯　吳思遠　王正中

摘要：針對現有弧形閘門流激振動功率譜設計欠缺，影響弧門動力分析及進一步減振控制的問題，在水流特性和實測脈動壓力分析基礎上利用優化思想和信號處理技術，以現有實測水頭與動水壓力對應關系及所選自回歸滑動平均模型（ ARMA）參數取值范圍為約束條件，建立了符合實測荷裁要求的功率譜模型和時域脈動荷裁反演方法。通過與現有設計方法進行對比，驗證了方法的有效性，結合工程實例給出了相應設計功率譜和隨機脈動壓力時程曲線。

關鍵詞：弧形閘門;流激振動;參數振動;功率譜;時域反演

中圖分類號：TV34

文獻標志碼：A

doi：10. 3969/j .issn.1000- 1379.2019.06.028

現有閘門動力分析多從結構自振特性和外界動荷載激勵兩個方面人手，研究方法主要有原型觀測試驗、物理模型試驗和數值分析等。在原型觀測方面，我國科研院所針對三峽、葛洲壩、劉家峽等幾十個工程做了相關工作，獲得了水流脈動壓力、自振頻率、阻尼比、振型及結構響應等動力分析參數，對于開展水彈性縮尺試驗及參數化數值模擬具有十分重要的意義，但受限于現場條件，所得樣本少[1]。水彈性試驗雖最為直觀，但其相似準則至今難以滿足（如尺寸效應、邊界條件等），實測值在某些指標上甚至存在數量級的差別。流場脈動壓力模型的不確定，使得有限元分析多限于模態分析獲取自振頻率，通過與水流脈動頻率比較，判斷結構的安全性，但缺乏全啟閉周期脈動水流作用下閘門結構的動力響應分析。

隨著信息和仿真技術的發展，有限元模擬無論在前期設計、優化，還是在后期分析、校核中均愈發重要。參考地震、風振和軌道等隨機過程可以發現，根據不同地形、高程等環境因素均可得到較為適當的功率譜密度（ PSD），進而模擬時域下隨機過程。而在流激振動中相應工作還遠遠不足，因此需要針對以往大量試驗數據進行統計分析，明確脈動荷載隨水頭、閘門開度的規律性變化，獲得設計功率譜，在此基礎上采用適當的反演方法獲得時域下脈動隨機過程。

1 功率譜模型搭建

從機理角度講，水流脈動在時間和空間上具有明顯的不確定性，是典型的隨機過程，但大量研究表明，恒定流動條件下，一般可將水流脈動視為高斯過程。在實際泄流時流動條件是非恒定的，水流脈動荷載應作為非平穩高斯過程處理，但在一定開度、一定時段內流動條件基本不變，仍可將其視為平穩高斯過程。這一隨機過程在工程上常用功率譜密度來描述。根據大量原型和模型試驗資料可知，水流脈動主頻率在1-20Hz范圍內變化，其中有48.35%在1-10 Hz之內，超過20 Hz的極少[2]。隨著閘門開度的增大，脈動壓力優勢頻率呈增大趨勢，主頻范圍也在增大[3-4]。同時，根據吳杰芳等[5]、嚴根華等[6]研究，脈動壓力主頻間存在倍率關系，且往往與閘門結構低頻較為接近。而脈動壓力隨閘門開度的增大而增大，最大均方值不超過作用水頭的20%，大多為2% - 10%。在實測功率譜中隨頻率增大，主峰呈一致減小趨勢。結合文獻[7]參數振動分析，在考慮最危險設計工況時，除共振外還應包含亞諧波參數共振及二階參數共振情況，由此可以設計最危險工況流激振動功率譜。其最危險工況為最小水流脈動頻率與支臂二階參數共振重合，第二脈動主頻與閘門基頻重合，第三脈動主頻與支臂亞諧波參數共振重合，進而功率譜峰值根據作用水頭及實測脈動荷載進行反饋調節。此處根據上述分析假定：①最大隨機脈動壓力水頭不超過作用水頭的20%：②二階參數共振，激發條件更為苛刻.故令第一脈動頻率與第二脈動頻率在功率譜中峰值相等，且大于第三脈動頻率。

2 時域反演模擬及功率譜設計

在設計過程中，需通過時域脈動荷載調整初始功率譜密度。但功率譜中僅包含脈動荷載的相關函數、均方值及能量信息，缺少幅值、相位信息，無法直接進行時域轉化，故需要采用信號處理技術進行功率譜反演，實現隨機過程的時域模擬。現有高斯平穩隨機過程的時域模擬方法，主要分為諧波合成法（ WAWS）和線性濾波法（ CAWS）。其中諧波合成法核心思想是采用離散法逼近目標譜，其算法簡單直觀、理論嚴密，但存在計算效率低下的問題。而線性濾波法則是將隨機過程x（n）抽象為由白噪聲ω（n）激勵的某假定系統，經積分變換擬合出時域響應，該方法靈活高效，應用更為普遍，但回歸模型及相應階數的選取帶有主觀性，精度較低[8]。

本文結合兩種時域模擬方法的優勢，以線性濾波器為模型結合諧波合成法中逼近思想，對系統函數進行參數優化設計，并根據一定算法改進模型階數選取的主觀性。這一方法提高了線性濾波器的精度，同時彌補了諧波合成法中計算效率低的不足。而在線性濾波器中自回歸滑動平均模型（ ARMA）是自回歸模型（AR）和滑動平均模型（MA）的結合，兼具兩者的優勢。

2.3 優化方案

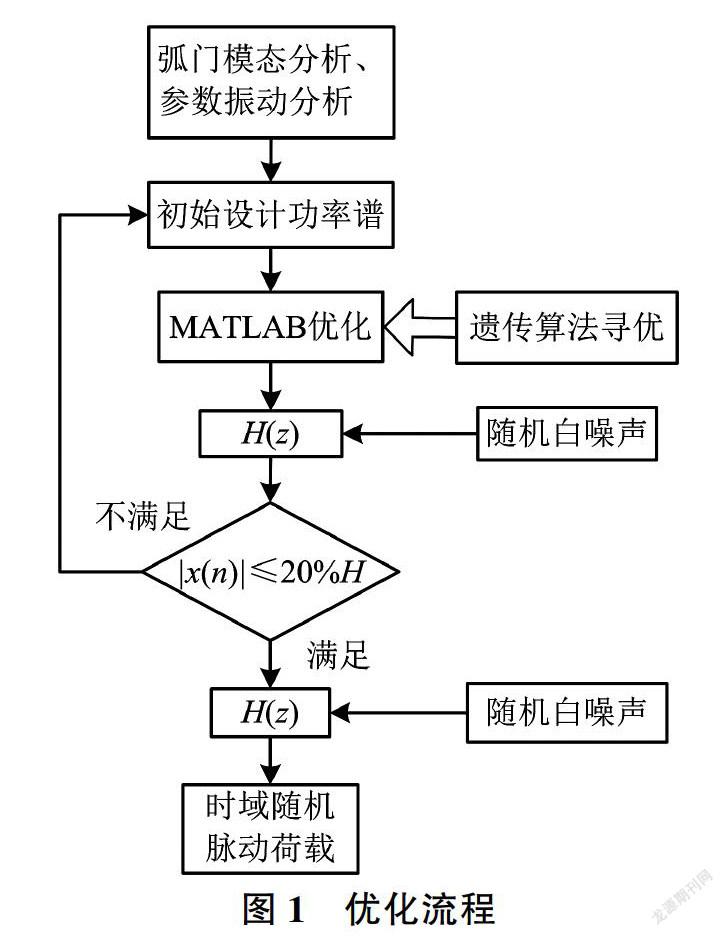
根據弧形鋼閘門自振頻率及參數振動分析結果給出最危險工況理想設計譜脈動頻率點，進而在MATLAB中采用遺傳算法進行全局濾波器參數優化，以此構建濾波器系統函數。通過輸入隨機白噪聲判斷是否滿足時域荷載范圍，若不滿足，則調整功率譜密度，按上述循環最終確定設計功率譜密度及時域隨機脈動荷載。優化流程如圖1所示。

3 對比驗證

以楊世浩[9]研究的功率譜為例，優勢頻率設計與本文設計方法有一定區別，文中第一主頻接近弧門主框架基頻，功率譜峰值最大，二、三主頻為第一主頻的倍頻，峰值一致遞減，其中并未考慮參數振動的影響，設計功率譜如圖2所示。

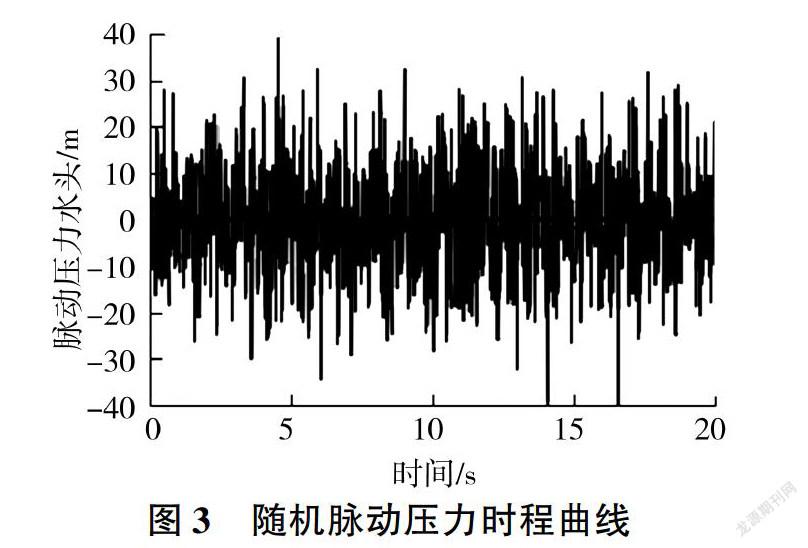
根據上述時域反演方法，模擬隨機脈動壓力（水頭）時程曲線如圖3所示，為驗證模擬的準確性，進行功率譜轉換，分析結果見表1。

由圖3和表1可知，通過本文功率譜反演方法可以得到滿足設計功率譜要求的脈動壓力時程曲線，表1模擬譜中非主峰值存在的偏差可以通過加密頻率取樣點來消除。該優化方案同樣適用于速度及位移功率譜的反演模擬。

4 設計實例

以某高水頭（設計水頭80 m）弧形鋼閘門的主框架平面內振動為例，計算模型如圖4所示。構件截面尺寸如圖4（b）所示，主梁采用“工”字形截面，彎曲平面內的慣性矩Ixl= 1.235×10 m ，單位長度質量m=430 kg/m;支臂采用箱形截面，彎曲平面內的慣性矩Ix2= 2.319xl0 m ，單位長度質量m= 386 kg/m;彈性模量E= 210 GPa[l0]。

根據弧門主框架模型參數，在ANSYS中利用BEAM189建模，得到結構前5階自振頻率，見表2。

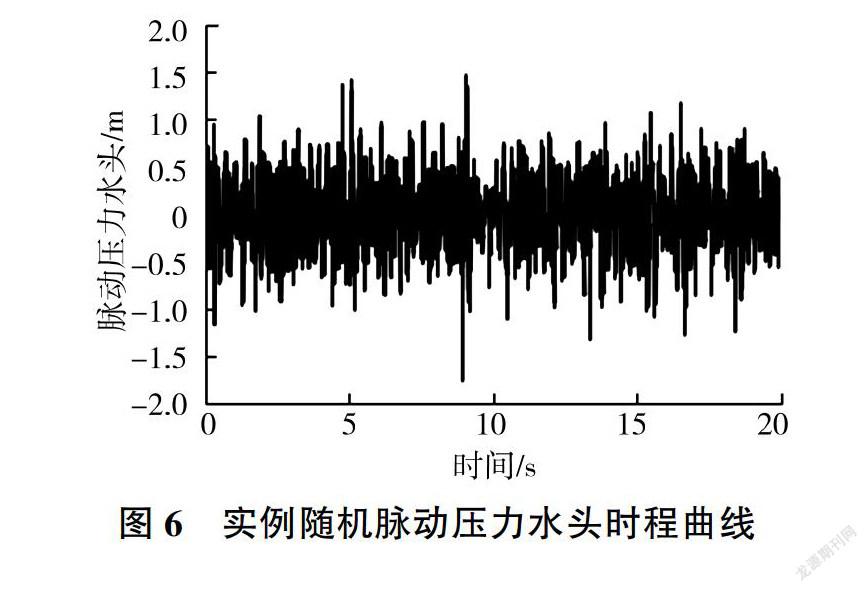
根據功率譜設計原則，脈動壓力水頭不超過16m，平面框架基頻為10.31 Hz，考慮參數振動二階參數共振及亞諧波參數共振設計功率峰值，分別為5.15、10.31、20.62 Hz。根據上述優化流程，得到理想設計功率譜及相應模擬隨機脈動壓力水頭，見圖5、圖6。

5 結語

本文在現有實測數據和統計分析結果的基礎上，結合弧門振動特性搭建了流激振動功率譜模型，進而選用自回歸滑動平均模型進行功率譜設計和時域反演。通過對比分析驗證了該方法的有效性，并將其應用于設計實例，為進一步開展弧門動力優化設計及減振控制提供了隨機脈動荷載。

參考文獻：

[l]李火坤，弧形閘門流激振動特性及其結構優化研究[D].天津：天津大學，2004：4-7.

[2]章繼光，我國閘門振動研究情況綜述[J].水力發電，1985，11（1）：38-44.

[3] 趙蘭浩，駱鵬.大型水工弧形鋼閘門流激振動物理模型：數值模型計算分析[J].水電能源科學，2017，35（12）：173-177.

[4] BRUSEWICZ K，STERPEJKOWICZWERSOCKIW，JANKOWSKIR. Modal Analysis of a Steel Radial Cate Exposed toDifferent Water Levels[J].Archives of Hydro-Engineeringand Environmental Mechanics， 2017， 64（1）：37-47.

[5]吳杰芳，張林讓，陳敏中，等，三峽大壩導流底孔閘門流激振動水彈性模型試驗研究[J].長江科學院院報，2001，18（5）：76-79.

[6] 嚴根華，陳發展，溢流壩表孔弧形閘門流激振動原型觀測研究[J].水力發電學報，2012，31（2）：140-145.

[7]

LIU J L，WANC Z Z，FANC X， et al.Dynamic InstabilityMechanism and Vibration Control of Radial Cate Arms[J].Applied Mechanics and Materials， 2011， 50（1）：309-313.

[8]李錦華，李春祥，土木工程隨機風場數值模擬研究的進展[J].振動與沖擊，2008，27（9）：116-125.

[9]楊世浩，水工弧形閘門流激振動脈動壓力的時域模擬[J].武漢理工大學學報，2004，26（8）：52-54.

[10] 吳思遠，王正中，王岳，等，基于Isight - MSC Patran/Nastran聯合仿真的弧形閘門動力模型修正[J].振動與沖擊，2018，37（19）：70-76.

【責任編輯張華巖】