基于軌跡數據的交叉口排隊長度計算方法

魏 然

（北方工業大學城市道路交通智能控制技術北京市重點實驗室，北京 100043）

1 背景和意義

1.1 背景

隨著城市交通的擁堵問題越來越嚴重，如何提高信號控制交叉口的運行效率成為解決交通擁堵的關鍵。交叉口的排隊長度是評價交叉口運行效率的重要指標之一，對交通信號優化、交通誘導、交通運行狀態評價均有相當重要的作用。

基于可探測車輛的軌跡數據，交通工作研究者開發了一系列新的方法來估計信號交叉口的排隊長度。在Comert[1]發表的開創性論文中，考慮到可探測車輛的穿透率和排隊長度的分布，最后一輛可探測車輛在排隊中的位置僅對逐周期排隊長度估算是有效的；還分析了不同情況下，不同穿透率的可探測車的估算精度。

Comert[2]通過考慮可探測車輛進入隊列的時間，將其工作擴展到空間和時間維度。2013年，Comert研究了停車線檢測數據的影響 （Comert，2013a）[3]，并提出了另一個簡單的分析模型 （Comert，2013b）[4]。王鈺等[5]引入了“消散延誤”概念，利用估計模型與車輛的“消散延誤”數據，實現交叉口每個周期的排隊長度及時估計。

1.2 意義

大多數現有文獻都集中于逐周期估算上，因此，需要可探測車輛的滲透率和隊列長度分布的先驗信息。然而，目前的方法難以在實際情況中實施。盡管Wong等[6]最近的一項研究提出了一種僅基于可探測車輛軌跡數據的新方法，但該方法不能處理某些隊列為空的情況。本文為了克服上述障礙，在更一般的框架中提出一系列方法。當車輛在交叉口停車時，由于車頭時距的經驗值通常在7.5 m/輛左右，因此可以大致推斷出最后一輛可探測車前方的車輛數。盡管最后一輛可探測車后方的車輛數量仍然未知，但不完整的信息可能為估算交叉口排隊長度提供了一個機會，這里僅通過隨機獲取的兩輛可探測車輛的停車位置來估計總的排隊長度，進而了解當前道路的交通需求。這個方法已經通過Vissim仿真驗證，可以較為準確地估算交叉口處的排隊長度。

2 問題描述

當車輛因為信號燈而停在交叉路口時，排隊中的一些車輛可能是可探測車輛，車端的GPS設備能夠記錄其軌跡。假設可探測車輛的軌跡數據是周期循環采集的，從軌跡上可以很容易地得到可探測車在隊列中的位置，從軌跡數據中很容易推斷出的內容l1，l2，l3，l5，l6，l8部分可見，因為隊列中有可探測車輛，l4，l7和l9是隱藏的，因為沒有可探測車輛，分別用Lobs和Lhid表示 （部分） 可觀測隊列的總長度和隱藏隊列的總長度。在第i個周期中，如果可以觀察到隊列，則分別用Si和Ti表示第一個和最后一個可探測車輛的位置。觀測過程如圖1所示。文中的一些符號總結如表1所示。

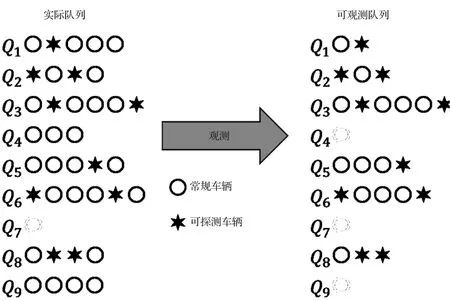
圖1 觀測過程

表1 符號

3 估算排隊長度

本文的方法基于這樣一個事實，即預期可探測車輛將等量分離常規車輛，這些估算值只需要每個周期中停止的可探測車數量以及隊列中第一個和最后一個可探測車輛的停止位置，所有這些都可以從軌跡數據中提取，因此，估算值是常數。

3.1 估算1：第一輛可探測車的停止位置

定理一：

給定任意整數ni≥1，給定Ni=ni，在第i個周期有：

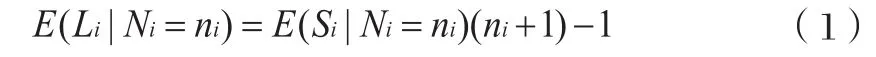
然后，根據上面的結果，定理一指出，給定可觀測隊列中可探測車的數量，可從第一個可探測車的預期停車位置獲得預期隊列長度，根據定理一，給定每個周期內可探測車的數量，可觀測隊列的預期總長度可表示為：

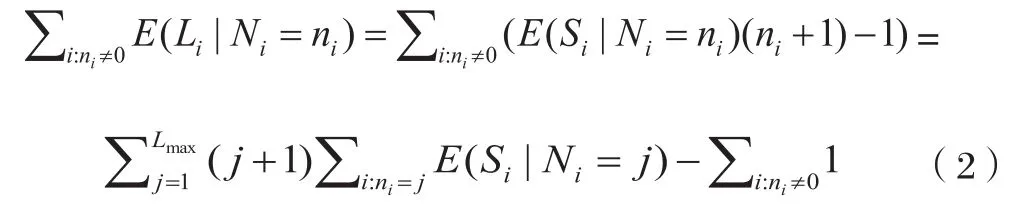
因此，假設第i個周期Si=si， i∈{1，2，…，C}，對于預期值（Si|Ni=j）， j≥1，可以用樣本均值代替，Lobs可以估計為：

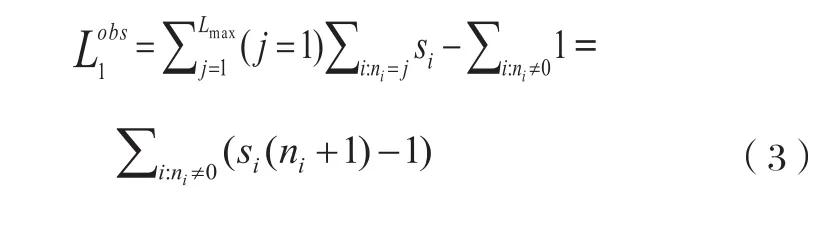
3.2 估算2：最后一輛可探測車輛的停車位置

定理二：

對于任意整數ni≥1，假設在第i個周期時Ni=ni，則：

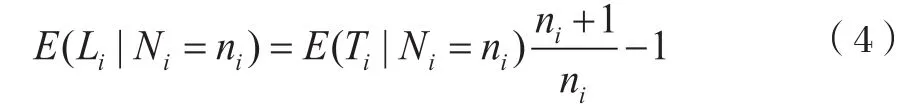
定理二指出，給定一個可觀測隊列中可探測車輛的數量，可以從最后一輛可探測車輛的預期停車位置獲得預期隊列長度。根據定理二，給定每個周期內可探測車輛的數量，可觀測隊列的預期總長度可以表示為：

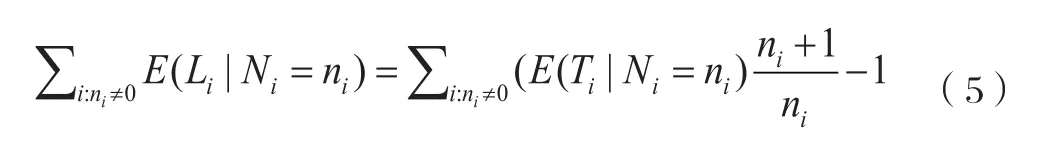
遵循方法一的類似推倒，假設第i個周期Ti=ti， i∈{1，2，…，C}，對于預期值E（Ti|Ni=j）， j≥1，可以用樣本均替代，Lobs可以估計為：

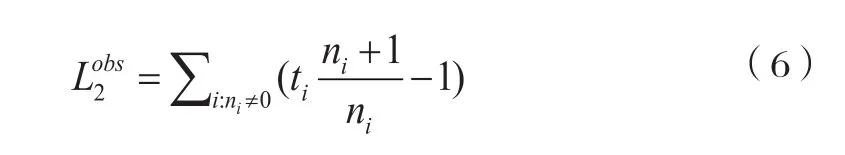
3.3 估算3：第一輛和最后一輛可探測車輛的停車位置

定理三：

對于任意整數ni≥1，假設在第i個周期時Ni=ni，則：

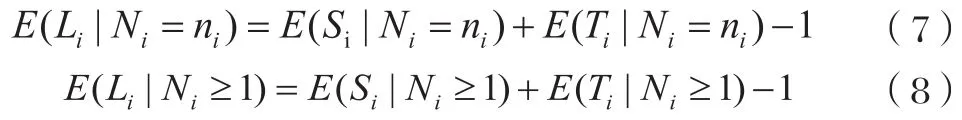
定理三指出，給定一個可觀測隊列中可探測車輛的數量，可以從第一輛和最后一輛可探測車輛的預期停車位置獲得預期隊列長度。根據定理三，給定每個周期內可探測車輛的數量，可觀測隊列的預期總長度可以表示為：

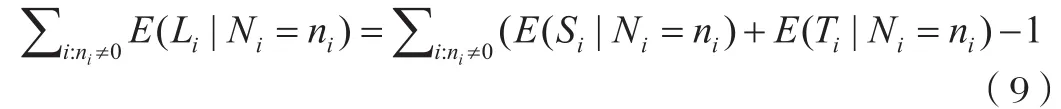
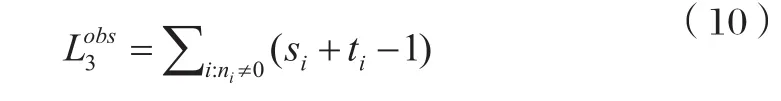
背后的機制是直觀的，以圖2為例，第k個周期中的排隊與第j個周期中的排隊相反，這就意味著第j個周期中最后一輛可探測車輛后面的車輛數等于第k個周期中第一輛可探測車輛前面的車輛數。由于對稱性，這兩個隊列具有相同的發生概率，因此，即使一個周期中最后一輛可探測車輛后面的車輛數未知，只要數據量足夠，缺失的車輛數量可以通過另一個周期中第一輛可探測車輛前面的車輛數量進行補償。

圖2 最后一輛可探測車后方的車輛由其他隊列補償

4 仿真驗證

4.1 交叉口現狀

如圖3，選取燕郊地區京榆大街與燕靈路交叉口，在Vissim中畫出路網并填寫交通數據，通過實地檢測數據獲得的該交叉口西進口道直行方向的流量為1 800 pch/h，通過現場調查得到的信號配時方案如圖4所示。本次驗證選取西進口道直行方向交叉口車輛排隊長度作為計算指標，采用9個不同的隨機種子進行仿真，通過Vissim中排隊長度檢測器測得的實際排隊長度值如表2所示。

圖3 京榆大街與燕靈路交叉口

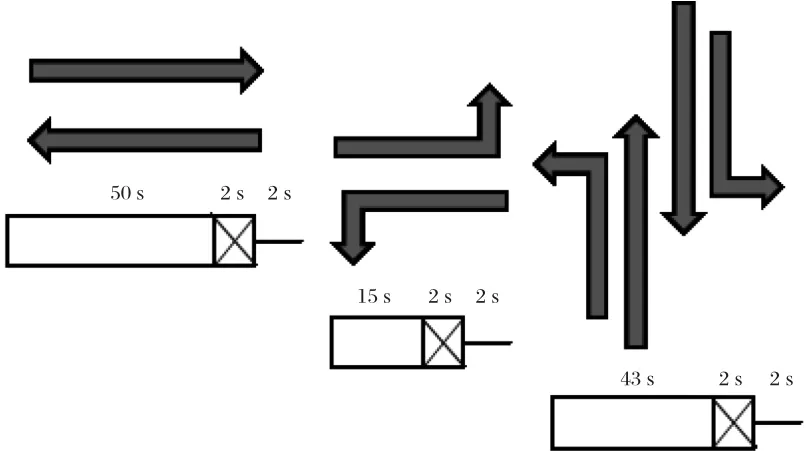
圖4 交叉口信號配時方案

表2 西進口道直行方向實際排隊長度值 /m

4.2 基于軌跡數據計算排隊長度

為了得到車輛的軌跡數據，采用c#進行二次開發，具體流程如圖5，在路段起點處設置檢測器，隨機讀取經過檢測器的車輛作為可探測車輛，繼續跟蹤記錄到的車輛的速度，當車輛速度為0時證明此可觀測車輛正處于在交叉口排隊的狀態，輸出此時車輛的位置，在不同隨機種子情況下重復試驗。

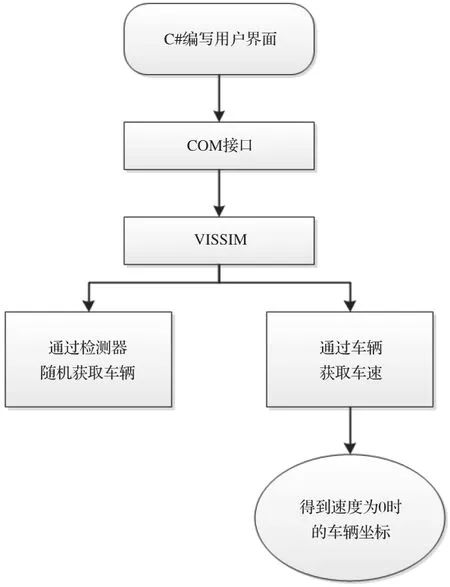
圖5 軌跡數據獲取流程圖

將得到的車輛位置數據代入方法三的公式 （10），奇數位置的數據代表最后一輛可探測車輛的停車位置，偶數位置的數據代表第一輛可探測車輛的停車位置，分別用不同的樣本數量進行計算，本文分別采取100，200，300，400，500，600組數據來對比效果，如圖6所示。

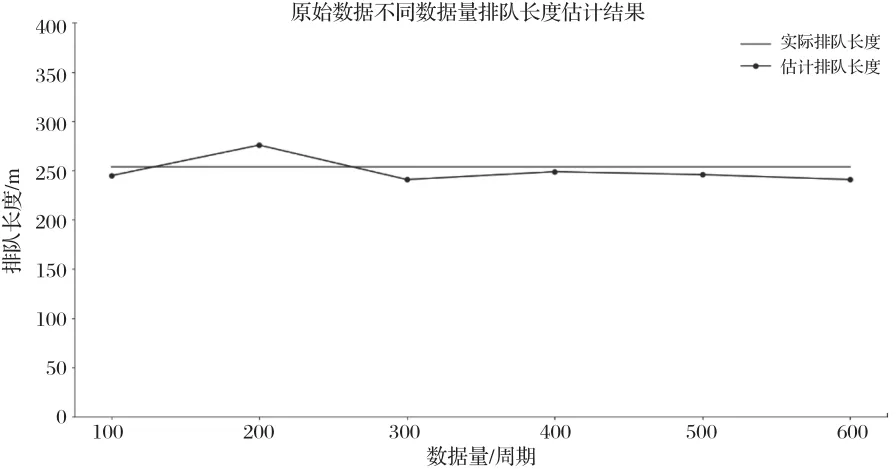
圖6 不同數據量下的排隊長度估計結果

分析數據可知，六組數據量的平均排隊長度準確率為94.9%，為了驗證文中方法的一般性，故將得到的1 200個軌跡數據隨機排列，在利用上述方法計算排隊長度，得到的結果如圖7所示。

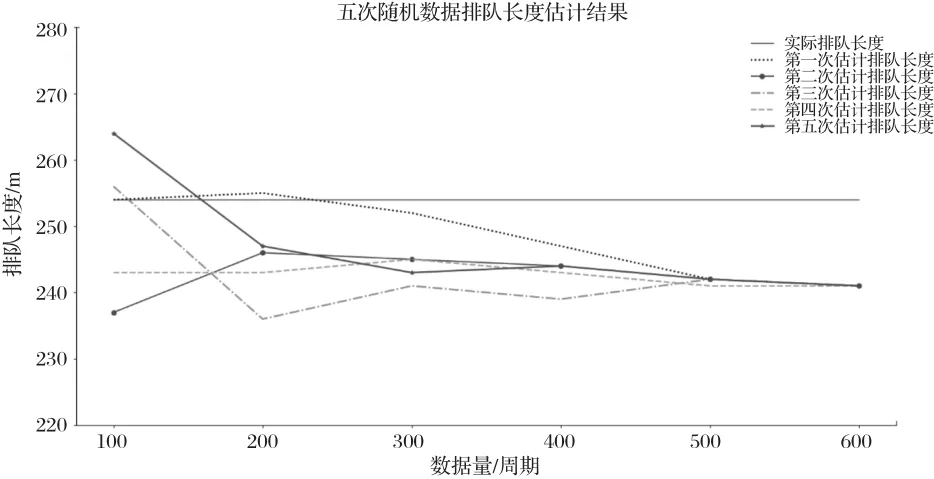
圖7 隨機數據在不同數據量下的排隊長度估計結果

由圖7數據可知，五次隨機數據的平均排隊長度為245 m，準確率為96.5%，準確率最低的一次為92.9%，故驗證方法有效，可以較為準確的估計交叉口處的排隊長度。

5 結語

本文提出了一種更通用的基于軌跡數據的排隊長度的估算方法，對于每個特定的運動和每個特定的時間段，通過對可探測車輛的歷史軌跡數據進行匯總，只要已知交叉口處第一輛可探測車和最后一輛可探測車的停車位置，估算得到的排隊長度準確率可以達到90%以上。與李愛杰等[7]基于交通波理論的現有研究不同，本文的方法不假定車輛的到達過程或排隊過程的類型。因此，該方法既適用于欠飽和情況，也適用于過飽和情況。