基于離散數據的雙螺桿壓縮機共軛轉子型線計算

盧家倫，田雅芬，邢子文

（西安交通大學，陜西西安710049）

1 引言

雙螺桿壓縮機由于具有結構簡單、工作可靠、效率高、操作簡單等一系列的優點，被廣泛應用于空氣動力、制冷以及石油化工等工業領域，在壓縮機市場中占據著十分重要的地位。螺桿壓縮機中，最關鍵的是放置于機殼內的一對相互嚙合的轉子。轉子型線是螺桿壓縮機設計中的核心技術，因為轉子型線的好壞基本決定了螺桿壓縮機泄漏特性以及動力特性的優劣。轉子型線設計是開發高性能雙螺桿壓縮機的關鍵技術之一，螺桿壓縮機性能的不斷提高以及市場份額的不斷擴大，是與轉子型線的發展密不可分的。國際上著名的螺桿壓縮機生產廠家，都是伴隨著新型線的開發成功而不斷發展壯大的。目前螺桿壓縮機型線設計主要使用解析法，但使用解析法比較復雜。按傳統的解析法，用一次或二次曲線來構成型線有其局限性，它不可能采用無限多段曲線向轉子型線的最優法逼近。而應用數值法計算，可按人們的愿望任意修正型線，使型線設計靈活多樣，有利于加速型線的更新換代。

邢子文[1]總結了螺桿壓縮機轉子型線設計和計算方法；N.Stosic[2]將齒輪與齒條的嚙合原理應用于螺桿壓縮機的端面型線研究中；Dmytro Zaytsev[3]則利用嚙合線與端面型線間的關系，依據嚙合線來生成端面型線；劉揚娟[4]通過三次樣條曲線擬合的方法計算型線一階導數，實現共軛型線的數值計算；段輝超[5]、穆安樂[6]則是通過三次參數樣條擬合的方法求出一階導數再求解型線的共軛型線；馬仙龍[7]、羅澤剛[8]等采用了NURBUS（非均勻有理B樣條）曲面的形式表示轉子型線的方法。

根據參數樣條擬合計算一階導數的方法，對于目前由多段二次曲線連接而成的轉子型線的計算存在“奇異點”的問題。本文描述了使用參數樣條擬合求解一階導數并進一步求解共軛型線的方法和步驟，提出了對奇異點的解決辦法，最后通過計算型線和理論型線的法向間隙誤差的方法衡量計算方法的優劣。

2 計算共軛型線

為了用數學方程描述螺桿轉子型線中各段組成齒曲線，建立如圖1所示的4個坐標系：

（1） 固結在陽轉子的動坐標系O1x1y1；

（2） 固結在陰轉子的動坐標系O2x2y2；

（3） 陽轉子的靜坐標系O1X1Y1；

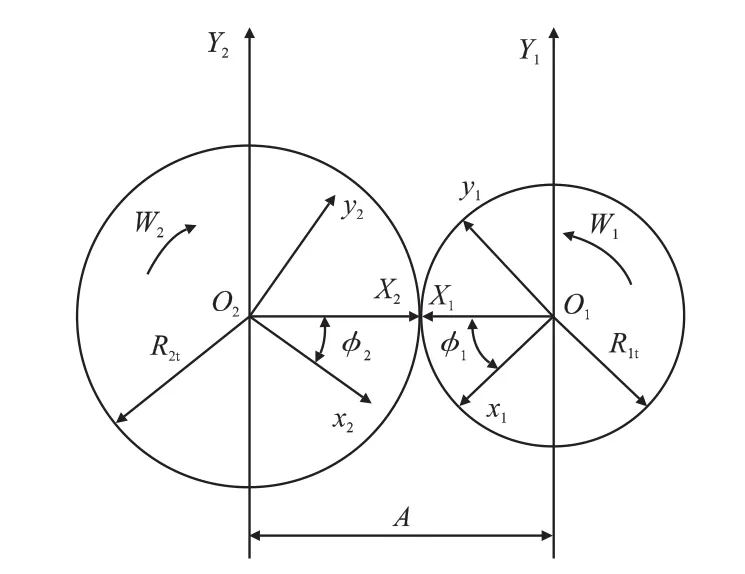
圖1 坐標系關系圖

（4） 陰轉子的靜坐標系O2X2Y2。

由于螺桿壓縮機的陰、陽轉子之間是定傳動比嚙合，故有

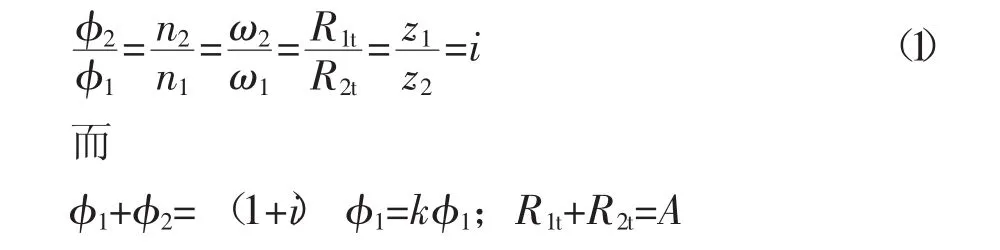
式中 φ2、φ1——陰、陽轉子轉角

n2、n1——陰、陽轉子轉速

ω2、ω1——陰、陽轉子轉速

R2t、R1t——陰、陽轉子節圓半徑

z2、z1——陰、陽轉子齒數

i——傳動比

A——陰、陽轉子中心距

螺桿壓縮機轉子型線上的每一點，都可表示在上述4個坐標系中，各個坐標系之間可以相互變換，這里只需要用到固結在陰、陽轉子上的動坐標系之間的變換。固結在陰、陽轉子上的動坐標系的變換關系如下

（1） 動坐標系O1x1y1與動坐標系O2x2y2的變換

對于組成齒曲線為參數方程的轉子型線，其包絡條件通式為

由于陰轉子的端面型線是以離散點的形式給出，各點的坐標為（x2j，y2j）（j=1，2，3……n），對于上述的包絡條件式（3）并不適用，為此對包絡條件通式推導可得

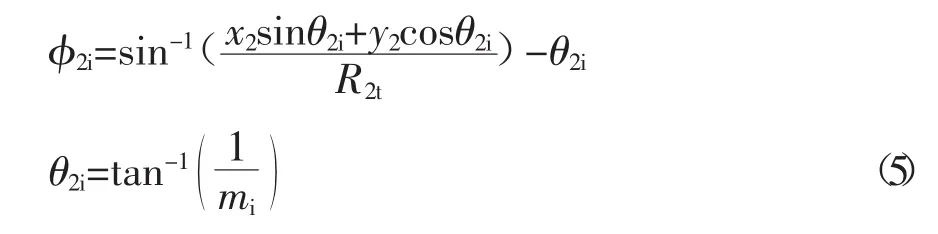
式中mi——一階導數值

聯立（2）、（5） 兩式即可求得與陰轉子端面型線共軛的陽轉子端面型線，其中離散點的一階導數值通過三次樣條函數或者三次參數樣條函數擬合求解獲得。

3 計算一階導數

在解決工程實際問題中，工程技術人員常常會將一些指定的樣點連結成一條光滑的曲線，這樣的曲線稱之為樣條曲線，對其進行數學模擬導出的函數叫做樣條函數。對于一般的曲線，用三次樣條函數可以很好的求出各離散點的一階導數，但是它存在一定的局限性[9]：

（1） 大撓度問題。在大撓度的情況下，三次樣條擬合精度不高，光順性變差，甚至不能使用，而螺桿壓縮機的轉子型線十分復雜，往往存在大撓度問題。

（2） 缺乏幾何不變性。也就是說，在給定了型值點的位置和邊界切向后，用三次樣條函數表示的插值曲線，依賴于坐標系的選擇，樣條曲線隨著坐標系的改變而改變。這既是它的優點又是它的缺點：優點在于可以適當的旋轉坐標系，把大撓度適當的轉化為小撓度，避免出現光順性變差甚至變壞的問題；缺點在于有可能找不到這樣的一個坐標系化大撓度為小撓度，并且需要多次試驗來找到這樣的一個坐標系，比較麻煩。而采用三次參數樣條曲線則可以避免這樣的問題。

三次參數樣條曲線：

現在設定在直角坐標平面上給定n個型值點Pi（xi，yi），i=1，2，…，n。那么相鄰兩型值點的弦長為設定參數曲線P→（t）=（x（t），y（t）），那么第i段曲線的方程為

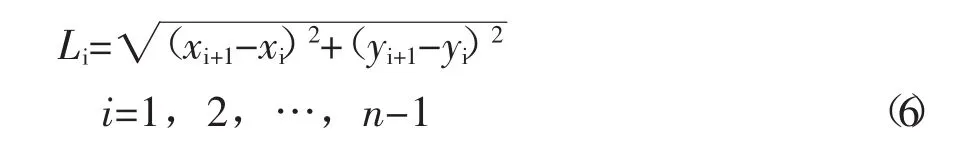
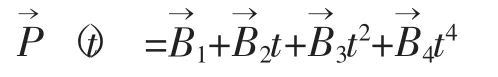
由于相鄰兩段曲線在型值點Pi處一階和二階導向量連續，經過推導以及化簡后得到以下方程

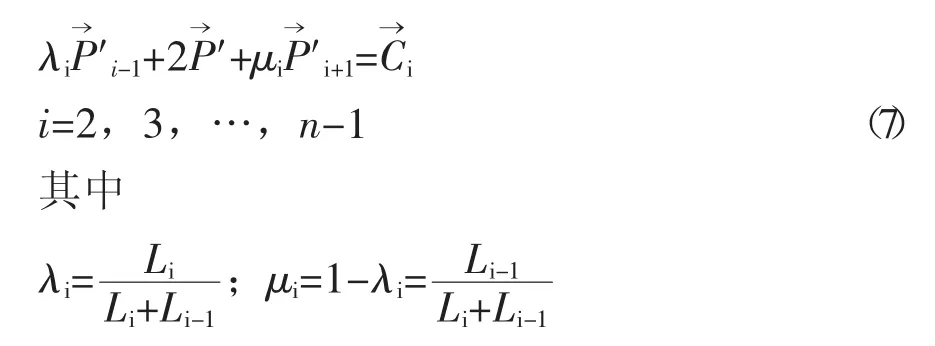
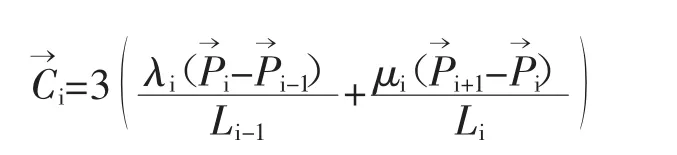
以上共有n-2個線性方程，為求解n個需要的導數值，還需要補充2個邊界條件。邊界條件即是整個曲線在2個端點處應適應的條件，通常應根據實際問題的需要來確定。對于螺桿壓縮機轉子型線，采用夾持端邊界條件即可，這時要求

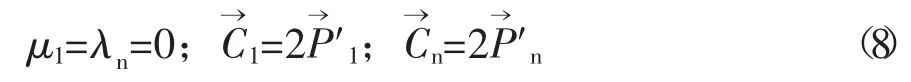
將n-2個連續方程（7） 以及2個邊界條件（8）寫成矩陣形式，則有

由此，解以上矩陣，即可求得各型值點處的一階導數。

4 實例計算

對于以離散點形式給出的型線數據，采用參數樣條擬合，能夠精確地通過每個型值點，可以很好地進行擬合。但是轉子型線一般由多段二次曲線連結在一起，在二次曲線連接處可能出現兩段曲線在該處的二階導數不相等的情況，不符合參數樣條函數擬合條件，從而導致一階導數以及共軛型線的計算存在一定的誤差。

表1列出部分型線數據，并用參數樣條函數求出陰轉子各型值點的一階導數mi值，對應的轉子型線見圖2。

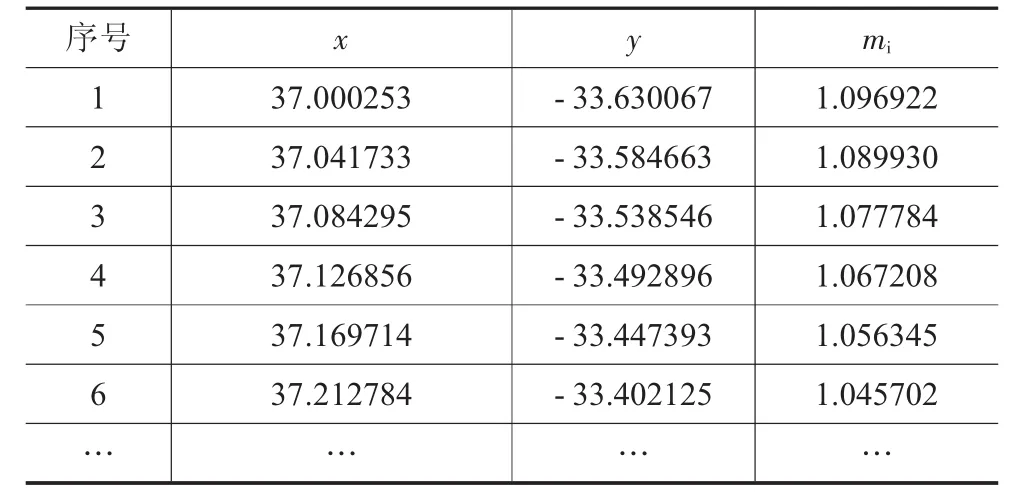
表1 曲線1相關型線數據

程序運行計算得到的共軛型線結果如圖3，運行結果與解析法計算得到的對應理論型線型值點的距離誤差圖如圖4所示。

可以發現，計算得到的共軛型線與給出的理論型線基本重合，但在一處地方出現了2個奇異點。

對于出現的這2個奇異點，目前查找到的文獻中沒有提到這樣的一個情況。在認為型線本身以及共軛型線計算方法沒有問題的情況下，認為一階導數的計算存在誤差，而造成這樣的誤差的原因如下：三次參數樣條曲線擬合的前提條件是相鄰兩段曲線在型值點處的一階導數和二階導數連續，而出現奇異點處對應的陰轉子型線處是兩段型線的連接處，理論型線中，該連接處的要求是函數連續以及一階導數連續，并沒有要求二階導數連續，那么在該連接處不符合三次參數樣條曲線擬合的前提條件。因此在該連接處附近用三次樣條函數擬合計算一階導數存在誤差。

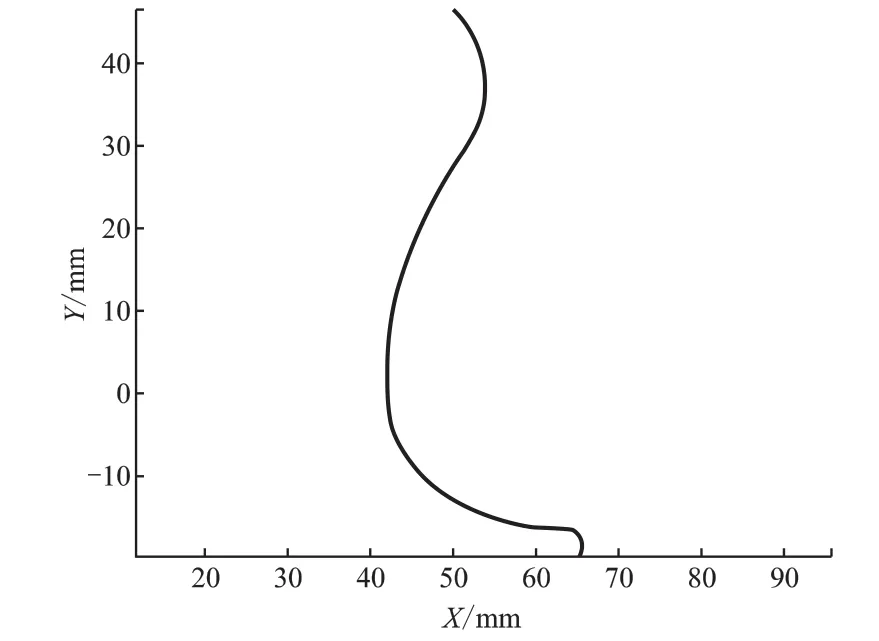
圖2 陰轉子型線

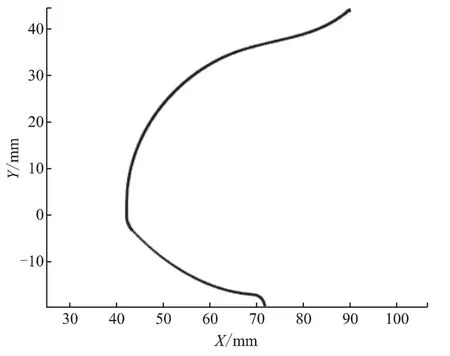
圖3 對應的共軛陽轉子型線

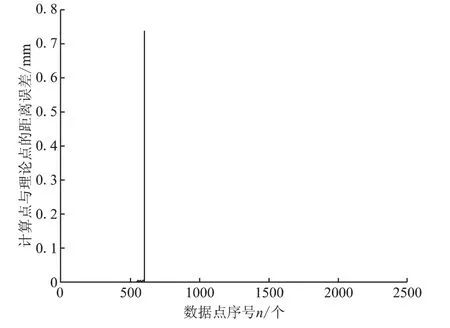
圖4 共軛型線距離誤差分布

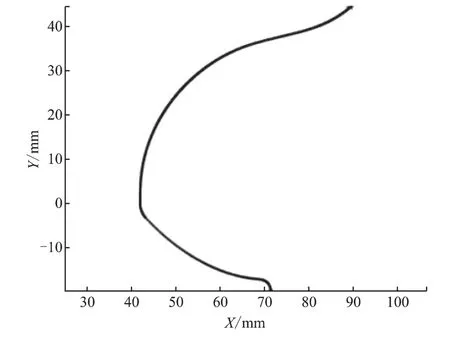
圖5 修正后曲線1對應的共軛陽轉子型線

為了解決這個問題，采用以下方法重新計算一階導數：對出現奇異點處的這兩個點的一階導數進行修正，以誤差較大的奇異點對應點為端點，把陰轉子型線拆分為兩段型線重新計算一階導數，并把重新計算的奇異點對應的一階導數替換之前的一階導數。重現計算后的共軛型線曲線圖如圖5，距離誤差分布圖如圖6所示。

可以看到，對陰轉子曲線連接處的一階導數進行修正之后，奇異點消失，計算得到的共軛陽轉子型線與理論共軛陽轉子型線幾乎完全重合在一起，計算點與理論點的最大距離誤差大大減少，其中曲線1的最大距離誤差由0.74 mm降低至0.034 mm。此時，雖然計算點與理論點距離上存在著偏差，但計算點依然是在型線上的，而不是完全偏離型線，所以通過計算對應的計算點和理論點的距離的方法來衡量誤差的方法并不準確。最為準確的方法應當是計算理論型線和計算型線之間的法向間隙來衡量計算偏差。由于陰轉子型線型值點較多，兩型值點之間的距離較小，因此在計算型線法向間隙時可以假設兩型值點之間的型線為直線。那么每一型值點處的法向間隙誤差就是計算點和與其最近理論點的距離的法向分量，其中法向方向是指計算點在計算型線的法線方向，根據該計算點的一階導數（切向方向） 求得。計算得到的型線數據與理論型線近似法向間隙值如圖7所示。

可以看到，對于給出的陰轉子型線，其共軛型線的計算型線與理論型線最大的法向間隙誤差為0.00022 mm。

為了衡量法向間隙誤差總體誤差的大小和偏差，可以采用均值與方差或者標準差進行描述，其具體的計算式如下

均值

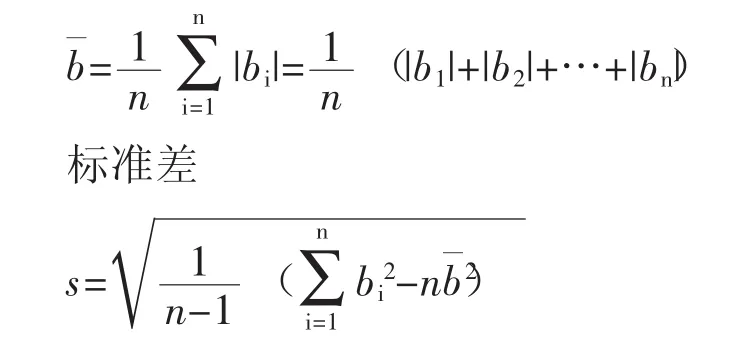
對于給出的陰轉子型線，其共軛型線法向間隙誤差分布的均值為：bˉ=4.59e-7mm，標準差為s=4.81e-6mm。

綜上可得相關結果的誤差很小，小到目前測量方法都識別不出來的程度，完全滿足實際工業生產的需要，因此認為程序計算的結果是十分正確可靠的。

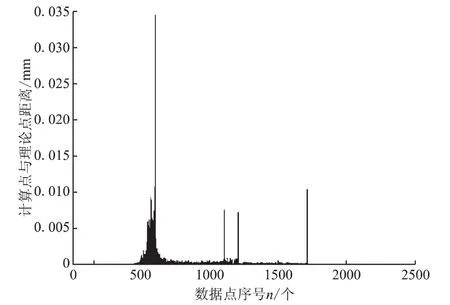
圖6 修正后共軛型線的距離誤差分布

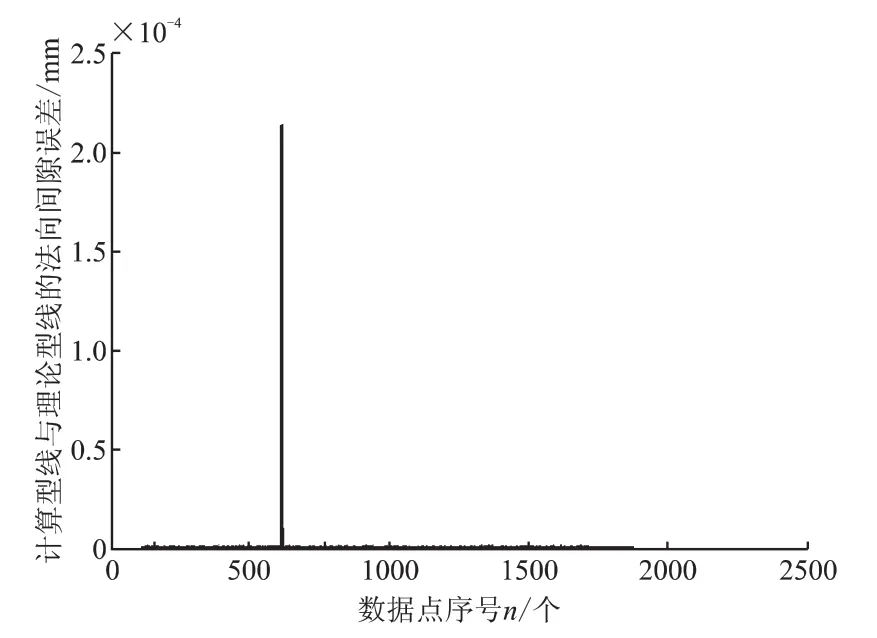
圖7 計算型線與理論型線的法向間隙誤差

5 結論

本文通過相關實例給出了根據任意螺桿壓縮機陰轉子型線計算，其共軛陽轉子型線的一般原理和具體操作方法，并通過把計算結果與理論型線數據做對比，分析和評估了這種型線計算方法的誤差，說明了該方案的精度和可行性，對相關的工業生產具有很強的指導性。此外，作者發現在利用三次參數樣條函數計算一階導數具有幾何不變性的優點，但是對于陰轉子型線連接處的一階導數計算存在一定的誤差，需要對一階導數進行一定的修正。此外，對于計算型線與理論型線的誤差時，應當采用法向間隙誤差衡量，而不是簡單地采用計算型線與理論型線距離誤差來衡量，希望對今后相關設計人員的計算能起到一定的啟發作用。