擠壓筒內筒磨損有限元分析

羅遠新，徐俊峰，王勇勤，張 君

(1. 重慶大學機械工程學院，重慶400044;2. 中國重型機械研究院股份公司，陜西 西安 710032;3. 金屬擠壓與鍛造國家重點實驗室，陜西 西安 710032)

0 前言

坯料與內筒接觸面上壓強高，工作環境溫度高，潤滑劑容易被擠出接觸面[1,2]。在這些惡劣條件下，擠壓筒在使用一定周期之后，擠壓出的型材會出現劃傷、氣泡、起皮、成層等缺陷，將擠壓筒內筒用堿性溶液清洗后發現，內壁特別是出料口端的磨損十分嚴重[3]。擠壓筒磨損不僅會造成產品質量問題，磨損點會成為擠壓筒疲勞開裂的開裂點，擠壓筒損壞會給企業造成巨大的經濟損失和安全隱患。因此，研究擠壓筒的磨損為實際生產提供參考具有十分重要的意義。

擠壓筒內筒磨損通常為粘著磨損[4]，Archard模型[5]是分析粘著磨損最常用的模型，近些年來，不斷有學者通過修正Archard模型進行磨損研究，Behrens[6]從優化模具壽命的角度出發將準確預測模具的磨損壽命作為一個重要要求，基于現場測試的試驗數據，考察其硬度隨熱軟化的演化情況，提出了一個修正的Archard模型，使得該模型的預測精度與應用范圍均有所提高。Lee等[7]通過試驗考察了溫度對摩擦因子的影響以及磨損因子隨溫度的變化規律，并據此對Archard模型進行了修正，最后采用仿真模擬研究了溫擠壓過程中模具的磨損壽命。Kang等[8,9]針對普遍采用的預測金屬成形制造中工模具磨損的Archard模型進行了修正，將模型中的工模具硬度由常數變為與溫度和操作時間有關的函數，采用仿真模擬分析手段研究了等溫擠壓過程中工模具的磨損情況；將修正后的Archard模型與仿真模擬相結合，成為研究磨損常用手段之一。王雷剛等[10]在修正的Archard磨損模型基礎上，采用有限元分析軟件對兩種形狀的擠壓模具型腔進行磨損分析。

為了方便計算，本文建立了某型號擠壓筒模型的二維有限模型，以內筒內壁的徑向位移量作為磨損量。將改進型Archard磨損模型通過FORTRAN語言編寫入用戶自定義的自適應網格(ALE)約束條件子程序UMESHMOTION中，利用有限元軟件ABAQUS模擬擠壓筒的磨損。對擠壓筒工作過程中內筒的磨損進行仿真模擬，探究坯料屈服強度、摩擦系數和H13屈服強度對磨損性能的影響規律。

1 基于修正Archard模型的擠壓筒磨損深度計算公式

(1)

式中，Q為磨損體積；W為坯料與擠壓筒內筒接觸面的法向壓力；v為坯料與擠壓筒內筒之間的切向相對滑移速度，σs內筒材料的屈服強度，K為磨損因子。

擠壓筒內壁上的作用力主要來自坯料，取擠壓筒內壁表面的一個微元為研究對象，設其承受的正向壓力為P，承載面積為△A，則內壁承受的法線載荷為：W=P△A。因此，擠壓筒內壁的磨損率可以表達為

(2)

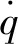
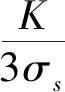
式(2)可表示為

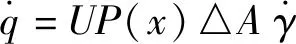
(3)

擠壓筒徑向受力基本一致，擠壓正應力在軸向位置變化分布，針對本課題采用的二維模型，某一軸向位置的磨損情況可以用徑向磨損深度來代替整體磨損體積，微元在無窮小的時間dt磨損厚度增量為dh，dV=△A·dh，代入到(3)得：

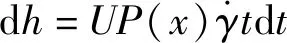
(4)

有限元模擬時，采用離散化計算方法進行求解，將磨損深度h進行離散化計算，選取有限小的時間段△t為時間增量，同時認定U和P在△t內為恒定值，該時間段內的磨損深度△h可通過公式(5)求出。

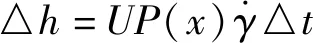
(5)

單次擠壓時間分割成m個時間間隔，第i節點單次擠壓磨損深度△h為

(6)

第i節點n次磨損總深度h為

(7)

2 擠壓筒磨損的有限元模擬

本文主要研究擠壓筒工作過程中內筒的摩擦磨損行為，因此試驗材料為熱作模具鋼H13以及代表性的鋁坯料航空鋁材7050。在500 ℃高溫下，對H13熱作模具鋼進行單軸拉伸試驗獲得熱彈性模量和屈服強度，磨損因子[11]。

2.1 擠壓筒的有限元模型

在有限元軟件ABAQUS中，模擬7050鋁合金棒材成型過程，擠壓比為3∶1，溫度為500 ℃。擠壓筒的有限元模型如圖1所示，各筒之間由于過盈配合裝配，摩擦系數設為0.8，對擠壓筒和模具進行軸向約束，坯料沿軸向勻速向下擠出。擠壓筒和坯料都是軸對稱圓柱體，磨損量的大小以內筒徑向尺寸減少量表示，所以為了計算方便采用二維模型。將修正后的Archard磨損模型通過FORTRAN語言編寫入用戶自定義的自適應網格(ALE)約束條件子程序UMESHMOTION中，ALE自適應網格約束區域如圖2所示。

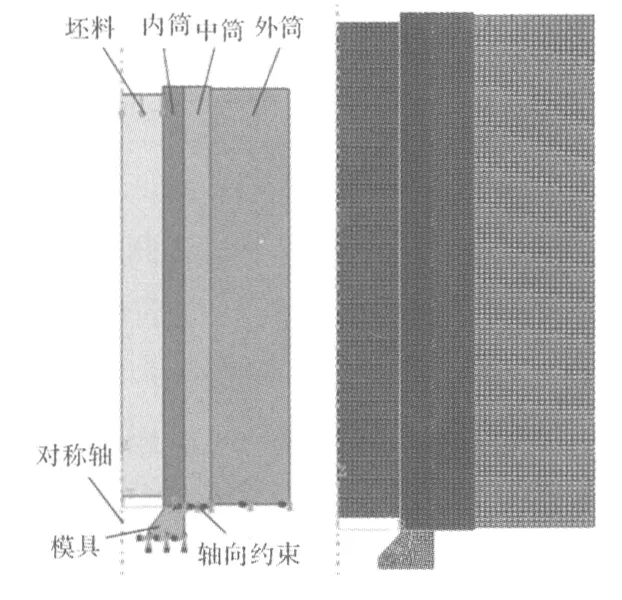
圖1 擠壓筒的有限元模型

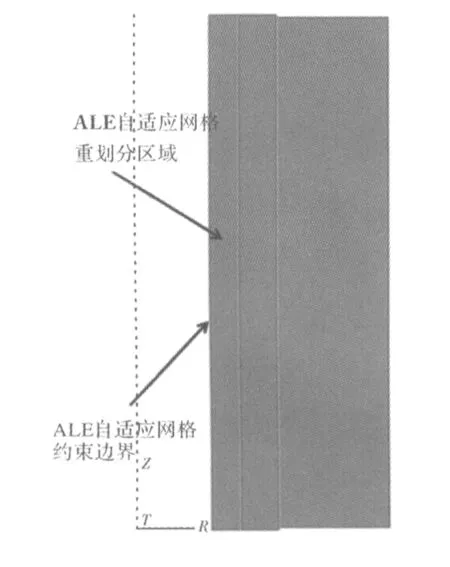
圖2 ALE自適應網格劃分區域

2.2 磨損模擬結果與分析

根據文獻[12]可知，擠壓筒在經過15 600次擠壓循環后會發生蠕變疲勞失效，因此在進行擠壓筒磨損計算時循環次數設為15 600次。圖3為磨損模擬結果，其擠壓速度為v=0.1 m/s，從圖3中可以看出擠壓筒內壁靠近出料口的徑向位移大幅增加，即由于多次擠壓，擠壓筒出料端的內壁表面已經出現明顯的磨損，內徑明顯變大。在擠壓過程中，擠壓筒內筒承受軸向摩擦力，造成內筒內表面產生磨損。由圖3b可以看出，雖然整個擠壓筒的軸向位移相對于徑向位移來說很小，但可以看出擠壓筒內筒靠近入料端部分的軸向位移較大，且與擠壓方向相反，并且在與中筒配合的面上分布更顯著。這是因為坯料被擠料桿沿著擠壓方向擠壓時，坯料對擠壓筒內筒的摩擦力是內筒向擠壓反方向運動，因此導致了內筒沿軸向向坯料后端運動。如圖4所示，將過盈裝配后與多次擠壓循環后的徑向位移方分布進行對比，其差值即為其磨損量。可以看出擠壓筒內壁出料端的磨損情況最嚴重，因為該處與坯料的接觸時間最長，并且磨損程度沿軸向從出料端往入料端逐漸減少。這與實際生產過程中觀察到的出料端磨損嚴重的現象一致。

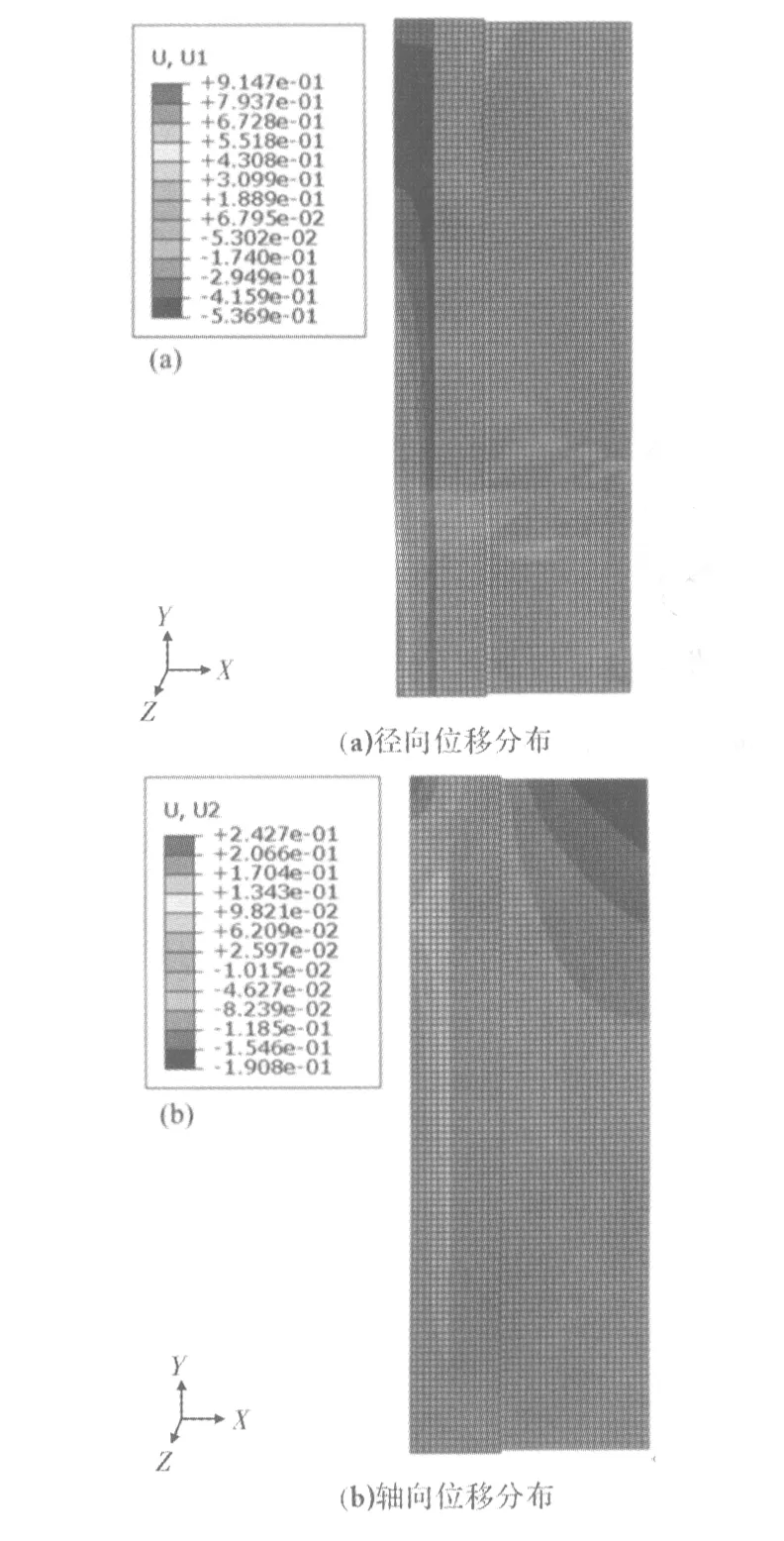
圖3 蠕變疲勞失效時即N=15 600次后位移分布

圖4 擠壓循環周期后擠壓筒內壁磨損分布

3 擠壓筒磨損影響因素分析

3.1 坯料屈服強度對擠壓筒磨損的影響

為了研究不同擠壓接觸力對擠壓筒內壁磨損情況的影響，本文模擬了擠壓筒內壁在三種不同擠壓坯料下的磨損情況，摩擦系數為0.25，材料屈服強度分別為30 MPa，60 MPa以及90 MPa，將其所產生的擠壓接觸力分別命名為Cpress1，Cpress2，Cpress3。圖5為不同擠壓坯料下擠壓筒內壁在擠壓循環10 000次后的磨損分布，可以看出擠壓筒內壁的磨損深度與擠壓坯料的屈服強度成正相關，這是因為坯料的屈服強度決定了使坯料發生塑性變形的擠壓力的大小，即決定了影響磨損量的接觸應力大小，因此影響了磨損情況。由此可知，擠壓力越大，擠壓筒內筒內壁的磨損越嚴重，越容易過早引起擠壓生產的不正常運行。由于正常磨損失效不可避免，因此可根據模擬計算情況，對實際擠壓參數進行調整，以期延長磨損壽命。

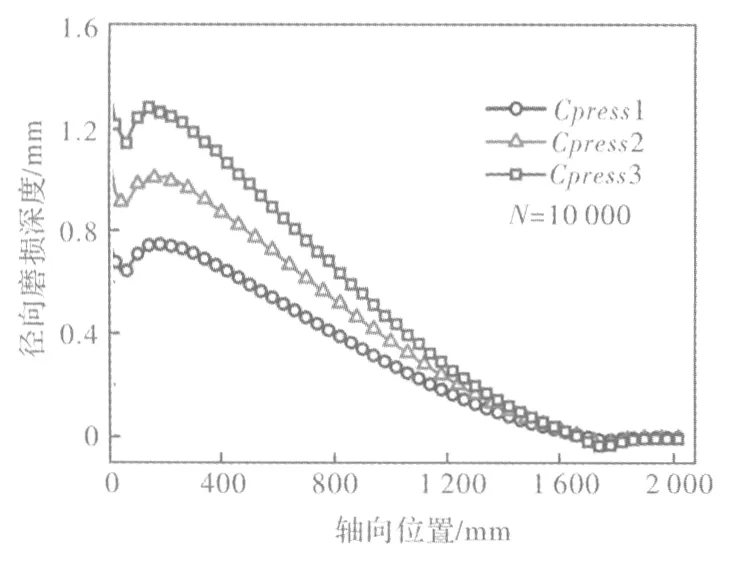
圖5 N=10 000次循環擠壓后不同材料擠壓坯料下擠壓筒內壁磨損沿軸向的分布

為了研究不同摩擦系數對擠壓筒內壁磨損的影響，本文模擬在坯料屈服強度為90 MPa，在不同摩擦系數μ下循環10 000次，圖6是在不同的摩擦系數時，經過10 000次循環擠壓后不同摩擦系數下擠壓筒內壁磨損沿軸向的分布。從圖中可以看出，隨著摩擦系數的增大，磨損量也隨之增大。由Archard模型可知，磨損量只與接觸壓力和滑移距離有關，摩擦系數改變，間接的影響擠壓過程中坯料與擠壓筒內筒的接觸壓力，接觸壓力隨摩擦系數的增大而增大。摩擦系數主要影響接觸面的剪切力，當剪切力較大的時候，材料容易發生疲勞磨損，因此在生產中要盡量避免接觸面之間產生較大的摩擦力。

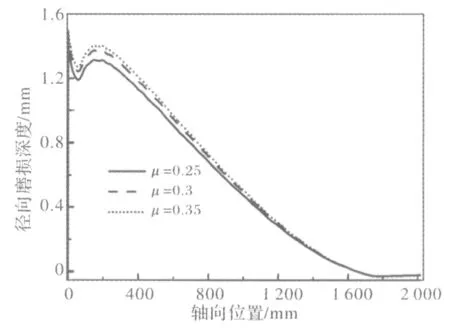
圖6 N=10000次循環擠壓后不同摩擦系數下擠壓筒內壁磨損沿軸向的分布

由Archard模型可知，H13坯料強度也是影響擠壓筒磨損性能的重要因素，為了研究坯料強度對擠壓筒磨損性能的影響，模擬在坯料強度為90 MPa，摩擦系數為μ=0.25，H13屈服強度分別為σs=898.98、σs=998.98、σs=1098.98，經過10 000次循環之后，擠壓筒不同位置的磨損分布如圖7所示。由圖7可知，各部位的磨損量和H13屈服強度成負相關關系，屈服強度越高，擠壓筒的磨損量越小。

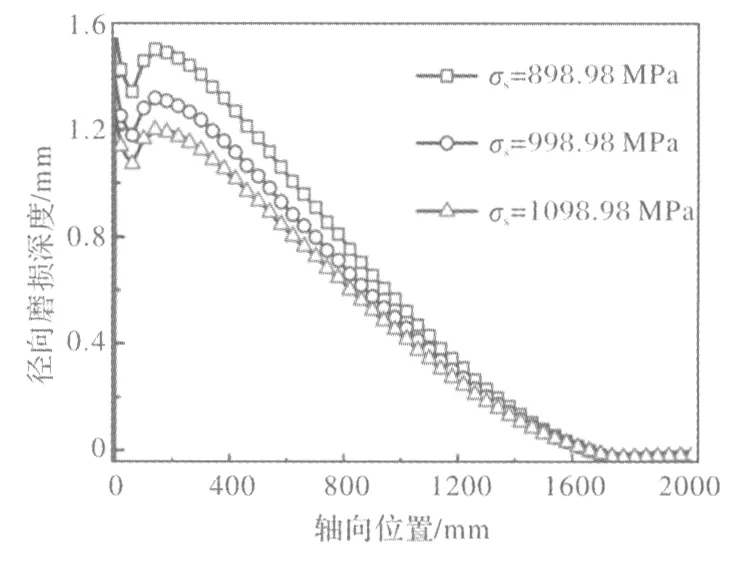
圖7 N=10 000次循環擠壓后不同摩擦系數下擠壓筒內壁磨損沿軸向的分布

4 結論

(1)擠壓筒內筒出料端的磨損情況最嚴重，因為該處與坯料的接觸時間最長，并且磨損程度沿軸向從出料端往入料端逐漸減少。

(2)坯料屈服強度和摩擦系數對磨損的影響是正相關的，擠壓筒材料的屈服強度與對磨損的影響成負相關關系。