對九腳探頭磁導率、檢測電壓與應力相關性研究
魏 明,馬占國,殷春浩,徐振坤
(1.中國礦業大學 a.深部巖土國家重點實驗室;b.物理學院, 江蘇 徐州 221116; 2. 徐州工程學院 數學與物理科學學院,江蘇 徐州 221018 )
鐵磁部件受到動靜載荷的作用會產生應力集中,引起部件的局部疲勞、失效,如何快速有效地測量鐵磁部件的應力分布,對鍋爐、壓力容器、起重機械等大型設備具有十分重要的意義[1-2]. 在應力作用下,鐵磁部件被磁化時具有磁各向異性的特點,利用磁性探頭的檢測信號大小來反映磁各向異性強弱,從而判斷鐵磁部件的應力大小. 因此作為磁各向異性測量系統最重要部分的磁性探頭,受到人們越來越多的關注,如何獲得磁化強度大、穩定性強、功耗低的探頭,成為目前研究的熱點之一[3].
在磁測探頭的研制和應用這一領域,R. Langman[4-5]在Π型兩腳磁測探頭的基礎上,設計了可旋轉的測量裝置用于磁場檢測,H. Yamada[6]等研究了四腳磁測探頭磁路,K. Kashiwaya[7]等改進了四腳磁測探頭,T. Isono[8]等在四腳探頭的基礎上,研制出了九腳探頭的磁測傳感器用于測量磁場強度. 石延平等設計了五腳[9]和六腳[10]差動式磁測探頭,并與應變電測試驗進行了比較. 趙洲等通過ANSYS模擬了九腳探頭,得到了探頭線圈距被測體不同距離的模擬圖[11],并對九腳探頭與二腳探頭的實驗結果做了比較,結果發現橫向應力與縱向應力的測定結果相似,且分布趨勢與焊縫處應力分布的理論定性分析基本吻合,初步驗證九腳探頭的測法理論分析的正確性[11]. 殷春浩、劉海順等利用四腳探頭和載荷實驗機標定了應力感度曲線[12-13],研究了磁性探頭測量間隙、探頭阻抗與靈敏系數的關系,根據九腳探頭不需要旋轉的獨特特點,提出磁輸出信號與應力間的力學模型,建立了微觀的磁通與宏觀的電信號的關系[14-15].
1 九腳探頭的檢測電壓與磁導率關系推導
T.Isono和S.Abukn等研制出九腳探頭,其結構如圖1所示,中間為勵磁探腳,圓周8個探腳為感應探腳,l1為沿探腳方向的磁路長度,l2為感應探腳與勵磁探腳間的磁路長度,S1為感應探腳橫截面積,S2為中心勵磁探腳的橫截面積, 8個感應探腳同時與中間勵磁探腳和被測材料形成閉合的磁路. 與傳統探頭相比,九腳探頭與試件接觸面積小[16],且測量應力比較小時探頭無需轉動即可測出該點的主應力差與主應力方向角,具有測試靈敏度高、測試系統簡單等特點.
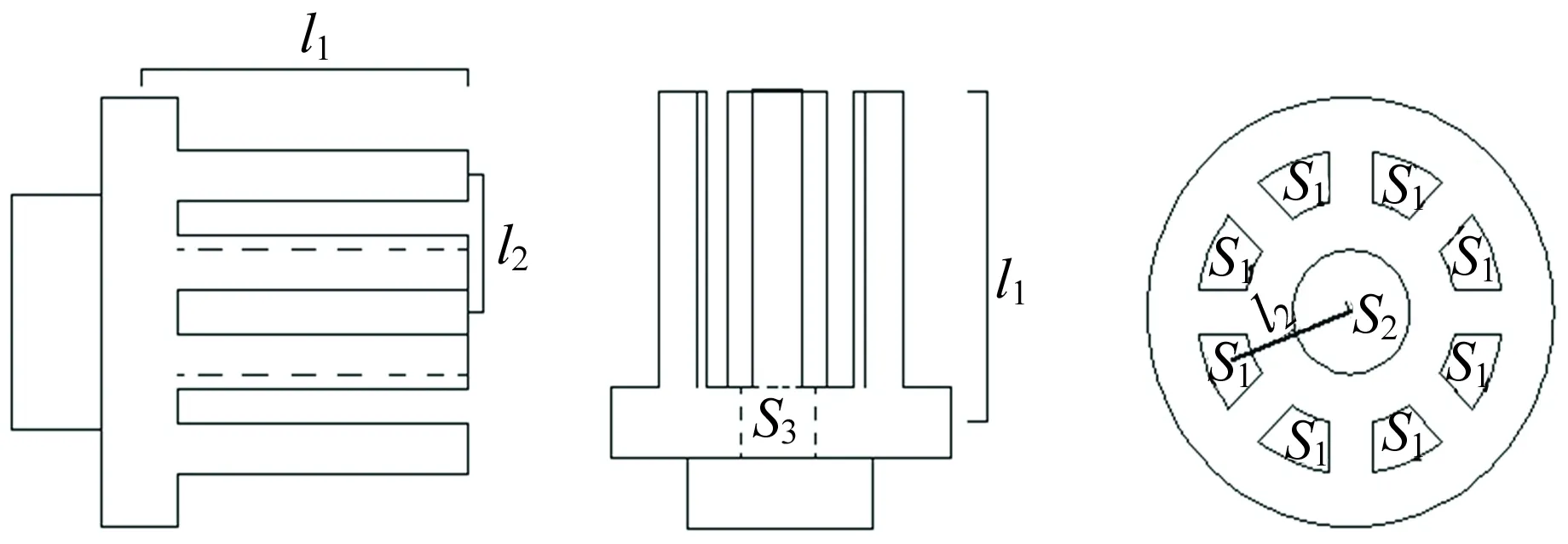
(a)側視圖 (b)俯視圖圖1 九腳探頭的結構示意圖
為了提高磁化強度和對樣品磁化的均勻性,以四周8個探腳作為勵磁探腳,中間探腳作為感應探腳. 當在勵磁探腳上加載交流電流時,勵磁線圈上產生交變的磁場和相應的磁動勢Fm,在此作用下,勵磁磁芯中會產生交變的磁通量Φm,Φm在探頭和被測對象之間形成閉合磁回路,由磁路理論和基爾霍夫磁路定律可知
Fm=n1i,
(1)
磁阻為
(2)
式中,n1是勵磁線圈的匝數,i是勵磁線圈電流,l是對應的磁路長度.
在閉合的磁路中,磁動勢Fm等于各部分磁壓降(Hili)之和,即
(3)
又因為
(4)
把式(4)和式(2)代入到式(3)可得
(5)
式中μi,Si和li分別對應磁路的磁導率、橫截面積和磁路長度.
因九腳探頭總共有8個勵磁探腳和1個感應探腳,每個勵磁探腳都和感應探腳構成閉合的磁路,則檢磁探腳的磁通量Φf可以表示為
(6)
根據法拉第電磁感應定律,檢測線圈的感應電動勢為
(7)
其中,n2為檢測線圈的匝數,假設勵磁電流i=Asin (ωt)(ω為角頻率,A為電流幅值),則式(7)可以改寫為
即便是習慣了網上買理財產品的客戶,社區服務點的近距離、咨詢式體驗和傳統的人際溝通同樣可以起到較好的購買體驗作用。
(8)
從而建立了檢測線圈的感應電壓ε(t)和磁導率μi的關系.
對于本實驗,閉合磁路是由鐵芯和被測材料2部分構成,因此,在對樣品進行測量前需要確定探頭的相對磁導率μr-t,然后再把探頭的磁導率μr-t作為已知量來計算被測樣品的相對磁導率μr-s.
實驗中將感應電壓ε(t)加載到RC積分放大器,則可以得到檢測電壓U同感應電壓ε(t)的關系為
(9)
測量工頻下的感應電壓有效值εeff和檢測電壓Ueff的數據并作圖,如圖2所示.

圖2 50 Hz條件下的感應電壓有效值εeff同檢測電壓有效值Ueff隨勵磁電壓峰值變化的曲線圖
通過擬合Ueff和εeff的關系曲線,得到
(10)
式中,α為對積分電路輸入與輸出數據的修正系數,α=1-0.000 64(Up-50),其中Up為勵磁電壓峰值.
(11)
其中
(12)
(13)
在式(13)中,探頭的相對磁導率μr-t是未知量,Ueff為測量量,α為電路修正系數,其余為九腳探頭的結構常量,因此可以計算出探頭的相對磁導率μr-t. 測量九腳探頭磁導率的示意圖如圖3所示.
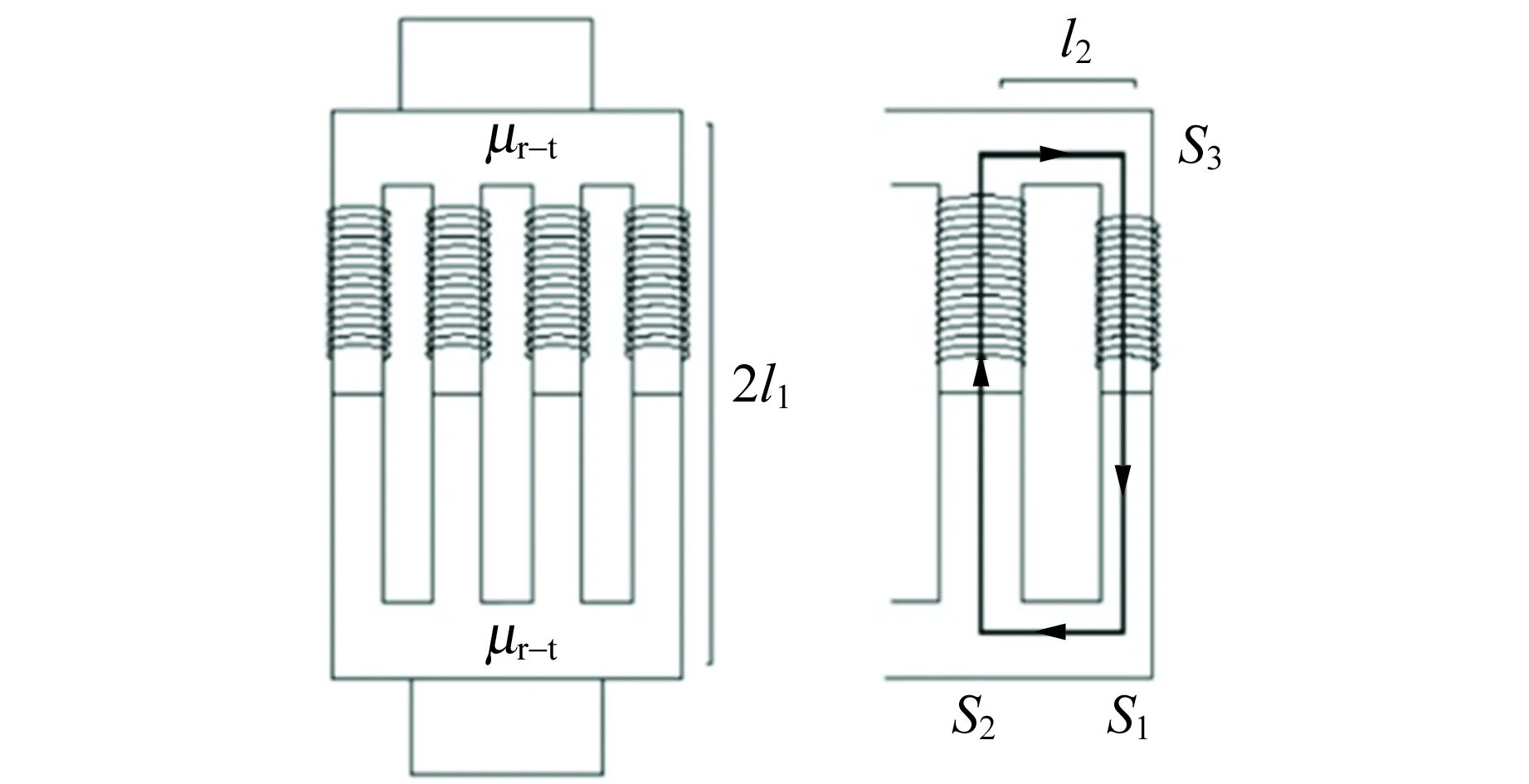
圖3 九腳探頭的磁導率測量示意圖
在樣品測試中,把被測的探頭換成被測樣品,圖4為測量時的示意圖,S4是被測材料部分的磁路橫截面積,則有
(14)
被測材料的磁導率μr-s、鐵芯相對磁導率μr和樣品檢測電壓Us-eff之間的關系為
(15)

圖4 樣品的磁導率測量示意圖
把探頭的磁導率μr-t代入到式(15),并結合九腳探頭和電路的參量可得到被測樣品的μr-s.
2 實驗結果與分析
實驗采用靜載拉伸的方式,對Q235,Q255,Q345#進行拉伸實驗,樣品尺寸按照GB/T 6397-1986的標準,按照50 MPa的步進方式進行實驗測試,并記錄了不同拉力下,磁導率的檢測電壓差值隨著勵磁電壓的變化曲線圖,如圖5所示.

(a)Q235
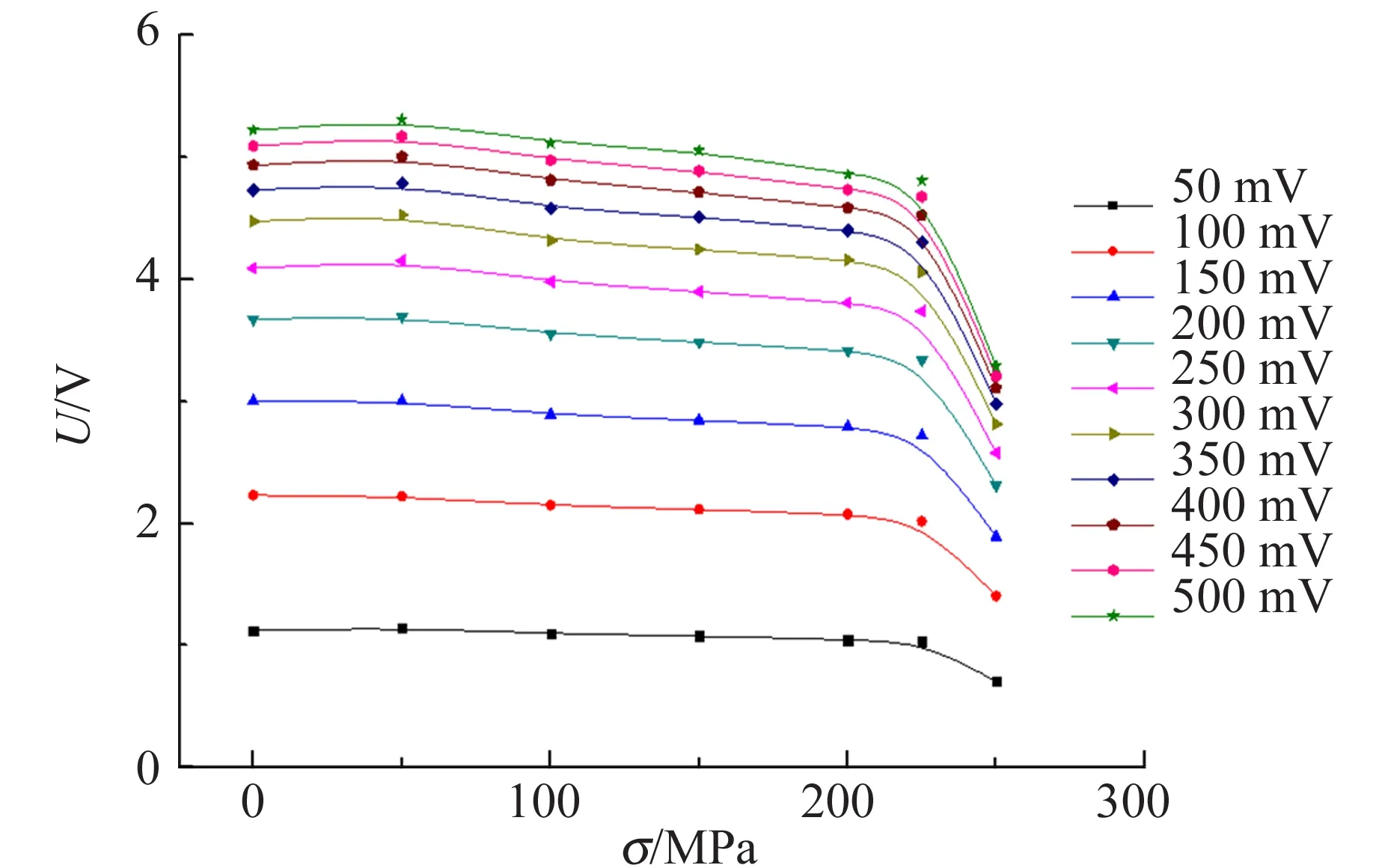
(b)Q255
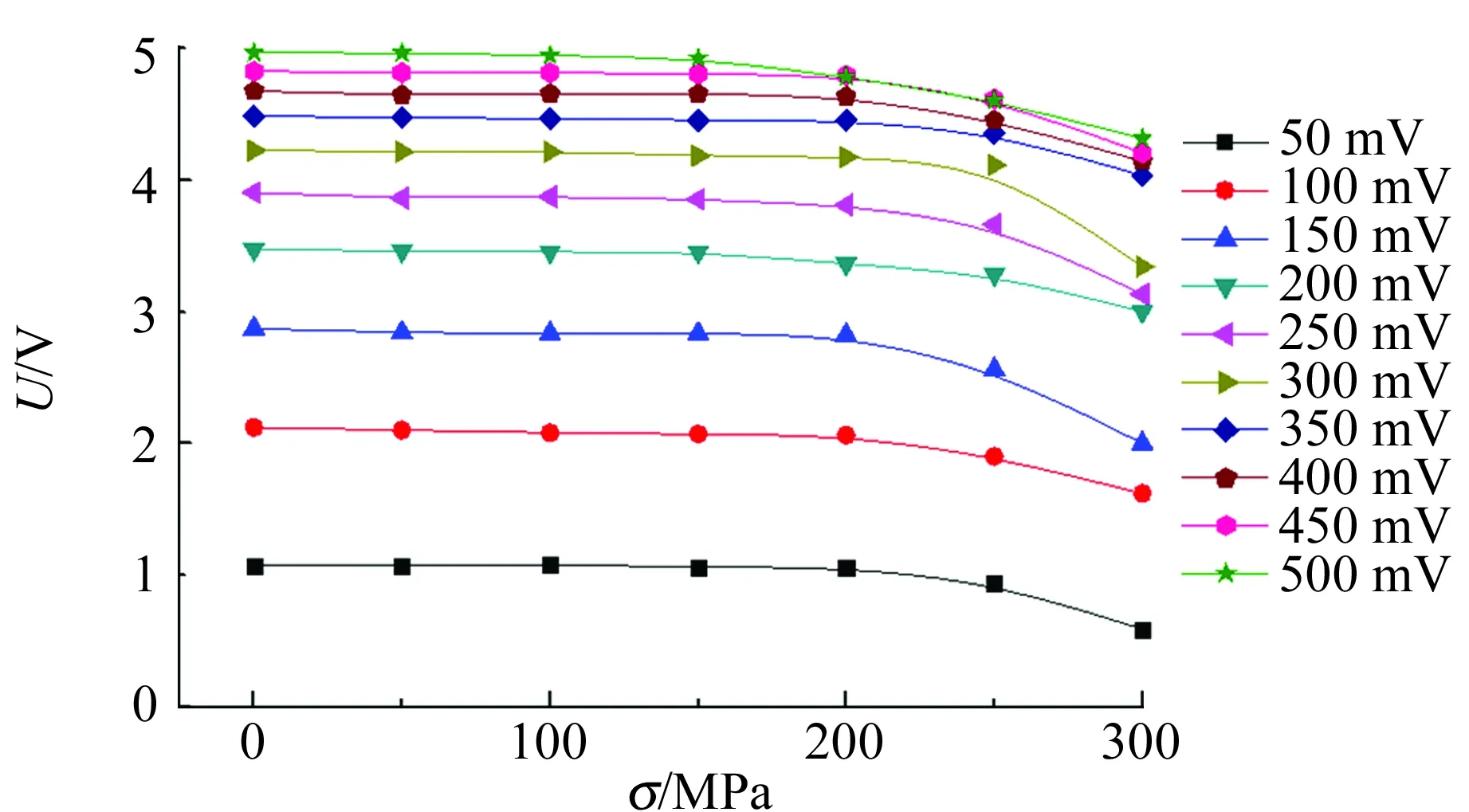
(c)Q345圖5 不同應力條件下,磁導率的檢測信號與0 kN應力條件下的差值隨勵磁電壓變化的關系曲線
從圖5中可以看出,在相同的應力條件下,隨著勵磁電壓的升高,探頭的檢測電壓也升高,但升高的幅度會隨著逐漸減小,在50~200 mV之間,檢測電壓幅值增加較大,勵磁電壓大于200 mV后,檢測電壓幅值增加越來越小,并趨于穩定. 從樣品磁化的角度分析,勵磁電壓的大小代表勵磁磁場的大小,勵磁電壓越大,磁場強度越大,在樣品未飽和磁化前,樣品的磁化強度會隨著勵磁磁場的增加而快速增加,當樣品磁化強度趨于飽和時,樣品的磁化強度隨著勵磁磁場的增加而緩慢增加.
在樣品在相同的勵磁電壓的條件,即相同的勵磁磁場下,九腳探頭的檢測電壓隨著應力的增加而呈現出減小的趨勢,Q235,Q235和Q345樣品的輸出電壓隨應力增加而減小的趨勢較為明顯,3個樣品的輸出電壓整體呈現出減小的趨勢,但中間過程存在小的波動. 從圖5中可以看到,在樣品沒有達到屈服之前,樣品的輸出電壓幾乎隨著應力的增加呈線性遞減,當樣品接近屈服狀態或者外應力超過屈服應力時,樣品的輸出電壓遞減較快,呈現非線性變化的特點.
分析其原因如下:當樣品未受力和未被磁化前,樣品對外不顯磁性,當樣品在應力和局部磁化的作用下,樣品內部的磁疇沿著外磁場方向偏轉,磁疇取向的變化導致樣品磁化方向的變化,導致檢測線圈的磁通量的變化產生感應電壓,在初始磁化時,樣品內部磁疇的取向由隨機取向逐漸轉變為沿外磁場方向,導致樣品的磁通量變化量ΔΦ隨勵磁電壓的增加而快速的增加,即ΔΦ/ΔU較大,導致檢測電壓在樣品初始磁化時隨勵磁電壓增加而快速增加;當樣品內部磁化逐步達到飽和狀態,導致檢測線圈的磁通量變化量隨勵磁電壓的變化量的增幅變慢,即ΔΦ/ΔU降低,從導致檢測電壓的增幅變緩. 另一方面,樣品在彈性形變區域內,檢測電壓隨應力的變化很小,幾乎接近于線性變化的關系,但在拉應力接近屈服應力時,檢測電壓大小隨應力的增加而快速減小.
3 結 論
與傳統探頭相比,九腳探頭與試件接觸面積小,勵磁探腳關于中心對稱分布,能夠產生更強、更均勻的勵磁磁場,提高了實驗精度和實驗效率. 利用九腳探頭測試了Q235,Q255和Q345#鋼材在不同應力條件下的檢測電壓隨勵磁電壓變化的曲線,實驗表明,在相同的勵磁電壓條件下,應力達到試件的屈服點之前,探頭的檢測電壓同應力呈線性關系,當應力接近屈服點時,檢測電壓隨應力增加而快速變小,呈非線性關系. 利用該特點,可以快速檢測工程中的鐵磁部件受力狀態.

