隨風(fēng)潛入夜，“頓悟”巧發(fā)生

江蘇省通州灣三余初級中學(xué) 姜海平

新課程標(biāo)準(zhǔn)認(rèn)為學(xué)生是學(xué)習(xí)的主人，因此教師要重視他們的自主學(xué)習(xí)，重視他們獨特的思考過程感受和思維迸發(fā)的體驗。因此，啟發(fā)“頓悟”發(fā)生的初中數(shù)學(xué)課堂成了學(xué)生生成素養(yǎng)的理想課堂。一般地，讓“探究在先，合作在后”“學(xué)的前移，而教的后置”等學(xué)習(xí)方式，都是“頓悟”產(chǎn)生的絕佳時機(jī)。

一、在情境中，給“頓悟”提供畫面

心理學(xué)家研究表明，在熟悉的情境里，人們的思維更活躍，從頓悟中能催生新的認(rèn)知。現(xiàn)在的班級基本是一個大熔爐，各地方的學(xué)生都有。而不同地域的學(xué)生接觸的事物往往不同，教師呈現(xiàn)的情境就應(yīng)該是他們比較了解的甚至是比較熟知的。教師在設(shè)置情境時，可以用學(xué)生熟悉的認(rèn)知進(jìn)行導(dǎo)入。比如在講勾股定理時，教師設(shè)置這樣的情境：據(jù)說科學(xué)家準(zhǔn)備將勾股定理作為與外星人進(jìn)行交流的暗號，你能將這一暗號運用到下面這道題當(dāng)中嗎？學(xué)生對外星人的相關(guān)傳聞有所了解，這是舊知；對勾股定理，特別是對它的運用不是很了解，這是新知。這樣的情境足以調(diào)動學(xué)生解題的興趣，它既告訴學(xué)生勾股定理的重要性，也提醒學(xué)生這題的思維焦點。“問題是接生婆，它能幫助新的思維的誕生”，但情境要有一個從“舊”向“新”漫溯的過程，以這題為例：現(xiàn)有長方形紙片一張，長19cm，寬15cm，需要剪去邊長多少的小正方形，才能做成底面積為77cm2的無蓋長方體的紙盒？教師先讓學(xué)生拿出一張紙片，按照要求裁剪成題目中的樣子，然后再控制好尺寸，做成一個盒子。這樣題目就變成了情境題，給學(xué)生“頓悟”提供真實的畫面，要求邊長，學(xué)生先將邊長設(shè)為xcm，這是他們練習(xí)數(shù)學(xué)時的一個定勢思維。當(dāng)學(xué)生看著折疊的盒子，他們很快就能推測出新的長和寬，這個“頓悟”在有了具象之后就一目了然了。

學(xué)生列出方程為(19-2x)(15-2x)=77，最終算出結(jié)果，當(dāng)x=13時，19-2x＜0，他們看著情境，也知道不符合題意，因而就剩下x=4。情境給“頓悟”的時間，也給學(xué)生思維轉(zhuǎn)換的空間。“頓悟”是學(xué)生慢慢揣摩的過程，是他們將推測付諸實施的過程。情境在某種程度上可以驗證“頓悟”的結(jié)果，同時也會讓學(xué)生在日后的學(xué)習(xí)中將情境印入頭腦，不需要具體的操作就會浮現(xiàn)在他們眼前。

二、在合作中，給“頓悟”提供幫助

現(xiàn)在對數(shù)學(xué)的考查大多集中在對學(xué)生素養(yǎng)與能力的測試，因而問題具有開放性，自然也就有一定的難度，教師可以結(jié)合學(xué)生的認(rèn)知規(guī)律安排小組討論，做到人人能有話說，人人參與，這樣可防止個別優(yōu)生的思維代替其他學(xué)生思維，進(jìn)而使所有學(xué)生在認(rèn)識上都有一個“頓悟”的過程，都能迸發(fā)智慧的火花。要想讓“頓悟”實實在在地在每個學(xué)生身上發(fā)生，教師就要組織好、引導(dǎo)好討論， 做到及時反饋。討論的過程也是醞釀“頓悟”的過程。討論的過程也是學(xué)生合作的過程，思維碰撞的過程，也是學(xué)生產(chǎn)生新思維的過程。討論當(dāng)然離不開教師的指導(dǎo)，因此不能盲目地出示問題后就讓學(xué)生討論，這樣會變成學(xué)生的自言自語，或者成為好生的個人表演。老師要有計劃地參與小組的討論，在思考方法、提問方法、意見方法等方面加以指導(dǎo)，長期下去，學(xué)生便能掌握討論方法，討論技巧，從而使“頓悟”更好地形成。已知：如圖，Rt△ABC中，∠ACB=90°，AC=BC，點D為AB邊上一點，且不與A、B兩點重合，AE⊥AB，AE=BD，連接DE、DC。（1）求證△ACE≌△BCD； （2）猜想△DCE是什么三角形。

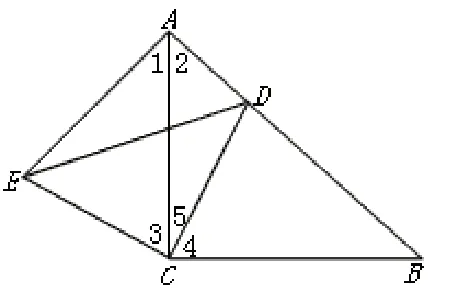
對于第一問，不再贅述。說一說第二問的“頓悟”過程。當(dāng)學(xué)生將題目中涉及的角用數(shù)字一一標(biāo)出來之后，在小組討論的過程中他們發(fā)現(xiàn)這很有可能就是等腰直角三角形。因為在第一小題中已經(jīng)證明了邊相等，題目中又出現(xiàn)了直角三角形，這個三角形可能也是。小組合作集中了集體的智慧，也讓“頓悟”能走上思維的快車道，在提高解題效率的同時，為之后題目中的“頓悟”提供更多思路。合作之后，就是學(xué)生自我解題的過程，學(xué)生說因為△ACE≌△BCD，所 以CE=CD，∠3=∠4，因 為∠4+∠5=90 °，所 以∠3+∠5=90°，所以∠ECD=90°。

三、在追問中，讓“頓悟”走向深刻

讓學(xué)生順著問題的脈絡(luò)自己去尋找可能的結(jié)論。傳統(tǒng)的習(xí)題總是規(guī)定好結(jié)果，讓學(xué)生進(jìn)行演算，或者證明，答案往往都是唯一的，但為了加強(qiáng)對學(xué)生思維靈活性的訓(xùn)練，教師可以設(shè)置開放性的問題。讓學(xué)生自己去尋找問題，或者在問題中讓學(xué)生自己去尋找答案。這給學(xué)生思維放飛的空間，給適合“頓悟”生長的土壤。在學(xué)生解決完一個問題之后，教師可以接著追問一個問題，使“頓悟”繼續(xù)發(fā)生。在學(xué)生回答不出問題之后，教師可以補(bǔ)問一個問題，讓問題進(jìn)一步明晰，進(jìn)一步對接學(xué)生的能力范圍。比如說教師在講解梯形的時候，先提出這樣一個問題：兩個完全一樣的梯形可以拼成一個平行四邊形嗎？學(xué)生在座位上比劃的同時，教師拋出第二個問題，拼成的平行四邊形的高和原梯形的高有什么關(guān)系？學(xué)生繼續(xù)“頓悟”，學(xué)習(xí)走向深層，問題由表及里。接著教師又問：拼成的平行四邊形的底和原梯形的哪兩條線段有關(guān)？拼成的平行四邊形的面積和原梯形面積有什么關(guān)系？每一個問題都是在原有問題上的一次升華，都是為了讓學(xué)生在“頓悟”的過程中不至于停留在事物的表面，都是讓學(xué)生養(yǎng)成深層思維的習(xí)慣。學(xué)習(xí)數(shù)學(xué)最終目的不是為了解題，而是要在解題的過程中優(yōu)化思維品質(zhì)。

“頓悟”就是學(xué)生處于“憤悱”的狀態(tài)，在似懂又非懂，在有所知又非全知的狀態(tài)下，通過給學(xué)生做鋪墊，調(diào)動其學(xué)習(xí)的主動性， 發(fā)展其思維的核心素質(zhì)。因此，“頓悟”就是在學(xué)生掌握數(shù)學(xué)思維基礎(chǔ)認(rèn)知之后，形成基本方法，進(jìn)而提升思維的品質(zhì)，即，頓悟的過程也是直觀和感性思維、理性和科學(xué)思維、逆向和批判思維發(fā)展的過程。