基于Kriging模型和模擬退火粒子群算法的結構有限元模型修正

康俊濤 柯志涵 胡 佳

(武漢理工大學土木工程與建筑學院 武漢 430070)

0 引 言

工程中，實際結構現場試驗響應值與建立的結構有限元分析模型計算值往往存在誤差，需要對建立的初始有限元模型進行修正.模型修正在結構的性能評價[1]、健康監測[2]、損傷識別[3],以及驗證結構設計等領域中廣泛應用.有限元模型修正，是建立的初始有限元分析模型利用結構現場試驗響應值來修正模型計算值，使得修正后模型計算值與結構試驗值誤差最小.直接調用有限元軟件進行模型修正存在計算效率低，不易于二次開發等缺點[4-5].采用代理模型結合智能算法進行模型修正，克服了修正過程中大量調用有限元模型計算的不足.代理模型是利用顯式函數式擬合構造出結構有限元模型設計參數與其響應之間復雜的隱式關系的一種數學模型，其避免了復雜的有限元計算.任偉新等[6]在模型修正中采用代理模型，提高了修正的效率.

常用的代理模型有響應面方法[7](response surface method,RSM)、徑向基函數[8](radical basis function,RBF)、Kriging模型[9]等.其中Kriging模型由于存在隨機過程，更適合于復雜非線性的結構輸入、輸出模型，具有非常高的精度.

模型修正問題歸根結底可以看成優化問題，常結合優化算法求解.基本粒子群算法(particle swarm optimization，PSO)的思想源于模擬鳥群的覓食行為，是由Kennedy等[10]提出的一種群體協作隨機搜索算法.其實現容易、概念簡單、魯棒性強、收斂速度快，在結構模型修正[11]、優化設計[12]等領域得到廣泛應用.但PSO在搜索過程中容易陷入局部極值解，存在早熟等缺點[13].而模擬退火粒子群算法[14](simulated annealing particle swarm optimization，SimuAPSO)在搜索過程中受溫度參數的控制而避免陷入局部極值解，能夠較快的收斂到全局最優解,提高計算效率.

1 Kriging函數模型及試驗設計

1.1 Kriging函數模型

Kriging函數模型是由回歸模型與隨機過程相加而成.其形式為

y(X)=fT(X)β+z(X)

(1)

式中：X為維度為d的設計參數[x1,x2,…,xd]；y(X)為模型響應值；fT(X)β為回歸模型，fT(X)=[f1(X),f2(X),…,fm(X)]，β=[β1,β2,…,βm]T為回歸矩陣，常用二次無交叉項多項式模型為

(2)

式中：z(X)為均值為0協方差為σ2的隨機過程，提供模擬的局部近似.z(X)中任意兩個參數的協方差表示為

Cov(z(X)z(ω))=σ2R(X,ω)

(3)

式中：R(X,ω)為任意兩個樣本點X和ω之間的變異函數,其一般形式為

(4)

式中：Rj(dj)為變異函數的核函數，通常采用高斯函數,則變異的函數形式為

(5)

式中：θj為計算空間相關函數中大于0的系數；n為變異的維數.假設有N個樣本點，響應陣和多項式陣分別為Y=[y(X1)…y(XN)]，F=[fT(X1)…fT(XN)]T，得到β和σ2值為

(6)

(7)

式中：空間相關矩陣為

(8)

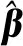
(9)

式中：|R|為矩陣R的行列式值；θ值可以通過遺傳算法、模式搜索、粒子群算法等優化方法得到.確定了θ1,θ2,…,θd的值，最后利用已得到的模型系數和變異函數參數，得到最好線性無偏估計值為

(10)

1.2 試驗設計

試驗設計是構建Kriging函數的基礎，對修正參數進行試驗設計抽樣得到樣本點作為輸入集，并將樣本點代入有限元計算得到結構響應作為輸出集，根據輸入和輸出集擬合得到Kriging函數.因此試驗設計方法直接影響構造Kriging模型的精度，同時也是決定結構有限元計算量的主要因素.

本文樣本抽樣方法選用的是由Timothy 等[15]提出的一種基于分層抽樣思想的拉丁超立方設計(LHD).LHD將變量空間分成n個子區間，每個子區間概率相同且互不重疊,然后分別獨立隨機地在每個子區間內采樣一次，以保證樣本點的均勻性.拉丁超立方抽樣的樣本為

(11)

式中：n為樣本點數；i為水平數；j為維數；dij為1到n的獨立隨機排列數；eij為[0,1]之間的隨機數.

2 模擬退火粒子群算法

模擬退火粒子群算法是一種源于固體退火原理的啟發式搜索算法，其步驟如下.

步驟1隨機初始化各粒子的位置與速度.

步驟2評價每個微粒的適應度，將第i個微粒所經歷的歷史最好點儲存在pi中，將所有pi中的最優值儲存在pg中.

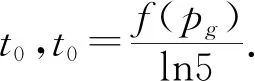
(12)

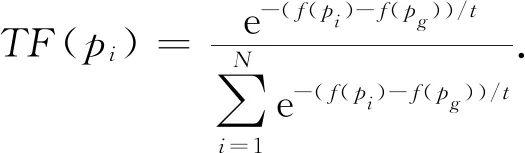
(13)

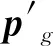
vi(t+1)=φ{vi(t)+c1r1[pi-xi(t)]+

c2r2[pg-xi(t)]}

(14)

xi(t+1)=xi(t)+vi(t+1)

(15)

(16)

式中：vi(t)為粒子溫度t時的速度；xi(t)為粒子溫度t時的位置；ω為慣性權重；pi為每個粒子經過的歷史最優點；pg為所有粒子經過的全局最優點；c1、c2為學習因子；r1,r2為擾動因子，r1,r2∈[0,1].

步驟6計算各微粒新的目標值,更新各微粒的pi值及群體的pg值.

步驟7進行退溫操作，tk+1=λtk，其中0<λ<1.

步驟8若滿足運算精度或迭代次數等停止條件時，輸出當前最優值，搜索結束，否則返回步驟4繼續搜索.

3 桁架數值模擬算例

通過一空間桁架進行數值模擬，對設計參數人為給定攝動量，構造Kriging函數模型代替空間桁架Midas結構，結合SimuAPSO進行尋優，完成對桁架結構的修正.

具體修正流程圖見圖1.

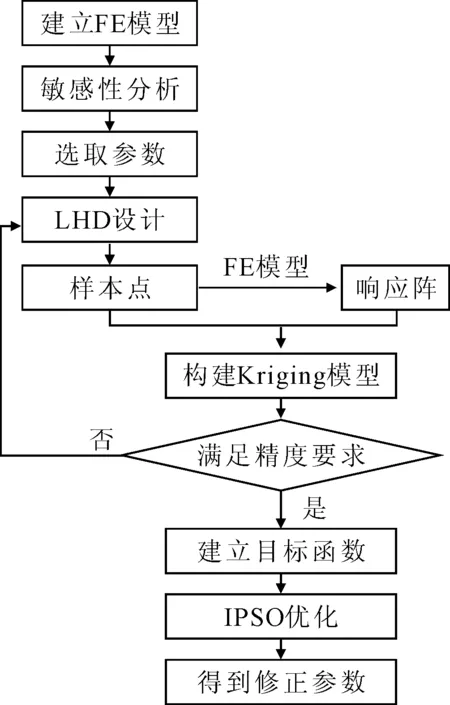
圖1 模型修正流程圖

3.1 桁架模型

利用一個空間桁架結構作為算例驗證構建Kriging法用于模型修正的可行性，見圖2.桁架豎直和水平方向每根桿單元長度均為0.5 m，總長度為2 m、寬度為0.5 m、高度0.5 m，彈性模量為2.06×105MPa，采用管形截面,外徑為16 mm，管壁厚2.5 mm，截面面積為7.85×10-4m2.桁架材料的初始密度(用ρ表示)為7 852 kg/m3,用Midas建立空間桁架模型見圖3.

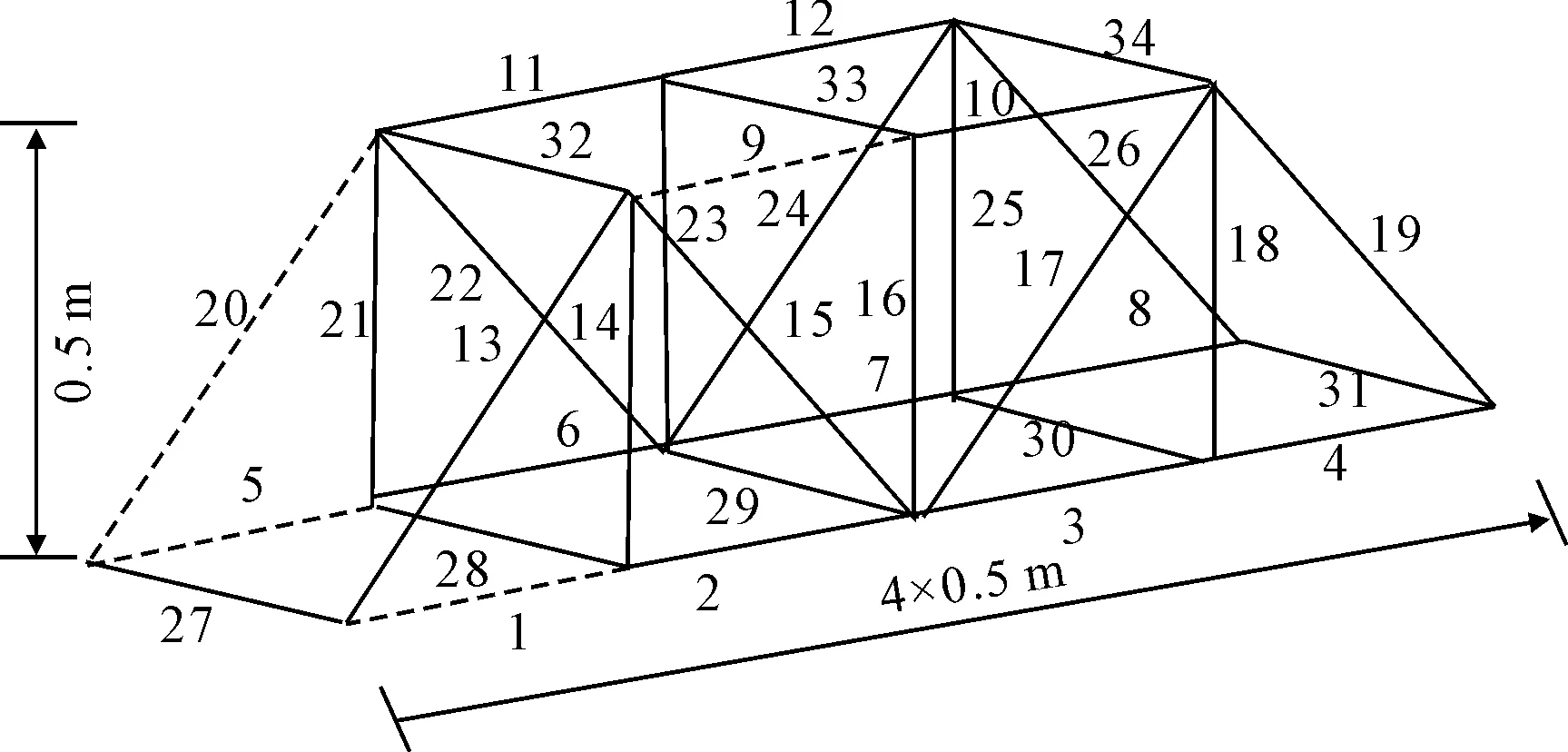
圖2 空間桁架結構

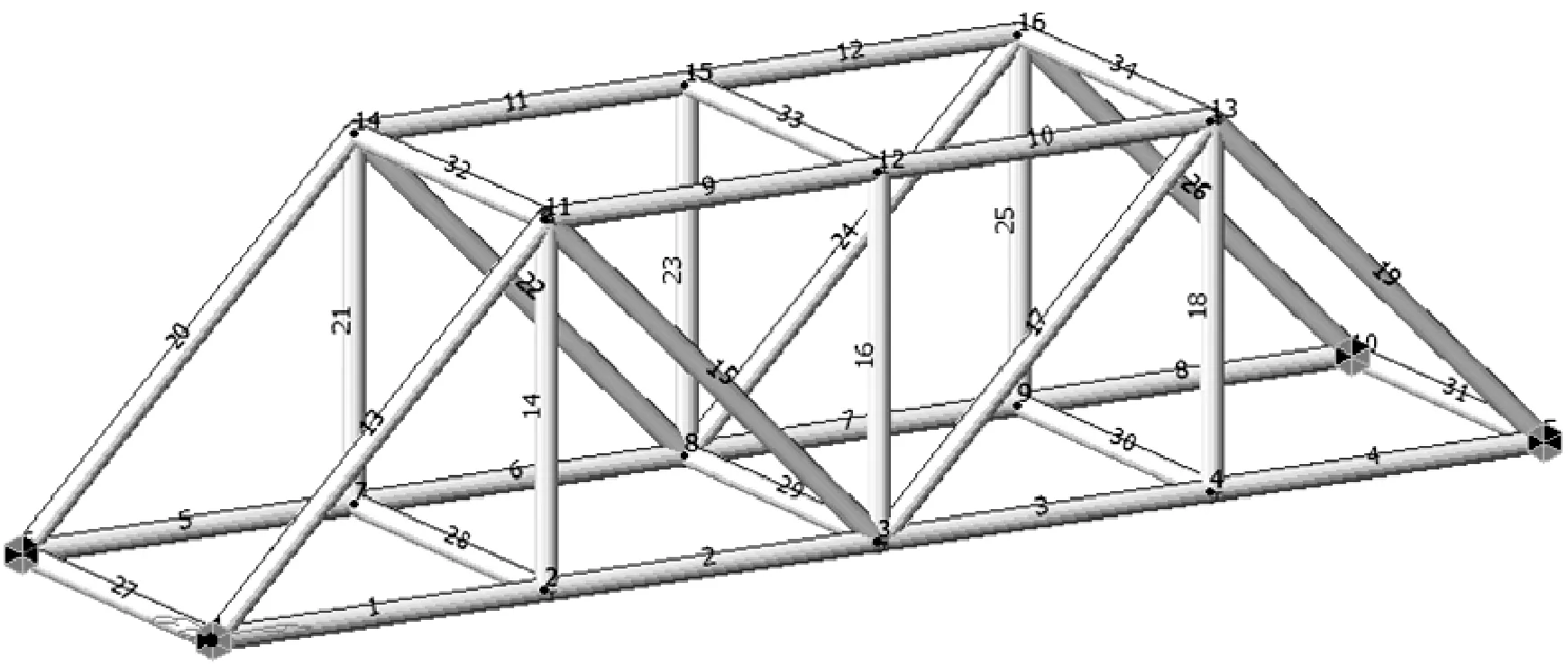
圖3 Midas建立的空間桁架模型

桁架由34個桿件單元和16個節點組成，節點1約束住三個平動自由度，節點5，6約束住z方向平動自由度，節點10約束住y，z方向平動自由度，且該四個節點均約束住繞x，z軸方向的轉動自由度.對34根桿件的密度參數進行擾動，代入有限元模型計算其響應，經過敏感性分析，選取ρ1，ρ5，ρ9，ρ20四個敏感參數，人為地擾動這四個參數數值，ρ1增加20%至9 420 kg/m3，ρ5增加15%至9 028 kg/m3，ρ9增加30%至10 205 kg/m3，ρ20增加10%至8 635 kg/m3.未損傷模型代表初始模型，擾動后的損傷模型代表實際模型，經過Midas空間桁架模型計算得到實際模型與初始模型的前6階頻率見表1.

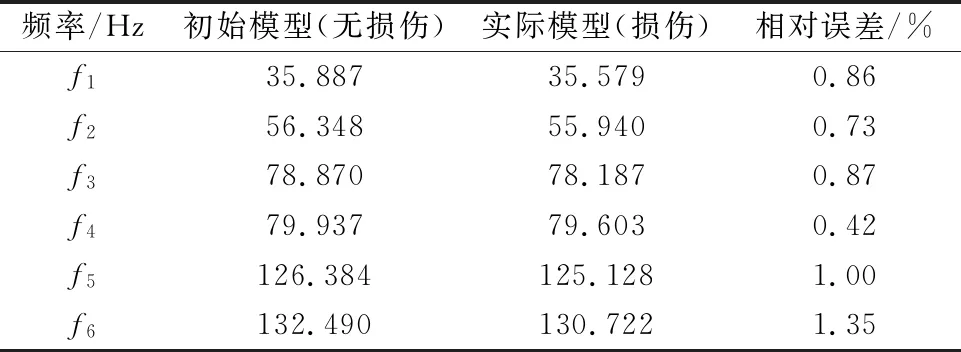
表1 初始模型和真實模型的前6階頻率

3.2 試驗設計

采用LHD抽樣方法，對選取的ρ1，ρ5，ρ9，ρ20這四個參數進行抽樣40次得到試驗點并代入有限元模型中計算得到對應的頻率數據.設計參數的變化范圍為±50%，即抽樣點密度下界為3 925 kg/m3，上界為11 775 kg/m3.將ρ1，ρ9抽樣的樣本散點圖繪于圖4，試驗點均勻地散布于輸入參數空間中.

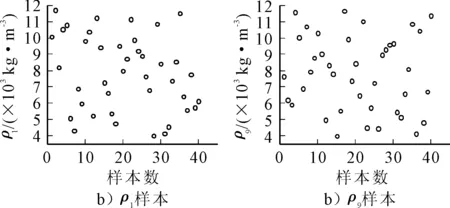
圖4 利用LHD得到的ρ1，ρ9樣本散點圖

3.3 構建Kriging模型及精度檢驗

LHD抽樣得到樣本點作輸入集，利用Midas計算得到的前六階頻率作輸出集，構建Kriging模型.選取桿件單元1和9的密度參數作為自變量，桿件單元5和20的參數值為初始值不變，做Kriging函數擬合圖，見圖5.由圖5可知,構造的Kriging函數響應面平滑，圖6是構建Kriging模型的均方誤差圖，其MSE值數量級在10-4，表明擬合構建的Kriging函數設計參數估計值與真值誤差較小，精確度較高，能代替有限元模型.

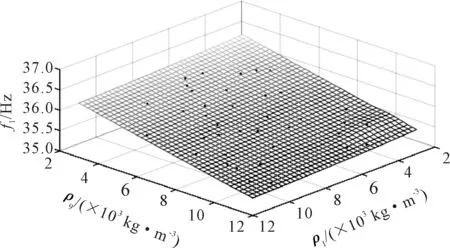
圖5 頻率f1和密度ρ1，ρ9之間的函數擬合圖

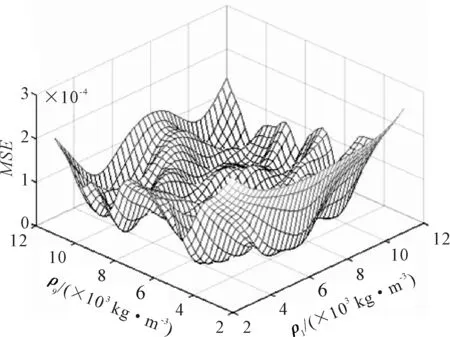
圖6 Kriging函數的均方誤差圖

3.4 構建目標函數

以構建的Kriging代理模型得到的前六階頻率與實際結構的前六階頻率相對誤差的平方和作為目標函數.

(17)

式中：fkrigi為構建的Kriging代理模型得到的第i階頻率響應；fri為實際損傷結構的第i階頻率響應.

3.5 SimuAPSO優化

SimuAPSO算法參數設置如下：初始粒子總數為100，迭代次數200次，粒子維數四維，個體認知部分權重與社會認知部分權重均取2.05.優化結果及誤差見圖7.由圖7可知，四個參數的初始值為7 850 kg/m3,經模擬退火粒子群優化得到的修正值分別為9 807，8 521,10 147,8 901 kg/m3,損傷結構的真實值分別為9 420,9 028，10 205,8 635 kg/m3.圖7中條形圖上數字表示修正值與真實值的相對誤差，可見最大相對誤差為5.61%，最小相對誤差為0.57%，滿足誤差要求.

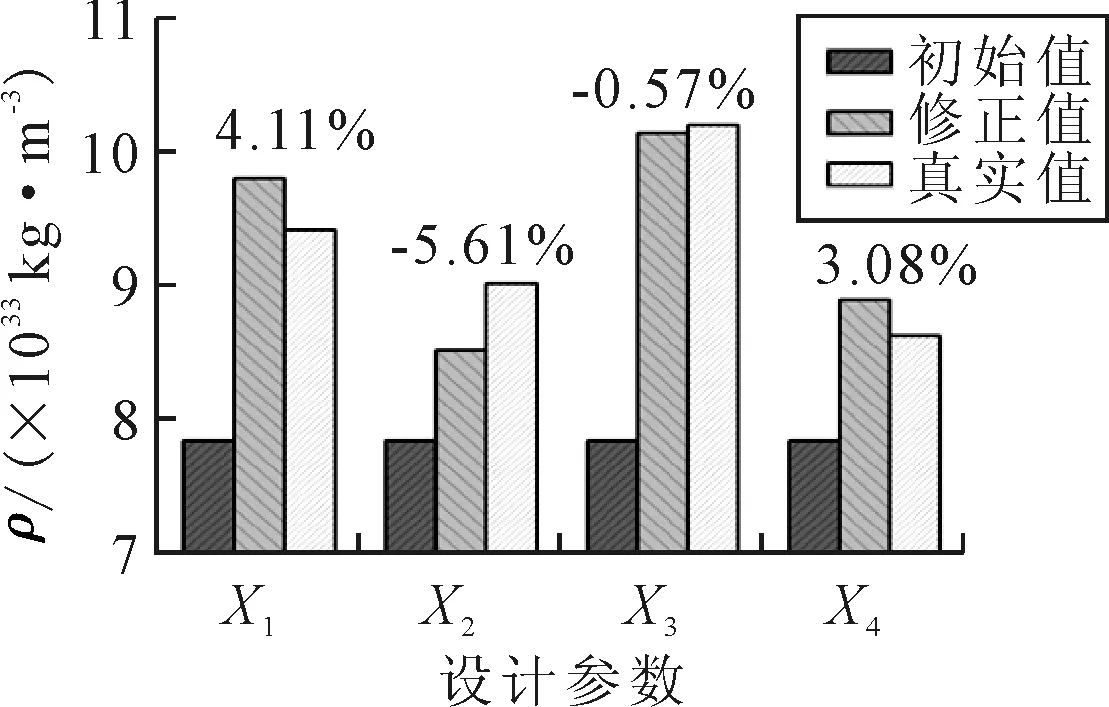
圖7 模擬退火粒子群算法參數修正圖

圖 8為模擬退火粒子群算法和經典粒子群算法對目標函數的最優解進化的曲線圖.

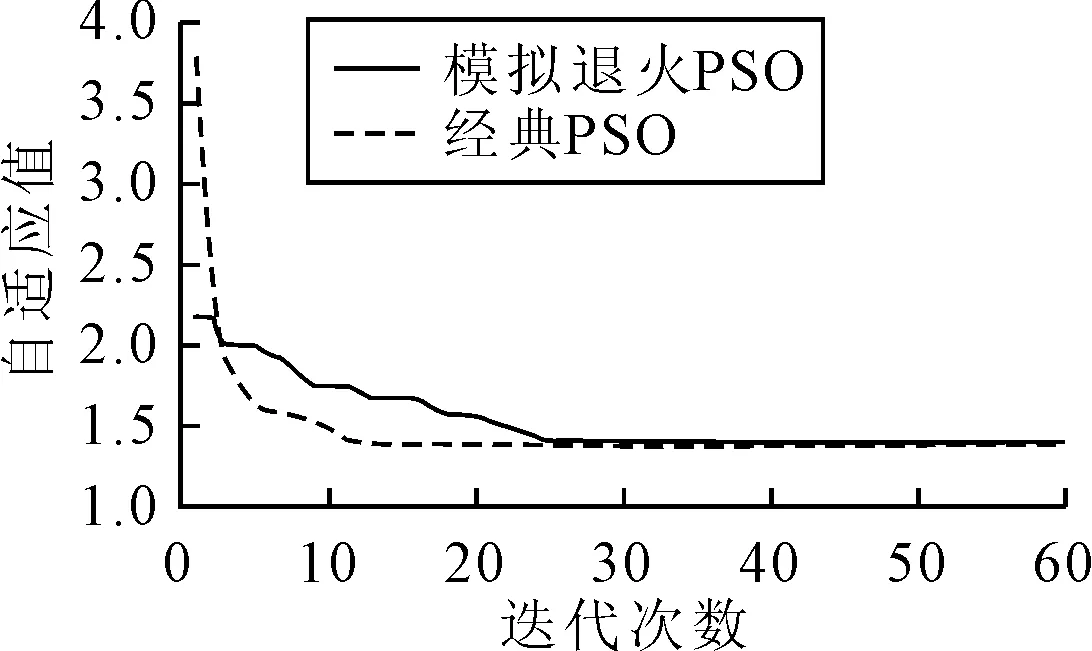
圖8 兩種算法對目標函數的最優解進化曲線圖

由圖8可知，兩種算法修正后的目標函數值基本一致.但SimuAPSO優化效率較高，可以避免陷入局部極值解，更快的收斂到全局最優解.標準粒子群算法得到最優解的迭代次數需要20次以上，而本文采取的模擬退火粒子群將迭代次數縮小到10次左右，提高了優化效率.

4 結 論

1) 基于Kriging代理模型的結構有限元模型修正避免了重復調用有限元進行計算，縮短了運算時間.

2) 基于MATLAB編程的Kriging模型修正過程易于與優化算法相結合，采用模擬退火粒子群算法，較快收斂到全局最優解，顯著提高優化效率.

3) 通過空間桁架算例表明，基于Kriging代理模型，結合模擬退火粒子群算法實現有限元模型修正是一個行之有效的方法.在結構優化設計、模型修正與確認、損傷識別等工程領域有很好的應用價值.