航天服硬式髖關節耦合機構建模與運動分析

王振偉,程 鵬,徐利梅,謝曉梅,李學生,林丹蘭

(電子科技大學航空航天學院,成都611731)

1 引言

航天服是航天員的重要生命保障和支撐系統。星表作業要求航天服的關節系統具備較好的運動性和靈活性,以完成行走、維修、搬運等任務[1]。通常,航天服內維持一定的壓力,服內壓力會給航天服關節彎曲運動帶來較大阻力,降低星表作業的效率。通常采用旋轉軸承[2-3]、活動框架[4-5]和織物褶皺[4-6]等結構來提高關節的活動性能,如美國“水星”航天服、“雙子星”航天服、MARK III、Z-1、Z-2,俄羅斯“海鷹”航天服,中國“飛天”航天服等。圍繞航天服關節系統,目前在結構設計[7]、阻力/阻力矩分析[8]、動態性能計算[9]、人機交互性能[10]等方面開展了一系列研究。隨著月球、火星、土星等星表探測的發展對航天服下肢關節系統提出了更高的要求。

目前,航天服下肢髖關節研究工作多數集中在制造加工、試驗測試等方面。圍繞航天服硬式髖關節的運動分析,本文提出一種3自由度混合機構模型,闡明大腿-髖關節耦合機構的運動原理,完成機構運動自由度分析,建立機構的運動方程。

2 髖關節的機構建模

2.1 髖關節機構的設計模型

本文基于航天服概念設計模型如圖1所示。它是一種軟硬復合式航天服,由軟、硬兩種類型關節構成,具體參見文獻[11]。其中,硬質髖關節是本文的主要研究對象,其設計模型如圖2所示。為滿足大腿3自由度運動需求,提出由球冠形關節串聯而成的髖關節概念設計方案。每個髖關節構件都以半球形薄殼體為基礎,通過切削球體來獲得具有一定斜面的球冠形殼體；各髖關節構件通過軸承依次首尾連接,組成可相對旋轉運動的串聯機構；在大腿運動過程中,每個髖關節構件圍繞自身軸線旋轉,從而改變髖關節構件的空間位姿,實現髖關節和大腿的同步運動。

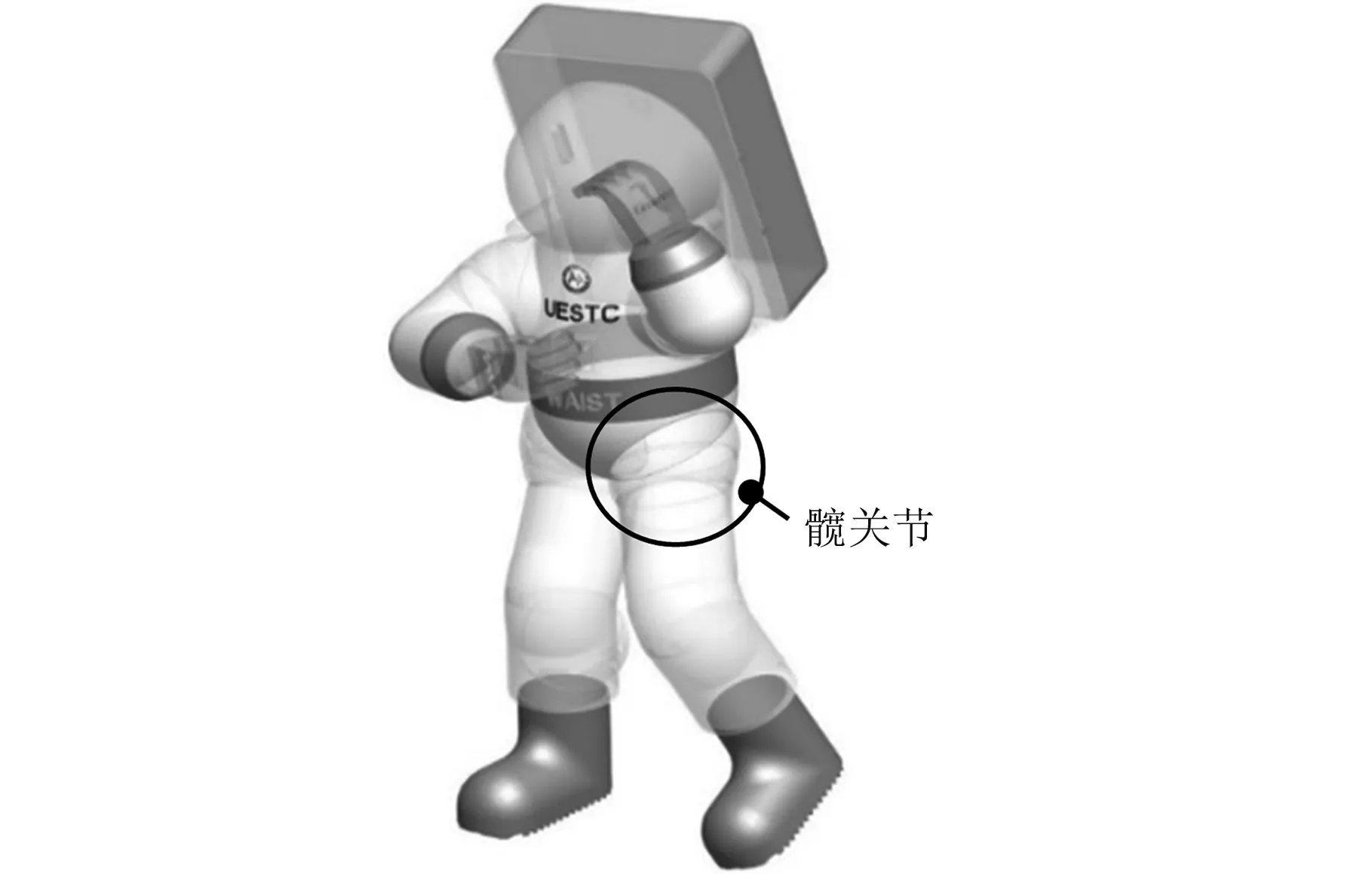
圖1 航天服的概念設計模型Fig.1 Conceptual design model of spacesuit

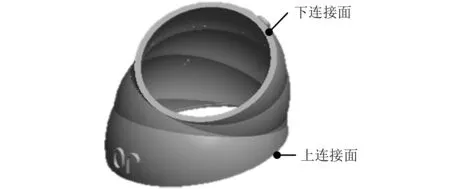
圖2 髖關節機構的設計模型Fig.2 The design model of hip joint mechanism

髖關節的設計參數包括球殼半徑ri和傾角ai,如圖3所示。由于各髖關節構件采用串聯連接方式,當初始髖關節構件的半徑r1由設計任務給定時,其它髖關節構件的半徑ri+1可由相鄰髖關節構件的半徑ri和傾角ai計算獲得,即ri+1=ri×cosai。因此,髖關節機構的設計參數主要是指各髖關節構件的傾角ai。同時,考慮到連接軸承的尺寸和體積相對較小,對髖關節機構的運動分析影響不大,因此忽略連接軸承的建模與表達。

圖3 髖關節構件的設計模型Fig.3 The design model of hip joint component

根據大腿的擺動要求建立髖關節機構的3個約束條件：

1)自由度約束。為了滿足人體大腿的運動需求,建議航天服髖關節機構具備3個以上的自由度。為了運動分析的方便,避免運動解的不確定性,擬定髖關節具有3個自由度。

2)正交約束。在人體大腿擺動過程中,需要保證髖關節機構的“下連接面”始終與大腿中心軸線保持正交,以避免航天服下肢系統對人體大腿運動的干涉、阻礙和碰撞,甚至是損傷。

3)固定約束。通常,人體大腿關節點固定不動,它不隨大腿擺動而改變位置。因此,要求航天服髖關節鉸點具有位置保持性,機構設計時應明確給出人體大腿關節位置,并維持不變。

2.2 大腿-髖關節的機構模型

髖關節構件是關于中心剖面對稱的球殼結構,將圖3所示髖關節構件的設計模型進行抽象,在中心剖面上建立相應的髖關節構件數學模型如圖4。具體而言,將髖關節構件簡化為由上連接副和下連接副組成的連桿模型。其中,上連接副和下連接副分別位于髖關節構件的上/下連接面的轉動中心處,它們都是轉動副,是對連接軸承的簡化且與對應端面保持正交。這樣,髖關節構件數學模型的表達參數包括ai、di和ri。其中,di是髖關節構件的上/下連接面的圓心距離,或稱為連桿的長度。在運動分析時,可用一個矢量表征。

目前研究大都只考慮髖關節構件的本體建模與計算,忽略了人體大腿和髖關節機構的相互耦合作用。為此建立大腿-髖關節耦合的機構原型,如圖5所示。

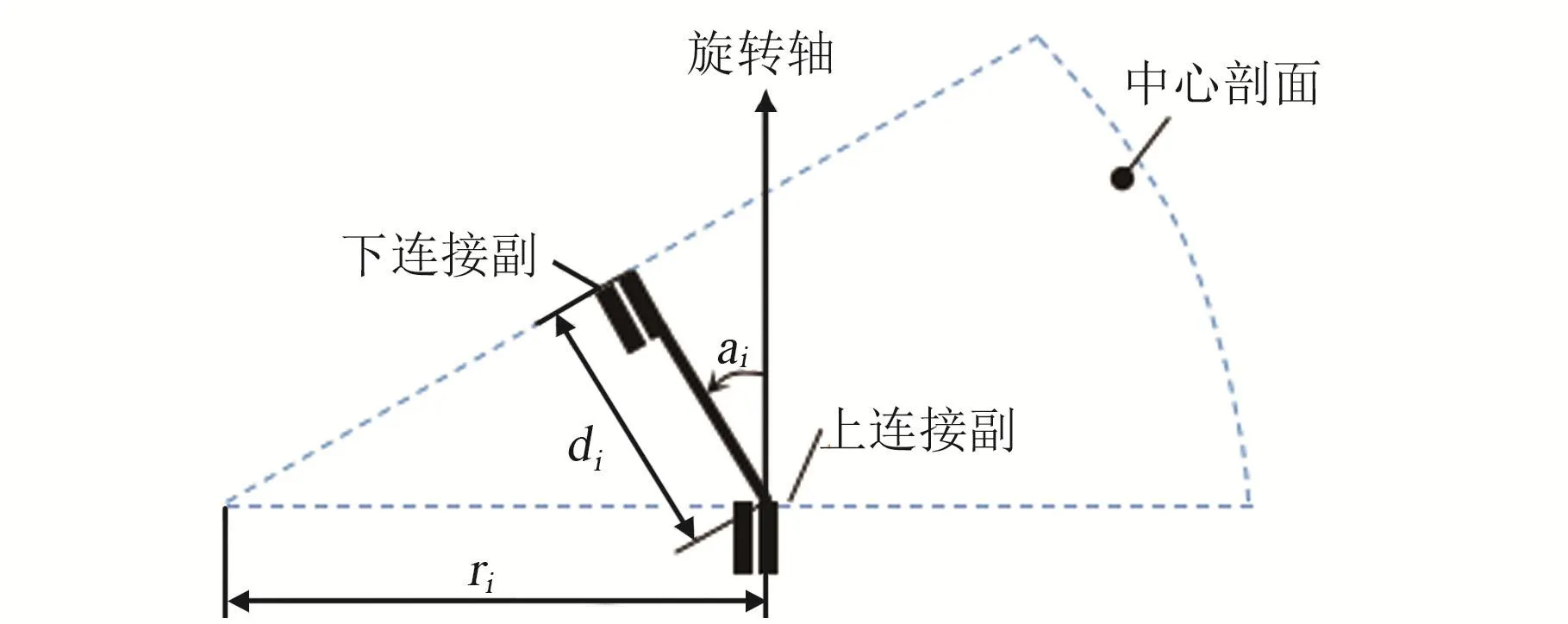
圖4 髖關節構件的參數模型Fig.4 Parameter model of hip joint component

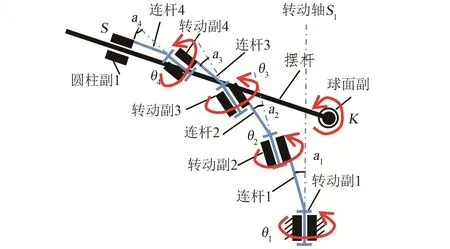
圖5 大腿-髖關節耦合的機構原型Fig.5 Prototype of thigh-hip joint coupling mechanism

該機構原型包括4個旋轉副、1個球面副、1個圓柱副、4個連桿和1個擺桿。其機構構型是一個串并混合的閉合式機構。其中,大腿簡化為具有3個旋轉自由度的擺桿,K點為大腿擺桿的關節鉸點。大腿擺桿lKS與末端髖關節構件的下連接副采用了圓柱副連接,從而保證了髖關節機構與大腿軸線的正交約束條件。同時,將初始髖關節構件抽象為與機架的轉動連接。

對于大腿-髖關節機構的自由度,由圖5可見,大腿-髖關節機構包括5個構件,分別是連桿1、連桿2、連桿3、連桿4和擺桿,并具有4個轉動副、1個圓柱副和1個球面副。初始髖關節構件雖然與航天服上身相連,但對大腿運動沒有影響,因此將航天服上身看作是固定機架。在三維空間中,一個構件具有6個自由度。1個轉動副提供5個約束,具有1個旋轉自由度。1個圓柱副提供4個約束,具有1個旋轉自由度和1個移動自由度。1個球面副提供3個移動約束,具有3個旋轉自由度。對于圖5機構而言,其自由度計算如下：5個構件共具有5×6=30個自由度,4個轉動副共具有4×5=20個約束,1個圓柱副具有4個約束,1個球面副具有3個約束。因此,“大腿-髖關節機構”自由度為30-20-4-3=3。這與人體大腿的自由度數相同,滿足髖關節機構的自由度約束條件。

2.3 機構模型的簡化與確定

由圖5可見,大腿擺桿lKS需要完成空間3自由度旋轉運動。而且,要求轉動過程中,鉸點K的位置不發生變動,即固定約束。由幾何關系可知,當大腿擺桿lKS位于空間中任意2個不同方位的時候,只有鉸點K位于轉動軸S1上,才能滿足位置不變的固定要求。此外,為了進一步簡化機構模型,縮小機構模型的體積和規模,考慮到連桿1的長度對機構自由度沒有影響,令其長度為0,使得轉動副1和轉動副2重合,形成了復合轉動副。同時,令鉸點K與轉動副1重合。最終建立的大腿-髖關節的機構模型如圖6所示。

圖6 大腿-髖關節耦合的機構模型Fig.6 Model of thigh-hip joint coupling mechanism

綜上,大腿-髖關節機構模型滿足了人體大腿擺動的3個自由度要求。

3 大腿-髖關節機構的運動分析

3.1 大腿-髖關節機構的運動分析

為了完成髖關節機構的最終設計,需要根據設計需求和運動要求,通過計算分析來確定該機構模型的具體參數,包括所有連桿長度、角度和大腿擺桿鉸點K的位置。髖關節機構設計需求通常是給定的,包括相應髖關節構件的半徑參數和擺動角度范圍。令初始髖關節構件的半徑為r1,末端髖關節構件的半徑為r4,髖關節機構的擺動角度范圍為[0ad]。而且,上述參數r1、r4和ad通常為已知量,由設計要求直接給出。同時,根據人體大腿的自由空間運動需求,要求大腿擺桿lKS可以正確地運動到空間中任意位置。從數學分析角度來講,要求大腿擺桿lKS能夠完整地表達任意給定的空間方位矢量。

從運動形式來看,大腿-髖關節機構運動形式是空間定點轉動。為此,需要完成空間定點轉動的運動分解。本文將大腿擺桿lKS的空間運動分解為兩類轉動運動。第一類轉動運動是大腿擺桿lKS圍繞關節鉸點K的自由平面轉動。該類平面轉動可通過所有髖關節構件相對轉動來合成,需要保證大腿擺桿lKS能夠到達平面內的任意方位。第二類轉動運動是大腿擺桿lKS圍繞大腿-髖關節機構轉動軸S1的定軸轉動。該類運動需要一個旋轉副,以保證大腿擺桿lKS自由地轉動到空間任意方位。由上可見,第二類轉動運動較為容易,可以由復合轉動副來表征。下面主要討論第一類轉動運動。

根據機構模型建立大腿-髖關節機構的平面轉動幾何模型如圖7。線段OA和AB分別表示連桿2和連桿3,線段OS表示大腿擺桿lKS。根據髖關節機構的運動原理,線段OA圍繞y軸轉動,線段OH是線段OA定軸轉動的對稱位置；線段AB圍繞線段OA轉動,線段AC是它定軸轉動的對稱位置,其中,為了保證大腿擺動的連續性,點C須位于y坐標軸上。點A和B運動軌跡的xz面投影分別為圓C2和圓C1。線段OS上任意點P投影為點F,點B投影為點E。過F點做圍繞O點的圓C3,與圓C1相交于點Q。點Q是該狀態下點P對應運動點P′的投影點,這里稱點P′為影點。具體而言,當線段OS圍繞點O從起始位置OB順時針轉動a角時,相當于線段AB上點B的投影點E由點E沿著圓C1順時針轉動到點Q。同時,點Q與線段OA同步圍繞y軸沿著圓C3逆時針轉動到點F。這樣,通過線段AB和OA同步運動實現了線段OS的平面轉動。此外,由圖7可見點B和C是大腿擺桿的兩個極限運動位置,也是機構運動的不確定點。因此,應該在這兩個位置上設定必要的限位裝置,以避免不確定狀態的影響。

另外,線段AB和OA在線段OS轉動過程中始終保持長度不變。因此,夾角∠APO為一個常數。這樣,通過點B可做一個始終與線段OS正交的平面,其交點為T。由幾何關系可知,相應夾角∠TBC=a3-a2。根據正交約束條件,該夾角等于末端髖關節構件4的設計傾角a4。綜上,4個髖關節構件傾角設計參數中存在2個約束關系式：a1=0和a4=a3-a2。即當確定了a3和a2后,髖關節尺寸可以完整確定。

圖7 大腿-髖關節機構的平面轉動幾何模型Fig.7 Planar rotational geometry model of the thighhip joint mechanism

3.2 大腿-髖關節機構的運動方程

設線段OB為線段OS的初始方位,由3.1節運動分析可知,當線段OS圍繞點O轉動α角時,線段AB的對應轉角為θ,線段OA的對應轉角為φ。其中,在A向視圖內表達轉角θ,在xz坐標面內表達轉角φ。線段OA和AB的對應傾角為α2和α3。 當轉角α在0～2α2范圍內變化時,線段OS上點P在線段BC區間內移動,而且點P位置與轉角α之間形成一一映射,因此,可建立點P位置矢量關于轉角α的參數表達公式。在坐標系xyz中,設點B和C位置矢量分別為PB和PC,則點P位置矢量由公式(1)給出。

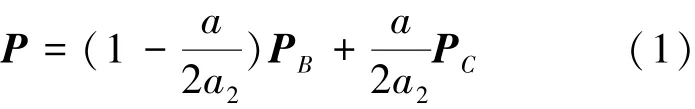
其中,

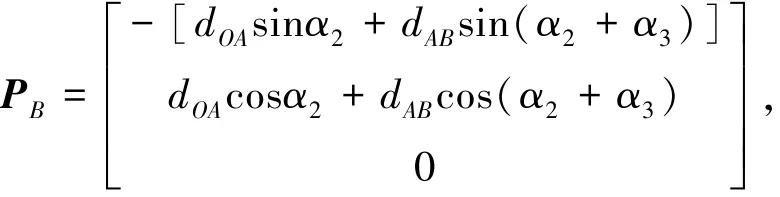
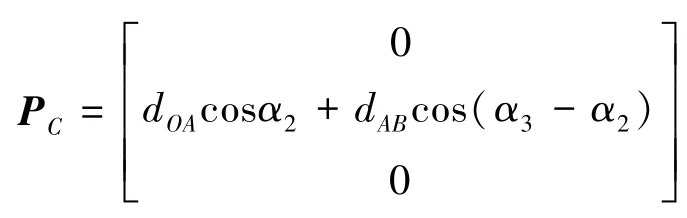
如前所述,影點P′在A向視圖的運動軌跡為圓形C4,在坐標面xz內的投影點為Q。由圖7可見,轉角θ和φ與影點及其投影點Q直接相關。若能求得影點P′在坐標系xyz中的位置矢量P′a,則投影點Q的位置坐標便可確定,進而求解轉角θ和φ。為了獲得影點P′在坐標系xyz中的位置矢量,需要進行坐標系xayaza到坐標系xyz的坐標變換。設上述兩個坐標系之間的變換矩陣為TC4-C1,根據坐標變換理論和矢量運算,可得影點P′在坐標系xyz中的位置矢量如式(2)。

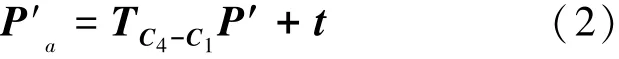
其中,

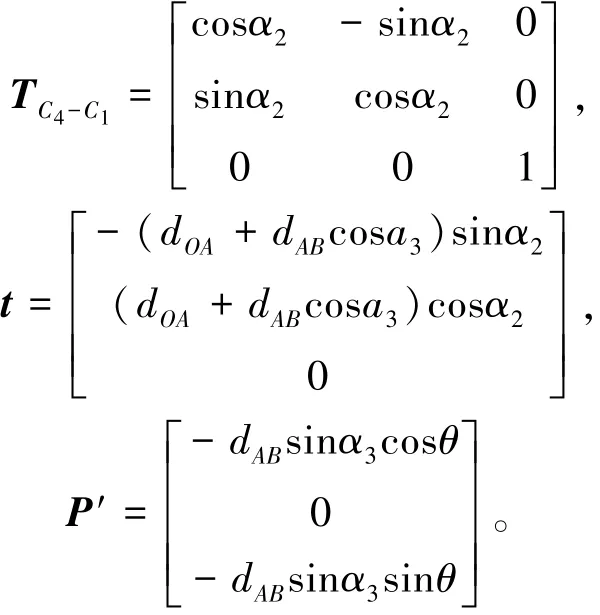
由圖7可見,隨著點P位置的不斷變動,投影軌跡圓C3半徑和點Q位置跟隨變化,使得轉角φ也在不斷變化。但是,圓軌跡的形狀不變,線段OQ和線段OF的長度相同。因此,點Q位置矢量長度就等于點P位置矢量的x坐標分量,從而得點Q位置矢量長度‖Q‖的計算公式(3)。

其中,是坐標軸x的單位向量。將點P位置矢量表達式(1)代入式(3),可得到點Q位置矢量長度‖Q‖的計算公式,如圖(4)、(5)所示：

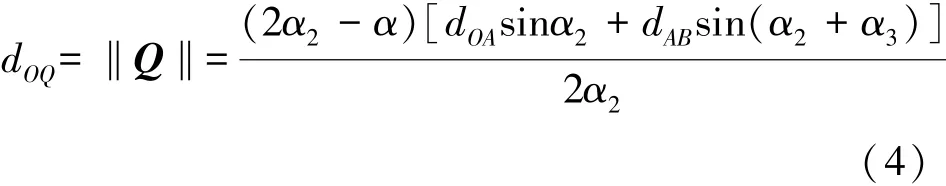
其中,

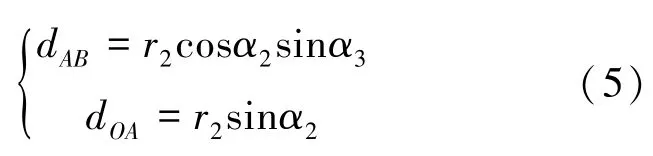
可得點Q位置坐標在坐標面xz內的表達式(6)。

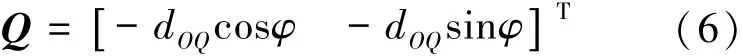
由于圓軌跡C1和圓C3在點Q處相交,因此,點Q位置矢量必將滿足影點P′在坐標面xz內的投影方程。將式(6)帶入式(2),可得式(7)。

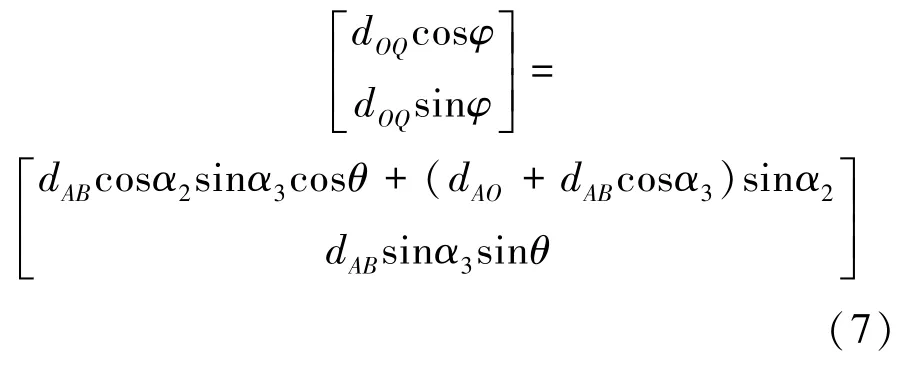
求解公式(7),可得轉動角度φ和θ表達式(8)。

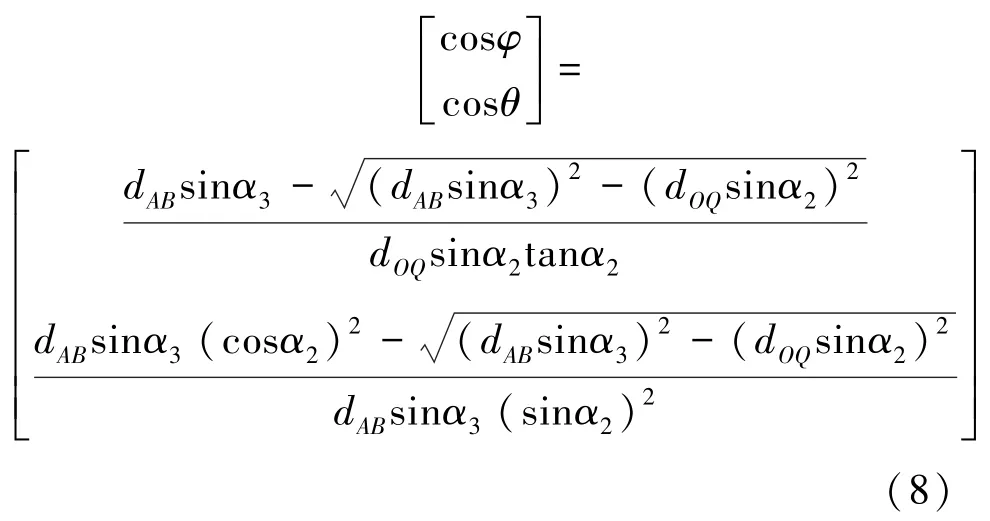
綜上,完成了大腿-髖關節機構運動方程的建立。給定傾角α2和α3后,可得到任意轉動角度α所對應的轉角θ和φ值。由式(5)可見,給定r2,式(8)只與α2和α3有關。 但是,大腿-髖關節耦合機構模型還需要滿足一定的幾何約束。下面詳細討論式(8)的具體求解流程。

3.3 大腿-髖關節的運動約束方程

如前所述,式(8)從幾何關系角度出發給出了運動方程,沒有考慮幾何要素之間的約束關系。由圖7可見,本文所提出的大腿-髖關節耦合模型存在2個幾何約束關系：第一個約束關系是點C的點線重合約束,3.1節已給出了“點C須位于坐標軸y上”的幾何約束；第二個約束關系是4個髖關節構件之間的連接關系約束。這2個約束關系將進一步簡化運動方程求解。下面,分別推導上述2個幾何約束的表達公式。

由圖7可見,要求點C始終位于坐標軸y上,以保證大腿擺桿(線段OS)運動空間的完整性。因此,在△OAC中,線段AC和線段OA之間始終滿足正弦定理,且線段AB和線段AC的長度始終相等。經進一步計算可建立由線段AB和OA長度表達的點線重合約束式,并將其表達髖關節半徑參數r2和傾角α2和α3的形式,如式(9)所示：

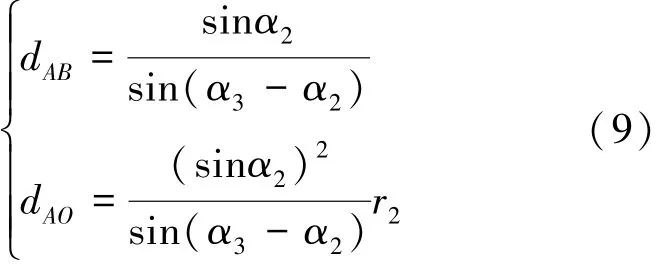
此外,由于各髖關節構件之間采用串聯連接關系。因此,各髖關節構件的半徑之間存在幾何約束,具體見2.1節。根據圖6中髖關節機構模型,初始髖關節構件的半徑r1=0,因此,將髖關節構件半徑尺寸r2作為初始設計值,并假設其為已知值。依據各髖關節構件的半徑約束關系,將線段長度dAB表達為髖關節半徑參數r2和傾角α2和α3的表達形式,如式(10)所示：

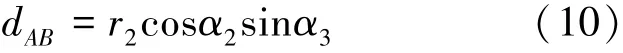
聯立式(9)和(10),可得總的約束式(11)。

(sinα3)2-tanα2sinα3cosα3=(tanα2)2(11)

由式(11)可見,傾角a3和a2相關。當給定轉角a2,角度a3也就確定。因此,大腿-髖關節機構是單約束完整系統。進一步求解公式(11),可得轉角a3的計算公式(12)。

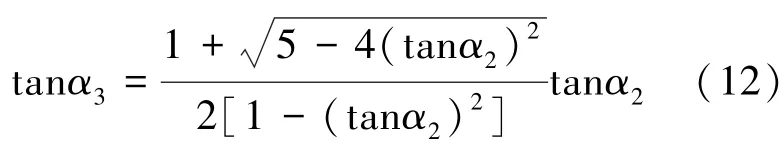
由式(12)可見,分母項不能為零,求得轉角a2變化范圍為0～45°。通常,機構設計任務書都給定大腿擺桿的運動范圍極限角度ad。因此,轉角a2和極限值ad之間存有一定約束關系。由圖7中的線段之間幾何關系,可得到極限角度ad的表達式,如式(13)所示：

綜上,當給定設計參數r2和ad,按照圖8計算流程圖可得大腿-髖關節機構的運動方程。

3.4 仿真算例

進行髖關節轉動角計算仿真時,通常轉角θ1是自由轉動變量,與機構尺寸無關。為計算方便,本算例令轉角θ1=α3-α2。主要考察轉角θ2和θ3的變化情況。 由圖6和圖7可見,θ3=-θ,θ2=-φ。由于上述各公式均為解析表達式,得到結果如圖9和圖10所示。 其中,令r2=226 mm,ad=88°。

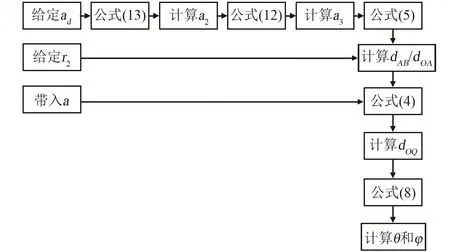
圖8 計算流程Fig.8 Calculation process

由圖可見,這兩個運動角度曲線是連續的、有界的,符合下肢運動的范圍要求和實際步態變化。因此,本文提出的耦合機構模型是合理的,運動分析方程是正確的。

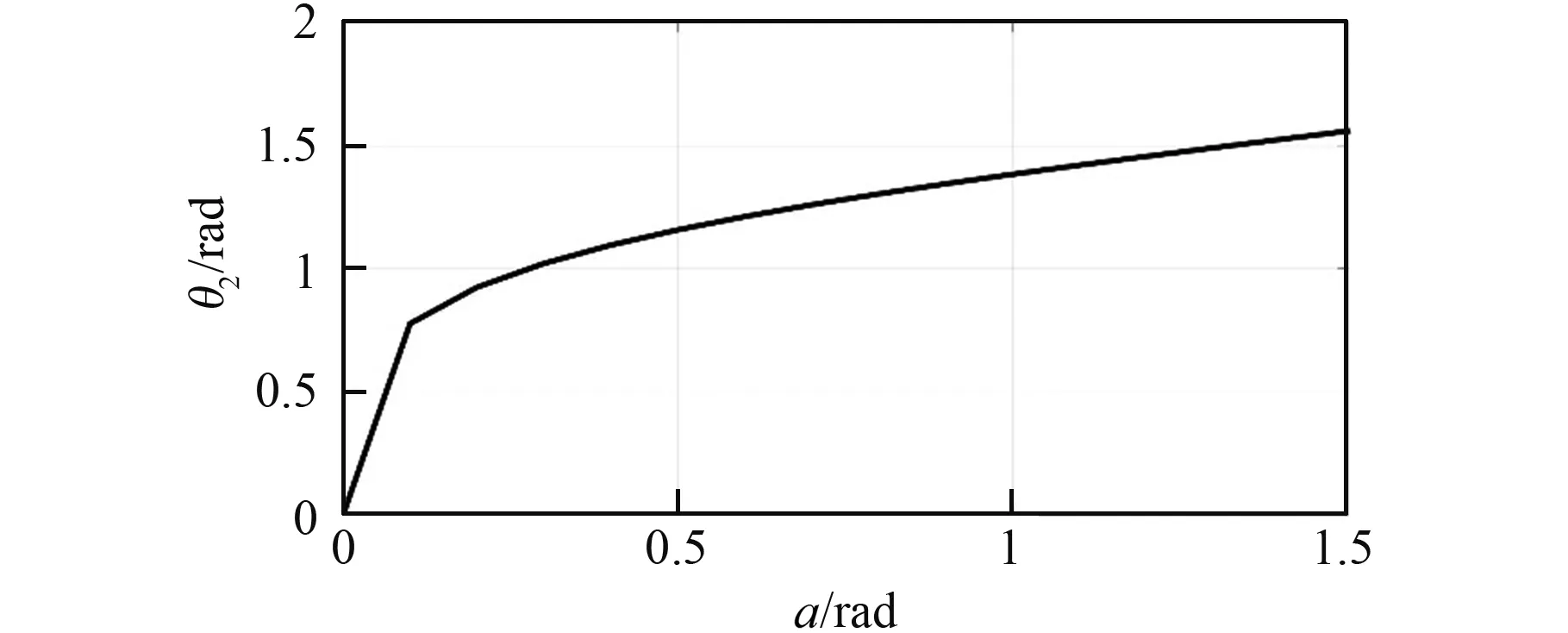
圖9 轉角θ2的變化曲線Fig.9 Curve of rotation angle θ2

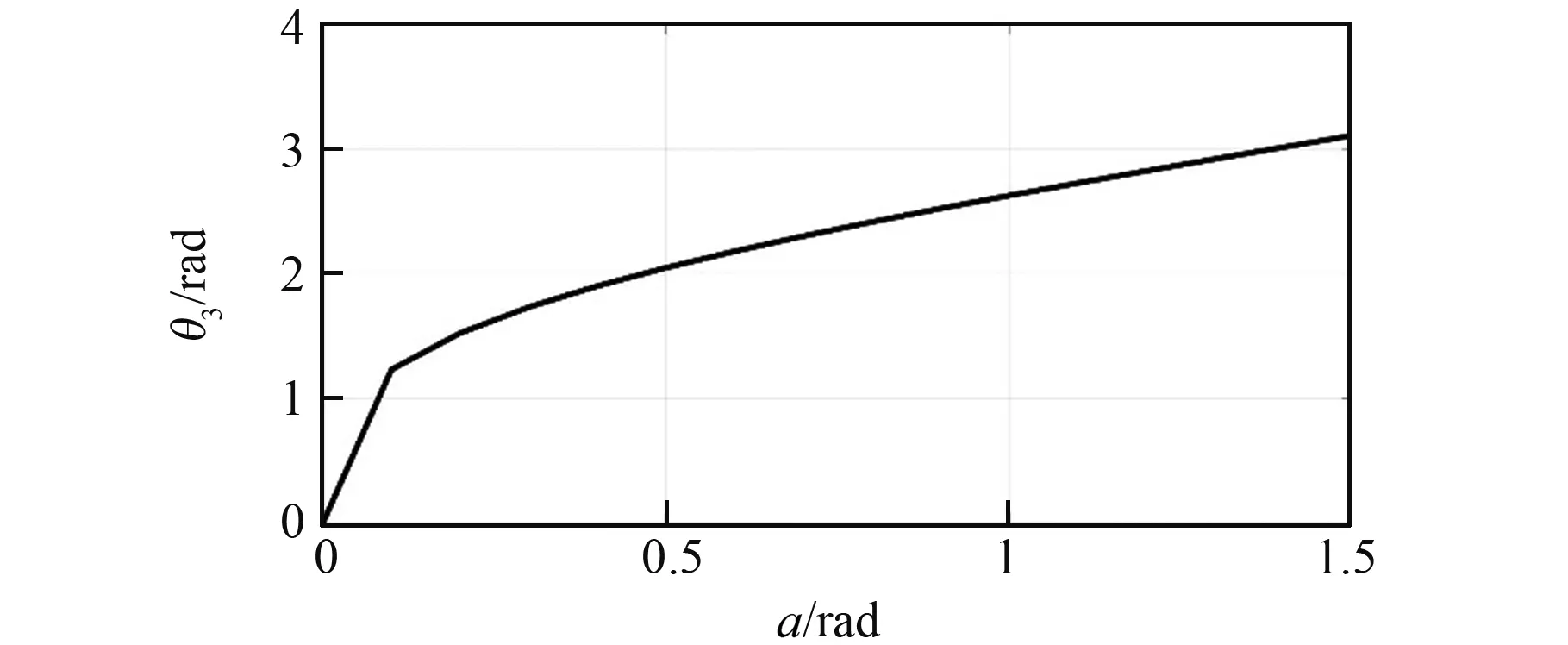
圖10 轉角θ3的變化曲線Fig.10 Curve of rotation angle θ3

4 結論

1)從機構組成原理來講,大腿-髖關節耦合機構是一種串聯混合機構,且與人體大腿具有相同的自由度。

2)大腿-髖關節耦合模型有3個約束條件：3自由度約束、固定約束和正交約束。在上述約束條件下,大腿-耦合機構具有明確的機構構型和運動形式。

3)通過矢量表達方法所建立的機構運動方程與實際人體大腿的運動形式相一致。

4)大腿-髖關節耦合機構是一種參數化模型,可用于不同設計參數的髖關節運動分析,這為航天服硬質髖關節設計提供了一種較為通用的運動分析工具。