空間通信中的一種滑動窗口BATS碼傳輸方案研究

曾 柯,劉曉東,卓永寧*,呂夢昭,王 思

(1.電子科技大學通信抗干擾技術重點實驗室,成都611731；2.空軍裝備部,北京100032；3.上海航天技術研究院北京研發中心,北京100048)

1 引言

在人類空間探索中,空間通信數據傳輸業務對傳輸的可靠性和時效性有很高的要求,例如在載人航天、衛星對地探測、航天器著陸和對接等任務中,艙室監控視頻、航天員身體狀態、科學探測數據、控制指令等數據可靠和及時的傳輸必須得到保證,而空間環境下傳輸鏈路的長時延、高誤碼率、低帶寬、多級中繼使得傳統上依靠反饋確認實現的可靠傳輸性能大為降低,傳輸及時性也由于多級中繼受到很大限制,需要在編碼和通信協議上提出新的方案。

BATS碼(分批稀疏碼,Batched Sparse Code,BATS)[1-2]是近幾年提出的一種結合了噴泉碼和網絡編碼優點的新型編碼技術,既有噴泉碼無需反饋、適合單向長延時信道的特點,又有網絡編碼的優點,能夠在中繼節點進行直接編碼,特別適合空間(深空)通信中長延時、多中繼、高丟包率的鏈路特點[2]。與之相比,噴泉碼在中繼節點上進行譯碼后再重新編碼,或中繼節點直接轉發,同時在源節點上采用更多的編碼冗余以抵抗多級鏈路的累積丟包,這些都會降低編碼效率,增大處理和傳輸延時。已進行的地面視頻傳輸實驗證明,多級鏈路中的有限長BATS碼比有限長噴泉碼有更好的傳輸流暢性、可靠性[2-3]。

BATS碼雖然在多中繼環境表現出一些優越的性能,但其研究和應用尚處于初級階段,許多應用還主要針對地面高速數據傳輸[4-5],如何針對應用環境進一步優化尚未見深入的研究。另一方面,空間通信既要求較高可靠性,又要求較高傳輸時效性。已有針對無反饋可靠傳輸的研究[6-8],通常利用數據包的冗余傳輸保證可靠性,但實際上仍然無法保證數據的快速及時傳輸。基于此,本文提出一種BATS碼的滑動窗口傳輸方案,相對于一般的窗口連續重疊滑動方式[7-9],利用BATS碼中小度值Batch具有更高可解概率的特點,以多個小度值Batch對滑動窗口的非重疊區域進行編碼傳輸,同時將滑動步長改為不等步長,實現對窗口滑動前后的重疊區域和非重疊區域數據的均衡保護,從而較好地解決空間通信中可靠傳輸與及時傳輸這一對矛盾,實現較高效率的傳輸。

2 BATS碼基本原理

2.1 BATS碼的編碼方法

BATS碼編解碼中具有分批處理(Batch)的概念。假設待編碼的數據包數量為K,集合B=(1,…,K)表示所有數據包的集合,將該集合劃分為n個子集(可有重疊),子集Bi?B,i=1,…,n。 每一個集合Bi經編碼后得到M個編碼數據包,稱為一個分批(Batch)。編碼后得到的n個Batch表示為X1,X2,…,Xn, 每個 Batch 可表示為式(1)[1]：

其中,令di=|Bi|,即Bi中包含di個原始數據包,稱di是BatchXi的度。di(i=1,…,n) 是獨立同分布的隨機變量,稱其分布Ψ=(Ψ1,…,Ψk)為度分布(Degree distribution),即Pr{di=k}=Ψk。Gi是di×M的隨機矩陣,稱為生成矩陣。理論上,編碼后的Batch數目n可以是無限的。BATS碼的編碼和傳輸過程如圖1所示,生成矩陣Gi處的虛框表示生成的Batch,虛框內的實心方塊表示每個Batch內的M個編碼數據包。

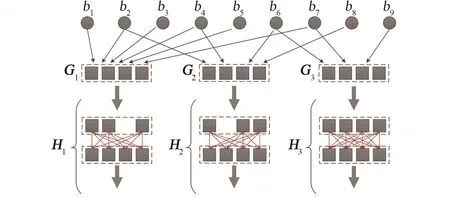
圖1 BATS碼的編碼和傳輸過程示意圖Fig.1 The encoding and transmission process of BATS code

傳輸數據包時,由于存在丟包現象,每個Batch到達中間節點的數據包數量可能少于M。中間節點對屬于同一Batch的數據包使用網絡編碼(文獻[1]中使用線性隨機網絡編碼),重新產生M個數據包,并轉發給下一節點。到達接收端的第i個Batch可表示為式(2)。

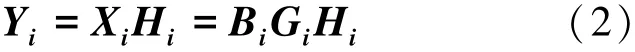
式中,Hi是一個M行的隨機矩陣,稱為傳輸矩陣。Hi的列數等于第i個Batch到達接收端的數據包的數量。對于不同的分組,該值不一定相同,但一定小于等于M。

2.2 BATS碼的解碼方法

BATS碼常用的解碼方法是置信傳輸(Belief Propagation,BP)解碼。經過編碼和傳輸之后,接收端收到的信息是BatchYi(i=1,…,n),數據包頭信息中包含的傳輸矩陣H,以及通過收發端協商得到的生成矩陣G。 于是,解碼器可使用的解碼信息是 (Yi,GiHi)(i=1,…,n),解碼即相當于求解線性方程組。對于一個 Batch,當秩 rank(GH)等于這個Batch包含的原始數據包數目(即Batch的度)時,該Batch可解,對應的原始數據包稱為可解的數據包。顯然,當一個Batch中包含的原始信息包的數量較少時,傳輸中的丟包對其影響較小,該Batch有更高的可解概率。

BP解碼包含多次迭代,每次迭代時,選擇一個可解數據包,將其帶入與之關聯且不可解的Batch中。帶入后,該數據包被標記已解,此時不可解的Batch可能會變得可解,然后進入下一次迭代。當沒有任何可解的數據包時,解碼結束。

當BP解碼無法進行下去時,還可通過高斯消去法對剩余的Batch進行解碼,即BP-GE算法[4]。

2.3 傳輸性能與Batch度分布的設計

實際應用中,源信息包和BATS編碼包數量有限,因此是有限長BATS碼。我們希望傳輸盡量少的編碼包就能完全恢復原始信息包。與噴泉碼類似,有限長BATS碼是否可譯以及其傳輸效率與Batch的度分布有很大關系。由于Batch在傳輸中出現隨機的丟包,對應到傳輸矩陣H中是隨機的列矢量丟失,而BATS碼是否可譯取決于矩陣GH的秩,因此好的度分布需要基于傳輸矩陣H的秩的分布情況進行設計。令：

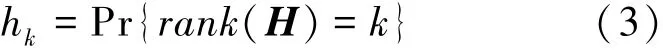
稱矢量h=[h1,h2,…,hM]為H的秩分布。秩分布反應出數據包從源節點到目的節點之間鏈路的隨機丟包情況。

發送端Batch度分布在設計時,直接獲取適應信道丟包情況的最優Batch度分布是一個較為困難的問題。文獻[1]、[4]證明,最優度分布可通過漸進優化的方法來得到。首先通過求解一個有限長BATS碼的可達編碼率的線性最優化問題,來獲得一個初始的度分布：

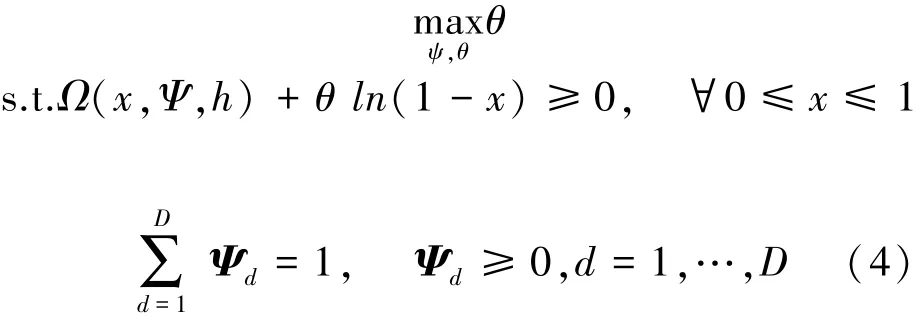
式(4)中可達編碼率θ=K/n,為優化的目標函數,n為Batch的數量。Ψ為Batch的度分布,D是最大度值,x是取值在[0,1]間的離散參數。函數Ω(x,Ψ,h)由下式給定：

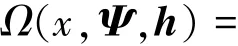
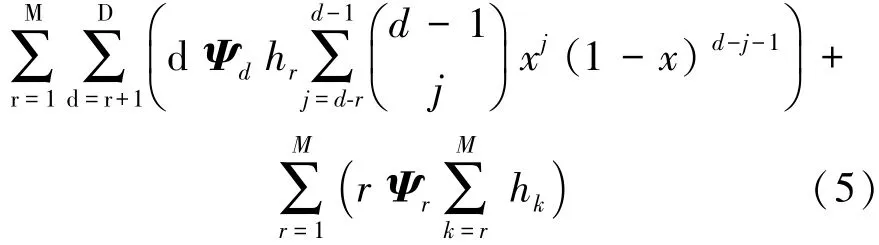
由式(5)獲得的初始度分布基礎上,通過迭代貪心算法[4],獲得性能更好的度分布值,貪心算法的具體步驟為：

1)找到一個初始度分布Ψ(0)；

2)找到一個或多個可能好于初始度分布的新度分布Ψ(1)；

3)計算譯碼失敗概率,選擇性能最好的度分布,并重復步驟2、3。

文獻[4]中尋找新的度分布使用下述擾動方法：

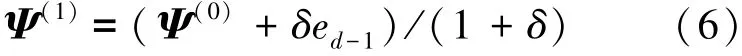
其中δ是一個很小的實數值,ed-1是一個某一元素為1、其他元素為0的d維矢量。

3 滑動窗口BATS碼傳輸方案

3.1 傳統滑動窗口傳輸方案分析

滑動窗口是一種在流媒體傳輸中用于提高傳輸可靠性的方法,在噴泉碼、RS糾刪碼(Reed Solomon,RS碼)傳輸中獲得了廣泛的研究[7-9]。其基本方法如圖2所示。

將需要傳輸的數據分為長度為L的分段,稱為一個窗口。對窗口W1內的數據進行編碼傳輸,然后將窗口的起點向后移動S個符號,稱為滑動S步長,然后將該起點以后的新窗口W2內的L個符號進行編碼傳輸。圖2中的P為前后兩個窗口的重疊部分。

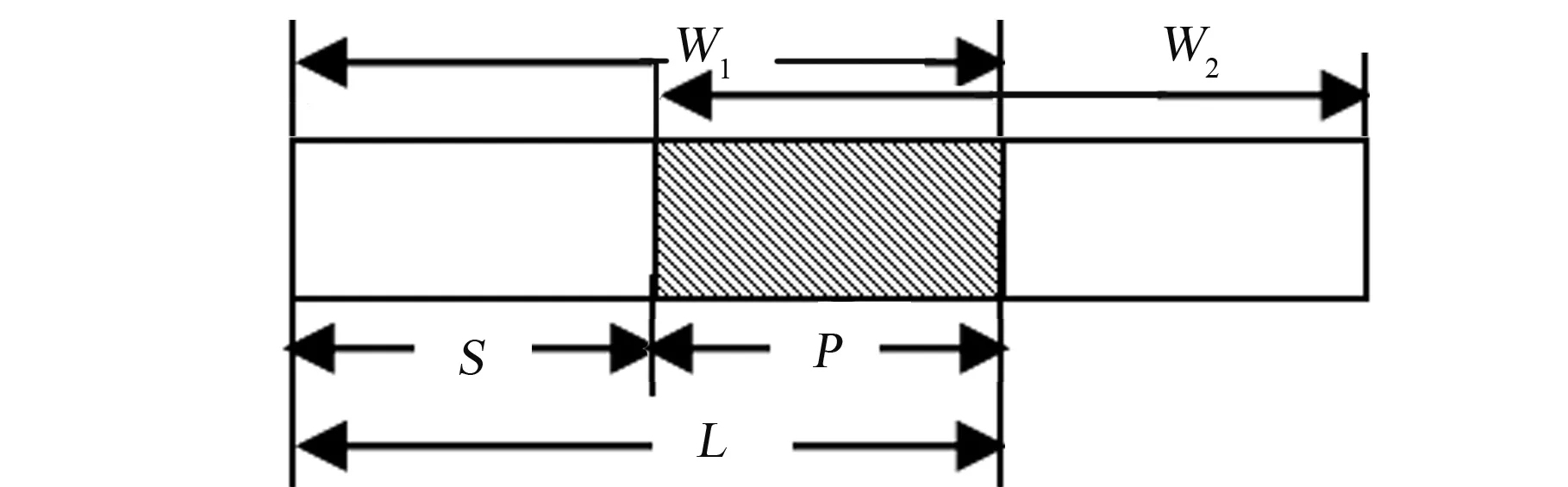
圖2 基本滑動窗口傳輸Fig.2 The basic sliding window transmission

上述窗口滑動方法是一種重疊滑動,以數據的冗余傳輸實現對窗口滑動前后重疊部分的增強保護,這部分數據的傳輸可靠性高于不重疊部分。如果窗口連續滑動,則將出現更多的數據重疊,其中對不同重疊程度的數據保護程度也不同。例如當滑動步長S小于重疊部分P的長度時,如果連續重疊滑動,則可能出現部分數據有三重重疊,導致部分數據被過度保護,而其他部分保護的程度較低或沒有保護,如圖3所示。如果對所有數據連續采用這種方式進行滑動,將會導致較多的不必要數據冗余,同時也會造成窗口滑動太慢,數據傳輸耗時過長。

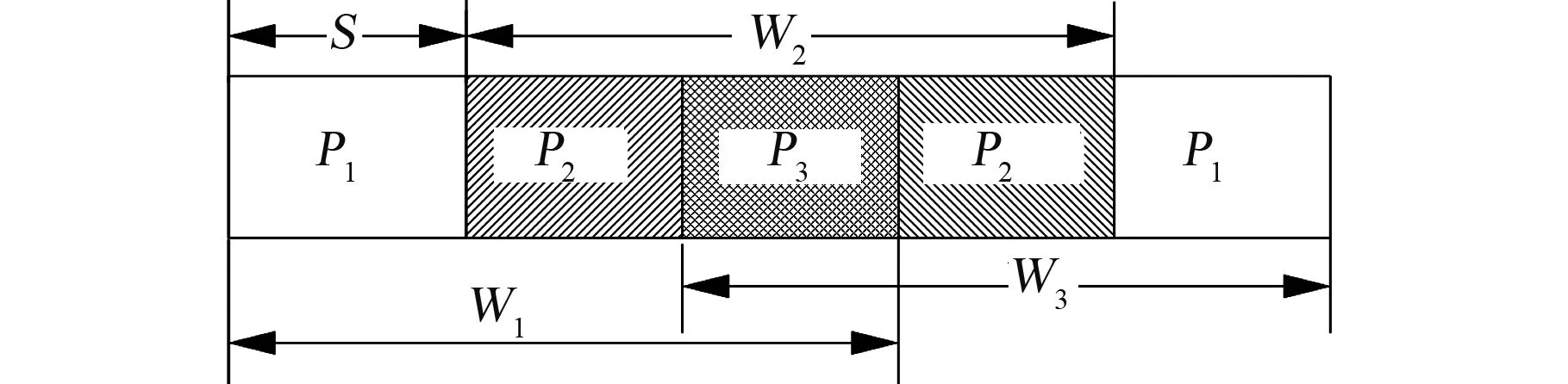
圖3 窗口連續滑動造成的不同重疊區域P2：二重重疊,P3：三重重疊Fig.3 The overlapping field of a data section caused by consecutive sliding window transmission P2： Double overlapped part P3：Triple overlapped part

3.2 均衡保護的滑動窗口BATS碼傳輸方案

BATS碼是將數據分批編碼,有限長BATS碼的編碼長度固定,不同分批的BATS碼可以進行聯合譯碼。根據前面BATS碼編譯碼過程分析,可知BATS碼中度值較小的Batch具有更高的可解概率。基于此特點,可以實現一種均衡保護滑動窗口傳輸中重疊與非重疊數據的傳輸方案。流程如下：

1)發送方首先根據鏈路情況得到秩分布,并根據秩分布得到一個期望秩rankexpt,設定每個Batch的尺寸M大于rankexpt；

2)發送方建立一個長度為L的發送窗口,根據窗口長度及秩分布,通過求解式(1)中的漸進優化問題得到Batch的度分布、編碼率和每個窗口需發送的編碼包數量；

3)每次發送時,根據Batch度分布隨機選取一個度值Degree。如果Degree的數值小于rankexpt,則在窗口未重疊區域中順序選擇Degree個數據,進行Batch編碼并發送；如果Degree值大于rankexpt,則在當前整個窗口中隨機選擇Degree個數據形成Batch編碼并發送。當本窗口中所有編碼數據包數量達到第2步中確定的編碼包數量時,本窗口中的數據停止發送；

4)將窗口進行滑動：當本窗口數據發送完畢后,如果本窗口還未與其他窗口發生重疊,則只順序滑動所有小度值Batch的度值之和的長度；如果本窗口與前一窗口已發生重疊(即是一個已經滑動的窗口),則前移一個完整的窗口長度,從本窗口結束位置后重新選擇L個新數據作為新的窗口,開始第3、4步的發送流程,直至數據發送完畢。

上述數據發送過程見圖4。圖中第一個窗口為W1,該窗口中的數據發送時,如果隨機選擇的度值小于rankexpt,則順序選擇窗口中前面的Degree個數據進行編碼發送,如果超過或等于rankexpt,則在整個窗口內隨機選擇Degree個數據進行編碼發送,這一過程重復直到所發送的編碼數據包數量達到第2步確定的編碼包數量；隨后窗口滑動所有小度值之和的步長S1,成為窗口W2。在W2中的數據發送時,當選擇的度值小于rankexpt值時,從W2與W1重疊的部分P1之后的數據中順序選擇Degree個數進行編碼發送；當選擇的Degree值大于rankexpt時,則在整個W2窗口中隨機選擇數據進行編碼發送,直到整個W2中的編碼數據包數量達到要求。然后,選擇新的數據形成新窗口W3,重復上述過程。上述過程中,兩個窗口重疊的部分P1、P3得到冗余發送的保護,增大了譯碼成功的概率；未被重疊窗口覆蓋的數據S1、S2、S3、S4,由于采用小度值進行編碼,也具有較高的譯碼成功概率,因此,所有編碼數據都得到了較高的譯碼成功率,從而提高了數據傳輸的可靠性。

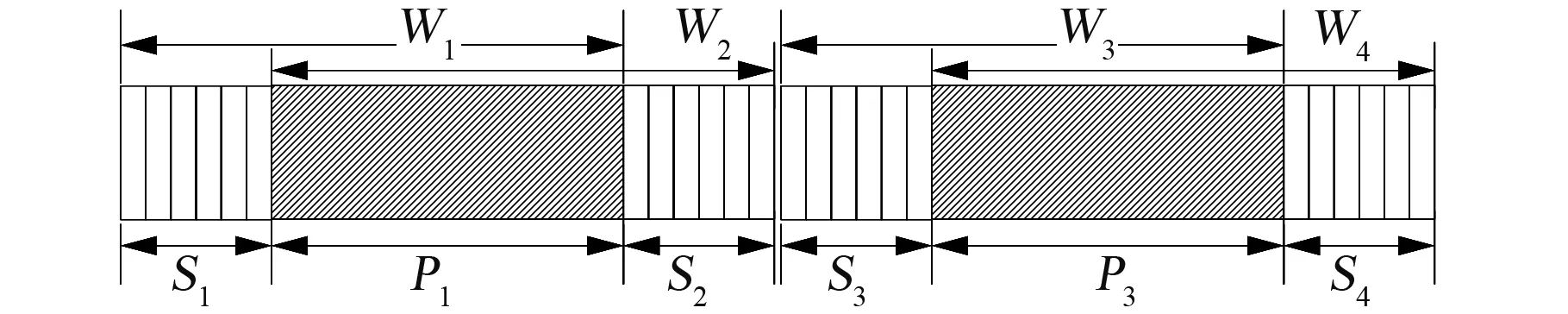
圖4 均衡保護的滑動窗口傳輸方式Fig.4 Sliding window transmission with balanced protection mode

3.3 Batch度分布優化算法

分析上述策略,數據包的發送效率和發送速度取決于整體Batch度分布。假設數據包總數為1024,窗口長度wnd_len為256,通信鏈路為互相獨立的多跳鏈路,鏈路長度為2,每一跳的丟包率p為0.2,取M=16,鏈路拓撲如圖5所示。

通過2項式分布擬合,得到的秩分布如圖6所示。其中秩期望值rankexpt的值為12.87。基于上述秩分布,通過求解前述式(4)關于編碼率的優化問題得到的度分布如圖7所示。

根據上述策略,每次選取的度值小于rankexpt的概率較小,最后將會導致窗口移動速率過慢。這種情況可能在優化問題式(4)的求解中經常出現。因此,本文提出一種基于貪心算法的窗口滑動度分布生成算法,用以提高小度值的選擇概率。算法描述如下：

圖5 中繼鏈路拓撲Fig.5 The topology of multi-relay transmission

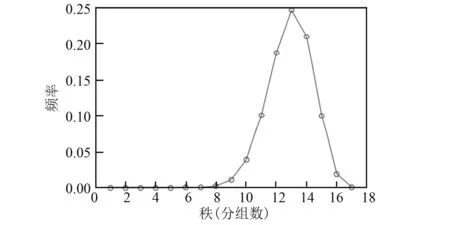
圖6 矩陣GH的秩分布Fig.6 The rank distribution of GH

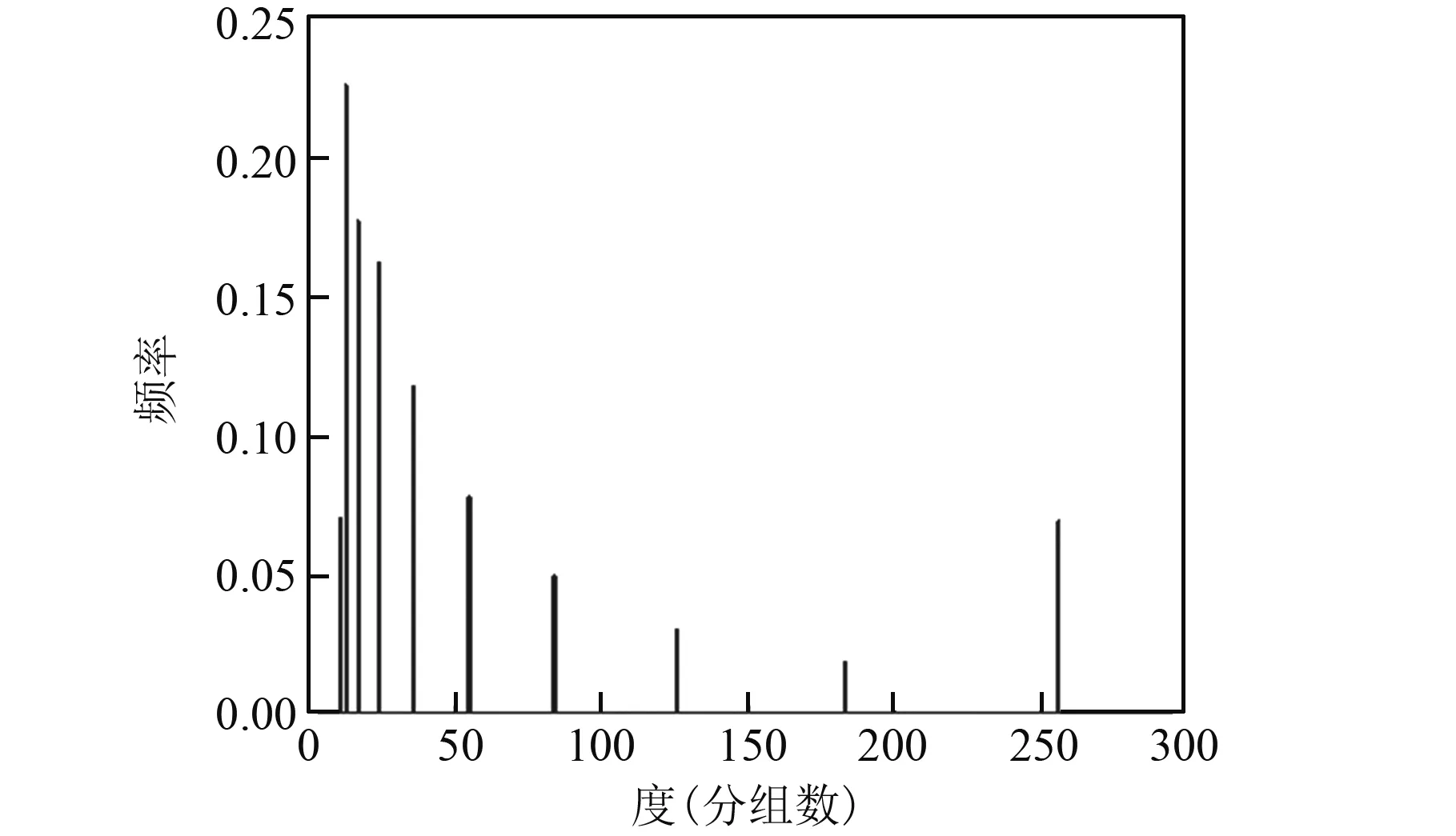
圖7 求解(4)式優化問題得到的BATS碼分批Batch的度分布Fig.7 The distribution of Batch degree obtained by solving the optimization problem of formula(4)

loop_times//定義迭代次數adjust_value//定義每次調整的度分布值fori=1：loop_times//循環loop_times次計算給定度下的譯碼失敗概率；

If本次譯碼失敗概率在可接受范圍內隨機從度分布中挑一個大于rankexpt的度數減去adjust_value；

再隨機從度分布中挑一個小于rankexpt的度數加上adjust_value；

else

break；

end if

end for

通過這種方式生成的滑窗度分布見圖8。由圖8可見,小度值(小于12)的概率大大提高了,這將有利于提高數據整體的發送速度,提高數據發送效率。

圖8 經過調整的適于滑動傳輸的BATS碼分批Batch的度分布Fig.8 Adjusted distribution of Batch degree suitable for sliding window transmission

4 仿真分析

仿真具體場景為三點兩跳鏈路,每一跳的丟包率p在效率仿真中設為0.2,在可靠性仿真中設為可變,源數據包總數為1024,鏈路無反饋。為了比較有無滑窗和不同滑窗方式的傳輸性能,對比以下4種策略：

1)編碼方式采用經典噴泉碼,即LT碼(Luby Transform,LT碼),采用有限碼長,譯碼方式為高斯消元GE譯碼算法,對原始數據順序分段編碼發送(即分段之間無重疊),分段長度256,每分段編碼包長度480。本策略模擬無滑窗的LT噴泉碼傳輸；

2)編碼方式為BATS碼,譯碼方式采用BP譯碼算法,有限域大小為Fq=256,采用對原始數據順序分段編碼發送,分段之間無重疊,Batch尺寸為M=16,分段長度為256,每分段編碼包長度為480,其Batch度分布為圖7所示的度分布。本策略模擬無滑窗的BATS碼傳輸；

3)編碼方式為BATS碼,譯碼方式采用BP譯碼算法,有限域大小為Fq=256,發送策略采用順序重疊滑動方式(即圖3中的發送方式),Batch尺寸為M=16,編碼包的窗口長度為480。本策略模擬傳統的連續重疊滑窗BATS碼傳輸；

4)編碼方式為BATS碼,譯碼方式采用BP譯碼算法,有限域大小為Fq=256,發送策略采用本文提出的均衡滑動方式,Batch尺寸為M=16,每窗口中源碼包數量為256,每窗口發送編碼包數量480,采用圖8所示的度分布。本策略模擬本文提出的均衡保護滑窗BATS碼傳輸。

圖9是數據成功恢復比例隨發送數據包數量的變化情況。從圖9可以看到,在成功恢復率方面,滑動窗口方式的成功恢復率均高于無滑窗方式。無滑窗方式時,當發送相同數量的數據包時,BATS碼的成功恢復率高于LT碼,當達到100%恢復率時,LT碼約需發送2500個數據包,而BATS碼需要發送約2300個數據包；采用滑動窗口的兩種BATS碼方式中,均衡保護滑窗的成功恢復率都高于連續滑窗的成功恢復率,且隨著發送的數據包數量增多,這種優勢越來越大。當數據包達到100%恢復率時,連續滑動BATS碼方式約需傳送1980個數據包,而均衡滑動BATS碼約需發送1750個數據包。

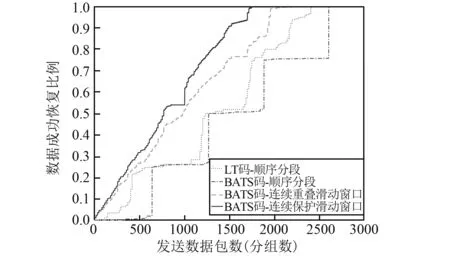
圖9 不同傳輸策略下的數據成功恢復比例Fig.9 The data recover rate of different transmission schemes

圖10是實時發送效率的變化情況,此處實時發送效率定義為：實時發送效率=正確接收的數據比特數/發送編碼比特數。從圖10可以看到,無滑窗方式由于成功解碼的過程大部分集中在分段的末尾,因此實時能力波動較大,且一直在一個較低的水平；連續重疊滑窗方式由于滑動窗口的特性,保證了數據的實時傳輸性能,將實時性能維持在一個平衡的狀態,但其傳輸效率指標并不是很高；均衡保護滑窗方式相對無滑窗方式以及連續重疊滑窗方式來說,不僅結合了滑動窗口的特性保證了實時性能的穩定,同時利用雙段窗的特性提升了數據傳輸效率,將實時傳輸效率一直維持在一個相對較高的水平,這說明本文的發送策略有較高的效率,從而也具有較高的時效性。從圖10也可以看到,在穩定狀態下,均衡保護滑窗方式的效率約為60%,相對于連續重疊滑窗方式的約50%,提高了約20%。

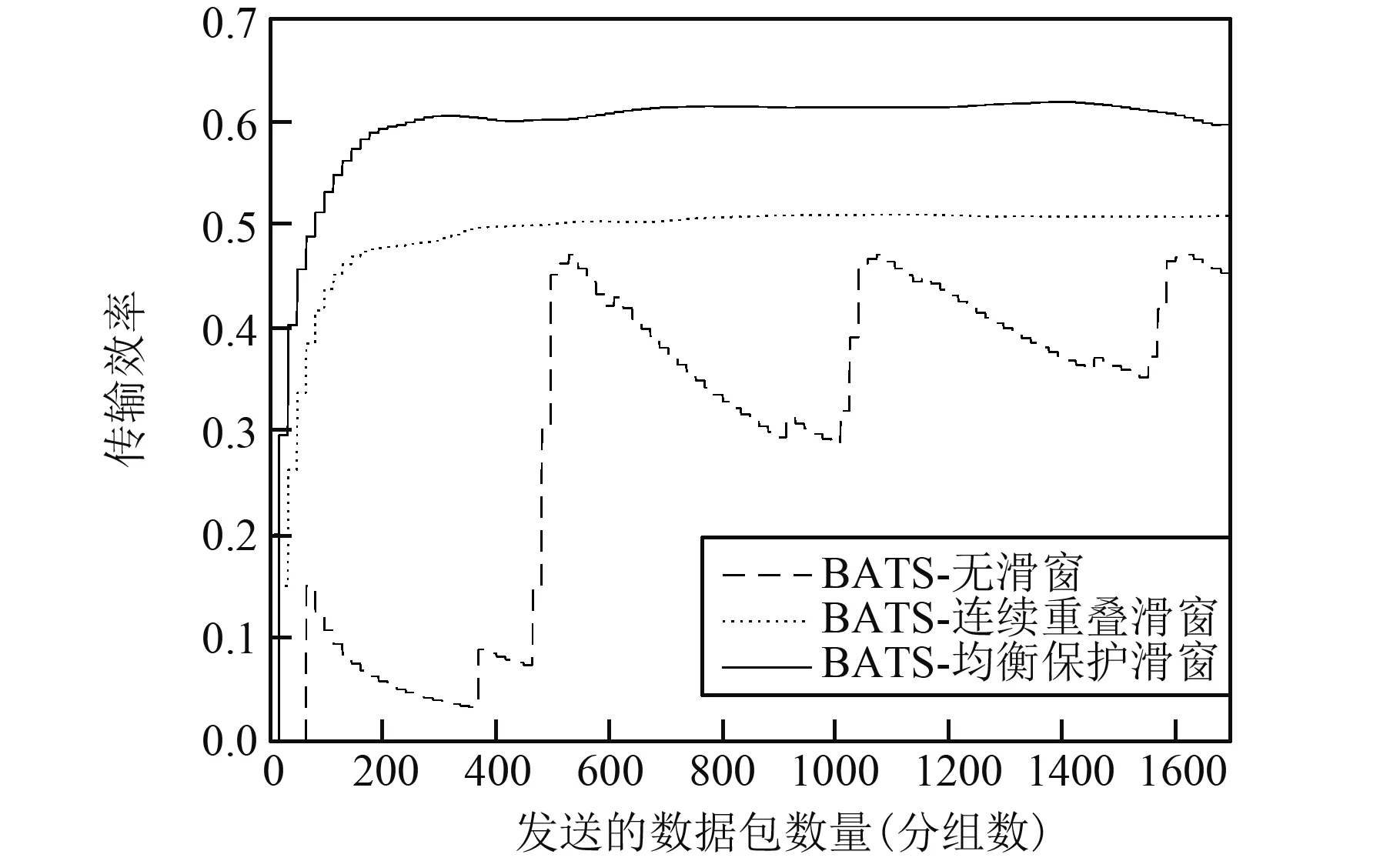
圖10 不同滑動方式下的實時發送效率Fig.10 The real time transmission efficiency of different sliding window modes

圖11是在不同的信道丟包率下,發送固定數據包數量情況下的數據恢復成功率。圖中發送的編碼數據包數量固定為2700。從圖11可見,不同傳輸方案在不同丟包率情況下的成功恢復率也不同,該指標可反映各方案的傳輸可靠性。圖中當鏈路丟包率低于0.3時,各傳輸方案都可以成功恢復數據,但當丟包率達到0.4以上時,無滑窗方式的成功恢復率很快下降至0,而滑窗方式還可以維持在較高水平。其中連續滑窗方式的成功恢復率水平略高于均衡保護方式,這表明均衡保護滑窗方式的可靠性雖低于連續重疊滑窗方式,但仍然維持在較高的水平,可適用于最大丟包率達到0.4的情況。

圖11 不同丟包率下的數據成功恢復率Fig.11 The data recover rate of different packet loss rates

5 結論

本文針對空間通信中鏈路傳輸時延大、丟包率高、中繼傳輸多的問題,利用BAST碼的良好中繼傳輸特性,提出了一種兼顧傳輸效率和可靠性的傳輸方法,其主要特點是：

1)充分利用BAST碼分批處理的概念,利用滑動窗口進行具有一定冗余的傳輸,提高了在高丟包情況下的數據恢復成功率,提高了可靠性；

2)傳輸中利用了BAST碼小度值編碼包的高恢復率,合理安排了小度值編碼包在滑動窗口中的位置,使其減少冗余傳輸次數,同時使高度值的編碼包得到更多的傳輸機會,從而控制了數據的總的冗余傳輸次數,有利于提高傳輸的效率；

3)通過上述方法,實現了在空間通信中高丟包率情況下,既具有較高的傳輸可靠性,又具有較高的傳輸效率,打破了傳統上依靠冗余傳輸來提高可靠性與提高效率之間難以兼顧的困境。通過仿真實驗表明,本方案在維持與傳統的連續重疊滑窗相近的可靠性同時,傳輸效率提高約20%。