基于IAPF算法的無人艇動態編隊自主路徑規劃*

劉夢佳 馮 輝 徐海祥

(武漢理工大學交通學院1) 武漢 430063) (高性能船舶技術教育部重點實驗室2) 武漢 430063)

0 引 言

多無人艇編隊(unmanned surface vehicle formation,USV Formation)系統已成為無人艇領域的研究熱點.相較于單艇作業，無人艇編隊具有信息處理能力強、負載能力高、覆蓋范圍大等優勢，在應急救援、水質采樣、氣象監測、信息偵查等領域有廣闊的應用前景[1].國內外對編隊控制進行廣泛的研究，編隊模型控制的主要方法有領航者-跟隨者(leader-follower,L-F)法、基于行為(behavior-based)法、虛擬領航(virtual leader)法和基于圖論法等[2]，每種方法都有著優缺點，因此，隊形控制目前還沒有形成統一有效的算法.

L-F法因其簡單性和良好的擴展性成為無人艇編隊控制領域的研究熱點[3-4]，編隊路徑規劃見圖1.

圖1 編隊路徑規劃示意圖

對領航艇進行路徑規劃，根據領航艇的位置和艏向信息計算出跟隨艇的位置信息，從而完成整體編隊系統的路徑規劃.Liu等[5-6]采用快速行進法，采用L-F編隊控制，解決了USV編隊路徑規劃問題.張瑞雷[7]提出一種多機器人動態協調控制算法．建立跟隨機器人對虛擬機器人軌跡跟蹤系統模型.Ali等[8]采用勢場法對L-F編隊系統進行了機器人路徑規劃實驗，驗證了勢場法的可行性.吳垠[9]采用L-F法對多智能體編隊控制問題進行了研究，設計了一種能夠實現其穩定編隊的迭代學習控制算法.

人工勢場法(artificial potential field,APF)將障礙物和目標假設為相互作用的靜電荷進行建模，從而在無人艇周圍形成一個潛在的勢場.人工勢場法的計算簡單和實時性好，但主要缺點是尤其是障礙物的坐標未知情況下，APF算法可能存極小值即在局部存在死鎖的位置，阻礙無人艇到達目標.為了克服這些局限性，Adeli等[10]將工作空間離散化為矩形網格，Zhang[11]針對凸障礙或凹障礙環境提出了一種改進的隨墻方法，葉錢波[12]利用松弛變量將約束優化問題轉化為無約束優化問題.

為適用于無人艇的動態運動，本文在對已有的方法進行深入分析的基礎上，對傳統的人工勢場法改進得到IAPF(Improved APF)算法，并且在國內外研究的基礎上，本文針對無人艇編隊通過狹窄水域的問題，提出自適應編隊控制策略，自適應調整隊形.

1 無人艇編隊模型

1.1 單艇運動模型

對于無人艇的路徑規劃問題，只研究三個自由度的平面運動，即縱蕩、橫蕩和首搖運動.單艇三自由度運動模型見圖2.

圖2 單艇三自由度運動模型ψ-首向角；u-船舶縱向線速度；v-橫向運動線速度；r-角速度；V-無人艇運動速度；G-重心.

1.2 編隊運動模型

采用L-F結構作為編隊運動控制模型，無人艇編隊運動模型示意圖見圖3.采用L-F編隊結構進行計算時需要參考至少三條艇之間的相對距離和相對方位信息.假設以三條艇的編隊控制為例.三條艇之間的關系為，一條領航艇和兩條跟隨艇，這種方法只需要對兩條跟隨艇到領航艇之間的期望和實際距離信息ld和l進行控制，保持艇體間相對距離不變就可以達到控制編隊隊形的目的.

圖3 編隊運動模型L1，L2-跟隨艇USV1和跟隨艇USV2與領航艇USVL之間的相對距離；ψ1，ψ2-兩跟隨艇的首向角

只要將領航艇與跟隨艇之間的實際相對距離L與期望相對距離LR之差ΔL、實際相對角度φ與期望角度φR之差Δφ保持在允許的誤差范圍內即可達到隊形控制的目的，滿足約束條件為

ΔL=‖L-LR‖≤δL

(1)

Δφ=‖φ-φR‖≤δφ

(2)

標準的L-F編隊控制結構的隊形穩定性高，但不利于動態調整編隊中跟隨艇的位置，所以本文提出虛擬跟隨者的編隊控制結構，具體是設置一艘虛擬跟隨艇USVV，與另一艘跟隨艇USV2保持相同的期望相對距離和期望角度，跟隨艇USV1的位置和角度可以根據虛擬跟隨艇的位置推算出.虛擬跟隨者的L-F具體示意圖見圖4.

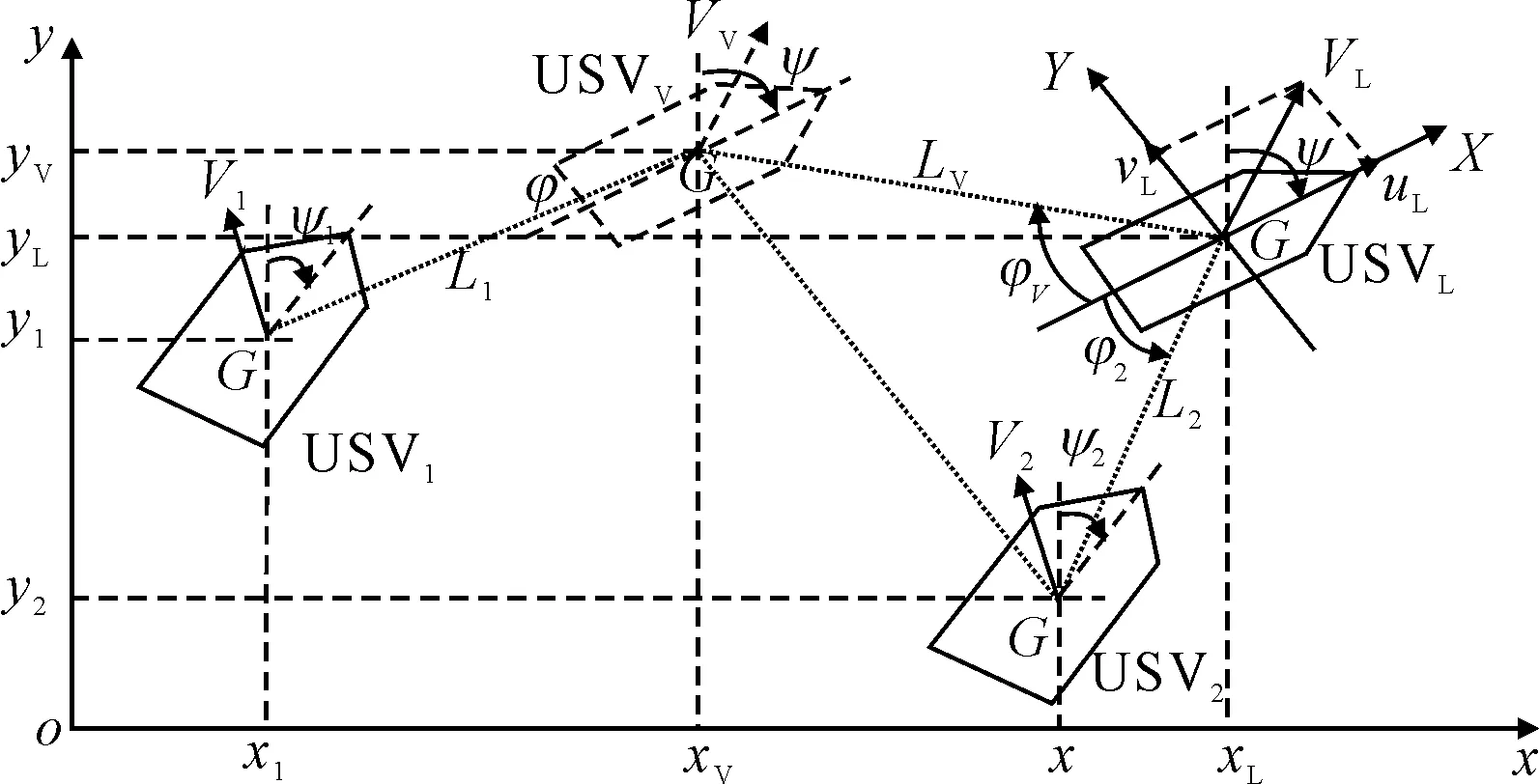
圖4 虛擬跟隨者-編隊運動模型

由圖4可知，無人艇USV1，USV2是USVL的跟隨無人艇，USVV是無人艇USV1需要跟隨的虛擬無人艇，與USVL保持期望距離LV和期望角度φV，根據USVL的位置和首向角即可得到USVV的位置和首向角.

為達到所需的編隊控制結構，假設φ1=0°，各跟隨艇的位置計算為

φV=φ2

(3)

VV=VL

(4)

xV=xL-LVsin (ψ+φV)

(5)

yV=yL+LVcos (ψ+φV)

(6)

x2=xL-L2sin (ψ-φ2)

(7)

y2=yL-L2cos (ψ-φ2)

(8)

x1=xV-L1sinψ

(9)

y1=yV-L1cosψ

(10)

2 自適應編隊控制策略

2.1 自適應調整跟隨角

在無人艇編隊進行自主避障時，需保證跟隨艇USV1和USV2避免碰撞到障礙物，對兩艇跟隨角進行自適應調整策略，當兩跟隨艇分別距左、右障礙物的距離小于安全距離時，根據其可通航水域寬度自適應調整兩艇跟隨角以避開障礙物，具體計算為

(11)

(12)

式中：φ1為跟隨艇USV1跟隨角；φ2為跟隨艇USV2跟隨角；B1為跟隨艇USV1距左側障礙物的距離；B2為跟隨艇USV2距右側障礙物的距離.

2.2 自適應隊形控制

在自適應調整跟隨角的基礎上，針對通航水域較窄的情況提出自適應隊形控制，具體策略為將無人艇編隊看作一個整體，在寬闊水域，按照前文提出的虛擬跟隨艇L-F編隊控制策略進行航行，在狹窄水域，根據水域寬度自適應調整編隊整體寬度，即自適應調整φ，為

(13)

(14)

式中：B為可通航水域寬度.

當可通航水域寬度只能通過一艘艇時，即φV=φ2=0°，領航艇與跟隨艇保持一字隊形通過狹窄水域，見圖5.

圖5 自適應調整編隊結構示意圖

3 IAPF算法

3.1 基本原理

APF基本思想是在環境中的無人艇，對目標位置構造引力勢場和靜態障礙物周圍構造斥力勢場.引力吸引無人艇朝目標點方向運動，斥力阻止無人艇向障礙物方向運動，在這兩個勢場力共同作用下使無人艇向目標運動.

定義S空間內，無人艇位置r(x1,y1)，目標位置g(x2,y2)，無人艇到靜態障礙物的最近位姿點oi(x3,y3)，環境中目標對無人艇產生的引力場Uatt的吸引力Fatt，靜態障礙物對無人艇產生的斥力場Urep的斥力Frep見圖6.引力場和目標吸引力為

Uatt(ρ(r,g))=ξ‖ρ(r,g)‖m

(15)

Fatt(ρ(r,g))=-Uatt(ρ(r,g))=

mξ‖r(x1,y1)-g(x2,y2)‖m-1ρ(r,g)

(16)

式中：m值為勢場函數曲線的形狀；ξ為目標勢場系數；ρ(r,g)為無人艇與目標物距離函數，ρ(r,g)=‖r(x1,y1)-g(x2,y2)‖；Uatt(ρ(r,g))為Uatt在無人艇位置r(x1,y1)處勢場變化率最大的方向；ρ(r,g)為無人艇到目標的單位矢量.

圖6 二維環境S中無人艇的引力和斥力

靜態障礙物對無人艇產生的斥力場及相對應的斥力為

(17)

Frep(ρ1(r,o))=-Ureps(ρi(r,o))=

(18)

式中：ρ0為障礙物的斥力影響距離，只有在ρ0的范圍之內無人艇才受到障礙物的排斥作用；ρi(r,o)為無人艇與第i個靜態障礙物的最小距離，ρi(r,o)=‖r(x1,y1)-oi(x3,y3)‖；ρi(r,o)是由oi(x3,y3)指向r(x1,y1)的單位向量.

傳統的人工勢場法勢場參數取值不易選取，且生成的路徑容易產生局部極小值，局部震蕩.同時未考慮到動態障礙物的情況.

3.2 改進方法

3.2.1改進引力場

改進后的引力場函數包含了無人艇與目標物的相對位置、相對速度和相對加速度產生的勢場，改進后的引力場計算公式為

Uatt(q,v,a)=αq(ρ(r,g))m+

αv‖v‖n+αa‖a‖p

(19)

式中：αq，αv，αa和m，n，q為比例系數，不同的值表示在引力函數中無人艇和目標點相對位置、速度和加速度信息的權重.由引力場可推得相應的吸引力大小為

Fatt(q,v,a)=-Uatt(q,v,a)=

(20)

Fatt(q)=-?Uatt(q,v,a)/?q=

mαq(ρ(r,g))m-1ρ(r,g)

(21)

Fatt(v)=-?Uatt(q,v,a)/?v=nαv‖v‖n-1v

(22)

Fatt(a)=-?Uatt(q,v,a)/?a=pαa‖a‖p-1a

(23)

勢場引力可表達為

Fatt(q,v,a)=Fattq(q)+Fattv(v)+Fatta(a)

(24)

圖7 無人艇所受勢場引力合力示意圖

3.2.2改進斥力場

(25)

(26)

算法流程見圖8.

4 仿真結果分析

采用的仿真平臺是MATLAB，仿真是基于二值化圖像且不考慮風、浪、流作用下的無人艇編隊路徑規劃，仿真圖像像素大小為500×500，為便于分析仿真結果，表1～2給出了船舶參數和算法參數.

表1 船舶參數

表2 算法參數

為便于對比分析仿真結果，本文首先對傳統的人工勢場法與改進后的人工勢場法進行算法的性能對比；然后對比應用于無人艇編隊的效果，對比虛擬跟隨者L-F與標準的L-F效果；最后驗證提出的自適應編隊控制策略，證明其可行性.

4.1 算法性能對比仿真結果

為對比IAPF算法與標準的APF算法性能，將標準的L-F無人艇編隊應用于提出的IAPF算法進行避障仿真，仿真對比結果見圖9.APF和IAPF算法采用相同的參數：引力參數2，斥力參數30.由圖9仿真結果可知，改進后的算法IAPF明顯優于標準APF算法.

圖9 APF與IAPF算法對比

4.2 改進的控制策略仿真結果

為驗證本文提出的虛擬跟隨者L-F編隊控制算法的動態調整性能，與標準L-F控制結構進行對比仿真，采用提出的IAPF算法，表3給出了編隊仿真參數，仿真結果見圖10.由圖10b)可知，增加了虛擬跟隨艇后，跟隨艇1與跟隨艇2之間的縱向距離增大，保證了兩艇之間的安全，這種控制結構有利于實現本文提出的自適應編隊控制策略.

圖10 編隊效果對比

L1/mL2/mLV/mφ1φ2φV404040π/6π/60

4.3 自適應編隊控制策略仿真結果

為保證無人艇編隊整體避開靜態障礙物，并且保證跟隨艇之間的安全，對本文提出的自適應編隊控制策略進行仿真驗證，跟隨艇USV1與虛擬跟隨艇USV virtual之間的跟隨角設為15°，結果見圖11～12.

圖12 跟隨角對比結果

由圖11a)可知，跟隨艇1與跟隨艇2均在避障過程中撞到障礙物上，未能安全航行.由圖11b)可知，采用自適應調整跟隨角策略，實現在障礙物附近自動調整角度以避開障礙物，保證跟隨艇安全航行.

圖13為采用自適應調整編隊寬度的策略以通過限制水域的仿真結果，由圖13可知，采用自適應編隊寬度控制策略后，無人艇編隊可以實現自適應調整跟隨角大小，保證安全通過限制水域.跟隨艇的跟隨角變化情況見圖14，在通過限制水域時，跟隨角明顯根據通航水域寬度進行調整.

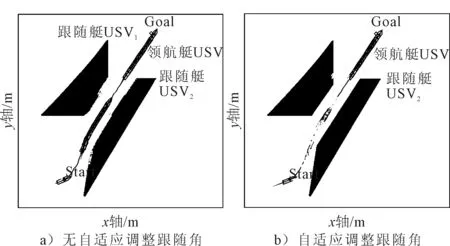
圖13 自適應調整編隊寬度仿真對比結果

圖14 跟隨角對比結果

5 結 束 語

文中采用虛擬跟隨艇建立Leader-Follower無人艇編隊模型，提出自適應編隊控制策略，可根據通航水域寬度和離障礙物的距離進行自適應調整跟隨角，實現不同環境條件下的隊形調整，保證無人艇編隊的整體安全性.針對編隊路徑規劃提出IAPF算法，引入實際船舶在水域中的速度、加速度參量，改進了傳統勢場的勢場力.仿真結果表明，在狹窄水域，無人艇自適應編隊控制策略可以實現動態編隊，實現跟隨艇避開障礙物以及通過狹窄水域，所提出的編隊模型也適用于動態調整編隊結構.