符號(hào)動(dòng)力學(xué)信息熵參數(shù)優(yōu)化方法研究

丁 闖，張兵志,2，馮輔周，吳守軍

（1.陸軍裝甲兵學(xué)院 車輛工程系，北京 100072； 2.北方特種車輛研究所，北京 100072）

符號(hào)動(dòng)力學(xué)信息熵（Symbolic Dynamic Entropy，SDE）能夠有效檢測(cè)振動(dòng)信號(hào)時(shí)間序列的動(dòng)力學(xué)特性[1]，因此，SDE在特征提取及故障診斷中的應(yīng)用越來(lái)越引起人們的重視。SDE具有計(jì)算速度快、對(duì)數(shù)據(jù)量要求小且能捕捉到時(shí)間序列的非平穩(wěn)特性、能夠快速有效提取振動(dòng)信號(hào)的運(yùn)行狀態(tài)等特征。

然而，SDE的計(jì)算結(jié)果受自身參數(shù)的影響比較大，參數(shù)的選擇主要依靠人為經(jīng)驗(yàn)，限制了SDE的應(yīng)用。本文將對(duì)參數(shù)確定的2種觀點(diǎn)進(jìn)行闡述，對(duì)比了2種觀點(diǎn)中參數(shù)確定的典型方法，并通過(guò)對(duì)比優(yōu)化參數(shù)，提高SDE作為特征的算法效率和敏感度。

1 SDE原理

SDE最早由Kurths等提出[2]，計(jì)算方法過(guò)程如下：

設(shè)振動(dòng)信號(hào)序列X={x(i),i=1,2,…N}，即時(shí)域信號(hào)由N個(gè)采樣點(diǎn)元素組成。

（1）振動(dòng)信號(hào)符號(hào)化。將時(shí)間序列X轉(zhuǎn)化到符號(hào)域S={s(i),i=1,2,…,N}，即s(i)代表符號(hào)域S中的第i個(gè)元素。符號(hào)域中符號(hào)使用si表示，其中，si∈{0,1,2,3}，此處si代表符號(hào){0,1,2,3}的具體某個(gè)符號(hào)，具體轉(zhuǎn)化方法為

式中：μ為時(shí)間序列X的平均值，α為權(quán)重，一般取α=0.1[3]。

（2）相空間重構(gòu)。對(duì)符號(hào)域的時(shí)間序列S=進(jìn)行相空間重構(gòu)，得到矩陣S0

其中：m為嵌入維數(shù)，τ為延遲時(shí)間，j=1,2,3,…,K，其中，K=N-(m-1)τ。重構(gòu)矩陣中的每一行S0(j)為一個(gè)重構(gòu)分量，重構(gòu)矩陣中共有K個(gè)重構(gòu)分量。

重構(gòu)矩陣中每個(gè)重構(gòu)分量為一個(gè)獨(dú)立的狀態(tài)模式，由于S0(j)有m個(gè)元素，每個(gè)元素的符號(hào)共有4種可能，因此共有n=4m種狀態(tài)模式。

（3）計(jì)算各狀態(tài)模式出現(xiàn)的概率。統(tǒng)計(jì)各狀態(tài)模式出現(xiàn)的次數(shù)，記為Z(l)(l=1,2,3,…,n)，并計(jì)算其出現(xiàn)的概率，記為

（4）計(jì)算符號(hào)動(dòng)力學(xué)信息熵。

根據(jù)SDE原理，相空間重構(gòu)是算法中的關(guān)鍵一步，其延遲時(shí)間和嵌入維數(shù)的選擇對(duì)SDE的計(jì)算結(jié)果有較大的影響。

2 SDE參數(shù)優(yōu)化

相空間重構(gòu)最早由Takens在1981年提出[4]，關(guān)于延遲時(shí)間τ和嵌入維數(shù)m的選擇，相關(guān)學(xué)者進(jìn)行了大量的研究[5]。

目前對(duì)于參數(shù)選擇有兩種觀點(diǎn)：

(1)延遲時(shí)間和嵌入維數(shù)的選擇互不相關(guān)，即兩者獨(dú)立確定，通常使用互信息法和偽近鄰法相結(jié)合，首先使用互信息法確定延遲時(shí)間，然后在延遲時(shí)間確定后，使用偽近鄰法確定嵌入維數(shù)；

(2)延遲時(shí)間和嵌入維數(shù)的選擇存在聯(lián)系，即兩個(gè)參數(shù)的選擇相互依賴，通常使用關(guān)聯(lián)積分法（即CC算法），通過(guò)構(gòu)造統(tǒng)計(jì)變量和延遲時(shí)間的關(guān)系確定最佳延遲時(shí)間和嵌入窗寬，根據(jù)嵌入窗寬確定嵌入維數(shù)。針對(duì)不同的應(yīng)用需要根據(jù)其具體效果確定參數(shù)選擇的具體方法。

對(duì)于設(shè)備不同運(yùn)行狀態(tài)下的時(shí)域振動(dòng)信號(hào)，采用相同參數(shù)對(duì)其進(jìn)行相空間重構(gòu)，將得到不同的SDE。因此，可使用系統(tǒng)正常狀態(tài)下的振動(dòng)信號(hào)確定的參數(shù)，對(duì)系統(tǒng)不同狀態(tài)下的振動(dòng)信號(hào)進(jìn)行SDE計(jì)算，將熵值作為特征用于判斷系統(tǒng)的運(yùn)行狀態(tài)，從而達(dá)到特征提取的目的。

2.1 延遲時(shí)間和嵌入維數(shù)的獨(dú)立確定方法

（1）基于互信息法確定延遲時(shí)間

對(duì)于振動(dòng)信號(hào)序列X={x(i),i=1,2,…M}，其符號(hào)域的時(shí)間序列S={s(i),1,2,…,N}，為了研究s(i)與s(i+τ)的相關(guān)性，選取延遲序列s(i+τ)構(gòu)成新的序列Q={q(i),i=1,2,…M}，將S與Q的相關(guān)性大小作為確定延遲時(shí)間τ的依據(jù)。根據(jù)信息論理論，兩個(gè)時(shí)間序列的互信息可表示為

式中：Ps(si)和Pq(qi)分別為對(duì)應(yīng)的符號(hào)域時(shí)間序列中事件si和qj的概率，Psq(si,qj)為事件si和qj的聯(lián)合分布概率，此處事件si和qj分別對(duì)應(yīng)相應(yīng)序列的各個(gè)符號(hào)。

對(duì)于某一特定符號(hào)域時(shí)間序列S，其與延遲后的時(shí)間序列Q的互信息值只與延遲時(shí)間有關(guān)，令

式中：I(τ)的大小代表了在已知時(shí)間序列S與時(shí)間延遲后時(shí)間序列Q的相關(guān)性。當(dāng)I(τ)=0時(shí)，表示S和Q完全不相關(guān)；當(dāng)I(τ)取極小值時(shí)，表示S和Q最大可能的不相關(guān)，重構(gòu)過(guò)程中，使用I(τ)的第一個(gè)極小值對(duì)應(yīng)的延遲時(shí)間τ作為最優(yōu)延遲時(shí)間[6]，記為τ0。

（2）基于偽近鄰法確定嵌入維數(shù)

偽近鄰法（False Nearest Neighbor，F(xiàn)NN）是確定最小嵌入維數(shù)的一種有效方法，其計(jì)算過(guò)程為：若嵌入維數(shù)為m時(shí)的重構(gòu)相空間的近鄰點(diǎn)仍然為嵌入維數(shù)為m+1的近鄰點(diǎn)，則此點(diǎn)為真近鄰點(diǎn)，反之若嵌入維數(shù)為m時(shí)的重構(gòu)相空間的近鄰點(diǎn)不是嵌入維數(shù)為m+1的近鄰點(diǎn)，則此點(diǎn)為偽近鄰點(diǎn)。當(dāng)嵌入維數(shù)處于某個(gè)值m時(shí)，偽近鄰點(diǎn)百分比（False Nearest Neighbor Percent，F(xiàn)NNP）將突變下降至0或接近0，且隨著m的增大不再變化，此突變點(diǎn)對(duì)應(yīng)的m值即為所求嵌入維數(shù)，記為m0。

偽近鄰法確定嵌入維數(shù)的具體步驟如下：

當(dāng)嵌入維度為m時(shí)，針對(duì)相空間中的任一重構(gòu)分量S0(j)，在重構(gòu)向量中，與S0(j)歐式距離最近的重構(gòu)向量稱之為S0(j)的最近鄰點(diǎn)，記為SN0N(j)

此時(shí)，有

式中：j≠i，其與重構(gòu)分量S0(j)的距離為

同理，求得嵌入維數(shù)為m+1時(shí)，其重構(gòu)分量S0′(j)與其最近鄰點(diǎn)SN0,Nm+1(j)的距離為Dm+1(j)，此時(shí)可得

引入兩個(gè)偽近鄰點(diǎn)判據(jù)

式中：為符號(hào)域時(shí)間序列Q的均值，Rtol和Atol為選取的閾值。判據(jù)（1）通常用于有限長(zhǎng)無(wú)噪聲的數(shù)據(jù)，判據(jù)（2）通常用于含噪聲的數(shù)據(jù)。

由此可知，重構(gòu)矩陣中的K個(gè)重構(gòu)分量對(duì)應(yīng)K個(gè)最近鄰點(diǎn)，若K個(gè)最近鄰點(diǎn)有l(wèi)個(gè)偽近鄰點(diǎn)，則此時(shí)偽近鄰百分比（即偽近鄰率）為

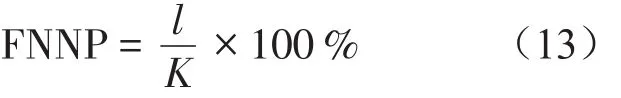
在實(shí)際計(jì)算過(guò)程中，將嵌入維數(shù)m從2開始依次增加，計(jì)算偽近鄰點(diǎn)百分比，直到偽近鄰點(diǎn)百分比小于5%或不再下降時(shí)，此時(shí)的嵌入維數(shù)即為最小嵌入維數(shù)[8]，記為m0。

2.2 延遲時(shí)間和嵌入維數(shù)的聯(lián)合確定方法

延遲時(shí)間和嵌入維數(shù)的聯(lián)合確定通常使用關(guān)聯(lián)積分法（C-C算法），該方法最早由Broomhead和Kim提出，是一種同時(shí)確定最佳延遲時(shí)間和最佳嵌入維數(shù)的算法。其基本思想是通過(guò)嵌入時(shí)間序列的關(guān)聯(lián)積分構(gòu)造能夠代表非線性時(shí)間序列相關(guān)性的統(tǒng)計(jì)量，根據(jù)其和延遲時(shí)間的關(guān)系確定最佳延遲時(shí)間和嵌入窗寬，進(jìn)而確定嵌入維數(shù)。C-C算法是根據(jù)大量的統(tǒng)計(jì)規(guī)律中得到的，具有一定的優(yōu)勢(shì)。

對(duì)于時(shí)間序列X對(duì)應(yīng)的符號(hào)域時(shí)間序列S={s(i),1,2,…,N}，其相空間中的重構(gòu)分量為S0(j)，得出嵌入時(shí)間序列的關(guān)聯(lián)積分方程為

式中：K為相空間矩陣中重構(gòu)向量的數(shù)量，即K=N-(m-1)τ；r為參考半徑，即為閾值；dij為重構(gòu)向量中任一兩個(gè)重構(gòu)分量S0(i)和S0(j)的距離，即dij=‖S0(i)-S0(j)‖ ；H(u)為Heaviside函數(shù)，其取值為

對(duì)于任意的參考半徑r，C(m,τ,N,r)代表任意兩個(gè)重構(gòu)分量的距離小于r的個(gè)數(shù)占總數(shù)的C2K中的比例。對(duì)于符號(hào)域時(shí)間序列S，首先將時(shí)間序列進(jìn)行劃分，分成τ個(gè)長(zhǎng)度相等的時(shí)間序列，τ為延遲時(shí)間。然后構(gòu)造一個(gè)與延遲時(shí)間τ相關(guān)的關(guān)聯(lián)方程：

當(dāng)延遲時(shí)間τ=1時(shí)為單個(gè)時(shí)間序列本身，而此時(shí)，有

當(dāng)延遲時(shí)間τ=2時(shí)，有2個(gè)時(shí)間序列，為和{s(2),s(4),…,s(N)} ，長(zhǎng)度為，而此時(shí)，有

以此類推，可得出當(dāng)延遲時(shí)間τ為任意自然數(shù)時(shí)，其關(guān)聯(lián)方程為F(m,τ,N,r)。

當(dāng)N→∞時(shí)，則

由上式可知，當(dāng)時(shí)間序列中的點(diǎn)為獨(dú)立分布且N→∞時(shí)，所有的F(m,τ,r)均為零。然而實(shí)際序列的長(zhǎng)度為有限值，且時(shí)間序列中的點(diǎn)是相關(guān)的，因此F(m,τ,r)并不是總為零。若參考半徑r為任意值、F(m,τ,r)均為極小值點(diǎn)時(shí)，時(shí)間序列最接近均勻分布。此處，將F(m,τ,r)的最大值和最小值的差定義為

在求解過(guò)程中，Brock等通過(guò)對(duì)各種分布的研究，得出結(jié)論：當(dāng)時(shí)間序列的長(zhǎng)度N≥500時(shí)，對(duì)于嵌入維數(shù)m，一般取2≤m≤5，對(duì)于參考半徑r，一般取為時(shí)間序列的標(biāo)準(zhǔn)差），可得到較好的結(jié)果。而將其應(yīng)用于符號(hào)動(dòng)力學(xué)信息熵特征提取時(shí)，若嵌入維數(shù)取2，得出的信息熵難以區(qū)分故障模式，因此，在計(jì)算時(shí)，可取1,2,3,4。然后構(gòu)造以下3個(gè)統(tǒng)計(jì)量

3 試驗(yàn)驗(yàn)證

為了檢驗(yàn)并對(duì)比參數(shù)優(yōu)化方法的有效性，在SDE取不同參數(shù)條件下對(duì)行星齒輪箱振動(dòng)信號(hào)進(jìn)行特征提取。行星齒輪箱試驗(yàn)臺(tái)如圖1所示。

圖1 行星齒輪箱試驗(yàn)臺(tái)

試驗(yàn)臺(tái)主要由變頻電動(dòng)機(jī)、行星齒輪箱、渦流測(cè)功機(jī)組成，變頻電動(dòng)機(jī)提供動(dòng)力，由渦流測(cè)功機(jī)加載，行星齒輪箱的參數(shù)如表1所示。

表1 行星齒輪箱參數(shù)

分別對(duì)行星齒輪箱齒輪正常、太陽(yáng)輪輪齒局部裂紋故障、行星輪輪齒局部裂紋故障等3種狀態(tài)信號(hào)進(jìn)行分析[7-9]。

此試驗(yàn)中2種狀態(tài)的振動(dòng)信號(hào)均在有負(fù)載情況下完成，其中，變頻電機(jī)輸入轉(zhuǎn)速為2400 r/min，采樣頻率為5120 Hz。正常信號(hào)、太陽(yáng)輪裂紋故障、行星輪裂紋故障時(shí)域波形如圖2所示。

圖23 種狀態(tài)振動(dòng)信號(hào)的時(shí)域波形

（1）SDE信息熵參數(shù)確定

首先利用互信息法計(jì)算正常狀態(tài)下振動(dòng)信號(hào)符號(hào)域時(shí)間序列的延遲時(shí)間τ與互信息之間的關(guān)系，如圖3所示。

圖3 振動(dòng)仿真信號(hào)互信息與延遲時(shí)間的關(guān)系

由圖3可知，互信息第一次取得極小值時(shí)，最佳延遲時(shí)間τ0=8。

當(dāng)輸入延遲時(shí)間τ0=8時(shí)，使用偽近鄰法求解時(shí)間序列的嵌入維數(shù)，使用判據(jù)（2），選擇閾值A(chǔ)tol=2，求出此時(shí)間序列的偽近鄰率與嵌入維數(shù)的關(guān)系如圖4所示，由圖4可知，最佳嵌入維數(shù)m0=3。

使用聯(lián)合積分法即C-C方法確定延遲時(shí)間和嵌入維數(shù)，圖5為由聯(lián)合積分法得出的相關(guān)參數(shù)變化曲線。

由圖5可知，當(dāng)圖中)變化曲線取第1個(gè)零點(diǎn)或接近零點(diǎn)時(shí)，τ0=20，且Fcor(τ)變化曲線取最小值時(shí)，最佳嵌入窗寬τw=25，此時(shí)根據(jù)式（21）可得，m=3；當(dāng)圖中(τ)變化曲線取第一個(gè)極小值時(shí)，τ0=35，同理得m=2。由前文可知，嵌入維數(shù)至少大于2，因此，得出最佳延遲時(shí)間τ0=20，最佳嵌入維數(shù)m0=3。

圖4 振動(dòng)仿真信號(hào)偽近鄰率與嵌入維數(shù)的關(guān)系

圖5 聯(lián)合積分法各參數(shù)的變化曲線

（2）特征提取

取齒輪正常、太陽(yáng)輪裂紋故障、行星輪裂紋故障各20個(gè)樣本，使用SDE計(jì)算3種狀態(tài)下各個(gè)樣本的熵值。使用獨(dú)立方法和聯(lián)合積分法確定參數(shù)的各狀態(tài)下SDE如圖6、圖7所示。

圖6 根據(jù)獨(dú)立確定方法確定參數(shù)的各狀態(tài)SDE

圖7 根據(jù)聯(lián)合積分法確定參數(shù)的各狀態(tài)SDE

為進(jìn)一步突出本文2種方法確定參數(shù)的實(shí)際應(yīng)用效果，在實(shí)際計(jì)算中，增加任意選定的參數(shù)計(jì)算，任意選定延遲時(shí)間τ0=4，嵌入維數(shù)m0=3，此參數(shù)下各狀態(tài)下SDE如圖8所示。

圖8 任意給定參數(shù)的各狀態(tài)SDE

由圖6、圖7、圖8可知，使用獨(dú)立方法確定的參數(shù)計(jì)算得到的3種狀態(tài)下的SDE值相差最大，即分類效果最好，且同種狀態(tài)下的SDE較穩(wěn)定。因此使用互信息法確定延遲時(shí)間，根據(jù)偽近鄰法確定嵌入維數(shù)，具有更好的分類效果。

4 結(jié)語(yǔ)

本文重點(diǎn)研究符號(hào)動(dòng)力學(xué)信息熵參數(shù)優(yōu)化確定方法。根據(jù)其算法原理，使用相空間重構(gòu)的方法確定算法參數(shù)，克服了人為主觀或憑經(jīng)驗(yàn)確定算法參數(shù)的不確定性。根據(jù)當(dāng)前確定相空間參數(shù)的兩種不同觀點(diǎn)，介紹了2種方法中典型參數(shù)確定方法的基本原理，并利用行星齒輪箱實(shí)測(cè)信號(hào)對(duì)所提參數(shù)優(yōu)化方法進(jìn)行了驗(yàn)證。結(jié)果表明，相空間重構(gòu)參數(shù)的獨(dú)立確定方法比聯(lián)合確定方法更優(yōu)，這為符號(hào)動(dòng)力學(xué)信息熵算法中參數(shù)的確定奠定了基礎(chǔ)。