基于EMI技術的小型直流電機振動噪聲研究

張 軍，陸俊峰，袁 翔，丁鵬飛

（安徽理工大學 機械工程學院，安徽 淮南 232000）

電機是一個動力元件，同時也是一個噪聲發生源。電機的振動噪聲在一定程度上直接影響著它的優劣程度和運作的持久性，因此振動和噪聲是決定電機能否充分發揮作用的一個重要因素。不僅僅是工作環境的要求，在日常生活中，安靜、舒適的環境對人的身心健康也極其重要。此外，為了提升本國電機行業在對外貿易上的對抗能力，急需增強對電機振動噪聲的分析以及控制技術的研究[1]。

本文針對某型高檔轎車在調節座椅時會產生頻率在8 kHz左右的高音振動噪聲這個實際問題，先通過對電機定子、轉子進行的聲壓實驗和阻抗模態實驗，確定同頻共振是該振動噪聲產生的原因，在得到有效的峰值頻率后，劃出共振區；通過有限元仿真對定子結構進行優化，得到有效峰值頻率的變化關系，確定了避免定子、轉子產生同頻共振的優化方案，最后結合壓電阻抗技術對實際結構優化后的定子進行阻抗值測量[2]，通過實驗驗證優化方案的可行性，達到了消除電機共振噪聲的目的。

1 EMI壓電阻抗技術

由壓電材料制成的PZT（壓電陶瓷片），當受到外界載荷作用時，引發的微小形變會引起材料的極化現象，符號相異的電荷聚集在PZT的表面，外力越大電荷的聚集程度也就越大，這種表現稱為正壓電效應。反之，當在PZT表面施加電壓，在電場的作用下，PZT內部的正負電荷便向電荷中心產生相對位移，導致PZT的機械變形，稱這種表現形式為逆壓電效應[3-5]。其本質是機械能與電能的相互轉化。

1.1 壓電方程

正壓電效應

標識1、2、3分別對應x、y、z坐標軸方向。dikTk為電位移，為介電矩陣Ej為應力T=0或為固定值時的電位移。

1.2 結構壓電耦合電阻抗原理

通過單自由度SMD系統模型，分析PZT與結構耦合后的動態響應。

機械阻抗Z、激振力F與位移x的關系即

實驗的響應是穩態諧波響應，即

將式(3)簡化為

C為系統阻尼，m為系統質量，ω為激振頻率，ωn為系統諧振頻率，j為虛數單位，KD為系統動態剛度。

1.3 結構壓電耦合電阻抗

實驗所需的PZT與結構進行機電耦合的系統模型如圖1所示。

設所加交變電場為E3=Eˉ3ejωt，可得到PZT的機械阻抗

求解得到PZT的電位移

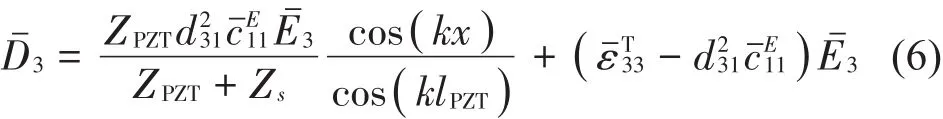
圖1 壓電陶瓷與結構機電耦合模型

則電導納為

在多數實際應用中，tan(klPZT)∕klPZT≈ 1，根據Y=1∕Z，可化簡得到電阻抗為

2 電機的聲壓實驗

先前已通過測量明確電機產生的振動噪聲頻率在8 kHz左右，將進行聲壓實驗確定其產生的原因。

聲壓實驗系統由被測電機、聲級計、高速采集卡以及上位機LABVIEW處理程序組成。分別對定子、轉子進行實驗，通過敲擊的方式進行激振，使電機結構振動從而發出聲音，通過聲級計將聲信號轉換為電信號，并由高速采集卡將聲級計的數據返回上位機，經過快速傅里葉變換將時域信號變為頻域信號，處理之后得到如圖2、圖3所示的定子與轉子聲壓頻域信號圖像。

圖2 定子的聲壓頻域信號圖像

觀察圖2、圖3可知，定子在頻率3487.5 Hz、4437.5 Hz、8312.5 Hz處有明顯的波峰；轉子在頻率3912.5 Hz、8187.5 Hz處有明顯波峰。其中，定子峰值頻率8312.4 Hz與轉子峰值頻率8187.5 Hz十分接近，可初步斷定這是定子轉子的同頻共振產生的噪聲，具體將通過下一節的共振區劃分來進一步明確。

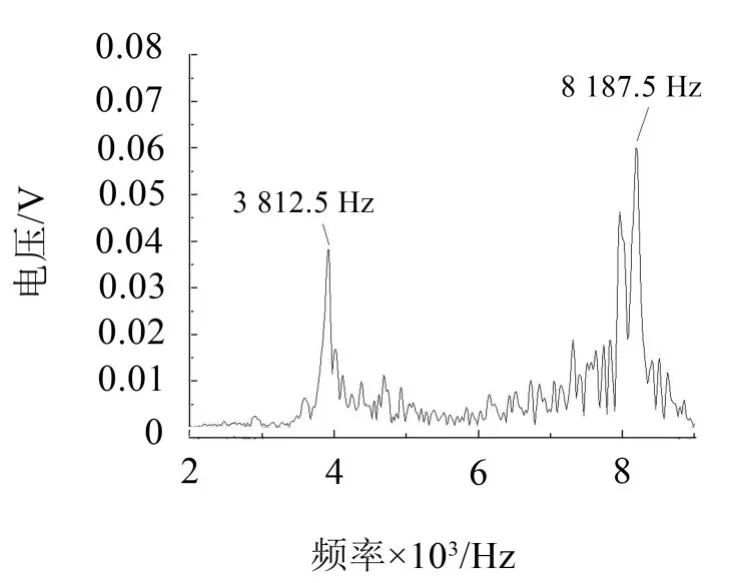
圖3 轉子的聲壓頻域信號圖像

從結果來看，聲壓實驗具有以下特點：

圖像中有較多雜亂的波形，對觀察和提取數據容易造成干擾；對實驗環境要求高，不能有太大的聲音干擾；在激振過程中無法保證每一次的敲擊力度相同，對實驗結果會造成影響。

為排除上述因素帶來的影響，將通過壓電阻抗(EMI)技術對電機進行阻抗模態實驗，進一步明確共振噪聲產生的原因。

3 基于EMI技術的阻抗模態實驗

阻抗模態實驗中將對定子和轉子分別進行阻抗模態頻率分析，如圖4所示實驗系統主要由被測電機、壓電陶瓷片、WK6500B阻抗分析儀組成。

圖4 WK6500B阻抗分析儀以及小型直流電機

阻抗模態測試中將壓電陶瓷與電機進行耦合，依靠阻抗分析儀對壓電陶瓷提供頻率持續改變的1 V正弦電壓，由于正壓電效應，壓電陶瓷會對電機結構施加持續的激振力，并通過阻抗分析儀接收返回信號，得到阻抗圖像。

壓電陶瓷的具體型號可分為PZT-2、PZT-4、PZT-5A、PZT-5 H、PZT-8。其中PZT-4具有優良的信號接收和發射能力[6]，在本實驗中，需要用壓電陶瓷片對電機進行有效激振，因此選擇具有優秀介電和壓電性能的PZT-4作為該實驗壓電材料。

3.1 對定子進行阻抗值測量

對定子進行獨立阻抗值測量，得到如圖5所示的圖像，過小的波峰不是產生同頻共振的原因，為無效峰值頻率，如表1所示為對應掃頻產生的峰值頻率，依據產生的波峰大小將3694.18 Hz和8416.51 Hz定為有效峰值頻率，為方便起見，下文分別稱上述2個頻率為定子的第一有效峰值頻率和定子的第二有效峰值頻率。

圖5 定子阻抗結果

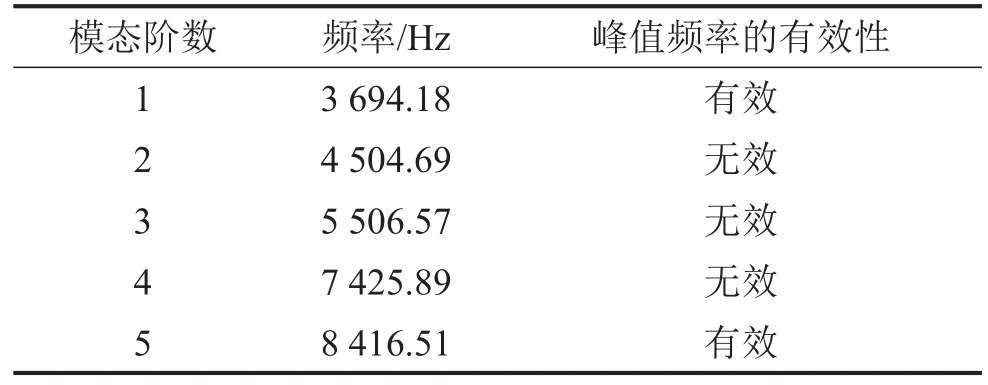
表1 定子固有頻率

3.2 對轉子進行阻抗值測量

圖6是對轉子進行獨立的阻抗值測量得到的圖像，在3945.59 Hz和8200.75 Hz處出現了較為明顯的波峰為有效波峰，提取出轉子的前2階模態，如表2所示。

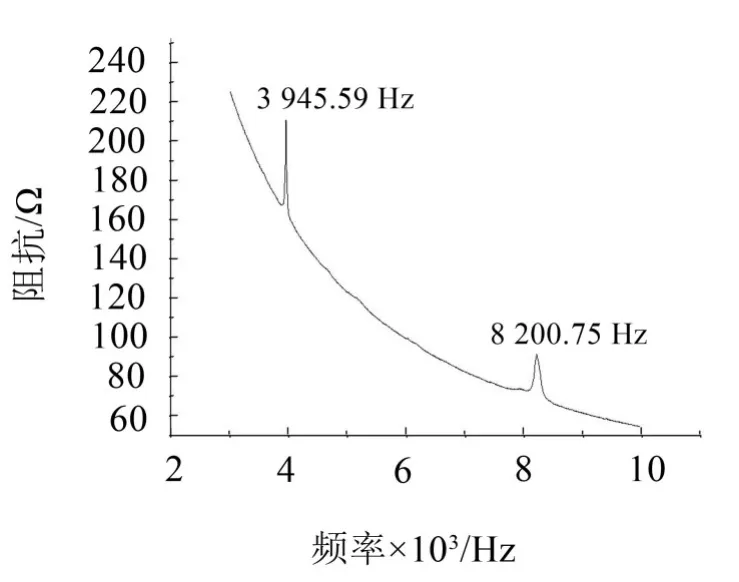
圖6 轉子阻抗結果

表2 轉子固有頻率

為確定有效峰值頻率是否是產生共振的原因，在擁有轉子的2個有效峰值頻率3945.59 Hz、8200.75 Hz之后，根據共振范圍公式將共振區[7]劃分為[0.97f1,1.03f1] ，其中f1為有效峰值頻率，將2個頻率代入可計算得出2個共振區如表3所示。

表3 轉子共振區

上述結果表明定子的第一有效峰值頻率未落入轉子的共振區內，由于頻率值與第一共振區很接近，在接下來的結構優化過程中不排除會進入共振區，因此也將對此重點分析；定子的第二有效峰值頻率落入轉子的第二共振區，這時定子和轉子會擁有相似的振型，從而產生較大的共振噪聲，因此可明確這是產生電機同頻共振的原因。

通過比較可發現阻抗模態實驗與聲壓實驗結果大致相同。同時，基于壓電阻抗技術的阻抗模態實驗得到的圖像目標明顯，曲線平整，無較多雜亂波形；實驗受外界因素影響小，在有較大雜音的環境中，實驗也能順利地進行。由此可以看出壓電阻抗技術在電機振動噪聲研究方面的優越性。

為了使第二有效峰值頻率脫離共振區，同時避免第一有效峰值頻率進入共振區，從而導致新的共振，將通過有限元仿真對電機結構進行優化，以解決共振噪聲的問題。

4 基于有限元仿真的結構優化

有限元法的基本理念是對一個不中斷結構體進行劃分，得到有限個離散的單元，這些單元按照一定形式聯結以模擬被分析對象，每個單元均有特定的節點組合方式，在此基礎上，就可以對其中的單元和材料參數進行定義，對節點進行施加約束函數、載荷函數等操作，再通過求解器求解獲取目標量，從而將一個不中斷區域中不限制自由度的問題變為離散區域中可限制自由度的問題，以解決純理論研究難以攻克的問題。有限元法可求解比較復雜結構，對不規則結構的固有模態計算精度較高[8-10]。

通過上述實驗明確了振動噪聲產生的原因，接下來通過有限元仿真對電機結構進行優化仿真，根據仿真結果中峰值頻率偏移的情況，明確可行的優化方案。

4.1 優化方案

在優化對象的選擇方面，對定子機殼的改動比對轉子構造的改動更為簡易、方便。選取改變電機定子外殼厚度、在定子機殼上增添輻條2種優化方式對定子機殼進行改動。

對定子進行模態仿真分析，將定子劃分為外殼、鐵芯、輻條3個部分，都賦予Solid45單元，各部分之間采用體粘貼(VGLUE)[11-12]，材料參數設置見表4。

4.2 模態仿真

（1）以外殼厚度為變量

對定子網格的劃分如圖5所示。在厚度為影響的模型建立中，忽略了定位臺階及螺孔，對整體模態影響不大，這樣不僅可以減少計算量，還能提高精確度[13]仿真結果如表5所示：

表4 材料參數

表5 模態頻率

觀察表5可以發現，隨著機殼厚度的增加各階模態頻率都有增大的趨勢，且頻率每次升高的變化量也越來越大，可見機殼厚度的增加可升高定子模態頻率。

表6所示為不同機殼厚度工況下模態頻率落入轉子共振區的情況。

表6 模態頻率落入轉子共振區的情況

從機殼厚度與模態頻率變化關系中可以看出，當機殼厚度為7.5 mm時，避開了轉子的各個共振區，因此在改變該小型直流電機機殼厚度避免產生共振噪聲時，7.5 mm可作為參考優化的厚度。對于其他規格的電機，在優化機殼厚度的過程中，應在方案可行的基礎上選取合適的厚度，以避免使電機過于笨重、成本過高。

（2）以輻條數目為變量

圖7所示為定子機殼的網格劃分以及添加輻條后的定子三維模型，將依次對輻條數目從0至8的工況進行模態分析，輻條寬度為10 mm，長度為45 mm，厚度為1 mm，輻條的分布方式均采用均勻分布，表7為模態頻率結果。

圖7 網格劃分和添加輻條后的定子模型

表7 模態頻率

根據表7可知，隨著輻條數增加，第一有效峰值頻率呈現下降趨勢；第二有效峰值頻率呈現上升趨勢。當輻條數為8個的時候，第一和第二有效峰值頻率均沒有出現在轉子共振區，因此當添加8個均勻分布的輻條時，能避免產生共振噪聲，為該方案的最優選擇。

實際實驗中粘連輻條時的第一有效峰值頻率并未落入轉子共振區，且根據仿真結果確定的變化關系來看，隨著輻條數目的增加，第一有效峰值頻率呈下降趨勢，對實際結果不造成影響。

5 基于EMI技術的定子結構優化阻抗模態實驗

實驗中通過添加輻條的方式對上述仿真結果進行驗證，選取2種不同規格的輻條進行實驗，輻條材料均選為矽鋼片，采用錫條焊接的方式將矽鋼片焊于定子機殼處。

2種實驗矽鋼片的規格如下：

規格一：寬度為10 mm，長度為50 mm，厚度為1 mm；

規格二：寬度為10 mm，長度為50 mm，厚度為0.2 mm。

（1）實驗一

采用規格一的輻條依次與機殼黏連，分別獲取的阻抗圖像。圖8所示是定子機殼黏連輻條數依次為0、3、4、7個時的阻抗值，掃頻在3500 Hz～3900Hz和8300 Hz～8650 Hz 2個范圍進行，可以看出隨輻條數的增加第一有效峰值頻率和第二有效峰值頻率均發生較為明顯的偏移。

隨著輻條數的增加，定子的第一有效峰值頻率逐個減小，向左偏移；定子的第二有效峰值頻率逐個增加，向右偏移。依次添加0～8個輻條時的峰值頻率數據以及落入轉子共振區的情況如表8所示。

隨著輻條數的增加，第一有效峰值頻率總體呈下降趨勢，第二有效峰值頻率總體呈上升趨勢，總體變化關系與有限元仿真得到的結果一致。當輻條數為0至8個時，第一有效頻率皆未落在轉子的共振區內，而第二有效峰值頻率僅當輻條數為3個及3個以上時才落在轉子共振區。因此，選擇規格一的矽鋼片作為輻條的情況下，輻條數目添加到3個及3個以上時，第一有效峰值頻率和第二有效峰值頻率都脫離了轉子共振區，避免了共振噪聲的產生。

圖8 阻抗值對比

表8 兩部分頻率值數據(用規格一的輻條)

（2）實驗二

用規格二的輻條進行實驗獲取阻抗圖像。

圖9所示是定子機殼黏連輻條數依次為0、4、6、8個時的阻抗值，掃頻在3300 Hz～4100 Hz和8350 Hz～8550 Hz兩個范圍進行。

與實驗一有相同偏移趨勢，定子的第一有效峰值頻率隨輻條數的增加而減小；第二有效峰值頻率隨輻條數增加而增大。依次添加0～8個規格二的輻條所得的具體數據以及與落入轉子共振區的情況如表9所示。

隨著輻條數的增加，第一有效峰值頻率總體呈下降趨勢，第二有效峰值頻率總體呈上升趨勢，與有限元仿真結果一致。當輻條數為0～8個時的第一有效頻率皆未落在轉子的共振區內，而第二有效峰值頻率僅當輻條數為7個及7個以上時才落在轉子共振區。因此對于規格二的矽鋼片作為輻條的情況，添加的輻條數目為7個及7個以上時，第一有效峰值頻率和第二有效峰值頻率皆脫離了轉子共振區，避免了共振噪聲的產生。

對比兩組厚度不同輻條的實驗結果，可知當輻條其他屬性不變時，厚度越大，對有效峰值頻率的影響越大，其偏移的程度也就越大，在具體添加輻條的時候可以通過增加輻條的厚度來減少所用的輻條數量，以達到相同的目的。

表9 兩部分頻率值數據(用規格二的輻條)

6 結語

(1)通過對問題電機進行聲壓實驗和壓電阻抗模態實驗，確定了8 kHz處的同頻共振是噪聲產生的原因。壓電阻抗技術相對于傳統聲學采集方法，具有成像清晰、平整、激振穩定、對實驗環境的安靜程度要求不高等優點。

(2)阻抗頻率的變化反映的是機械構造上的變化，通過測得的有效峰值頻率劃分了共振區，確定了改變機殼厚度和增添輻條的2種優化方案。

(3)通過理論、仿真與實驗相結合的方法，依照出現問題、找出原因、確定方案、付諸實踐的研究路線，制定增添輻條方案并進行了實驗，結果可知：通過增加輻條數能夠使有效峰值頻率脫離共振區以達到避免產生共振噪聲的目的。實驗與仿真所表現出的頻率變化關系基本一致，驗證了有限元仿真的準確性，并說明壓電阻抗技術對電機振動噪聲的研究具有一定的實際意義。

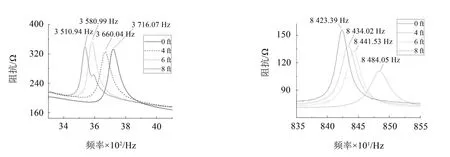
圖9 阻抗值對比