基于Berg模型橡膠襯套的汽車平順性分析

張艷龍，李 彪，王 麗，孫紹軒

(1.蘭州交通大學(xué) 機(jī)電工程學(xué)院，蘭州 730070；2.中國鐵路蘭州局集團(tuán)有限公司 蘭西車輛段，蘭州 730070；3.蘭州城市學(xué)院 數(shù)學(xué)學(xué)院，蘭州 730070)

隨著汽車行駛平順性的研究日益受到重視，需要分析出影響汽車行駛平順性振動(dòng)響應(yīng)量的主要因素，進(jìn)而提出改進(jìn)的方法措施。而現(xiàn)代汽車懸架系統(tǒng)中大量應(yīng)用橡膠襯套等彈性元件，其對(duì)于改善懸架彈性運(yùn)動(dòng)學(xué)性能、有效減弱路面不平度激勵(lì)引起的振動(dòng)發(fā)揮重要作用。陶向華等基于人-車-路相互作用建立簡(jiǎn)化的3質(zhì)量車輛模型，利用所建的簡(jiǎn)化車輛模型對(duì)車輛的振動(dòng)特性進(jìn)行了評(píng)價(jià)[1]。李杰等基于虛擬激勵(lì)法，推導(dǎo)1/2汽車4自由度系統(tǒng)振動(dòng)的頻率響應(yīng)特性，建立求取汽車系統(tǒng)振動(dòng)響應(yīng)量及其功率譜密度的公式，給出了求解汽車振動(dòng)響應(yīng)量功率譜密度的算例[2]。徐中明等依據(jù)國際標(biāo)準(zhǔn)ISO2631，對(duì)某客車進(jìn)行行駛平順性試驗(yàn)，研究了時(shí)、頻兩種算法在平順性分析中的差別[3]。于增亮等針對(duì)目前應(yīng)用的Kelvin-Voigt模型、3參數(shù)Maxwell模型、Berg模型和DZIERZEK模型進(jìn)行模型結(jié)構(gòu)特征、參數(shù)識(shí)別方法與特性預(yù)測(cè)精度的對(duì)比分析[4]。左曙光等建立一種能準(zhǔn)確描述其動(dòng)態(tài)特性的理論模型，通過試驗(yàn)得到了橡膠襯套軸向的靜、動(dòng)態(tài)特性，對(duì)其頻率相關(guān)性和振幅相關(guān)性進(jìn)行了分析[5]。目前單獨(dú)研究橡膠襯套的材料性能較多，將非線性襯套與車輛振動(dòng)相結(jié)合的研究相對(duì)較少[6-14]。

為了更好體現(xiàn)出橡膠襯套動(dòng)態(tài)特性的振幅依賴性，本文應(yīng)用Berg模型描述橡膠襯套的摩擦效應(yīng)，建立含有摩擦特性的3自由度車輛垂向模型，分析Berg模型摩擦特性對(duì)車輛振動(dòng)響應(yīng)量和人體加權(quán)加速度均方根值的影響，進(jìn)而分析橡膠襯套對(duì)汽車平順性的影響。

1 含有摩擦特性的車輛振動(dòng)模型

為了分析基于Berg模型的橡膠襯套對(duì)汽車平順性的影響，建立如圖1所示的含摩擦特性的3自由度車輛垂向振動(dòng)模型。

圖1 車輛振動(dòng)模型

圖中mp為人體質(zhì)量之半，ms為車身部分質(zhì)量，mt為輪胎質(zhì)量，其值分別為30 kg、230 kg、30 kg；kp為座椅剛度之半，ks為車身懸架剛度，kt為輪胎剛度，其值分別為9950 N/m、20200 N/m、128000 N/m；cp為座椅阻尼之半，cs為懸架阻尼，其值分別為264 N·s/m、1137 N·s/m(考慮到車輛左右對(duì)稱，在車輛模型參數(shù)選取時(shí)，mp、kp和cp分別為人體質(zhì)量、座椅剛度和阻尼之半[1])；zp、zs、zt、z1分別為人體垂直位移、車身垂直位移、車輪垂直位移及摩擦單元垂直位移，z2為串聯(lián)彈簧k1與串聯(lián)阻尼c之間的垂直位移，單位為m；q表示為路面不平度，單位為m；圖1虛線框內(nèi)所示為Berg模型，F(xiàn)f為Berg模型中的摩擦力，單位為N；k1、k2、c1、x2的取值見表1。

表1 Berg模型參數(shù)

由拉格朗日方程可得到3自由度車輛模型的微分方程組為

Berg模型的摩擦力Ff取決于摩擦單元兩端的相對(duì)位移，同時(shí)也與摩擦力位移曲線上的參考點(diǎn)(xs,Ffs)有關(guān)，其具體表達(dá)形式為

當(dāng)x=xs時(shí)，

當(dāng)x＞xs或x增加時(shí)

當(dāng)x＜xs或x減小時(shí)

其中：Ffmax為最大摩擦力；x2為摩擦力Ff從0開始逐漸增加至Ff=F∕2時(shí)的位移值

fmax取值為-1～1。

國際標(biāo)準(zhǔn)化組織建議路面功率譜密度Gq(n)用下式作為擬合表達(dá)式

式中：n為空間頻率，單位m-1，它是波長(zhǎng)的倒數(shù)，表示每米長(zhǎng)度中包含幾個(gè)波長(zhǎng)；n0為參考空間頻率，n0=0.1m-1；Gq(n0)為參考空間頻率n0下的路面功率譜密度值，稱為路面不平度系數(shù)，單位為m2∕m-1=m3；w為頻率指數(shù)，w=2，為雙對(duì)數(shù)坐標(biāo)上斜線的斜率，它決定路面功率譜密度的頻率結(jié)構(gòu)。

用三角級(jí)數(shù)法對(duì)路面進(jìn)行模擬作為車輛振動(dòng)輸入。以B級(jí)路面為例，車速v為20 m/s，仿真結(jié)果如圖2所示。

圖2 B級(jí)路面隨機(jī)激勵(lì)

2 車輛振動(dòng)仿真分析

將車輛振動(dòng)方程組轉(zhuǎn)換成狀態(tài)方程，并結(jié)合路面隨機(jī)激勵(lì)，采用4階龍格庫塔法進(jìn)行數(shù)值積分可得到響應(yīng)的時(shí)間歷程曲線，并通過FFT變換得到相應(yīng)量的功率譜密度曲線。

2.1 汽車振動(dòng)響應(yīng)量的仿真分析

圖3(a)和圖3(b)分別為系統(tǒng)在時(shí)域中的人體加速度和懸架動(dòng)撓度的仿真曲線。從圖中可以看出：相較于未考慮橡膠襯套，考慮橡膠襯套時(shí)曲線值在不同程度上都有所減小。在圖3(a)中，當(dāng)t在1.1 s和6.7 s時(shí)，2個(gè)振動(dòng)加速度的峰值都明顯減小，并且當(dāng)考慮橡膠襯套時(shí)，人體振動(dòng)加速度基本都在-1 m/s2～1 m/s2之間。在圖3(b)中，當(dāng)t在0～2 s區(qū)間內(nèi)，可以明顯發(fā)現(xiàn)在考慮橡膠襯套時(shí)懸架動(dòng)撓度都大幅度減弱，在考慮橡膠襯套時(shí)懸架動(dòng)撓度也基本在-0.008 m～0.008 m之間。可以得出，在考慮Berg橡膠襯套的摩擦特性后，汽車在時(shí)域上的振動(dòng)響應(yīng)量都有不同程度減小，說明其有效地減弱了振動(dòng)。

對(duì)時(shí)域響應(yīng)量進(jìn)行FFT變換可以得到其對(duì)應(yīng)的功率譜密度曲線，如圖4(a)和圖4(b)所示。

圖3 時(shí)間歷程曲線對(duì)比圖

圖4 功率譜密度曲線對(duì)比圖

在圖4(a)中，由人體加速度功率譜密度圖可知：未考慮橡膠襯套時(shí)和考慮橡膠襯套時(shí)的共振頻率分別為1.22 Hz和1.17 Hz，可見橡膠襯套的摩擦特性使人體的共振頻率減小了4.1%。同時(shí)也可以看到，在考慮橡膠襯套后人體加速度功率譜幅值降低33%。圖4(b)為懸架動(dòng)撓度功率譜密度圖，可以得出在未考慮橡膠襯套和考慮橡膠襯套后的共振頻率分別為1.21 Hz和1.03 Hz，此外在考慮橡膠襯套后懸架動(dòng)撓度功率譜幅值降低16%。可以得出，在考慮Berg橡膠襯套的摩擦特性后，汽車在頻域上振動(dòng)響應(yīng)量的功率譜密度值也都在不同程度減小，尤其是在幅值處減小更顯著，說明其消耗了振動(dòng)能量。

2.2 Berg模型參數(shù)對(duì)人體加速度的影響

圖5是Berg模型中k1、k2和c3個(gè)參數(shù)在原值及原值的1.5倍、0.5倍時(shí)人體加速度時(shí)間歷程曲線。從圖5(a)中可以看到，當(dāng)k1值較小時(shí)在時(shí)間歷程曲線中的對(duì)應(yīng)峰值反而越大。從圖5(b)可以得到，當(dāng)k2取值為原值時(shí)人體加速度最大，當(dāng)k2的值大于或小于該值時(shí)人體加速度都會(huì)減小。從圖5(c)中可以看到，c的取值對(duì)人體加速度幾乎沒有影響。

對(duì)以上時(shí)域響應(yīng)量進(jìn)行FFT變換可以得到Berg模型中k1、k2和c3個(gè)參數(shù)變化時(shí)對(duì)應(yīng)的人體加速度功率譜密度曲線，如圖6圖所示。在圖6(a)中，當(dāng)k1取原值時(shí)人體的共振頻率為1.12 Hz，加速度功率譜密度為0.37 m2/s3。當(dāng)k1取1.5倍原值時(shí)，其共振頻率減小為1.06 Hz，功率譜密度幅值較原值減小了29.3%。當(dāng)k1取0.5倍原值時(shí)，其共振頻率增大為1.19 Hz，功率譜密度幅值較原值增大了21.1%。可見k1的取值與人體加速度功率譜呈負(fù)相關(guān)。在圖6(b)中，可以看到當(dāng)k2的值大于或小于其原值時(shí)所對(duì)應(yīng)的功率譜密度值都會(huì)減小，且在幅值處更為顯著。在圖6(c)中，3條曲線基本重合在一起，可見c的取值對(duì)于人體加速度功率譜密度的影響相對(duì)較小。

2.3 人體加權(quán)加速度均方根值的仿真分析

根據(jù)ISO2631標(biāo)準(zhǔn)規(guī)定[9]，對(duì)人體加速度時(shí)間歷程a(t)進(jìn)行頻譜分析，得到功率譜密度函數(shù)Ga(f)；再根據(jù)式(6)即可計(jì)算出頻率加權(quán)后的垂向加速度均方根awk

其中垂向頻率加權(quán)函數(shù)

圖5 不同Berg參數(shù)下的人體加速度

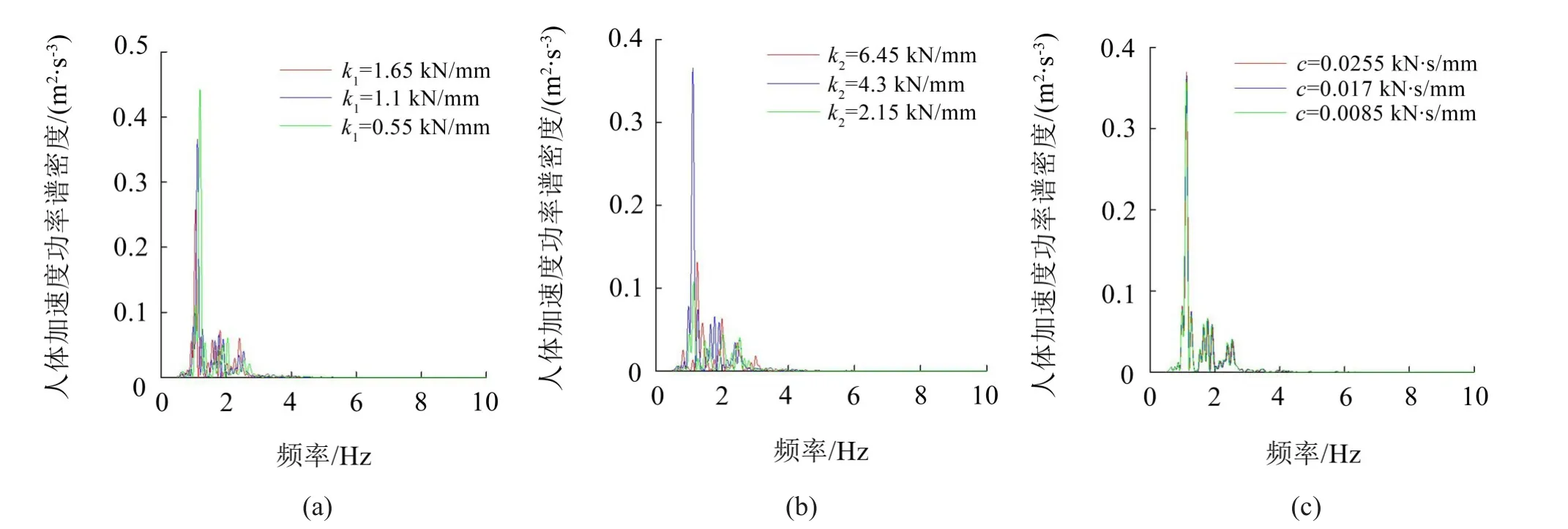
圖6 不同Berg參數(shù)下的人體加速度功率譜密度

將所求得的值和加權(quán)加速度均方根值與人的主觀感覺進(jìn)行對(duì)比，即可分析出舒適程度。從圖7(a)和圖7(b)可以看出，隨著座椅剛度和懸架剛度增大，其加權(quán)加速度均方根值也增大。相比未考慮橡膠襯套，在同一剛度下的加權(quán)加速度均方根值較前者減小0.018左右，并且兩者的差值呈增大的趨勢(shì)。從圖7(c)和圖7(d)可以看出，隨著輪胎剛度和座椅阻尼值增大，其加權(quán)加速度均方根值不同程度減小，從圖7(d)中可以看到座椅阻尼值對(duì)加權(quán)加速度均方根值的影響曲線比較平滑。同一座椅阻尼值下考慮橡膠襯套時(shí)的值比未考慮橡膠襯套時(shí)減小0.02左右，而隨著輪胎剛度增大，考慮橡膠襯套時(shí)的加權(quán)加速度均方根值與未考慮橡膠襯套時(shí)的差值越來越大。從圖7(e)可以得到，隨著懸架阻尼增大，考慮橡膠襯套時(shí)和未考慮橡膠襯套時(shí)的變化趨勢(shì)是不同的。未考慮橡膠襯套時(shí)，懸架阻尼和座椅阻尼的增大都使得加權(quán)加速度均方根值減小，而考慮橡膠襯套之后，隨著懸架阻尼增大，加權(quán)加速度均方根值增大，并且增大的趨勢(shì)很明顯。從圖7(e)可以明顯看到由于考慮Berg摩擦特性致使加權(quán)加速度均方根值的變化曲線較為曲折。考慮橡膠襯套和未考慮橡膠襯套時(shí)，不同的汽車懸掛參數(shù)對(duì)人體加權(quán)加速度均方根值的影響趨勢(shì)不完全相同，考慮橡膠襯套時(shí)也應(yīng)注意不同懸掛參數(shù)給舒適性帶來的影響，應(yīng)該綜合考慮以選擇恰當(dāng)?shù)膮?shù)值。

2.4 Berg模型參數(shù)對(duì)awk的影響

圖8是Berg模型中k1、k2和c從其原值0.5倍左右一直增大到其原值的1.5倍左右時(shí)人體加權(quán)加速度均方根值的變化曲線。在圖8(a)中，隨著k1增大，其對(duì)應(yīng)的加權(quán)加速度均方根值逐漸減小。由圖8(b)可以得到，隨著k2增大，其加權(quán)加速度均方根值先基本不變，后增大，再減小。從圖8(c)中可以看到，隨著c值增大，其所對(duì)應(yīng)的加權(quán)加速度均方根值也逐漸增大。

3 結(jié)語

通過將Berg模型橡膠襯套加入車輛懸掛系統(tǒng)，建立含有Berg摩擦特性的車輛振動(dòng)模型。根據(jù)拉格朗日方程得到系統(tǒng)的運(yùn)動(dòng)微分方程，以隨機(jī)路面作為激勵(lì)，得出一些系統(tǒng)振動(dòng)響應(yīng)量。從分析結(jié)果可知：

(1)在時(shí)域上，由于考慮了碳黑增強(qiáng)劑的摩擦效應(yīng)，Berg模型對(duì)人體加速度和懸架動(dòng)撓度起到了減小作用，尤其在峰值處產(chǎn)生的效果更加明顯；

(2)在頻域上，在考慮橡膠襯套后其響應(yīng)量的功率譜密度曲線都有所降低，尤其在幅值處比較顯著，表明其有效地減弱了振動(dòng)；

(3)Berg模型中k1與人體加速度功率譜呈負(fù)相關(guān)關(guān)系，k2為原參數(shù)值時(shí)功率譜密度最大，c對(duì)功率譜密度的影響很小；

(4)依據(jù)ISO2631-1:1997(E)，選取豎直方向加速度的加權(quán)值作為評(píng)價(jià)標(biāo)準(zhǔn)評(píng)價(jià)乘客的主觀感受，結(jié)論為沒有不舒適。考慮橡膠襯套后加權(quán)加速度均方根值較之前未考慮時(shí)的值在不同程度上都有所減小，并且隨著座椅剛度和懸架剛度值增大，其加權(quán)加速度均方根值呈增大趨勢(shì)。隨著輪胎剛度和座椅阻尼值增大，其加權(quán)加速度均方根值呈減小趨勢(shì)。對(duì)于懸架阻尼而言隨著其值增大，未考慮橡膠襯套時(shí)呈負(fù)相關(guān)，而考慮橡膠襯套時(shí)呈正相關(guān)。

圖7 懸掛參數(shù)對(duì)人體加權(quán)加速度均方根值的影響對(duì)比圖

圖8 Berg模型參數(shù)對(duì)人體加權(quán)加速度均方根值的影響圖

（5）對(duì)于Berg模型參數(shù)而言，隨著k1增大，加權(quán)加速度均方根值呈減小趨勢(shì)，隨著k2增大，加權(quán)加速度均方根值呈先基本不變，后增大，再減小趨勢(shì)。隨著c增大，加權(quán)加速度均方根值呈增大趨勢(shì)。

綜上可以得到，Berg模型的摩擦特性能夠有效減弱車輛振動(dòng)，提高汽車平順性。分析時(shí)應(yīng)綜合考慮橡膠襯套和車輛懸掛系統(tǒng)參數(shù)對(duì)系統(tǒng)振動(dòng)的影響，這可為提高汽車平順性提供部分理論參考。