金屬O形環力學性能仿真分析與試驗驗證

張文昌 勵行根2 魏世軍2 賈曉紅 郭 飛

(1.清華大學摩擦學國家重點實驗室 北京 100084；2.寧波天生密封件有限公司 浙江寧波 315302)

金屬O形環(以下簡稱O形環)是核反應堆壓力容器中常用的密封，具有大接觸應力、耐高溫、耐腐蝕等優點。O形環密封系統主要由封頭或上法蘭、筒體端部或下法蘭、O形環及其他必要的緊固件組成。O形環一般采用金屬圓管彎制焊成，常在外表面涂或鍍銀等塑性較好的材料以提高密封性能。

O形環自身的力學性能對其密封性能影響顯著。密封環通過形變，增加工質在密封界面的流動阻力從而形成密封。受到軸向載荷時O形環的壓縮特性反映了密封環表面與法蘭表面形成初始密封的能力。而當密封系統在實際工況下，由于螺栓及法蘭的形變，使得法蘭接觸面與O形環接觸面產生了相對分離的趨勢。此時O形環的回彈能力對于該密封系統連接的緊固程度有較大的影響[1]。

通過研究O形環的力學性能可以為其產品設計和改進、質量監督、密封性能監控等工作提供依據。自1960年美國首次將空心金屬O形環應用于反應堆始，各國研究者陸續針對O形環密封特性[2]、形變特性[3]、截面結構[4]以及材料的超塑性[5]、低溫高周疲勞性能[6]、長時間組織穩定性[7]等開展了大量研究，同時總結了大量經驗設計方法并開展了相關仿真分析方法研究[8-11]。但主要研究成果集中于O形環的壓縮回彈特性的試驗和經驗模型。

本文作者旨在以核反應堆壓力容器用金屬O形環為研究對象，考慮密封環的復合結構、材料彈塑性特征和工況條件，采用有限元方法建立O形環力學性能仿真模型，分析密封環的壓縮回彈特性、應力應變特征、接觸特性以及銀層的作用，并進行相關試驗驗證。

1 有限元模型和試驗方法

壓力容器中采用了雙道O形環，由于內側與外側O形環力學特性相同，在此只選取內側O形環進行建模。O形環主體部分是φ12.7 mm×1.27 mm的空心環，由Inconel 718合金管材無縫焊接而成，表面鍍有厚度為0.15～0.22 mm的銀層。

O形環的力學仿真涉及材料彈塑性、密封圈結構大變形以及接觸非線性，根據O形環結構和受力特點，建立如圖1所示的平面二維軸對稱模型以提高計算效率。

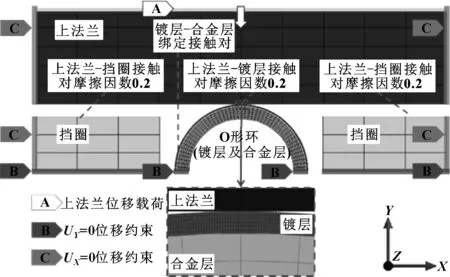
圖1 金屬O形環密封系統的有限元模型

上下法蘭為線彈性不銹鋼材料，O形環Inconel718合金及銀層采用多線性等向強化(MISO)材料模型。幾何模型繞軸線(Y軸)為對稱軸，施加對稱約束條件，上法蘭與擋圈施加UX=0位移，在上法蘭施加Y向位移載荷。取最大壓縮量為2.4 mm，由于上下法蘭對稱性，上法蘭壓縮量為1.2 mm；卸載時，將原施加UY=-1.2 mm載荷逐漸減小，直至O形環與法蘭脫離，模擬密封系統使用過程容器內充氣、 容器內壓的變化等因素引起的法蘭分離。加卸載過程為準靜態。

壓縮回彈特性測量試驗在圖2所示的墊片綜合性能試驗機上進行，包括液壓機(YJN-100)、位移傳感器NS-WY02-20-5(精度：0.05%)、力傳感器BLR-1(靈敏度：1 mV/V)。參照GB/T 12622中墊片壓縮回彈特性的測量方法，在室溫20 ℃環境下以0.5 MPa/s的速率加載卸載，測量墊片的應力與變形關系。由于仿真環和實驗環直徑不同，采用線比壓進行比較，如圖3(a)所示。

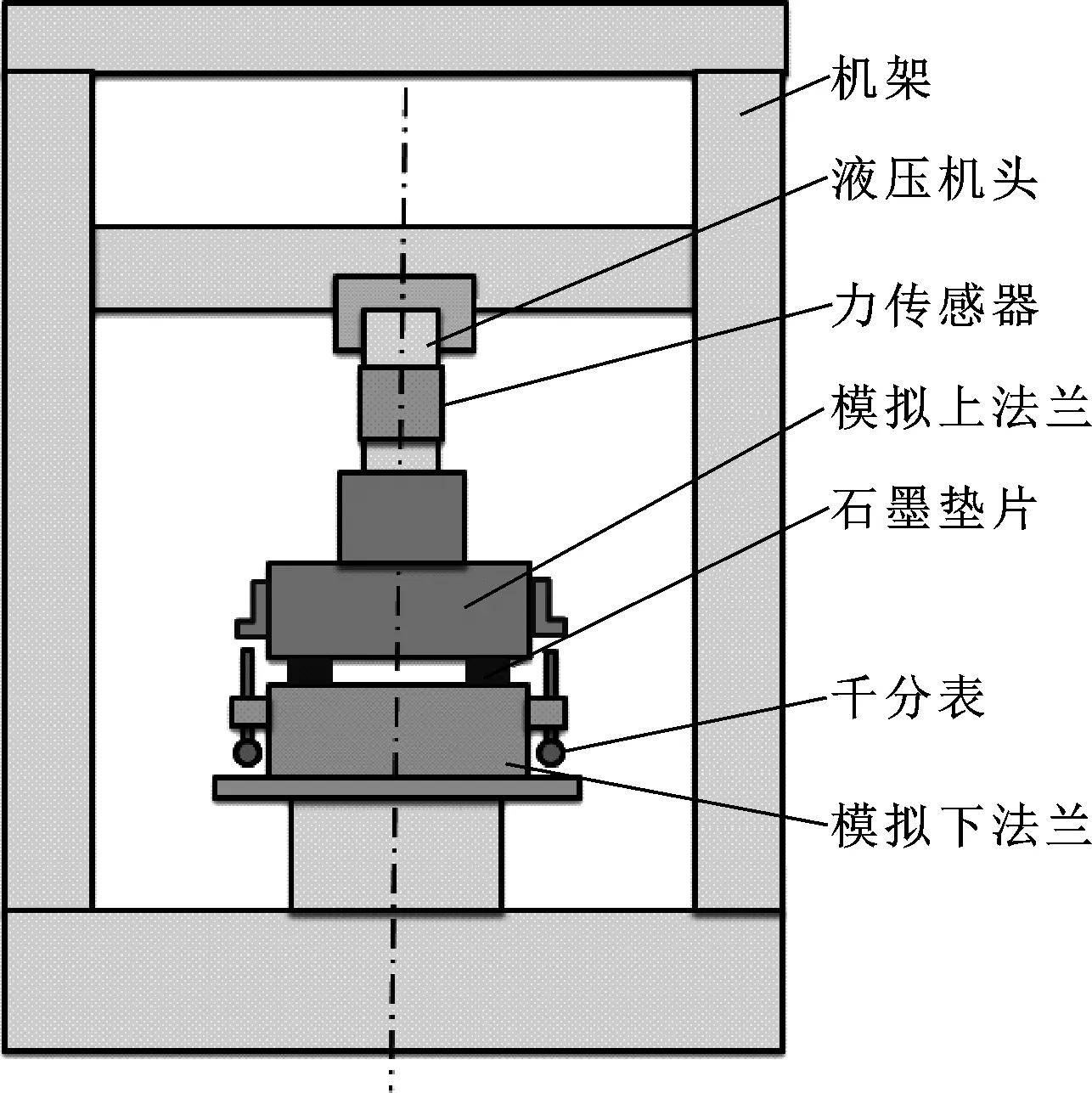
圖2 墊片綜合性能試驗機示意圖

2 力學特性結果分析

2.1 壓縮回彈特性

O形環的壓縮回彈特性反映了預緊狀態下初始密封的形成能力和操作工況下密封的保持能力和裕量，是衡量O形環力學性能的主要指標。O形環的軸向載荷F-壓縮率η曲線反映了O形環的壓縮回彈特性，圖3(b)給出了F-η壓縮回彈曲線。

圖3(b)所示曲線包括了彈性變形區、塑性變形區和法蘭接觸區，仿真計算和試驗測量的各段區域分界點和變化趨勢具有很好的一致性。以最大壓縮率

為18.5%時的O形環壓縮回彈特性曲線為例。加載過程可以分為3個區域：(1)加載初期，載荷隨壓縮率呈線性增長趨勢，此時為彈性變形區；(2)加載中期，當壓縮率達到2%附近時，開始進入塑性變形區，O形環鍍層與合金層作為整體，其整體剛度降低；(3)加載后期，上下法蘭發生接觸后繼續加載，進入法蘭接觸區，由于法蘭剛度較大，軸向載荷突然增大，且與壓縮率呈線性關系陡增，當達到最大壓縮率18.5%時軸向載荷已經達到105kN量級。

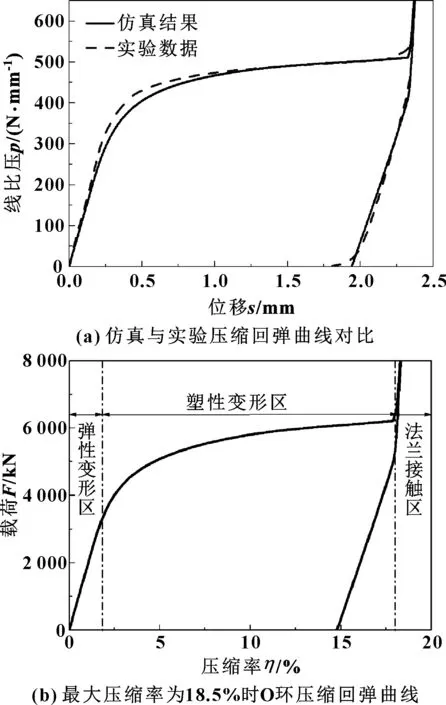
圖3 仿真與試驗結果對比及O形環壓縮回彈曲線

卸載過程，由于法蘭處于彈性變形范圍，因此加載卸載曲線均與壓縮率呈近似線性關系；持續卸載O形環進入塑性變形區后，O形環的塑性形變保留，彈性形變開始恢復，O形環產生回彈，最終完全卸載后仍然有部分殘余形變。不同曲線在加載段幾乎重合，卸載段卸載起點不同，但卸載段除進入法蘭接觸區的部分受到剛性較大的法蘭的影響，其余卸載段曲線基本互相平行。

2.2 接觸特性

圖4給出了加載過程中O形環和上法蘭接觸壓力的變化規律，取壓縮率分別為0、1%、3%、7%、10%，以及完全加載即壓縮率為18.5%，作出接觸壓力曲線。橫軸為有限元模型中的X坐標，零點表示O形環原始外徑最高點，即與法蘭的切點。

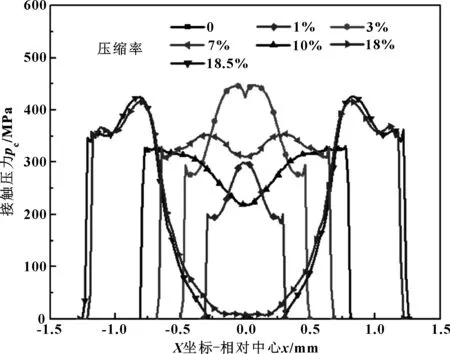
圖4 加載過程接觸壓力變化

O形環經過有限元離散化處理并非嚴格的圓形，法蘭和O形環初始相切的位置，也有很小的接觸壓力，這屬于離散化帶來的誤差。因為數值很小，所以可以忽略不計。當壓縮率較小(載荷較小)時，O形環徑向最高點與法蘭接觸，接觸壓力分布近似為倒U形；隨著載荷增大，接觸寬度和接觸壓力都隨之增大。當壓縮率達到約3%時，接觸寬度進一步增大，但是接觸壓力則有所減小，尤其接觸區中間壓力更小，出現內凹。隨著壓縮率進一步增加，接觸區寬度增大，最大接觸壓力減小，接觸壓力內凹程度也繼續增大。當壓縮率達到17.8%時，法蘭和擋環開始接觸。可以看出，當法蘭和擋環開始接觸后，O形環與法蘭的接觸區中間部分近似脫離接觸，接觸區中間開始凹陷，在凹陷區兩側出現對稱的2個接觸區；隨著壓縮率的增大，O形環與法蘭之間的接觸壓力基本不變，增大的載荷由擋環承擔，所以擋環與法蘭之間的壓力隨載荷增大而增大。

接觸寬度在加載和卸載過程中也因塑性變形而變化。分析接觸寬度的變化會發現其與圖3所示的壓縮回彈特性曲線具有相同的特征。

2.3 應力應變特征

圖5所示為等效彈性應變最大值、等效塑性應變最大值及等效應變最大值隨壓縮率變化的曲線。

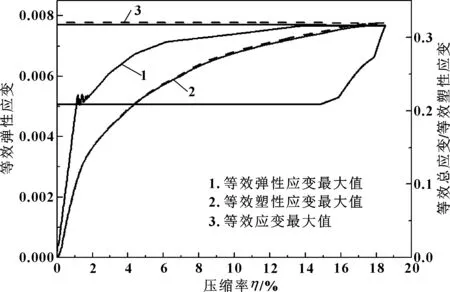
圖5 O形環等效應變最大值變化

可以看出彈性應變在加載初期較快地接近其最大值，在壓縮率為0～1%之間，彈性應變最大值呈線性增長，壓縮率達到1%附近后其最大彈性應變達到0.005即其屈服極限，應變值上下抖動，材料開始發生塑性變形，進入流動階段；繼續增加壓縮率，O形環進入強化階段，材料恢復了對變形的抵抗能力。卸載時由于O形環發生了塑性形變，因此塑性應變最大值保持不減，卸載階段彈性應變最大值隨卸載而減小，但并未完全消失，而是由于各部分變形量不同，回彈過程中各部分要恢復的彈性變形不同，各部分之間為了變形協調就會產生一定的相互約束，導致了在完全卸載后仍然留下一定的殘余應變。

圖6給出了O形環完全加載時各節點的位移矢量。可以看出：O形環中心部分節點以Y軸位移為主，左側部分節點以X軸位移為主，且徑向位移小于軸向位移。位移矢量長度最小節點約處在截面40°處，其位移矢量方向基本與初始輪廓相切。

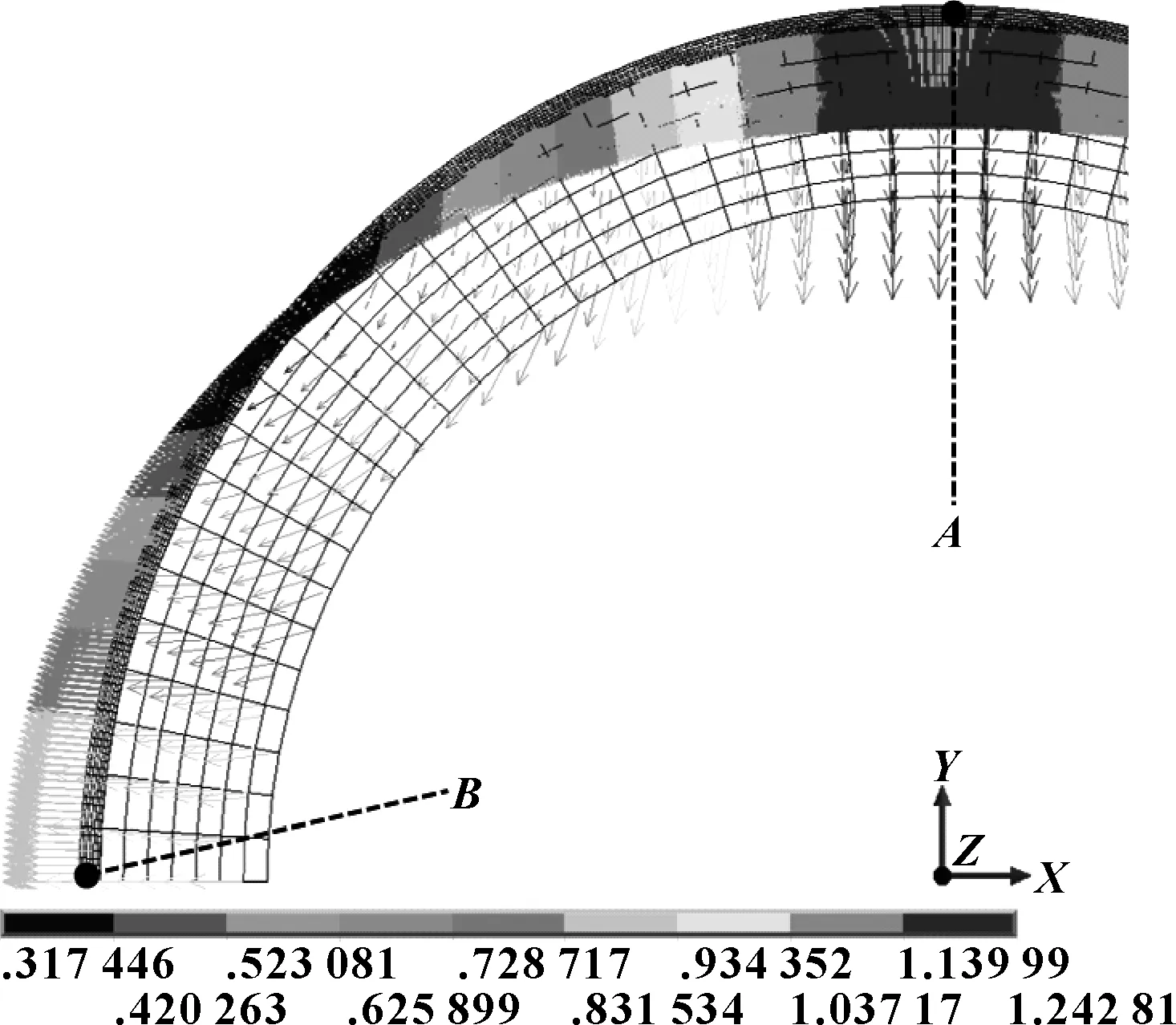
圖6 完全加載各節點位移矢量

3 鍍銀層影響分析

鍍層的存在及其厚度是影響O形環力學特征的一個因素，圖7給出了3種鍍層狀態及不同鍍層厚度下O形環的壓縮回彈曲線。3種狀態分別為：(1)公稱尺寸狀態，即存在鍍層，外徑d=13 mm，鍍層厚度γ=0.15 mm；(2)無鍍層狀態，即僅存在合金層，O形環外徑d=12.7 mm；(3)加厚合金層狀態，即僅存在合金層，但O形環外徑與狀態(1)保持相同，d=13 mm。

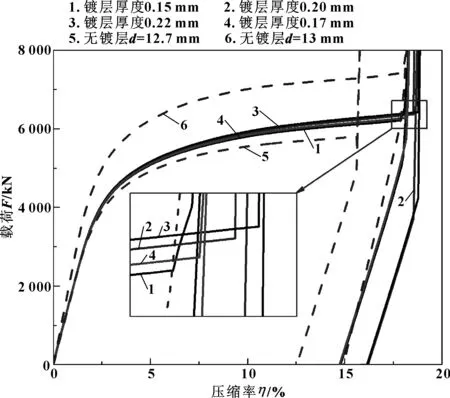
圖7 不同鍍層壓縮回彈特性曲線

比較狀態(1)與狀態(2)，在加載階段，二者壓縮回彈曲線非常接近，失去銀層的O形環在相同壓縮率下由于外徑減小，因此上法蘭位移更大，上下法蘭更早接觸，壓縮回彈曲線更早進入法蘭接觸區。因此，O形環的結構剛度主要取決于合金層，相同的合金層厚度下，鍍層有無對壓縮回彈曲線的總體趨勢影響不大。同時比較狀態(1)與狀態(3)也可以看出同樣規律。

圖8中比較的是狀態(1)與狀態(3)不同壓縮率下對應的接觸壓力分布。可以發現狀態(1)與狀態(3)各自接觸壓力分布隨壓縮率的變化趨勢相同，狀態(1)與狀態(3)具有相似的接觸壓力分布變化規律，鍍銀層對該規律基本無影響。但是在相同壓縮率下，無鍍銀層的O形環其接觸壓力峰值更高，接觸壓力分布在峰值附近更為集中。這是因為鍍銀層材料較合金層更易發生形變，材料塑性更好，對于接觸壓力的分布起到了均化的作用，增大了接觸寬度，更好地填補了泄漏通道，利于形成密封。

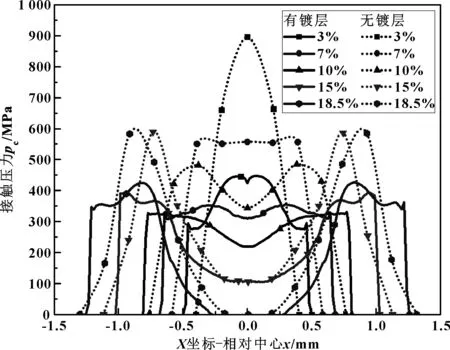
圖8 有無鍍層O形環加載時接觸壓力分布(外徑d=13 mm)

4 結論

(1)建立金屬O形環的平面二維軸對稱有限元模型，仿真得到的壓縮回彈特性與試驗結果具有良好一致性，表明該有限元模型可用于O形環力學性能的分析。

(2)利用該有限元模型進行了O形環力學性能的分析，包括接觸特性、應變特性及壓縮回彈特性。分析結果表明：O形環接觸壓力分布與壓縮率有關，壓縮率過大或過小都將導致密封性能下降；整個壓縮回彈過程可分為彈性變形、塑性變形、法蘭接觸及回彈4個階段，O形環的回彈補償性能由其壓縮率決定。

(3)討論了O形環表面鍍銀層對于其力學特性的影響，表明鍍銀層主要對O形環密封的接觸壓力分布起均化作用，而對O形環總體的壓縮回彈特性影響不大。

(4)建立的模型和分析方法可用于其他法蘭墊片密封系統的力學特性研究。