單比特相關器在超聲測距中的應用研究

張博軒，趙天白

(中國電子科技集團公司第五十四研究所，河北 石家莊 050081)

0 引言

近年來，隨著數字信號處理技術的發展，基于Delta-sigma ADC的單比特信號處理方法開始得到一些應用[1]。傳統的信號時延估計方法，通常需要大量高精度、高分辨率、實時的環境識別，但是每個傳感器的計算能力是有限的，而且在相關的計算過程中需要復雜的數字器件。目前基于Delta-sigma調制的單比特信號處理方法在文獻中已經有所提及，但是還沒有形成比較完善的檢測系統[2]，本文提出一種將單比特信號處理技術應用在硬件系統上的新思路，利用基于Delta-sigma調制器結構的單比特信號處理算法降低FPGA等邏輯芯片計算資源的消耗，實現了單比特信號處理算法從仿真到硬件實現的理論論證。

1 超聲測量的基本原理

1.1 亮點模型

亮點模型最早由湯渭林提出，用于分析主動聲納系統中的目標回波結構，并用來仿真目標回波，同樣也適用于超聲測量中障礙物的回波建模。

理論分析和實驗研究都證明，在高頻情況下，任何一個復雜目標的回波都是由若干個子回波迭加而成，每個子回波可以看作是從某個散射點發出的波，這個散射點就是亮點，它可以是真實的亮點。也可以是某個等效的亮點這樣，任何一個復雜目標都可以等效成若干個散射亮點的組合，每個散射亮點產生一個亮點回波，總回波是這些亮點回波相干迭加的結果。

亮點及其回波具有以下特點，根據形成機理可以把亮點分成2類：

(1)幾何類亮點。它主要由目標的幾何形狀決定，最重要的是凸光滑表面上的鏡反射亮點，當表面曲率半徑較大時，它的貢獻往往是第一位的；其次是邊緣或棱角的反射亮點，有時候它們也不能被忽略。這類亮點回波可以用物理聲學或幾何聲學方法找出，它們的聲中心與幾何中心一致。

(2)彈性類亮點。它們是在特定條件下出現的表面繞行波或彈性散射波對應的亮點。這類亮點必須用波動或幾何繞射理論分析，并不存在真實的幾何亮點，而是根據波傳播的聲程確定的等效亮點。例如，彈性球或球殼的回波是一個脈沖串，其中第一個是鏡反射波，亮點是球的頂點，后續的波都是彈性類散射波，并無真實的幾何亮點存在，但是可以根據這些波相對于鏡反射波的時延值確定等效亮點位置。

超聲測距系統示意如圖1所示。

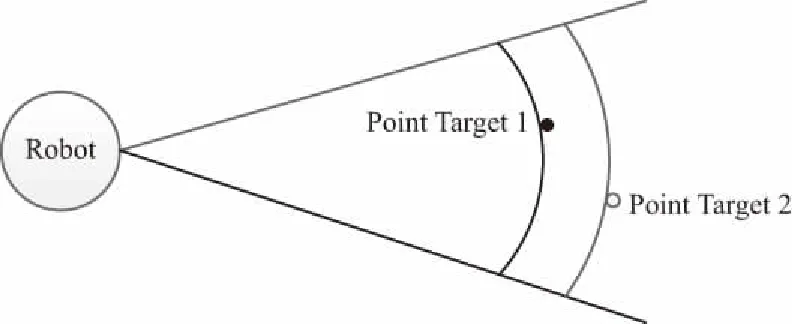
圖1 超聲測距系統示意

考慮如圖1所示的超聲測距系統：超聲傳感器安裝在機器人身體前方，通過周期性發射脈沖信號來探測障礙物距離。最簡單的情況是只有一個亮點的點目標，如果發射的聲信號為s(t)，遇到點目標時發生反射，反射波被超聲換能器接收，接收信號x(t)可以表示為：

x(t)=B·As(t-τ)+n(t)，

(1)

式中，B為超聲波在空氣中傳播的幅度衰減；A為點目標的反射系數，許多情況下，A都是一個復數，A的模值表示反射波的幅度變化，介于0～1之間，而A的輻角表示反射波的相位變化，介于0～2π之間；τ為反射波相對于發射波的時間延遲，超聲測量的目的是估計τ的值，來計算目標的距離；n(t)為接收的噪聲包含環境噪聲和電路的噪聲。

當目標不是一個點目標時，可以根據亮點模型將其分解為M個亮點的組合，這時回波將是M個亮點的回波疊加，接收信號x(t)可以表示為：

(2)

式中，Bi為第i個亮點的傳播損失；Ai為反射系數；τi為時間延遲。M個亮點共同決定了反射波的結構。

1.2 超聲傳感器的波束寬度與分辨率

實際應用中的超聲傳感器具有一定的指向性，實際發射的聲波并不是一根線，而是具有一定寬度的波束。圖2中用兩條射線表示超聲傳感器的波束寬度，圓弧表示傳播時間相同的點，也稱為波陣面，在同一波陣面上的點目標表現為一個亮點，在時間上不能分辨。

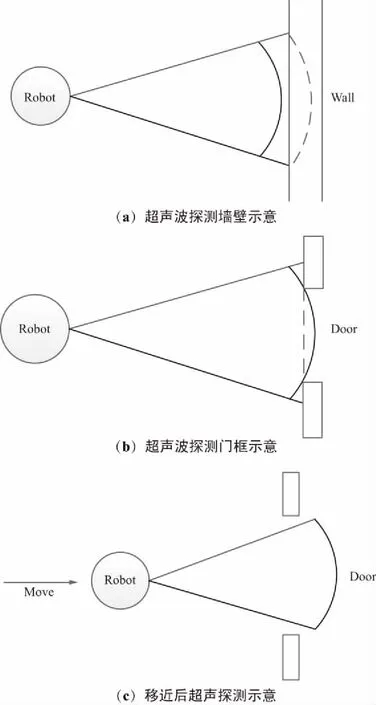
圖2 機器人的超聲測距示意

隨著超聲波的傳播，波陣面將不斷擴大，不能分辨的空間也變大，因此用超聲波探測的距離是有限的。對于一個開角為30°的超聲傳感器，在1 m處不能分辨的距離約為0.52 m，此處將會擴大一倍。

除了同一波陣面上的亮點不能分辨之外，由于反射波時延的測量也不能無限精確，在時延測量精度內的亮點也不能分辨。圖2(a)是用超聲波探測墻壁的情形，這時墻壁上的點由于處于不同的波陣面上，將會形成一連串的亮點，當距離墻壁很近時，這些亮點將會合成一個，從而不能分辨，這其實是許多超聲測距系統的工作狀態。

圖2(b)是測距系統測量門框時的情況，一方面2個門框處于同一波陣面上；另一方面門框的棱角將會形成強的亮點，超聲傳感器接收到門框的回波時，同樣會認為是一道墻(圖2(b)中的虛線所示)，這也是文獻[4]所提出問題的答案。

改善超聲測距系統的分辨能力有2種方法：

① 改善角度分辨能力。可以使用開角更小的超聲傳感器或傳感器陣列，但這意味著如果要探測360°的目標就需要更多的超聲傳感器，更多的時間和成本。同時也可以使用讓機器人運動的方式，一方面，可以通過變換測量位置進行多次測量后將結果綜合后進行判斷[5]；另一方面可以通過運動讓門的距離更近些，如圖2(c)的情況。光學探測的情況略有不同，還可以使用放大鏡和望遠鏡這些光學聚焦手段。

② 改善時間分辨能力。如果能夠精確地測量門框和墻壁的位置，自然也能判斷出是門還是墻壁。

1.3 匹配濾波與脈沖壓縮

接收到的信號除了亮點的反射波，還包含隨機噪聲n(t)，通常假設是白噪聲，具有平坦的功率譜密度N0。根據最大輸出信噪比準則，可以得到最佳的檢測器為[6]：

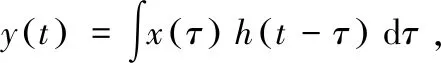
(3)

式中，

h(t)=Ks*(t0-t)，

(4)

為檢測器的沖激響應；K為一個常數；t0為對參考信號s(t)時延時刻，這一系統被稱為匹配濾波器。把式(4)代入式(3)可得：

(5)

其輸出實際是接收信號與發射信號互相關函數RXS，因此匹配濾波器與互相關器是等價的。

進一步將式(1)代入式(5)中可以得到匹配濾波器將在t=t0+τ時刻具有最大輸出信噪比：

(6)

如果定義輸出信噪比與輸入信噪比的比值為處理增益：

(7)

式中，B為接收系統的帶寬，一般與信號的帶寬相同；T為信號的脈沖寬度。

對于頻率為f0的單頻脈沖信號，

(8)

其帶寬B和脈沖寬度T近似滿足[7]：

BT≈1。

(9)

也就是說，如果使用單頻脈沖信號進行檢測，其獲得的處理增益G將是一個常數。

對于功率為P，TB=N>1的復雜信號，其脈沖長度為T，經匹配濾波器后其輸出脈沖寬度為：

(10)

輸出脈沖峰值功率是P0，并近似有：

P0T0=PT。

(11)

因此，

P0≈NP。

(12)

一方面匹配濾波器將信號長度由T壓縮到T0=T/N；另一方信號功率由P增加到P0。這就是“脈沖壓縮”的含義，N=TB就是脈沖壓縮倍數。顯然，一切TB>1的信號都是脈沖壓縮信號，獲得的處理增益G將大于單頻脈沖信號。最常用的復雜信號有線性調頻信號(LFM信號)，其表達式為：

(13)

式中，f0為線性調頻信號的起始頻率；k=B/T為調頻率。

1.4 模糊度函數與分辨率

信號s(t)的模糊函數定義為[8]：

(14)

對于式(3)定義的匹配濾波器而言，如果輸入的信號是有時延τ0和頻移ξ0時，

x(t)=s(t-τ0)ej2πξ0(t-τ0)。

(15)

其輸出變化為：

y(t)=Kχ(τ0+t0-t，-ξ0)。

(16)

因而，通過研究信號模糊函數的特性可以了解聲吶系統匹配濾波處理的效果，而這正是模糊函數研究的最大意義。

假設有2個亮點的反射波信號：亮點1反射波時延為τ0頻移為ξ0。亮點2的回波時延τ0-τ頻移為ξ0+ξ，即

x1(t)=s(t-τ0)ej2πξ0(t-τ0)，

(17)

x2(t)=s(t-τ0+τ)ej2π(ξ0+ξ)(t-τ0+τ)。

(18)

可以采用2個信號的方差即

(19)

來衡量2個信號的差別，σ2越大越容易區分這2個目標的回波。將式(17)、(18)代入式(19)式可得：

δ2≥2[E-|χ(τ，ξ)|]。

(20)

因此，模糊度函數也用來分析信號的分辨能力，如果目標不運動時，亮點的反射波沒有頻移項ξ0，可以用模糊度函數在時延軸上的剖面χ(τ，0)來衡量信號的時間分辨率，如果以|χ(τ，0)|幅值的0.707作為分辨2個目標的極限值，對應的延時寬度Δτ就是信號的時間分辨率。

根據式(6)，匹配濾波器檢測增益的提高只能依靠增加信號的能量，而與信號形式無關，同樣能量的信號，單頻長脈沖和復雜信號具有同樣的檢測效果。但是，單頻脈沖信號能量的增加主要靠增加功率P或信號長度T。增加峰值功率受到發射系統和傳感器最大功率的限制，因此一般靠增加T來增加信號能量。但單脈沖T的增加，意味著信號帶寬B的減小，因此距離分辨力也減小。如果要求匹配濾波在不降低信號距離分辨性能的條件下，提高檢測性能，必須采用復雜信號。

圖3顯示了CW和LFM信號探測能力的對比。有6個亮點分別位于距離超聲傳感器1，1.006，1.03,1.05，1.07，1.09 m處，忽略空氣中的傳播損失，前4個亮點的反射系數均為0.2，后2個亮點的反射系數為0.05，接收系統的帶寬為20 kHz，噪聲是功率為1 W的白噪聲，圖3(a)，圖3(b)分別是發射脈寬為50 μs的CW和LFM的信號時，互相關器的輸出，可以看出，由于前2個亮點的距離差小于發射信號的最小分辨率，其輸出的峰值靠得很近，較難分辨，中間2個亮點的回波則能夠清楚地區分開，最后2個亮點由于信噪比不夠高，已經不能分辨。圖3(c)，圖3(d)是將發射脈寬加長至400 μs時的輸出，由于發射信號能量的增強，輸出的信噪比明顯增加，圖3(d)中最后2個亮點已經清晰可辨，而圖3(c)由于使用CW脈沖，其時間分辨率降低，6個亮點已經不能分辨。

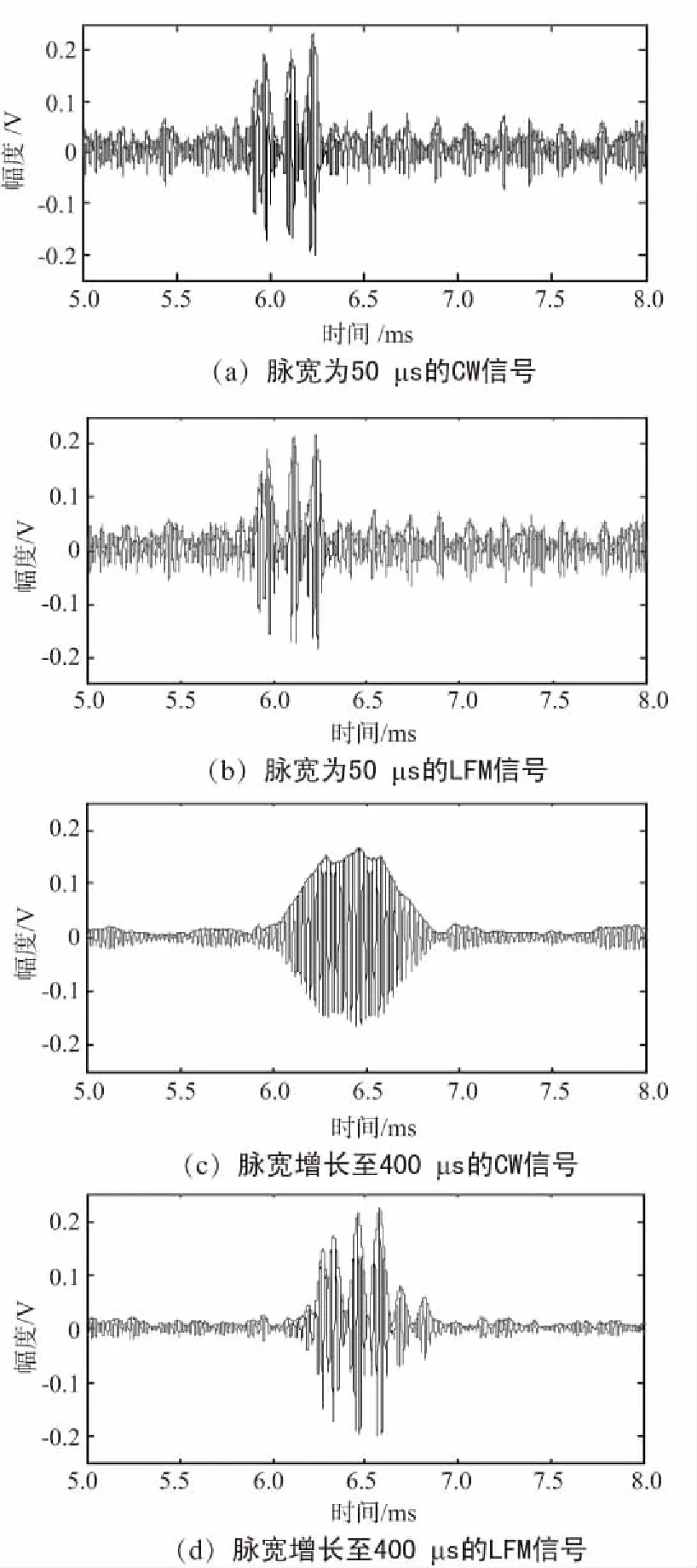
圖3 互相關器的輸出

1.5 相位匹配與失配

式(3)所定義的匹配濾波器是復數運算的，而實際使用中的信號都是實信號xI(t)，為得到其虛部xQ(t)，需要進行希爾伯特變換：

xQ(t)=Hilbert[xI(t)]，

(21)

x(t)=xI(t)+jxQ(t)。

(22)

進行匹配濾波后再取輸出的實部進行判斷：

yI(t)=Re[y(t)]=K·Re[Rxs(t0-t)]。

(23)

亮點的反射系數是一個復數A=|A|ejφ，此時回波信號是：

x(t)=|A|ejφs(t-τ)。

(24)

將式(24)代入式(23)中得到匹配濾波器輸出：

yI(t)=Re[Rs(t0+τ-t)ejφ]，

(25)

式中，Rs(t)是信號的自相關函數。

t=t0+τ時，輸出變為：

yI(t)=Rs(0)cosφ。

(26)

可見，除非φ=0，否則yI(t)不可能達到最大輸出值Rs(0)。由于在檢測中，相位并不包含所需要的信息，因此，通常取復相關或匹配濾波運算輸出的模為：

|y(t)|=|Rs(t0+τ-t)|，

它與φ無關，完全匹配時，

|y(t)|=R0(0)=E，

計算方法為：

(27)

式中，

(28)

式(27)，(28)也被稱為正交接收機，為了避免計算輸入信號xI(t)的希爾伯特變換xQ(t)，還可以使用：

(29)

聯合式(27)來計算，值得注意的是就信噪比檢測增益而言，式(28)，(29)定義的匹配濾波器都要比相位完全匹配的匹配濾波器小3 dB。

2 單比特相關器

2.1 數字相關器

隨著超大規模集成電路(VLSI)的發展，使用基于集成電路的數字信號處理方法進行計算具有更高的通用價值[9]。根據數字信號處理的基本理論，可以將式(27)，(29)分別表示為其采樣形式：

(30)

(31)

可以將反射回波信號經過AD采樣量化后用大規模集成電路進行數字計算[10]。

2.2 Delta-sigma調制

Delta-sigma AD轉換器是近年來發展的一種新型結構的AD變換器[11]，與傳統的AD變換器不同，借助于過采樣技術，可以用較少的比特數來表示被采樣信號，在音頻信號領域得到廣泛應用。圖4(a)是一階單比特Delta-sigma調制原理圖。輸入的模擬信號經過單比特量化ADC(比較器)量化為1 bit的數字信號，比較器的輸出再使用一個單比特DA轉換器轉換為模擬信號，并與輸入信號進行相減，其輸出端輸出1就表示當前輸入的模擬信號比前一時刻的信號增加，而輸出-1則表示比前一時刻減小。圖4(b)顯示了單比特Delta-sigma調制器量化正弦波的例子，如果輸入電平是一個固定的直流電平時，調制器的輸出端會在1和-1中交替變化。

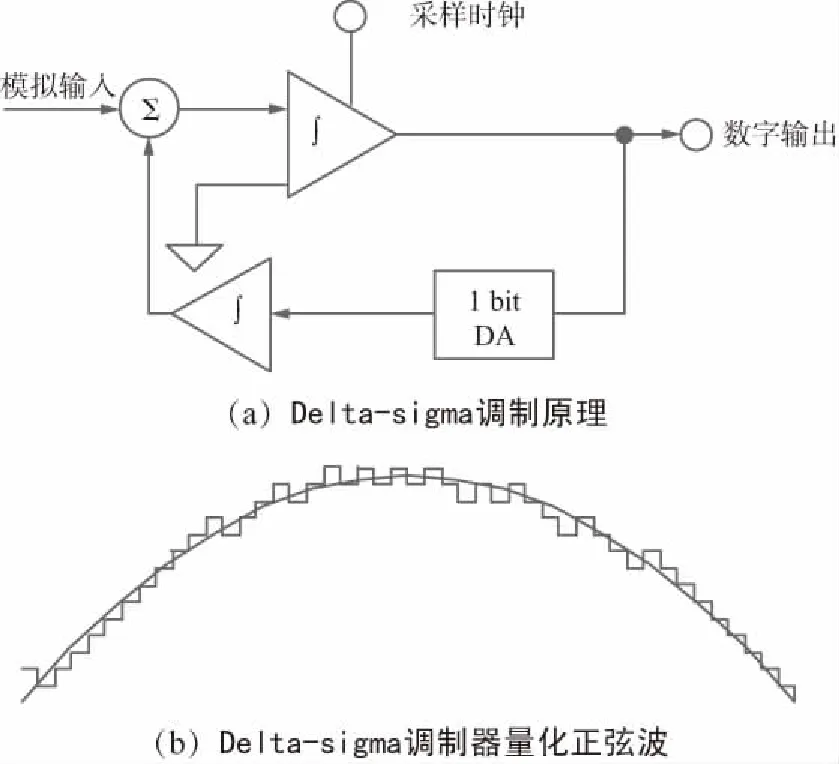
圖4 Delta-sigma調制

對于傳統AD轉換器來說，當采樣速率高于兩倍的信號最高頻率時，可以無失真地回復原信號。這就是奈奎斯特采樣定律，而使用Delta-sigma調制器進行采樣時，采樣的量化噪聲不是均勻分布在整個帶寬內的，距離其采樣頻率越近的頻率點量化噪聲越高，為了降低量化噪聲的影響，Delta-sigma調制器的采樣速率需要遠高于信號的奈奎斯特采樣頻率，即過采樣技術，再借助于帶限于奈奎斯特采樣頻率的數字低通濾波器來濾除量化噪聲的影響。

2.3 單比特相關器

借助于Delta-sigma調制器，可以將復雜的信號表示為單比特的數字信號，在后序的數字信號處理中，減小了計算的復雜度。Mirioru等人最早將單比特信號處理技術應用于直流電機的控制中[12]，而后Shinnosuke和Mirioru設計了單比特互相關器，并將其用于機器人超聲測距中[13-14]。

文獻[12]中給出了單比特相關的計算方法，應用其推導結果，互相關器2個相鄰時刻輸出差表示為：

y1(t)-y1(t-1)=-x1(t-N)+2x1(t-N+Z1)。

(32)

可以經由Delta-sigma調制的輸入信號，同樣計算得到調制后的相關函數，再由：

y(t)=y1(t)+y1(t-1)，

(33)

即可還原出相關函數，計算出的結果還要經過低通濾波，濾除高頻量化噪聲。

同理可以得出進行復數運算時，只需要分別將參考信號的實部和虛部分別進行單比特互相關運算，再求模值即可，具體計算流程如圖5所示。

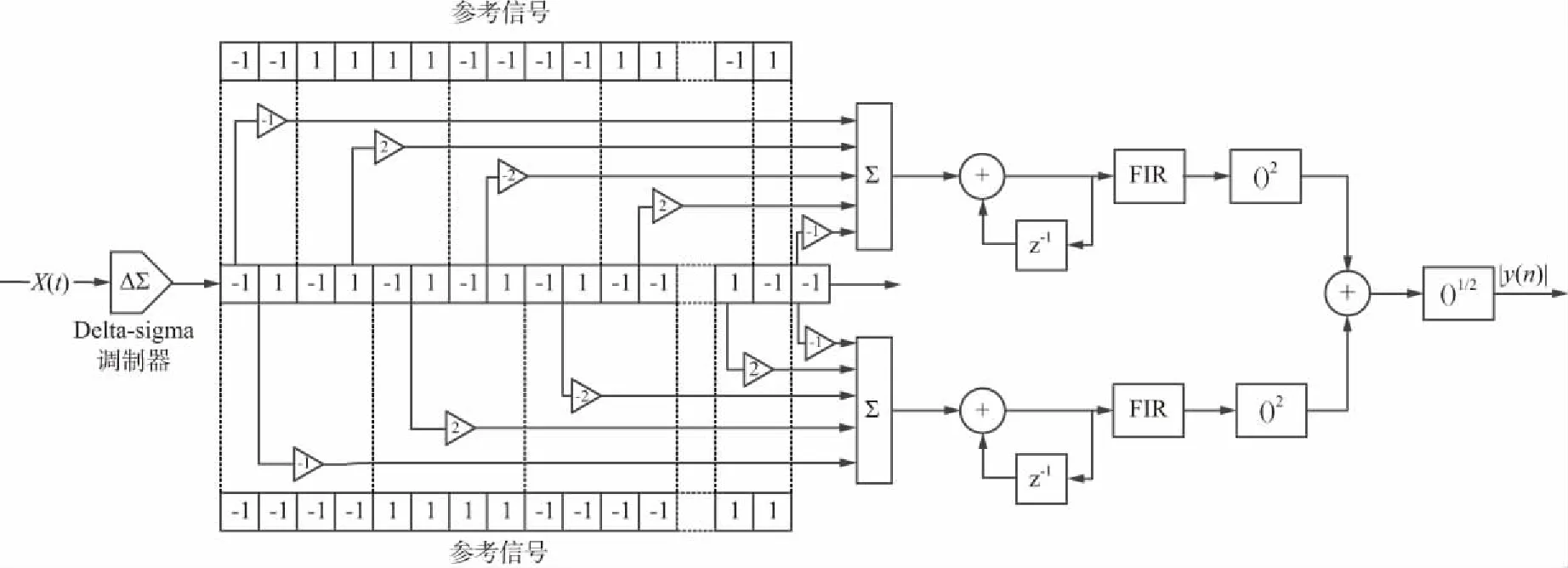
圖5 單比特互相關器計算流程

這種單比特相關器大大減小了相關運算的復雜度，只需要使用M個累加器和較少位數的乘法器，特別適用于FPGA/CPLD或專用ASIC實現。

3 仿真實例

仿真實驗是用Matlab計算完成。發射選用線性調頻脈沖LFM信號，脈寬為5 ms，6個點目標分別位于1，1.006，1.03，1.05，1.07，1.09 m處，其反射系數的模值均為0.2，前4個亮點相移為0，第5個亮點相移為180，第6個亮點相移為90。空氣中的聲速取340 m/s。接收信號使用單比特一階Delta-sigma調制器進行調制。調制器的采樣速率為12.5 MHz，輸出FIR濾波器采用119步的三角加權滑動平均以濾除量化噪聲。為了對比，同時用Matlab以采樣速率125 kHz進行相關運算，無環境噪聲時計算結果如圖6所示。

圖6(a)是Matlab浮點互相關器的計算結果，計算采用復數運算，實線是式(23)的計算結果，是互相關器輸出的實部，虛線是式(27)，(28)的計算結果，是互相關函數的模值，圖6(b)是單比特互相關器計算的結果，圖6(c)是上述方法中的單比特相關器的計算結果，從圖6中可以看出，應用單比特互相關器計算的互相關函數是與Matlab的浮點計算結果是相符的，包絡計算對應每個亮點的位置都有與之相對應的單個峰值，而實數計算則有多個峰值，正確判斷峰值的位置需要比較復雜的算法，在實際應用中不如包絡計算使用方便。測量的分辨率與信號的分辨率是不同的，測量分辨率是指應用測量方法(例如最大值檢測)能夠分辨的最小單位，一般與采樣精度有關，而信號的分辨率則是第二節中由模糊度函數來定義的兩個相鄰亮點的最小分辨距離，具體的例子是應用單比特相關器在12.5 MHz采樣率的情況下能分辨的最小距離約0.013 6 mm，而帶寬20 kHz的LFM信號的最小距離分辨率約為7.48 mm，實際測量系統的分辨率是二者中間較小的那個。

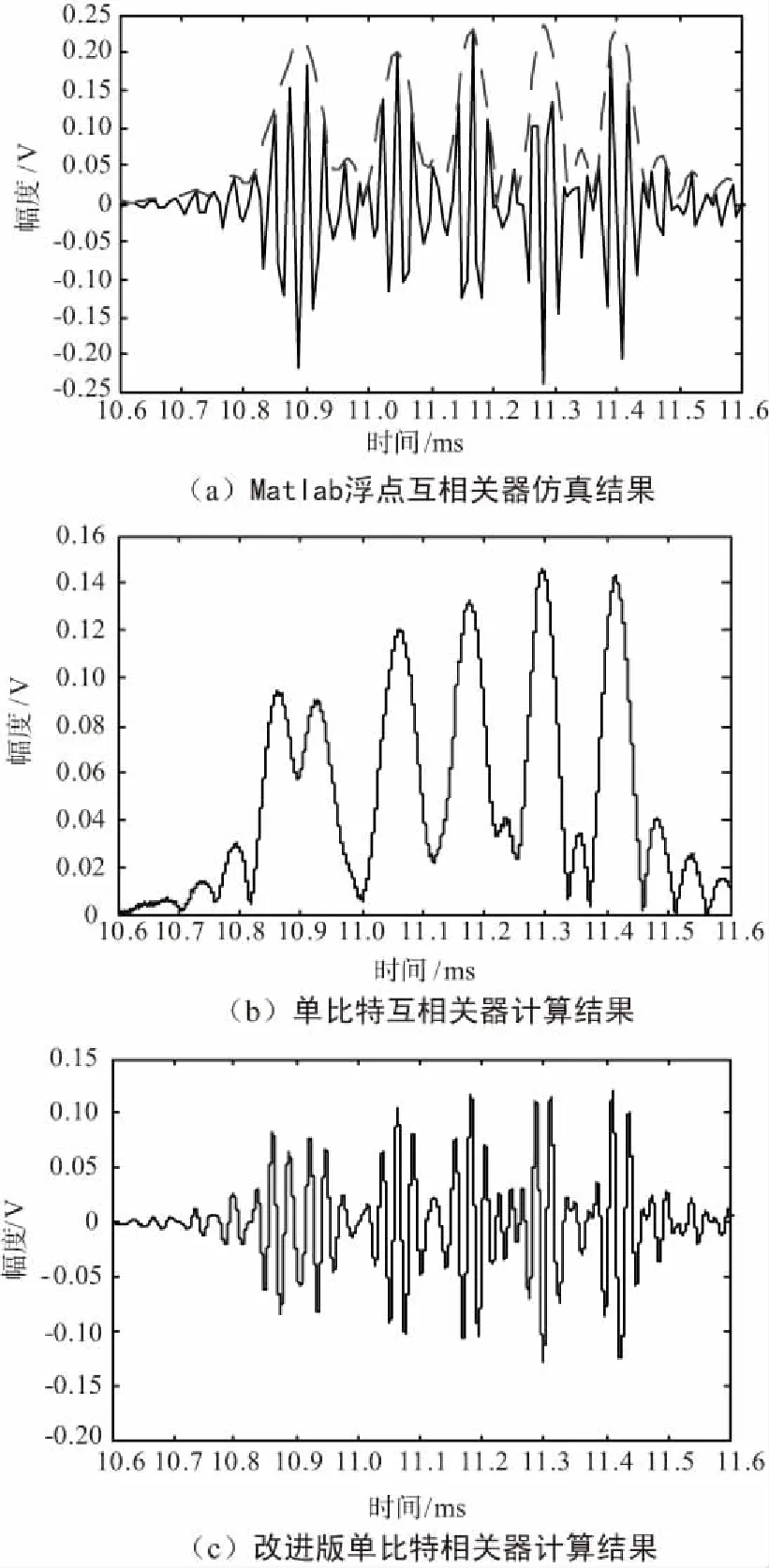
圖6 互相關器仿真計算結果

4 結束語

根據信號的模糊度函數可以得出超聲測距系統的最小距離分辨率是其帶寬決定的，測距的分辨率不能任意小。通過計算機仿真證明，基于Delta-sigma調制器的單比特互相關器的超聲波測距系統可以獲得比傳統互相關器更高的精度，用互相關器輸出的包絡值代替實值進行距離測量可以補償回波相位失配帶來的影響，在較小的精度損失下可以使超聲測距系統具有更高的魯棒性，提高機器人對環境的適應能力，為形成基于Delta-sigma調制的單比特信號處理系統提供了一定的理論基礎和應用依據。