基于尺寸優化的水輪發電機上機架輕量化設計

廖永宜，廖伯瑜

(1.昆明理工大學云南省高校振動與噪聲重點實驗室，云南昆明650500；2.昆明理工大學成人教育學院，云南昆明650051)

0 引 言

上機架是水輪發電機的主要承載部件，其設計直接影響機組的整體性能。上機架的尺寸較大，形狀復雜，在其結構設計中，除滿足它的各種功效外，還應在保證其強度、剛度和動力特性要求下，實現結構輕量化優化。隨著水輪發電機單機容量的提高，機組尺寸的增加，結構輕量化要求更顯突出[1-2]。

對水輪機及其相應零部件的結構優化設計和動態特性分析已取得了一些研究進展[3，4]。結構優化設計方面，主要是對相應零部件形狀、強度、剛度進行性能優化和改進設計。王波等[5]通過有限元法對水輪機水斗高應力區進行結構尺寸的優化，優化后的方案滿足強度和結構水力性能要求，并研制了水斗加工用大長徑比減振刀柄，以保證制造精度。邵國輝等[6]對水輪機的蝸殼、尾水管、轉輪等水力過流部件進行改型優化設計，分析結果與試驗數值基本滿足水力設計參數要求。齊學義等[7]對水輪機頂蓋分別運用傳統機械設計方法和機械可靠性設計方法進行了計算，并給出了兩種計算結果的比較分析。動態特性方面，主要分析結構固有頻率與振型，通過提高結構低階固有頻率以避開激勵頻率，抑制結構共振[8]。姚大坤等[9]用錘擊法和變時基技術對水輪發電機上機架動力特性進行試驗研究，提出了上機架薄弱部位的加固方案。袁曉明等[10]通過建立水輪發電機上機架、定子和轉子的耦合模型，對模型固有頻率、振型和諧響應進行了分析，得出上機架肋板和千斤頂剛度對振動幅值的影響規律。李兆軍等應用有限元法，以混流式水輪機為研究對象，建立轉輪葉片的動力學方程并求出葉片的固有頻率，并推導了轉輪葉片的共振失效概率[11]；通過建立主軸系統非線性動力學方程，提出多失效模式水輪機非線性振動分析方法[12]。

上述研究關注于水輪發電機零部件性能優化設計和動態性能分析，對于輕量化目標的優化設計相對較少。本文以某電機廠混流式水輪發電機上機架為研究對象，根據上機架的實際尺寸和工況，建立上機架有限元模型，對其動力特性進行仿真分析，基于結構尺寸優化設計方法，以結構板厚為設計變量，以正應力和剛度兩種設計指標為約束條件，采用復合形法尋優迭代，對上機架進行以質量最小為目標的優化設計。

1 結構尺寸優化設計方法

結構優化是指如何找到一種由設計變量決定的合適的結構，在實現結構功能要求的情況下，滿足某些方面的性能為最優，如質量最小、剛度最大、動態特性能最好等[13]。這種最大或最小是以約束條件來限制的，如應力、位移和幾何形狀等。通常選取可以最大化或最小化的某些參數作為優化目標函數，而其他參數作為約束。設計變量表示結構的某種幾何特征，根據幾何特征的不同，結構優化問題一般分為三類，即尺寸優化、形狀優化和拓撲優化[14]。尺寸優化的設計變量為結構某種類型的尺寸(如橫截面積，板厚等)；形狀優化的設計變量代表設計域的形狀或輪廓，采用一組偏微分方程描述其狀態；拓撲優化是結構優化的高級形式，其設計變量具有更大的設計空間和更多的自由度，目前還處于初級研究階段[15]，其主要困難在于實現結構功能要求的結構有無窮多種形式，并且這些拓撲形式難以定量描述即參數化，限制了拓撲優化建模和求解的實際應用。形狀優化由于涉及結構邊界的復雜數學描述，在實際結構的優化設計中應用還不多[15]。

尺寸優化涉及的是結構參數的控制，在結構改進設計和輕量化設計中通常可以得出較為具體和便于應用的結論，實用性強，適合工程應用。

1.1 尺寸優化設計的數學模型

在尺寸優化設計中，一般為約束優化設計問題，其數學模型可表示為

(1)

設計變量x定義為n維歐氏空間的一個列向量，該空間包含了設計中所有可能的方案，每一個設計方案對應設計空間上的一個設計向量或者一個設計點x。設計變量是獨立影響設計目標的某種類型的尺寸，如結構的截面積、厚度和長度等。

目標函數f(x)用于衡量設計的優劣，其選擇原則是函數值最小，即minf(x)。通常尺寸優化設計中目標函數用于評價結構質量、給定方向的位移、振幅、應力或成本等，可以是單目標函數或多目標函數，對應的即為單目標優化問題或多目標優化問題[16]。

尺寸優化設計中設計變量的取值范圍是通過約束條件來限制的，約束條件是包含設計變量的函數，可用i個等式或j個不等式描述，即hi(x)=0或gj(x)≤0。約束一般可分為幾何約束(或稱邊界約束，如長度、截面積等)和性能約束(如工作應力小于許用應力等)。

1.2 約束優化問題的解法

約束優化問題的求解方法可以歸納為：尋求一組設計變量x=[x1,x2,…,xn]T，在滿足約束條件hi(x)=0和gj(x)≤0的條件下，使目標函數f(x)最小。其求解方法分為間接解法和直接解法。

間接解法用于求解同時存在不等式約束和等式約束的優化問題，其基本思路是：將一個約束優化求解問題轉化為求無約束優化的極值問題， 再采用無約束優化方法求解。 屬于間接法求解約束優化問題的方法主要有：消元法、拉格朗日乘子法和懲罰函數法等。

直接解法主要用于求解含有不等式約束的優化問題，或者當等式約束不是復雜的隱函數且消元過程容易實現時，也可使用直接解法。其基本思路是：在約束條件所確定的可行域內選擇一個初始點x0，按可行搜索方向以適當的步長進行搜索，得到一個使目標函數值下降的可行的新點x1，即完成一次迭代。再以新點為起點，重復上述搜索過程，滿足收斂條件后，迭代終止。直接解法原理簡明，方法實用，若目標函數為凸函數，可行域為凸集，則可保證獲得全域最優解；否則，因存在多個局部最優解，當選擇的初始點不同時，可能搜索到不同的局部最優解，需要在可行域內選擇若干個差別較大的初始點分別進行計算，從中選擇更好的最優解。屬于直接解法的主要有復合形法、隨機方向搜索法和可行方向法。

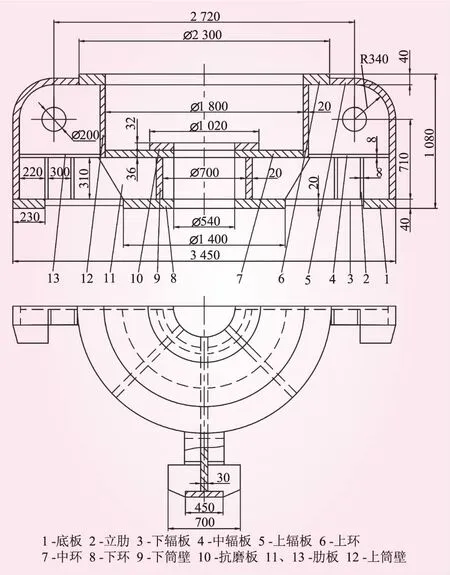
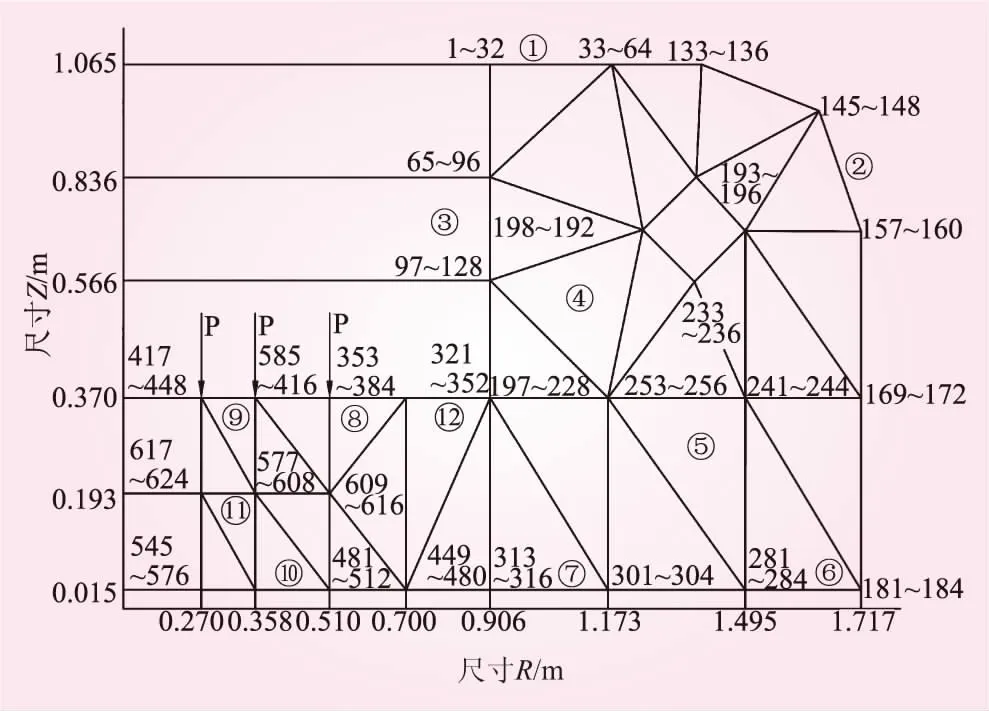
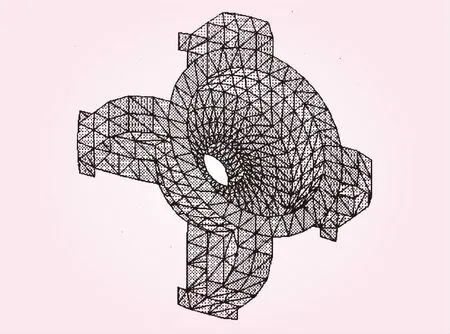
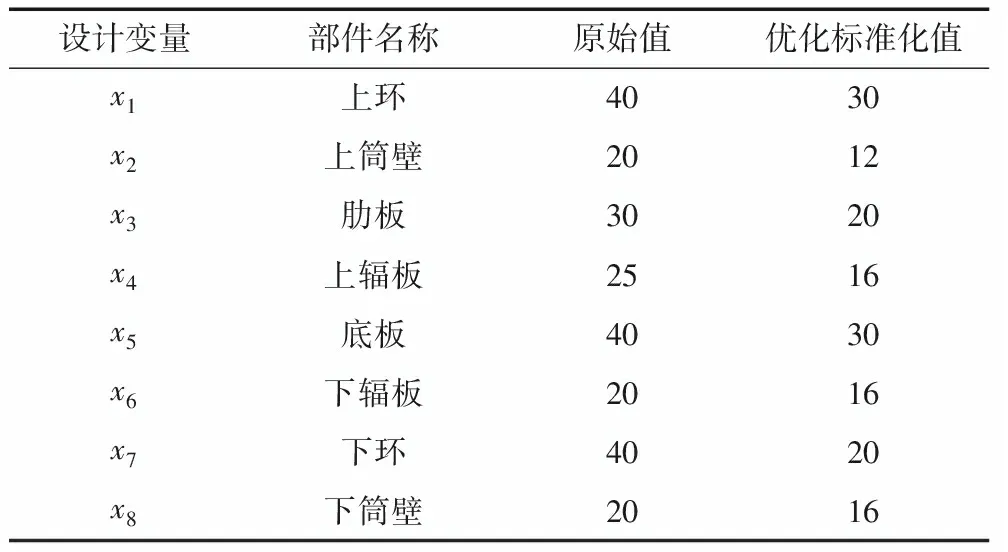
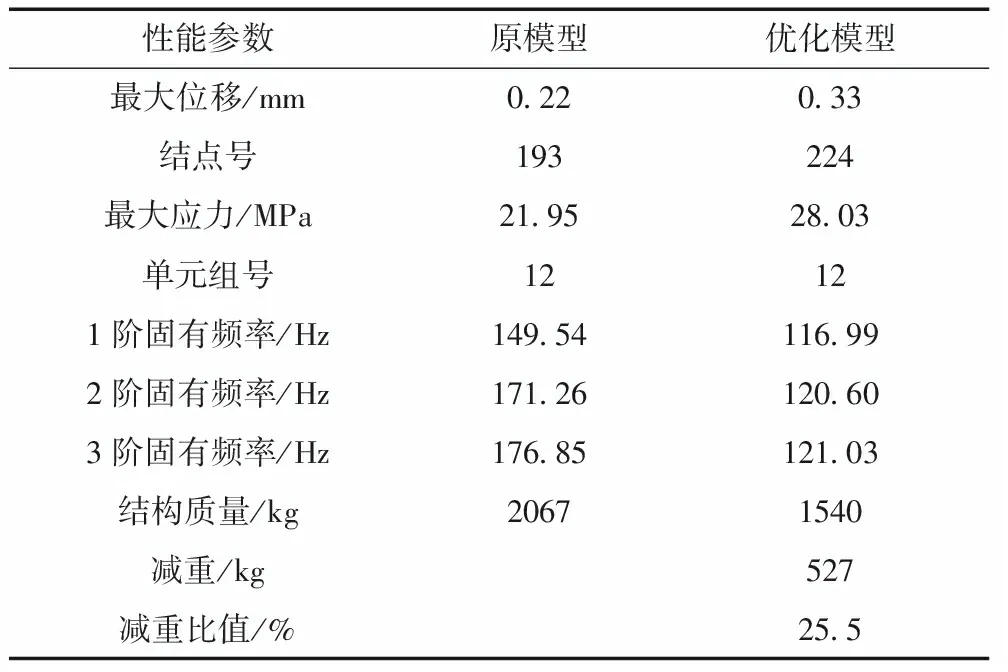
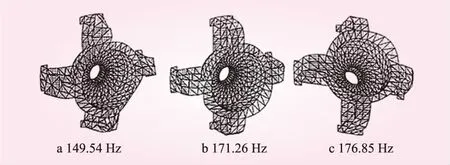
復合形法由單純形法發展而來，它克服了單純形法容易出現的降維現象，其基本思路是在可行域內構造一個具有k個頂點的初始復合形(對于n維設計問題，n+1

2 上機架有限元模型與等效荷載計算

上機架結構簡圖如圖1所示，主要由上環、中環、下環、筒壁、輻板、肋板和底板等構成。

圖1 上機架結構示意(單位：mm)

上機架采用厚度不等的碳素結構鋼板材制成，為板式箱體復雜結構。由于三維三角形板殼單元可以較精確地劃分復雜的三維結構，它由平面應力膜單元和平板彎曲單元組合而成，因而可以傳遞彎曲和剪切力，這種力學特性更接近上機架的受力狀況。因此，采用三維三角形板殼單元作為上機架結構有限元模型的單元元素。上機架結構有限元離散模型如圖2所示，整個上機架有限元模型包含870個單元，440個結點，2 640個自由度。其有限元模型如圖3所示。

圖2 上機架有限元離散模型

圖3 上機架有限元模型

上機架是發電機組中的主要受力部件，通過四個對稱分布的支臂底板用銷軸和螺栓固定在發電機機座上，支臂的底板為固定約束面。發電機轉動部分的自重及軸向推力通過推力軸承全部作用于上機架耐磨板上。發電機軸線安裝偏差或轉動部分質量偏心還將引起不平衡力，并通過上導軸承沿徑向作用于上機架，不平衡力在機組遠離固有頻率正常運行時一般很小，故在計算上機架荷載時，僅考慮正常工況下發電機轉子的止推端作用在耐磨板上的荷載668 kN，采用等效的方法將荷載均勻分布在耐磨板的96個節點上，每個節點的荷載取為7 kN。

3 上機架輕量化設計的數學模型

由于上機架的整體結構尺寸如安裝尺寸和配合尺寸等不能改動，在發電機上機架輕量化設計中，基于尺寸優化方法，選擇上機架結構的8種板厚為設計變量，記為

X=[x1,x2,…,x8]T

(2)

將發電機上機架質量W(X)作為優化設計的目標函數，由除板厚以外的結構尺寸建立其表達式。以滿足上機架結構有限元平衡方程以及強度和剛度條件作為約束條件，具體為結構各單元組的最大應力和結點的最大位移均小于許用值，即

(3)

式中，[σi]是第i個單元組的許用應力值；[δj]是第j個結點的許用位移值。

則得到下機架輕量化優化設計的數學模型為

(4)

4 上機架輕量化設計結果及對比分析

根據上機架輕量化設計的數學模型，以輕量化設計為目標，以滿足上機架最大正應力和剛度條件為約束條件，對上機架進行分析計算，采用復合形法進行尋優迭代，將最優值圓整為標準化值，得到發電機上機架優化結果，見表1。

表1 上機架優化設計結果 mm

對上機架原模型和優化模型兩種有限元模型在載荷作用下的最大應力、最大位移、結構前3階固有頻率、模態振型及結構的質量分別進行了仿真分析計算，對比結果列于表2。其對應的振型如圖4、5所示。

原模型最大位移發生在第193結點，最大位移值為δmax=0.22 mm;最大應力發生在第12單元組，其值僅為σmax=21.95 MPa，材料未得到充分利用，有較大的輕量化空間。

表2 上機架原模型和優化模型計算結果比較

圖4 上機架振型(原結構)

圖5 上機架振型(改進結構)

為驗證有限元模型的正確性和有效性，對原結構和優化改進結構分別進行了錘擊脈沖激振試驗，并研制了用于激振的專用力錘。測試數據經信號處理機7T17S分析，識別出上機架的模態參數，其前3階模態頻率和模態振型與模型計算的固有頻率和振型均較好相符，所建立的模型能較好地模擬實際結構。

輕量化設計后發電機上機架的板厚明顯地減小，結構的質量減少了527 kg，減重率達25.5%。上機架的最大應力及最大位移均在許用值范圍內，材料的潛力得到了充分利用。模態分析表明，優化后結構的動態特性均滿足要求。其第1階固有頻率116.99 Hz仍遠高于水輪機組的飛逸頻率16.04 Hz，不會因輕量化設計后產生共振。

輕量化設計改進后的發電機上機架應用于某電站水輪發電機組，運行9個月后，在滿負荷運行狀態下經現場測試，上機架動力特性完全滿足要求，取得較好的經濟效益。

5 結 論

(1)通過建立模擬上機架的有限元模型，以此為基礎上對其進行強度、剛度分析和尺寸優化。

(2)基于結構尺寸優化設計方法，以上機架最大正應力和剛度為約束條件，以輕量化設計為目標，采用復合形法進行尋優迭代，得到發電機上機架優化結果。

(3)優化設計使發電機上機架結構的重量有效減輕，其動力特性均滿足設計和使用要求。優化方法具有較好的實用性，適合工程應用。