任意邊界下多跨梁彎曲計算及其工程應用

熊劍鋒，閆肖杰，江璞玉，劉均，程遠勝*

1華中科技大學船舶與海洋工程學院，湖北武漢430074

2中國艦船研究設計中心船舶振動噪聲重點實驗室，湖北武漢430064

0 引 言

多跨梁模型是船舶、橋梁領域常見的力學模型。目前，國內外針對任意邊界條件下梁結構的振動與沖擊方面的研究較多。例如，文獻［1-3］提出了一種改進的傅里葉級數方法（Improved Fourier Series Method，IFSM），該方法在傳統的余弦傅里葉級數的基礎上，增加了4項正弦級數，是一種半解析法（Semi-Analytical Method，SAM）。經數學證明，此方法可擴展并收斂于任意一個函數，通過對彈性邊界條件下的梁、板的振動分析，驗證了此方法的正確性。Xu和Li［4］則在傳統的傅里葉余弦級數的基礎上添加了4項多項式級數（此方法也可消除傅里葉級數在邊界上的不連續問題），并研究了動載荷下多跨梁響應的問題。此外，周渤和石先杰［5］也利用該級數形式研究了任意邊界條件下多跨梁振動的問題。目前，針對任意邊界條件下梁或多跨梁彎曲的問題，主要采用經典的結構力學法或有限元法（FEM）求解，前者需要先求解三彎矩方程或五彎矩方程，然后再由求得的節點彎矩值得到每跨位移，進而利用其他物理量與位移的微分關系得到待求解的物理量結果，而后者則首先需要在前處理中建立模型，然后再求解，因此整個過程耗時較長，且當幾何參數變化時修改也較麻煩。

在滾裝船和大型艦船中，車輛裝載甲板及機庫甲板上的強橫梁及縱桁等主要承力構件均可被視為一種多跨梁結構，在輪印載荷下，其承受的載荷大小與作用位置具有不確定性。因此，在多種輪印載荷工況下找到多跨梁的最危險工況，對于船舶結構的安全校核及裝載方案的設計具有重要意義。為此，Jeon和Kim［6］研究了遺傳算法應用于最危險工況分析的算法性能，成功找到了多個經典數學問題的最危險工況。方陸鵬等［7］將輪印載荷簡化為集中力，制作了輪印載荷下連續多跨梁結構模型的試驗裝置，并對比了彎矩的理論值與實驗值，結果表明兩者基本一致。康杰豪等［8］采用有限元法與遺傳算法相結合的方法，首先利用有限元法計算多跨梁結構各載荷工況下的響應值，然后結合遺傳算法找到在輪印載荷作用下各跨彎矩或剪力的最大、最危險工況，以此對多跨梁結構進行優化設計。但是有限元法計算較為耗時，而傳統的遺傳算法所需的計算設計點較多，導致總體計算效率不高，且由于輪印載荷作用位置采取的是離散取值，故無法找到更精確的載荷危險作用工況。

鑒于此，本文將利用IFSM方法并基于哈密頓原理，首先推導出任意邊界條件下多跨梁彎曲問題的平衡方程，并結合邊界條件聯立求解，然后通過與有限元計算結果的對比，驗證所提方法的正確性，最后將該方法與處理連續變量優化問題的遺傳算法進一步結合，求解輪印載荷位置處于連續變化情況下多跨梁的最危險工況，以獲得其更精確的布置工況。

1 連續多跨梁彎曲問題理論計算

1.1 物理模型

如圖1所示，假設n跨連續梁第i跨的物理參數為li，Ei，Ii，分別指第i跨的跨長、彈性模量和剖面慣性矩。對于邊界上彈簧的剛度系數，規定如下：k0，K0分別指連續梁的首端位移彈簧及轉角彈簧的剛度系數；kn，Kn分別指連續梁的尾端位移彈簧及轉角彈簧的剛度系數；ki指中間支撐位移彈簧的剛度系數，在其上作用一個任意形式的橫向彎曲載荷q（x）。通過改變各彈簧的剛度系數，即可模擬任意一種邊界條件。例如，當模擬兩端為剛性固定、中間簡支時，僅需將兩端的彈簧剛度系數 (k0，K0，kn，Kn)及中間簡支的彈簧剛度系數ki均設置為無窮大即可，對于模擬自由邊界，僅需將各彈簧的剛度系數設置為0即可。

圖1 任意邊界條件的多跨連續梁模型示意圖Fig.1 Schematic diagram of the multi-span continuous beams model under arbitrary boundary conditions

1.2 模型半解析求解

1.2.1 位移級數的表達形式

對于任意邊界下的連續梁第i跨位移函數，可以由如下 IFSM［2］形式表示：

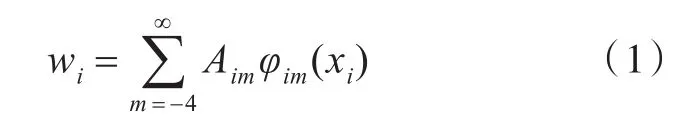
其中，

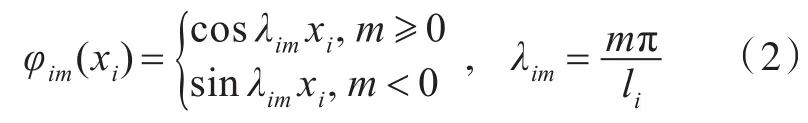
式中：wi為連續梁第i跨的位移；φim為形函數，其中下標m為每項級數的整數序號；Aim為形函數的系數；xi為連續梁第i跨范圍內某個點的位置坐標；li為連續梁第i跨的長度。

上述位移級數形式在傳統的傅里葉余弦級數形式的基礎上，增加了4項傅里葉正弦級數，此形式克服了單一形式的傅里葉級數在邊界上的不連續或跳躍現象。從數學上可知，該級數形式可擴展并收斂于任意一個函數f（x）。在實際計算時，位移級數上限值取為某一正整數M，即級數的截斷數，每個位移wi共包含M+5個未知系數Aim，而求解這n×（M+5）個未知系數則是關鍵。

1.2.2 邊界條件處理

針對圖1所示的n跨連續梁結構，其首端邊界方程可分別由式（3）和式（4）表示，尾端邊界方程可分別由式（5）和式（6）表示：

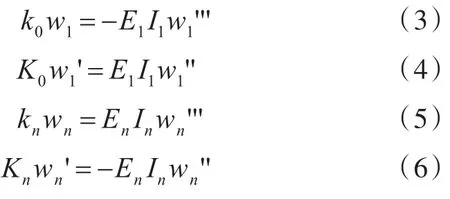
式中，wn，En，In分別為尾端邊界處梁的位移、彈性模量和剖面慣性矩。

對于中間第 i個彈簧（0＜i＜n），其對應的邊界連續條件可描述為

對于n跨連續梁結構，共可得到4+4（n-1）=4n個邊界方程。將位移函數式（1）代入到這4n個邊界條件中，并將位移函數的某4n個系數視為待求量進行求解，可得到這4n個系數與剩下的n×（M+1）個系數之間的關系式。假設每跨位移級數的-2，-1，1，2項為待求量，而剩余的為獨立變量，則該關系式可表示為

式中，Cb為Aix和Aiy形函數系數之間的關系矩陣，其中，

此時，獨立的未知系數的個數剩下n×（M+1）個，由此構造出的位移函數即可滿足該邊界條件，并表示為

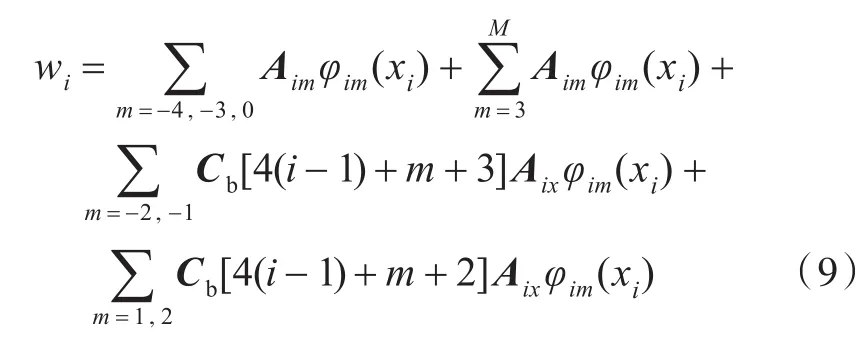
1.2.3 基于哈密頓原理推導平衡方程

根據哈密頓原理，可推導出任意邊界條件下連續梁在橫向載荷作用下的彎曲平衡方程，即

其中，

式中：UP，US分別為連續梁的應變能和邊界上的彈性勢能；W為外力功；δ為一次變分。

將式（11）～式（13）代入式（10）中，并將滿足邊界條件的位移表達式（9）代入式（10）中，運用伽遼金方法得到關于n×（M+1）個獨立系數的代數方程組，然后求解該方程組，即可得到n×（M+1）個未知系數值。將這些系數值回代到式（9）中，得到該邊界條件下的位移，根據梁結構的應力、轉角、截面彎矩、截面剪力整體與位移的微分關系，即可求得相應的物理量。

1.3 算例驗證

為驗證本文解析法的正確性，基于某三跨梁模型設計了2種邊界條件進行計算。邊界條件1模擬的是兩端固支、中間支座垂向固定的情況，如圖2所示。邊界條件2模擬的是彈性支撐下多跨梁的情況。為計算簡便，梁截面形狀和材料屬性沿長度方向均相同，各跨距li均為10 m（總長L=30 m），彈性模量E=210 GPa，泊松比 ν=0.3。梁截面為T型材，腹板高400 mm，腹板厚8 mm，面板寬150 mm，面板厚14 mm，帶板寬1 000 mm，帶板厚15 mm。假設該三跨梁受到了3組輪印載荷作用，每組輪印載荷簡化為2個集中力，分別為：F1，1=80 kN，F1，2=120 kN；F2，1=60 kN，F2，2=60 kN；F3，1=120 kN，F3，2=80 kN。每組輪印載荷集中力之間的間距 D1，D2，D3分別為 4，6，4 m。每組輪印載荷的首個集中力與連續梁最左端支座的間距X1，X2，X3分別為5.8，11.8，20.5 m。

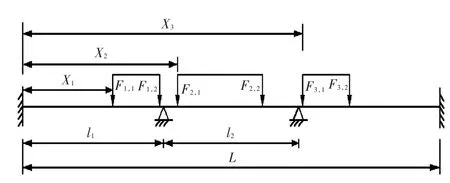
圖2 邊界條件1下的三跨梁模型示意圖Fig.2 Schematic diagram of the three-span beams model under boundary condition 1

計算邊界條件1時，將兩端的位移彈簧剛度系數取為較大值來模擬，均設為k0=kn=1×1010N/m，兩端的轉角彈簧剛度系數均設為K0=Kn=1×1010（N·m）/rad。邊界條件2模擬的是彈性支撐下的多跨梁情況，計算時將兩端的位移彈簧剛度系數均設為k0=kn=1×108N/m，轉角彈簧剛度系數均設為 K0=Kn=1×103（N·m）/rad，中間支座剛度系數分別設為 k1=5×107N/m，k2=7×107N/m。表1所示為邊界條件1下截斷數M取值對位移結果的影響。表2所示為本文方法和有限元法計算得到的各跨最大位移值的對比。圖3和圖4所示為2種邊界條件下多跨梁的整體位移、截面彎矩及截面剪力計算結果與有限元結果的對比。

由表1可以看出，當截斷數M=10時，整個計算趨于穩定，計算結果的收斂性較好。由表2可以看出，兩種方法計算結果的誤差較小。

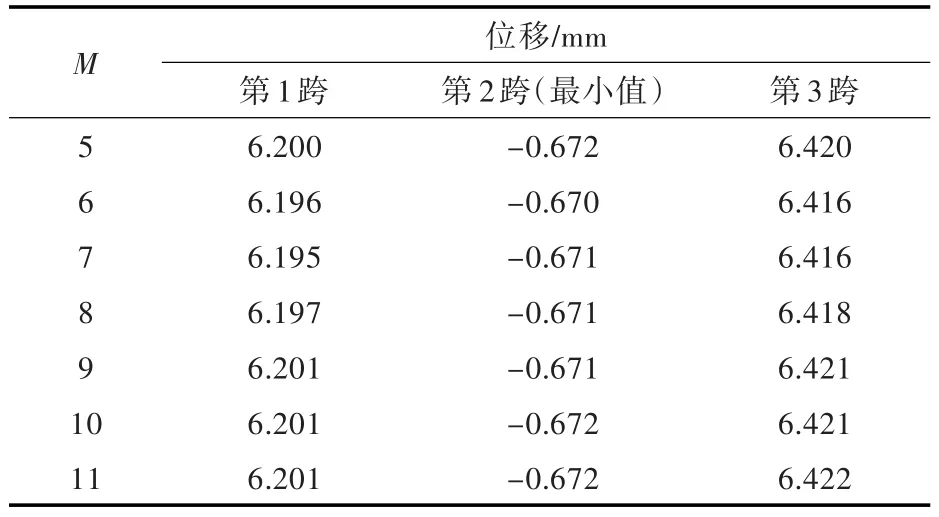
表1 邊界條件1下M取值對位移結果的影響Table 1 The impacts of M value on displacement under boundary condition 1

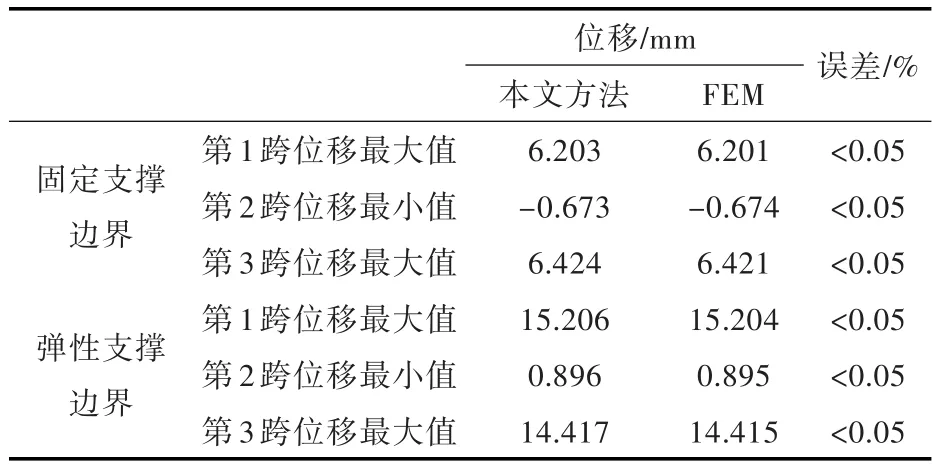
表2 各跨位移計算結果對比Table 2 The comparisons of calculated displacement for each span

圖3 邊界條件1下本文方法與有限元計算結果對比Fig.3 Result comparisons of the proposed method and FEM under boundary condition 1

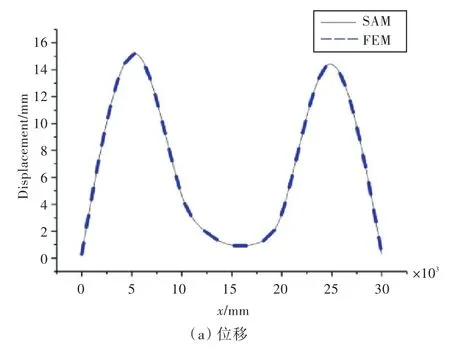
圖4 邊界條件2下本文方法與有限元計算結果對比Fig.4 Result comparisons of the proposed method and FEM under boundary condition 2

由圖3和圖4可以看出，剪力圖為一系列水平直線，而本文所選用的正弦、余弦形式的形函數對于水平直線模擬需較多的項數，綜合考慮，將截斷數取為M=40。綜合表2及圖3和圖4的計算結果，可看出本文方法計算得到的整體位移、截面彎矩及截面剪力與有限元計算的結果基本重合，驗證了本文方法的正確性。同時，本文方法相對于有限元法計算便捷，設置簡單，故有較好的工程應用價值。

2 輪印載荷下多跨梁最危險工況分析

2.1 物理模型

輪印載荷作用下多跨梁最危險工況的問題分析可描述如下［8］：給定多跨梁幾何結構、輪印載荷組的數量及輪印載荷大小，尋求輪印載荷作用下的最危險布置工況，即使某一個跨梁的截面彎矩、截面剪力或整體位移取得最大值。由于輪印載荷布置位置的搭配較多，很難直接判斷出多跨梁產生最大內力時所對應的最危險工況位置，故借助遺傳算法對該問題進行優化計算。

圖5所示為輪印載荷作用下多跨梁物理模型。假設有e組輪印載荷作用于多跨梁上，第j組輪印載荷中輪印載荷個數為 sj，Fj，a為第j組輪印載荷中第a個輪印載荷的大小，Xj為第j組輪印載荷的首載荷與多跨梁左端的間距，Dj，a為第j組載荷第a個輪印與第a+1個輪印之間的間距。

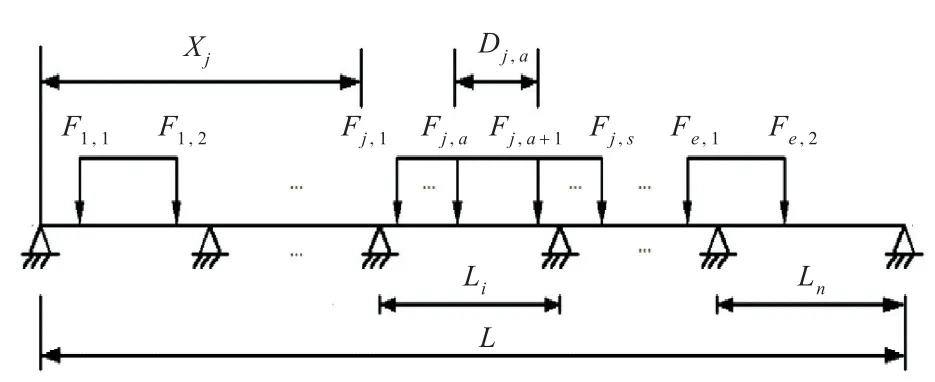
圖5 多跨梁幾何模型及其輪印載荷示意圖［8］Fig.5 Schematic diagram of the multi-span beams model under multiple patch loading［8］

2.2 數學模型

2.2.1 設計變量

在分析輪印載荷作用下多跨梁最危險工況時，變量為各輪印載荷的布置位置。對應上述物理模型，當一組輪印中的首載荷（一組輪印載荷中的第1個載荷）位置確定時，該組輪印載荷的布置位置也就相應得到確定，故以每組輪印的首載荷與多跨梁左端的間距Xj作為該問題的設計變量。

2.2.2 目標函數

在分析輪印載荷作用下多跨梁最危險工況的目標函數為多跨梁上某跨的最大彎矩Mi或最大剪力FSi或最大變形wmax時，每個載荷布置工況下的目標函數值通過本文推導的半解析法進行求解，結果表明具有較好的精度，且相對于有限元法極大地減少了計算時間。

2.2.3 約束條件

在實際船舶的裝載甲板上，相鄰車輛之間的間距需要滿足一定的要求，因此在輪印載荷作用下多跨梁最危險工況分析的約束條件為相鄰2組輪印載荷的間距大小。約束條件如式（14）所示，式中Con1j，Con2j分別為第j組與第j+1組輪印載荷之間需要滿足的最小間距及最大間距。

2.3 計算實例

運用本文多跨梁彎曲計算方法并結合遺傳算法對上述優化問題進行求解。為方便對比，本文選取文獻［8］中的方案2進行計算。該方案的幾何參數與截面參數及每組載荷的數量、大小和間距均與2.1節算例驗證所用的三跨梁相同，而每組載荷的首載荷與多跨梁左端的間距X1，X2，X3是需要求解的設計變量，其取值范圍分別為0.5～6 m，10～14 m和20～25.5 m。約束條件為相鄰2組輪印載荷之間的最小間距不小于1 m，最大間距不大于5 m。邊界選用兩端剛性固定、中間支座垂向固定的約束條件，即首、尾兩端的位移彈簧剛度系數均設為1×1010N/m，兩端的轉角彈簧剛度系數均設為1×1010（N·m）/rad，而中間的位移彈簧剛度系數設為1×1010N/m。使用Matlab軟件自帶的遺傳算法ga函數尋求最危險工況的結果，該函數可以處理設計變量連續取值的優化問題。計算時，種群個數設為100個，遺傳代數設為100代。最終優化結果與文獻［8］計算結果的對比如表3所示。

由表3可以看出，相比文獻［8］，由于本文采用的遺傳算法可以處理設計變量連續取值的優化問題，所以能夠找到更精確的最危險輪印載荷布置工況。該工況的最大彎矩或最大剪力比文獻［8］的工況更大，同時，設計變量連續取值也更貼近工程實際，這是因為車輛在裝載甲板上的移動是連續的，而不是階躍的。

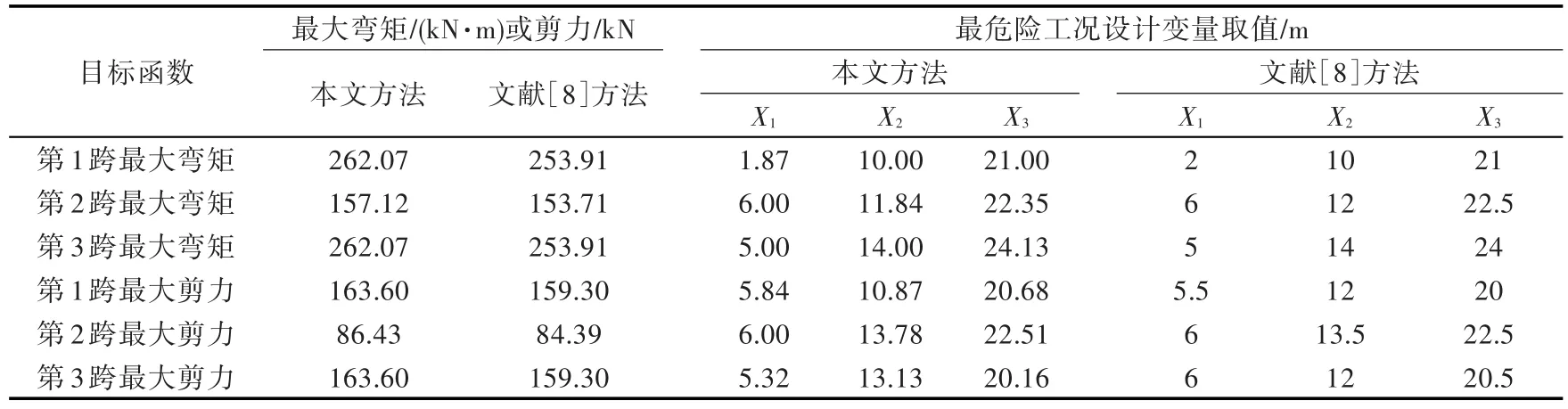
表3 多跨梁最危險工況計算結果Table 3 Numerical results of the worst-case analysis of multi-span beams

3 結 論

本文基于能量原理并結合邊界條件，分析了任意邊界條件下連續多跨梁結構的彎曲問題。通過將本文方法計算的結果與有限元法計算結果進行對比，驗證了本文方法的正確性。運用此方法分析輪印載荷下多跨梁的最危險工況，得到了滿意的結果，其計算精度較高，耗時少。根據本文的研究，主要得到如下結論：

1）推導的計算方法隨著傅里葉級數截斷數的增加，計算結果很快收斂，數值穩定性較好；與算例的有限元法計算結果相比，計算的位移誤差小于0.05%。同時，由于基于能量原理，本文計算過程不需要平衡方程，故易于推廣到板結構及其他更復雜的結構。

2）在計算分析輪印載荷下多跨梁最危險工況時，運用此方法得到了更精確的最危險布置工況。