基于壓縮感知的CT重建算法的研究進展

尹娟，范醫魯，秦紹華

1. 山東省千佛山醫院 醫學工程部，山東 濟南 250014；2. 山東師范大學 物理與電子科學學院，山東 濟南 250358

引言

自從1927 年，英國工程師Hounsfield 研制成功第一臺醫用CT 裝置以來，CT 在臨床領域一直發揮著重要作用。Hounsfield 和Cormack 兩位沒有醫學經歷的科學家，也因為其在CT 領域的開創性工作，在1979 年被授予諾貝爾生理或醫學獎。CT 技術主要是利用X 射線穿透物體的衰減信息來進行物體斷層圖像信息的重建[1]。從投影重建圖像本質上屬于數學反問題，重建算法是CT 技術的核心理論問題。

1 傳統的CT重建算法

CT 是通過具有一定能量和穿透能力的X 射線與物體相互作用的原理而成像的。如當一定能量的X 射線穿過物體時，X 射線的強度會發生衰減，其衰減程度與物體的成分、

厚度有關，如果物體是均勻的，X 射線的強度按指數規律衰減，遵循Lambert-Beer 定律：

其中I0位射線原始強度，I 為射線穿透物體后的強度，μ 為被測物體的衰減系數，l 為射線穿過物體的長度。

如果物體是非均勻的，如圖1 所示，假設其衰減系數分布為μ(x,y)，則其衰減程度為沿投射路徑L 的線積分

投影數據b

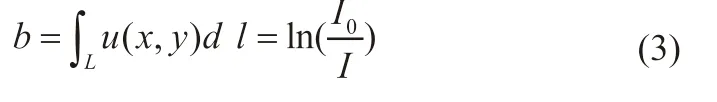
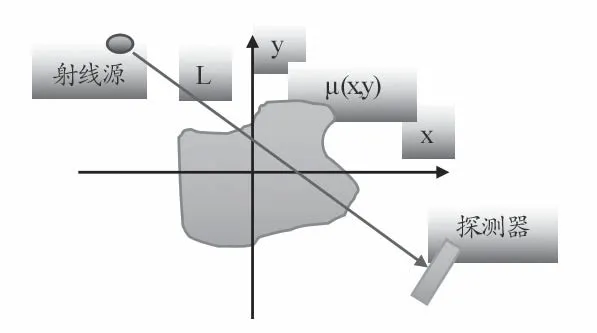
圖1 X射線穿過非均勻物體示意圖

CT 重建就是根據投影數據b，求解μ(x, y)的過程。CT重建算法主要分為解析類（Analytic Reconstruction，AR）和迭代類（Iterative Reconstruction，IR）。解析類重建算法以Randon 變換為理論基礎，經過長期的發展，目前已經形成了完整的理論體系。解析類重建算法主要包括二維圖像重建的濾波反投影算法（Filtering Back-Projection，FBP）和三維圖像重建的FDK 算法。FBP 算法一直都被作為CT重建算法的基礎和“金標準”。解析類重建算法發展時間較長，具有分辨率高、重建速度快等優點，但是抗噪聲性能較差，對數據的完備性要求較高。

迭代類重建算法將測量得到投影數據作為已知量，將重建圖像作為未知量，建立方程組，通過解方程來重建未知圖像。設圖像X 有M 個像素，投影數據B 有N 個測量值，則圖像X 和投影數據B 之間的關系用方程組可以描述為

2 基于壓縮感知的CT重建算法

近年來，為了減少X 射線對于病患的危害，對減少CT 掃描的時間和降低掃描的強度提出了新的要求[4-5]；同時隨著CT 應用場景的擴展，有些應用也需要快速成像或者減少CT 掃描的角度。這都導致CT 投影數據的不完整，如何在投影數據不完整的條件，保證CT 重建圖像的質量，是CT 重建算法面臨的新挑戰。

2.1 壓縮感知理論

壓縮感知理論（Compressed Sensing，CS）是一項不同于傳統數據處理技術的全新理論，其發展以2006 年Donoho[6]在理論上取得的重大突破為標志，目前壓縮感知理論正在快

如果觀測陣滿足RIP（Restricted Isometry Property）特性，那么可以從壓縮后的觀測數據準確地恢復出信號。如果觀測陣是高斯隨機矩陣或貝努力矩陣，那么M 的下限是

其中C 為一正常數。正常情況下，由于M＜N，從y 恢復x 是不可能的，但當滿足x 的稀疏性和觀測陣的RIP 特性要求時，可以利用非線性優化的方法完美的恢復出信號，即：

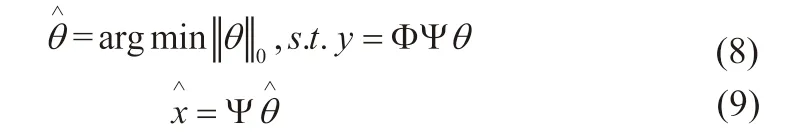
常用的恢復算法有凸優化算法和貪婪算法兩類，凸優化算法的代表是BP（Basis Pursuit）算法[7]，貪婪算法包括MP（Matching Pursuit）算法[8]、OMP（Orthogonal Matching Pursuit）算法[9]和CoSaMP（Compressive Sampling Matching Pursuit）算法[10]等多種算法。

2.2 基于壓縮感知的重建算法

在投影數據不完整的條件下，傳統的重建算法在重建速度和重建精度方面都無法滿足實際應用的需求。壓縮感知理論為不完整投影數據重建問題提供了新的思路。一方面，壓縮感知理論對信息的采集位置沒有要求，另一方面，壓縮感知理論對于信息的采集數量要求較低，這使得根據不完整數據進行CT 圖像重建成為可能。綜合公式(4)、(8)、(9)，可得到基于壓縮感知的 CT 不完整投影數據重建過程如下

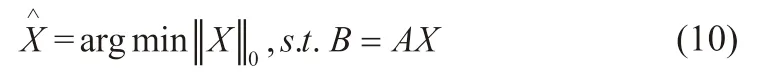
這個問題可以通過轉化為優化問題求解

g(x)為正則化項，在投影數據不完整條件下，通過數據保真度重建圖像，在數學上屬于一個不完備方程求解，需要添加先驗知識來作為正則項，對優化過程進行約束。正則化可以分為基于圖像稀疏化的方法，以及利用先驗圖像約束的方法兩大類[11-14]。常用的稀疏化有L0 范數，L1 范數，TV（Total Variation）以及字典學習等不同方法，先驗圖像包括人體解剖結構，患者早期的醫學影像信息以及其他模態信息。優化問題的求解可以通過近端算法（Proximal Algorithms）實現[15-17]。

2.2.1 基于圖像稀疏化的 CT不完整投影數據重建

圖像稀疏化可以分為基于范數和基于字典等不同方法。L0 范數和L1 范數是傳統的正則化方法，廣泛應用于各種信號稀疏化場景。近年來，隨著對圖像特點的分析，基于圖像梯度L1 范數的TV 方法，在圖像稀疏化過程中獲得了廣泛應用。2008 年Sidky 等[18]利用TV 最速下降法和凸集投影約束相結合的方法進行了CBCT 圖像重建。近幾年，許多研究者基于TV 方法，對CT 圖像重建算法進行了改進[19-21]。2015 年Hongliang 等[22]將基于L1 范數的TV 形式與基于L0范數的TV 形式相結合，代替傳統的基于L1 范數的TV 形式，有效改善了CT 重建效果。但是TV 方法用圖像的梯度特征來稀疏圖像，無法區分圖像的結構信息和噪聲，容易出現光滑過度的現象，造成CT 圖像器官輪廓和紋理的模糊。

字典學習是一種有效的圖像稀疏方法，其通過對圖像進行訓練的方法，得到適合圖像稀疏表示的字典[23]。近幾年，許多研究者嘗試利用字典學習的方法稀疏化CT 圖像，進行重建。2012 年，Xu 等[24]用字典學習的方法，對低劑量CT圖像進行了重建。2014 年提出的ASDL 算法[25]，在字典學習的過程中，綜合考慮圖像的方向和尺度信息，來消除CT 圖像中的偽影，改善重建效果。2015 年，Shi 等[26]根據CT 三維圖像的特點，綜合考慮圖像的空間和時間相關性，建立三維字典學習方法，有效提高了CT 圖像的重建效果。由于字典學習的方法在字典訓練過程中，將圖像先分塊學習，再合并處理。因此容易產生塊狀噪聲。字典學習方法在分塊過程中，并沒有考慮圖像塊之間的空間相關性，因此其稀疏化效果和對圖像結構信息的保護程度還有待提高。

2.2.2 基于先驗圖像的CT不完整投影數據重建

CT 不完整投影數據重建問題，從數學本質上屬于欠定方程的求解問題，先驗知識的增加有利于方程的求解。人體解剖結構，以及患者其他醫學影像信息，都可以作為先驗知識，改善CT 重建效果。加入先驗知識的CT 重建過程可以表示為

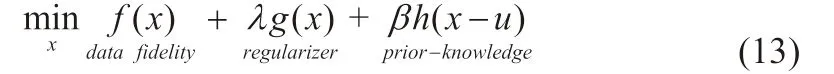
其中u 為先驗圖像，h(x-u)表示先驗圖像與重建圖像的差值，為權重系數。先驗知識可以為重建過程提供更多的信息，有利于重建進行，但是先驗圖像與真實圖像是不同的，如果重建過程過分依賴先驗圖像，則會掩蓋重建圖像的細節信息，如果先驗圖像的權重過低，則對于重建圖像的改善效果有限，因此在重建過程中，如何平衡先驗圖像的權重是一個關鍵問題。

2008 年，PICCS 算法利用壓縮感知理論，對基于先驗圖像的CBCT 不完整投影數據重建問題進行了研究[27]。此后，許多研究者在此基礎上，進行了進一步探討。2015 年提出的pPICCS 算法[28]，針對配準對CT 圖像重建效果的影響進行了研究，對PICCS 算法進行了改進。2015 年，Lubner 等[29]對PICCS 算法在腹部CT 圖像上的重建效果進行了分析，從臨床應用的角度，對減少CT 照射劑量和保證圖像質量的平衡問題進行了研究。2017 年約翰霍普金斯大學的Stayman 也對應用CT 圖像作為先驗知識，對CBCT圖像的質量提升問題進行了研究，并對先驗知識的權重問題進行了分析[30-32]。先驗知識的加入，有助于CT 不完整投影數據的重建。但是患者先期獲得的圖像與當前的CT 圖像存在一定的差異，這對基于先驗圖像的CT 不完整投影數據重建的精度，造成了一定的影響，如何有效地利用先驗知識是基于先驗知識的CT 不完整投影數據重建的關鍵。

3 總結

基于壓縮感知理論，在CT 重建過程中應用迭代算法，可以有效地減少CT 掃描的劑量和角度，具有很好的發展前景。近年來，隨著人工智能的發展，應用深度學習網絡來解決CT 重建問題，也引起了業內學者和廠商的重視[33]。基于深度學習網絡的啟發，卷積稀疏編碼近年來開始用于圖像稀疏化，基于卷積稀疏編碼的CT 重建算法也開始用于CT 重建[34]。深度學習網絡和卷積稀疏編碼在CT 重建算法中的應用，有效地提高了CT 圖像的質量，但是深度學習網絡的參數，以及卷積稀疏編碼的字典都需要從大量的數據中學習得到，需要強大的運算能力和時間保證，以及病人大數據信息的保證，這些都增加了其在實踐中應用的難度。基于深度學習網絡和卷積稀疏編碼的CT 重建算法同樣面臨投影數據不完整的問題，如何將壓縮感知理論，與深度學習網絡和卷積稀疏編碼等技術相結合，有效地提高CT 重建質量，是基于壓縮感知的CT 重建算法面臨的重要問題。