鋼混組合橋墩在車輛撞擊下的動力性能研究?

巫業雙 張南 胡勝良 李界全 高閔

(1.中機國際工程設計研究院有限責任公司(華東分院) 南京211800)

(2.南京工業大學土木工程學院 211800)

引言

由于道路建設和城市立交數量的增長,車橋碰撞事故頻繁發生,造成較大的經濟損失。提高橋墩的抗撞性能,對橋墩進行防撞設計,逐漸成為工程界和學術界研究的熱點[1-4]。近年來,我國出現了為數不多的鋼骨混凝土組合橋墩[5],而目前對鋼骨混凝土組合橋墩的研究還相對較少。

在橋墩抗撞方面,文獻[3]通過落錘試驗和有限元模擬給出了一個橋墩撞擊峰值的估算公式; 文獻[6]通過有限元研究了鋼筋混凝土柱在車輛撞擊下的動態響應; 在鋼骨混凝土柱式結構的抗壓性能方面,文獻[7]、文獻[8]分別對鋼骨混凝土柱進行了軸壓和偏壓試驗; 文獻[9]采用有限元進行了細長鋼骨混凝土柱在軸壓下的力學性能研究。在鋼骨混凝土柱式結構的抗震性能方面,對非對稱配筋鋼骨混凝土柱[10]、內埋空間鋼構架鋼骨混凝土柱[11]和鋼骨超高強混凝土框架柱[12]進行了抗震性能的試驗研究。文獻[13]對低周反復荷載作用下型鋼再生混凝土短柱的破壞形態、破壞機理及抗剪強度進行了分析。在鋼骨混凝土柱式結構的抗剪計算方面,日本公路橋梁抗震規范綜合考慮了橋墩尺寸、配筋率、以及箍筋與橋墩軸向夾角對墩柱抗剪能力的影響,給出了橋墩抗剪能力計算公式[14]。美國ATC-32 簡單地處理了延性發展對混凝土抗剪能力的影響,提出了名義抗剪強度由混凝土和鋼材兩部分疊加的計算方法[15]。文獻[16]對高強、超高強混凝土結構進行了試驗分析,得到普通型鋼混凝土柱和型鋼高強混凝土柱的受剪承載力計算公式; 文獻[17]采用桁架-拱模型提出了鋼骨混凝土橋墩抗剪承載力計算公式。然而,有關鋼骨混凝土柱式構件撞擊抗剪性能的研究還較為少見。

在普通鋼筋混凝土結構中內置鋼骨架,提高普通混凝土橋墩的抗撞性能,抵御車輛撞擊荷載,對保障行車安全和交通通暢具有重要的工程和社會意義。為深入研究內置鋼骨架后混凝土橋墩的抗撞性能,本文通過4 根橋墩模型的車輛撞擊試驗對比分析了內置不同鋼骨形式的混凝土橋墩抗撞性能。建立了內置鋼骨的混凝土橋墩撞擊抗剪承載力計算公式,將對應側向靜力試驗結果代入公式確定了有關參數的取值,并將撞擊抗剪承載力計算值與試驗值進行了對比。

1 車輛撞擊試驗概述

1.1 試件設計

設計了4 根橋墩模型進行車輛撞擊試驗,試驗模型截面形式如圖1 所示。為比較內置不同鋼骨形式橋墩的抗撞性能,試驗橋墩采用了近似的橫向配鋼率和相同的縱向配鋼率。圖1中SRCP-1 為用于試驗對比的普通混凝土橋墩模型、SRCP -2 為內置角鋼橋墩模型、SRCP -3為內置槽鋼橋墩模型,SRCP-4 為內置雙圓鋼管橋墩模型。試件設計參數見表1。鋼材力學性能見表2。

圖1 試件尺寸與截面配筋(單位： mm)Fig.1 Specimen dimensions and steel details(unit: mm)

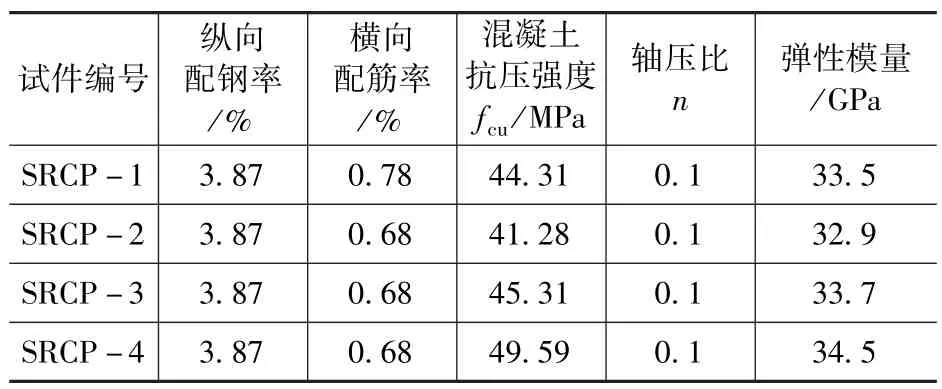
表1 試件設計參數Tab.1 Design parameters of specimens

表2 鋼筋與鋼材材料性能Tab.2 Material properties of reinforcement and steel

1.2 試驗加載方案

忽略樁土效應的影響,本試驗采用底端固支,頂端鉸接,撞擊試驗加載裝置如圖2 所示。通過地錨桿固定橋墩模型,承臺側面與反力墻接觸,在墩頂通過拉壓傳感器按0.1 的軸壓比施加軸向壓力,該軸向壓力和墩頂側向約束共同作用,用于模擬橋墩上部荷載。通過改變下落重物的高度來控制撞擊能量,撞擊位置參考大型卡車撞擊橋墩的作用范圍以及出現剪切破壞的剪跨比,取距承臺500mm。為直接研究橋墩的抗撞性能,采用剛性撞擊頭,撞擊頭后部安裝沖擊力傳感器。通過動態數據采集系統采集各測點應變、橋墩撞擊點位移以及小車的撞擊速度。

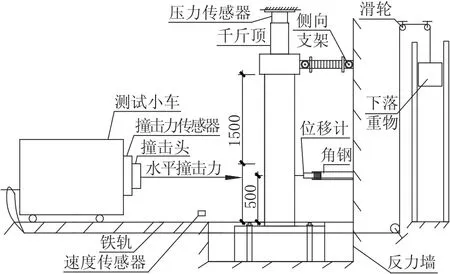
圖2 撞擊試驗裝置示意(單位： mm)Fig.2 Schematic diagram of test loading(unit: mm)

2 試驗結果與分析

2.1 撞擊開裂和破壞狀態分析

通過重物下落拉動小車水平撞擊試驗橋墩,控制下落重物的下落高度使得小車撞擊橋墩時具有相近的撞擊速度,橋墩模型最終的撞擊破壞模式如圖3 所示。

圖3 橋墩破壞形態Fig.3 Impact failure modes of bridge piers

由圖3 可知: 試驗模型均為剪切破壞,普通鋼筋混凝土橋墩在出現斜裂縫后很快形成主斜裂縫,破壞較快,內置鋼骨架后墩身的破壞較為緩慢且局部破壞更完整。內置鋼骨架的銷栓作用有效抑制了墩身的剪切滑移。

橋墩模型撞擊開裂和撞擊破壞峰值力見表3。由表3 可知,內置鋼骨架后,橋墩模型開裂狀態和破壞狀態的峰值力明顯提高。與試件SRCP-1相比,試件SRCP-2 的撞擊開裂峰值力和撞擊破壞峰值力分別提高24.22% 和11.79%,試件SRCP-3 的撞擊開裂峰值力和撞擊破壞峰值力分別提高65.90%和35.46%,試件SRCP-4 的撞擊開裂峰值力和撞擊破壞峰值力分別提高81.02%和44.67%。縱向配鋼率相同時,試件SRCP -4的抗撞性能較好。

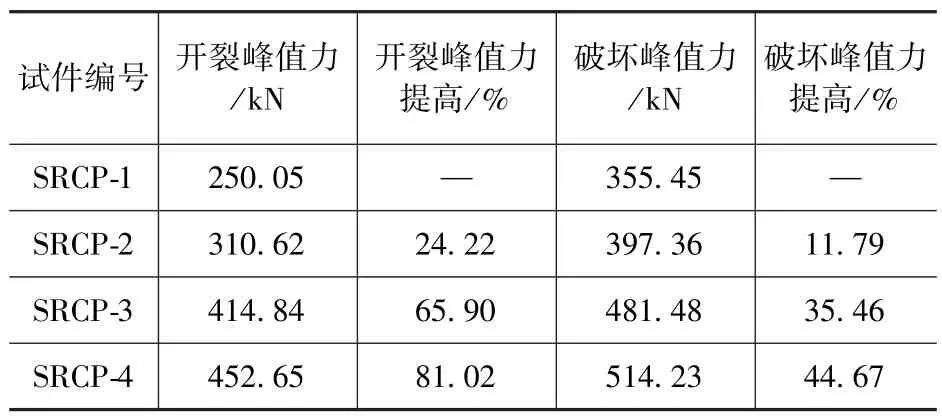
表3 橋墩模型撞擊力對比Tab.3 Comparison of impact force of bridge pier models

圖4 為橋墩模型開裂和破壞狀態撞擊力時程曲線。

圖4 橋墩模型撞擊力時程曲線Fig.4 Time-history curves of impact force of piers

小車撞擊后墩身未開裂時,主要由混凝土抵御車輛撞擊,此時撞擊力下降段較緩,撞擊力作用時間基本在20ms 左右,撞擊力波形接近半波正弦波形,如圖4a 所示。小車撞擊后墩身開裂時,鋼材的抵御作用變大,撞擊力到達峰值后迅速下降,撞擊力作用時間延長至25ms 左右,撞擊力波形更接近三角形波形,如圖4b 所示。該結果為墩柱撞擊作用效應的分析提供了一定的參考價值。

2.2 墩身撞擊位移分析

試驗小車撞擊下橋墩模型開裂狀態的位移時程曲線如圖5 所示。

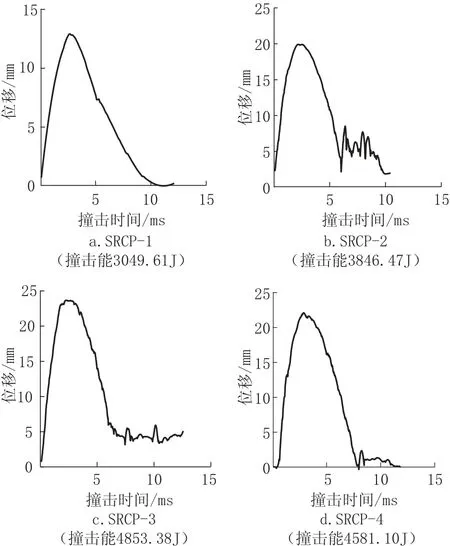
圖5 橋墩模型撞擊開裂位移時程曲線Fig.5 Displacement time-history curves of pier models in crack

由圖5 可知,撞擊位移峰值與墩身側向剛度及撞擊能量有關。試件SRCP-4 具有較好的抗撞擊開裂能力。

（2）誘殺蚜蟲：用20×40cm黃板，畝插置、懸掛50—100面，高出植株頂部，7－10天重涂一次機油，誘殺蚜蟲。

2.3 墩身撞擊應變時程分析

為進一步研究車輛撞擊荷載作用下內置鋼骨混凝土橋墩的動態反應,在試驗模型剪切區混凝土、鋼筋及型鋼表面粘貼應變片。選取典型的橋墩模型進行分析。橋墩模型應變片布置如圖6 所示,將撞擊點背面的橋墩底部記為原點O(0,0),混凝土應變片沿撞擊點與原點連線粘貼。

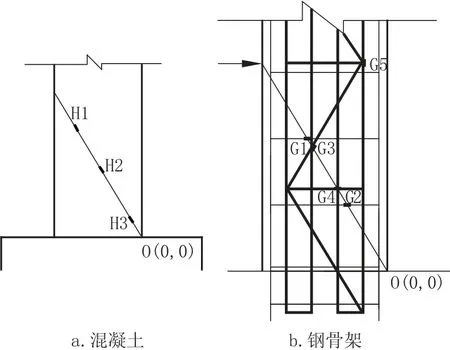
圖6 應變片布置Fig.6 Layout of strain gauges

1.剪切區混凝土應變時程分析

撞擊試驗測得開裂階段典型的墩身剪切區混凝土應變時程曲線如圖7 所示。圖7a 和圖7b 分別為試件SRCP-1、SRCP-4 的混凝土應變時程曲線。

圖7 混凝土應變時程曲線Fig.7 Time-history curves of concrete strain

由圖7 可見,撞擊作用下,內置鋼骨架后,H1、H3 測點處混凝土應變略有減小,墩身中部H2 測點處混凝土應變減小明顯。內置的鋼骨架在橋墩模型主斜裂縫形成時改變了整個橋墩的應力分布,從而提高了橋墩模型的抗撞擊能。

2.剪切區鋼筋應變時程分析

圖8 為試驗小車撞擊下(撞擊能4581.10J)測得的開裂階段典型的鋼筋應變時程曲線。圖9 為SRCP-2 ～SRCP-4 在開裂狀態下G4 測點處的鋼筋應變時程曲線。

圖8 SRCP-4 鋼筋應變時程曲線Fig.8 Time-history curves of steel strain of SRCP-4

圖9 鋼筋應變時程曲線對比Fig.9 Comparison of time-history curves of steel strain

由圖8 可見,相同撞擊能量下,不同位置的鋼筋應變相差較大。在撞擊能為4581.10J 的條件下,G5 測點處鋼筋應變較小(300.857με),表明墩身彎曲變形較小; G2 測點處鋼筋屈服,G1測點處鋼筋應變651.08με,表明墩身中下部區域的斜拉應力較大; G3 測點處鋼筋應變(515.255με)與G1 測點處鋼筋應變(651.08με)已相對接近,表明內置的斜筋分擔了部分的斜拉應力。

由圖9 可見,內置雙圓鋼管的橋墩模型(SRCP-4)斜筋應變峰值最小,這表明內置不同的鋼骨形式對墩身應力分布產生了不同影響,內置雙圓鋼管橋墩墩身內受拉鋼筋應變較小,具有進一步承擔荷載的能力。

3 橋墩撞擊抗剪承載力分析計算

3.1 材料的動態力學性能

依據文獻[18],定義K1為混凝土動強度提高系數,K2為鋼材動強度提高系數。混凝土動抗壓強度計算按式(1)。假定鋼材屈服后仍保持屈服強度,鋼材的動抗拉強度計算按式(2)。

混凝土的動彈性模量采用式(3)計算[19],鋼材的動彈性模量取其靜彈性模量[20]。

式中:為混凝土動彈性模量;Ec為混凝土靜彈性模量。

將試驗測得的材料應變率(與撞擊能有關),代入式(1)、(2)、(3)得材料的動態力學參數,結果見表4。

表4 鋼材和混凝土的動態力學參數Tab.4 Dynamicmechanics parameters of steel and concrete

3.2 橋墩模型撞擊抗剪強度試驗峰值

將試驗橋墩模型按約束條件簡化,如圖10所示。由于撞擊作用時間很短,將撞擊力到達峰值時橋墩模型的狀態近似視為彈性狀態,得到橋墩撞擊抗剪強度試驗峰值公式為:

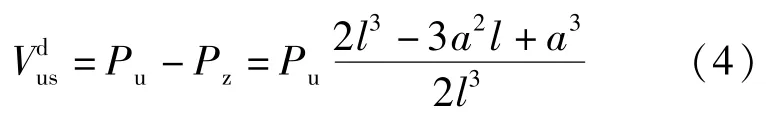
式中:為橋墩撞擊抗剪強度試驗峰值;Pu為撞擊力峰值;Pz為墩頂支反力;a為加載點高度(500mm);l為橋墩計算高度(1500mm)。

3.3 撞擊抗剪強度計算

1.撞擊抗剪強度計算模型

采用疊加原理計算結構抗剪強度是目前較為常見的方法。本文在現有抗剪強度計算公式的基礎上進行修正,給出內置鋼骨的混凝土橋墩撞擊抗剪強度計算公式: (1)用材料的動態力學性能取代靜態力學性能; (2)考慮由裂縫發展方向的隨機性引起的箍筋及鋼斜撐的應變不均勻; (3)考慮型鋼的強度折減。橋墩動態抗剪強度計算模型如圖11 所示,圖中,為混凝土動抗剪強度;為型鋼動抗剪強度;為鋼斜撐動抗剪強度;為箍筋動抗剪強度;N為軸壓力。

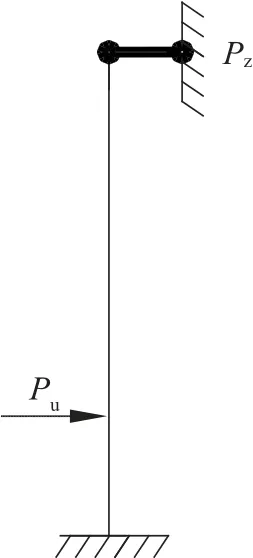
圖10 橋墩計算簡圖Fig.10 Calculation diagram of pier

圖11 橋墩動態抗剪強度計算模型Fig.11 Calculationmodel of impact strength of bridge pier

橋墩模型撞擊抗剪強度計算公式如下:

式中:λ為剪跨比;b為模型截面寬度;h0為模型截面有效高度;Asw為型鋼截面面積;為鋼材動彈性模量與混凝土動彈性模量的比值;為箍筋動態抗拉強度;Asv為箍筋截面面積;s1為箍筋間距;為斜筋動態抗拉強度;Aw2為斜筋截面面積;φ為斜筋與豎直方向的夾角;s2為斜筋等效間距;為型鋼動態抗拉強度;tw1為型鋼腹板等效厚度;hw1型鋼腹板等效高度;n為軸壓比;Aw為鋼材截面面積;h為橋墩截面高度;n1為箍筋應變不均勻系數,n2為斜筋應變不均勻系數,n3為型鋼強度折減系數。

為得到n1、n2、n3的具體取值,進行了與撞擊試驗對應的4 根橋墩模型側向靜力試驗。側向加載點與撞擊位置相同。側向靜力試驗結果如表5 所示。圖12 為橋墩模型的側向靜力加載破壞形態。

表5 側向靜力試驗結果Tab.5 Results of static test

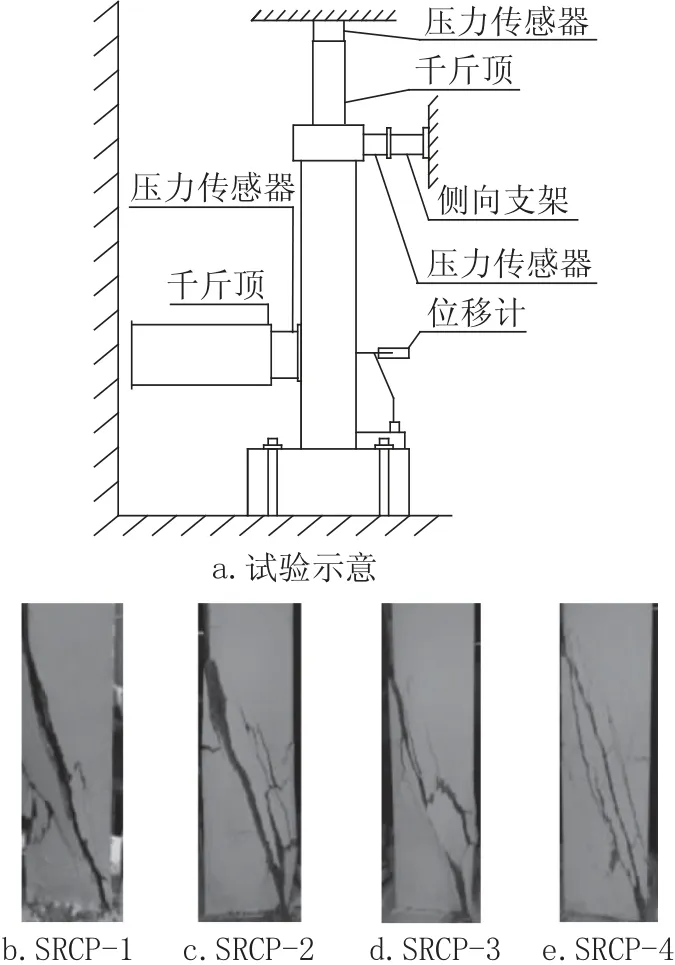
圖12 橋墩靜力破壞形態Fig.12 Static failure modes of bridge piers

將材料的靜態力學性能和側向靜力試驗結果帶入式(3) ～式(5)解得n1、n2、n3的值分別為0.591、0.521、0.520。

2.計算值與試驗值對比分析

由于峰值撞擊力作用時間較短,目前,通常選取等效撞擊力對結構進行設計[4,21-22]。根據文獻[23]的研究結果,由于撞擊試驗橋墩內置鋼骨的形式不同,撞擊力等效系數存在差異,結合本文的車輛撞擊試驗,從偏安全的角度,建議撞擊力等效系數的取值為0.85,即:

橋墩撞擊抗剪強度計算值與橋墩等效撞擊抗剪強度試驗值的對比結果見表6。

表6 橋墩撞擊抗剪強度計算結果與等效撞擊抗剪強度試驗值對比Tab.6 Comparison between calculation results and equivalent test results for dynamic shear strength of piers

由表6 可知,本文建議的公式能較好地預測橋墩的撞擊抗剪承載力,具有一定的設計參考價值。

4 結論

1.剪切區混凝土受壓為主,內置鋼骨架后橋墩模型的開裂撞擊力峰值、破壞撞擊力峰值均有明顯提高,內置不同鋼骨形式的橋墩抗撞性能存在較大差異,內置雙圓鋼管的混凝土橋墩是一種抗撞性能較好的橋墩。

2.內置的鋼骨架改變了墩身的應力分布,有利于箍筋進一步承擔更大的拉力。同時,內置的鋼骨架改變了墩身側向剛度,提高了橋墩的抗側向變形能力。

3.采用疊加原理給出了內置鋼骨的混凝土橋墩撞擊抗剪強度計算公式,由于撞擊試驗復雜且難度較大,橋墩試驗模型數量還較少,本文計算公式具有一定的條件適用性,還需深入做大量的試驗和理論分析得到更廣泛的具有工程實用價值的計算公式。