填充墻-鋼框架結構地震易損性分析

鄭文豪

(北京市政工程設計研究總院有限公司 100082)

引言

目前對于鋼框架結構的研究主要集中在框架主體結構方面,并取得了較大進展,而對于填充墻等非結構構件及其影響并沒有充分的考慮。在傳統的結構設計中,僅考慮填充墻帶來的荷載作用,不考慮填充墻對剛度的影響,或者是僅通過周期折減系數來增大地震作用。而實際工程中,填充墻與主體結構共同承受地震作用,其對結構側向剛度、承載力、傳力機制及破壞模式等均有影響。基于此,本文采用等效斜撐方式模擬了含填充墻鋼框架結構與無墻鋼框架結構,并對兩結構進行了地震易損性分析及風險性分析,旨在為實際工程中鋼框架結構抗震設計提供一定參考。

1 填充墻模擬

1.1 等效桿模型

Saneinejad 和Hobbs[1]提出的斜撐寬度計算公式如式(1)所示。該公式也是FEMA273[2]建議采用的斜撐寬度計算公式。

式中:W為斜撐寬度;H為框架層高;L為框架梁長;λ為相對剛度系數。

填充墻框架結構中,填充墻與框架主體是相互作用、相互影響的,等效斜撐寬度計算中考慮填充墻與框架的相對剛度系數λ是符合實際情況的。Mainstone[3]在大量已有試驗數據的基礎上推導出填充墻與框架相對剛度系數λ 的計算公式,如式(2):

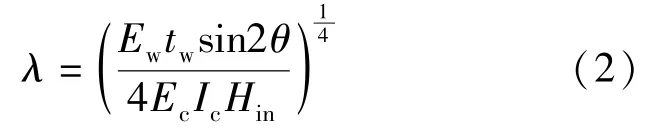
式中:tw為填充墻厚度;Hin為填充墻的高度;Ec為框架材料的彈性模量;Ew為填充墻材料的彈性模量;Ic為柱正交荷載方向的慣性矩;θ為斜撐與水平梁的夾角。

由于地震作用是往復作用的動荷載,震害中填充墻多表現為交叉斜裂縫。所以用單方向的壓桿不能正確反映地震作用下墻框的相互作用,本文在建立地震作用下墻框協同作用計算分析模型時將單對角斜撐轉化成雙對角斜撐,雙對角斜撐中每根壓桿的寬度w1均為式(1)計算斜撐寬度w的一半,如圖1 所示。其中填充墻由砌塊和砂漿砌筑而成。

圖1 等效斜撐Fig.1 Equivalent brace

1.2 填充墻本構

本文的等效斜撐材料采用文獻[4]所推薦的應力-應變關系,如圖2 所示。

圖2 砌體本構模型Fig.2 Constitutive model of masonry

圖2 中fm為砌體軸心抗壓強度平均值,fm=為砌體的抗壓強度等級;f2為砂漿的抗壓強度等級,f2≥1時k2=1。砌體抗壓強度設計值f=0.45fm,砌體抗壓強度設計值f及對應的應變εe=f/E作為砌體應力應變曲線的比例極限點,其中砌體彈性模量E根據《砌體結構設計規范》(GB50003 -2011)[5]中表3.2.5 -1計算。峰值應力下的峰值應變ε0為0.003; 殘余強度下的極限應變為2ε0,極限壓應變取3ε0。

1.3 等效壓桿模型驗證

為驗證等效壓桿可較準確地模擬實際工程中填充墻的非線性行為,對關國雄、夏敬謙[6]模型擬動力試驗進行有限元建模對比分析。關國雄、夏敬謙試驗中模型的具體尺寸見圖3a,梁柱截面尺寸見圖3b、3c。混凝土抗壓強度為9.69MPa,鋼筋屈服強度為237.5MPa,粘土磚的抗壓強度為13.72 MPa,砂漿抗壓強度為2.21MPa。梁柱截面配筋為4?8,箍筋為?4@30。

圖3 試驗及有限元模型(單位： mm)Fig.3 Tests and finite element model(unit: mm)

將相關參數代入式(1)、式(2)得到等效斜撐的相關參數如下:

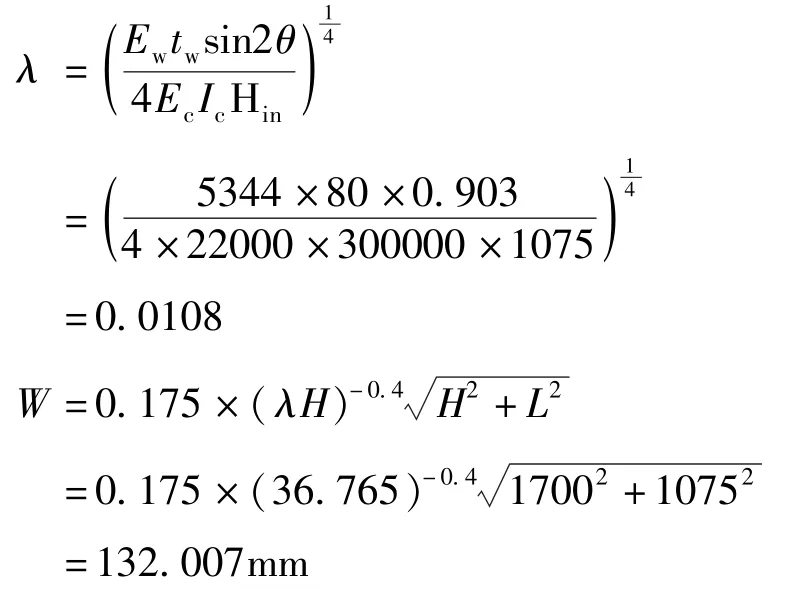
表1 等效斜撐相關參數及本構參數Tab.1 Equivalent brace parameters and constitutive parameters

利用上述等效斜撐相關參數模擬填充墻,通過梁端布置M3 鉸,柱端布置P - M2 - M3 鉸,等效斜撐中部布置P 鉸來檢測結構的非線性行為。建立ETABS 模型進行非線性靜力pushover分析,與關國雄、夏敬謙試驗結果進行對比如圖4 所示。

由圖4 可見,對于關國雄、夏敬謙的縮尺試驗,本文采用等效斜撐模擬結果與實際試驗下的內力-位移變化比較接近,故利用等效斜撐模擬填充墻是比較接近實際工況的。

圖4 基底剪力-位移曲線Fig.4 Base shear-displacement curve

2 基于IDA分析的地震易損性分析方法

2.1 地震易損性分析方法

易損性曲線是對結構處于不同破壞狀態可能發生概率的定量展示,通常以IM(地震動強度參數)為自變量軸,超越概率為因變量。由該曲線可獲得結構在給定IM下,結構地震需求反應參數(用μD表示)達到指定破壞狀態下的結構抗震能力參數(用μC表示)的超越概率(用Pf表示),Pf表達式為:

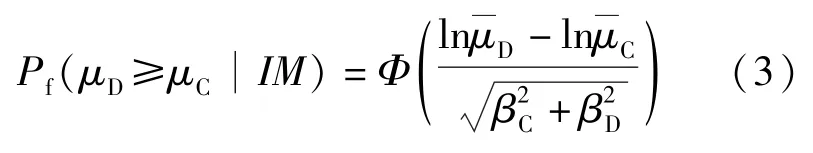
式中:μD和μC一般服從對數正態分布[7];Φ(g)為正態分布函數;為結構地震需求參數;μD為結構抗震能力參數均值;βC、βD為對數標準差。

2.2 結構抗震能力參數μc

現行《建筑抗震設計規范》(GB50011 -2010)將建筑結構遭遇各種水準的地震影響時,其可能的損壞狀況和繼續使用的可能性,明確劃分成五個地震破壞分級: 基本完好、輕微破壞、中等破壞、嚴重破壞和倒塌[8]。易損性分析時,整體結構的各破壞狀態與其最大層間位移角θmax的關系如表3 所示。其中分別為彈性和彈塑性層間位移角限值,對于鋼框架結構,分別取1/250、1/50。

表3 結構不同破壞狀態判別準則和框架結構能力限值Tab.3 Criteria for distinguishing different failure states of structures and capacity limits of frame structures

2.3 結構地震需求參數μD

IDA(增量動力分析)方法中基于對地震的隨機性的考慮,合理選用結構所在場地的足夠多條地震動,通過對每條地震動記錄不斷調幅,形成一組不同強度的地震動記錄,在這組地震動作用下對結構進行一系列的非線性動力分析。通過非線性動力分析可得到IDA 曲線,它能夠正確反映地震作用下結構的地震響應需求,即地震需求曲線。

3 工程實例

基于上述地震易損性分析方法,本文對一工程實例進行了地震易損性分析,以此來探究填充墻對鋼框架結構地震易損性的影響。

3.1 工程概況

北京市大興區的一棟鋼框架結構民用建筑,共6 層,首層為食堂,2 ～6 層為員工宿舍。首層高4200mm,2 ～6 層高3200mm,平面布置如圖5 所示。

圖5 結構平面布置(單位： mm)Fig.5 Plane layout of structure (unit: mm)

填充墻均為混凝土空心砌塊,砌塊強度等級為MU10,砂漿強度為Mb7.5,砌體容重為11.8kN/m3,墻厚取190mm。計算得首層填充墻線荷載為9.4 kN/m,2 ～5 層填充墻線荷載為7.29kN/m。壓型鋼板型號YX -120 -230 -690(II)。建筑場地類別為Ⅱ類,抗震設防烈度8度,設計地震基本加速度值為0.20g,設計地震分組為一組,框架抗震等級為二級。基本風壓W0=0.45kN/m2,地面粗糙度為B 類。鋼材采用Q345B。

該結構應用YJK 軟件按照《建筑結構抗震設計規范》[8]和《鋼結構設計規范》[9]條文為控制進行結構設計,充分考慮填充墻對側向剛度的影響,周期折減系數為0.65,填充墻以線荷載形式作用于梁上。設計中對中梁及邊梁剛度予以放大,根據規范分別取放大系數為1.5、1.2。通過計算,結構滿足多遇地震作用下彈性層間位移角1/250 和罕遇地震作用下彈塑性層間位移角1/50的變形控制條件,符合二級框架抗震等級強柱弱梁、強剪弱彎、節點域和長細比、寬厚比等抗震措施要求,結構設計合理。

3.2 鋼框架有限元模型

以該鋼框架結構為基礎,樓板以荷載的形式等效施加于框架梁上,利用ETABS 建立有、無填充墻結構的有限元模型,通過離散的塑性鉸來考慮結構構件的非線性行為。對于鋼結構,需要考慮梁、柱的彎曲變形和剪切變形。其中,梁單元采用主方向的M3 鉸,柱單元采用P-M2 -M3鉸。

填充墻墻厚為190mm,根據式(1)、式(2)計算填充墻等效斜撐模型尺寸,具體參數如表4所示。

表4 等效斜撐具體參數(單位： mm)Tab.4 Specific parameters of equivalent brace (unit: mm)

在等效斜撐中部布設Axial P 塑性鉸,鉸屬性根據上文砌體結構應力-應變關系中四個特征點定義; 實際工程中框架結構與填充墻并不是一個連續體,之間存在間隙,在側向力作用下,兩者邊界會有脫離現象,故用鉸接模擬兩者的連接與實際受力比較符合。在ETABS 中通過釋放斜撐兩端彎矩達到鉸接目的。

圖6 有限元模型Fig.6 Element models

對于無墻結構,填充墻以周期折減的形式考慮,在此基礎上分別對有、無填充墻結構進行模態分析,得到空間結構前三階自振周期如表5 所示。通過對比自振周期可見,有、無填充墻結構前三階自振周期較為接近,表明有限元建模合理。

表5 結構模態自振周期對比Tab.5 Comparison of modal natural vibration periods of structures

4 鋼框架結構地震易損性分析

從PEEK 強震數據庫中挑選與我國II 類場地類似,且滿足ATC - 63[10]所要求的震級超過6.5、PGA超過200gal 的13 條強震地震記錄,其信息見表6。各地震波的加速度反應譜及規范設計反應譜見圖7。

表6 地震動記錄Tab.6 Earthquake Records

圖7 各地震記錄加速度反應譜及設計反應譜Fig.7 Acceleration response spectra and design response spectra of seismic records

4.1 各地震記錄下IDA曲線

采用ETABS 直接積分法對兩模型選取的地震動樣本逐一進行IDA分析,獲得PGA與最大層間位移角θmax的關系,繪制IDA 曲線,如圖7 所示。

如圖8 所示,因地震波具有隨機性特點,在同一PGA 下,不同地震記錄得出的結構的地震響應,即最大層間位移角θmax有明顯差異。但從IDA 曲線簇大致形狀可以看出,純框架結構IDA曲線更無序、更雜亂,離散性更大。這表明填充墻提高了結構在地震作用下的穩定性。為進一步對結構地震響應平均水平進行表征,對IDA 曲線簇進行統計分析。

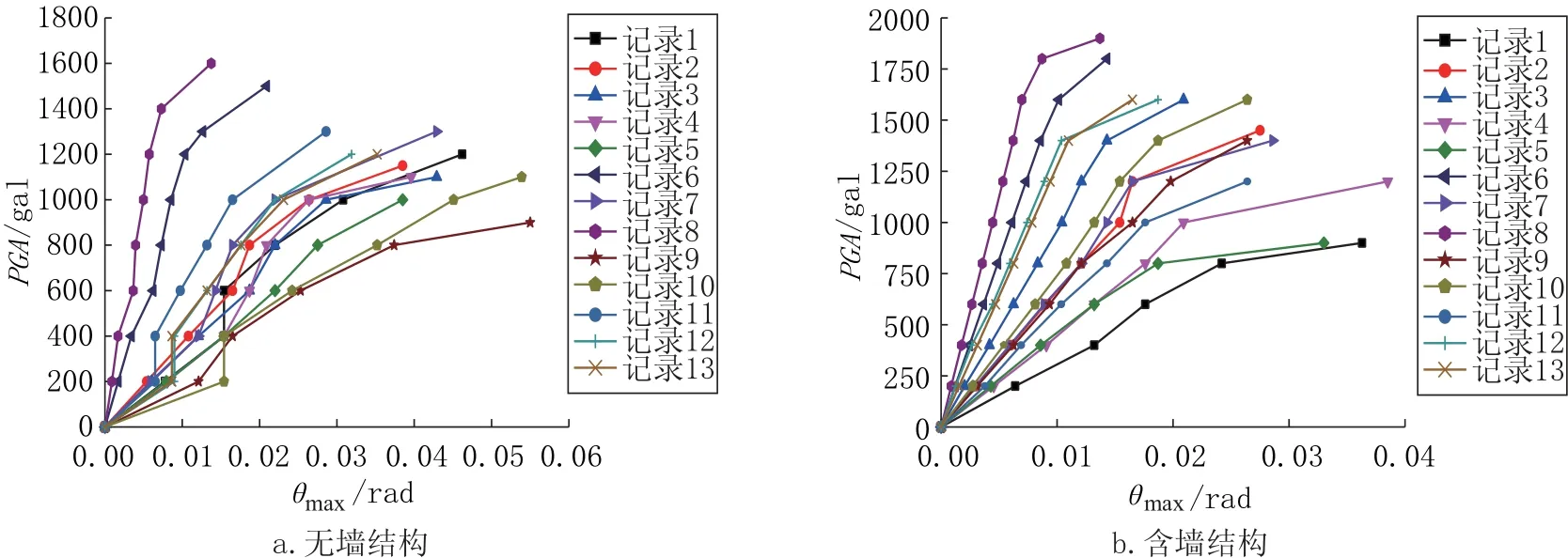
圖8 結構IDA 曲線Fig.8 Structural IDA curve

研究表明,50%概率分位曲線能反映結構平均響應水平[11],常用其作為結構抗震性能評價的依據。此外,為了衡量各控制參數的變異性,即不同地震動形成的IDA 曲線的離散程度,可以根據具體需要,得到正負一倍標準差的16%、84%概率分位IDA 曲線,如圖9 所示。用這三條分位數曲線來表征全部IDA 曲線的平均水平和離散性。

由圖9 可以看出在相同PGA下,含填充墻結構的最大層間位移角小于無墻結構,這表明填充墻有效提高了結構的側向剛度。同時通過對比50%分位線可以發現,純框架結構在最大層間位移角達到2.5%時,結構達到極限狀態。而含填充墻結構在層間位移角達到2.0% 時,結構達到極限狀態。二者所對應的極限PGA值分別為1100gal、1300gal,可見填充墻使結構的極限承載力提高約18.2%,并降低了結構的延性。

4.2 鋼框架結構地震易損性曲線

將兩模型的50%概率分位線作為結構地震需求曲線,結合表3 將結構五種狀態下最大層間位移角限值代入公式(3),獲得兩結構在不同性態條件下的易損性曲線。其中當IM以地震加速度PGA為自變量時,取0.5[12]。

為方便統計,定義BI、SD、MD、CD、ED分別對應于基本完好、輕微破壞、中等破壞、嚴重破壞、倒塌五種狀態,B、I 分別對應于純框架結構、含填充墻結構。由圖10 在可知,四種破壞狀態下,含填充墻結構的超越概率均明顯低于純框架結構。其中PGA為200gal 時,純框架結構輕微破壞、中度破壞、嚴重破壞、倒塌四種狀態下的超越概率分別為60.87%、22.49%、2.26%、0.16%,含填充墻結構為 32.4%、6.83%、0.31%、0.01%; 400gal 時純框架結構分別為94.82%、72.43%、25.73、5.57%,含填充墻結構分別為82.5%、46.1%、8.9%、1.1%。同理根據圖10 也可知在PGA為其他值時結構四種破壞狀態的超越概率。通過對比分析可知,填充墻使結構四種狀態的超越概率明顯降低,提高了結構在地震作用下的安全性,使結構能夠抵抗更強的地震作用。

圖9 分位IDA 曲線Fig.9 Bit IDA curve

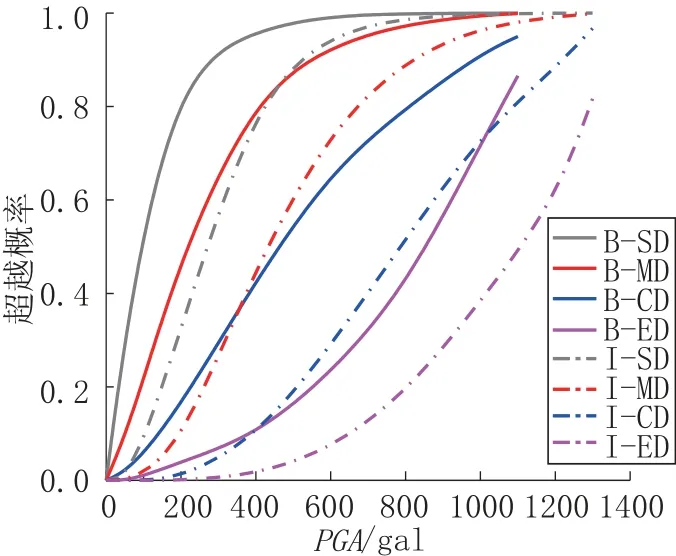
圖10 超越概率對比Fig.10 Transcendental probability comparison chart

4.3 鋼框架結構風險性分析

通過易損性曲線,可以得出結構在某地震強度作用下不同破壞狀態發生的概率,從而為地震災害的損失評估和風險預測提供一定的參考。

由圖11 可知,有、無填充墻結構五種狀態下PGA跨越范圍,如表7 所示。

圖11 結構各破壞狀態的概率曲線Fig.11 Probability curves of failure states of structures

表7 結構不同各狀態下PGA 范圍Tab.7 The range of PGA in different states with different structures

由圖11、表7 可知,當純框架結構處于輕微破壞PGA范圍時,含墻結構處于基本完好。當純框架處于中等破壞PGA范圍時,含墻結構處于輕微破壞,可見填充墻可有效降低主體結構破壞程度。同時通過對比有無填充墻結構發現,純框架結構在PGA＜768gal 范圍內,即純框架結構不致倒塌范圍內,純框架結構嚴重破壞狀態的概率最高,而含墻結構在此區間內中等破壞狀態概率最高,這也說明了填充墻有效地減輕了結構破壞程度,增加了結構安全性; 隨著地震幅值的增加,結構受破壞程度越來越嚴重,就結構破壞狀態而言,純框架結構處于嚴重破壞狀態跨越的PGA范圍最廣,而在加填充墻后結構處于中等破壞狀態跨越的PGA范圍最廣。

4.4 破壞概率矩陣

我國規范8 度(0.2gal)設防區對小震、中震、大震的PGA的定義分別為70gal、200gal、400gal。結合圖10,形成結構破壞概率矩陣如表8 所示。由表8 可知,填充墻提高了結構基本完好的概率,降低了各破壞狀態的發生概率,有效地改善了結構的抗震性能。

圖12 可以更直觀地對比大震、中震及小震下不同破壞狀態的概率,可以發現: 在小震下填充墻對基本完好、輕微破壞及中等破壞概率影響較明顯,且二者基本完好概率最高; 在中震下填充墻對基本完好、輕微破壞、中等破壞、嚴重破壞四中狀態影響均比較顯著,中震下無墻結構輕微破壞概率最高,含墻結構基本完好概率最高; 在大震下填充墻對五種狀態影響均比較顯著,此時無墻結構中等破壞概率最高,而含墻結構輕微破壞概率最高。同時也可發現隨著地震動的加強,填充墻的影響作用愈顯著。尤其在大震下,填充墻有效地降低了結構嚴重破壞及倒塌概率,嚴重破壞概率由33.31%降低為7.8%,倒塌概率由8.14%降低為1.1%,根據ATC -63[9]報告建議: “設防大震下倒塌概率小于10%即認為達到大震性能的要求,可見設計滿足大震性能要求,同時填充墻能有效提高結構抗倒塌能力。

表8 結構破壞概率矩陣Tab.8 Structural failure probability matrix

圖12 各設防地震下破壞概率對比Fig.12 Comparisons of failure probability under different fortified earthquakes

5 結論

本文按我國抗震規范設計了鋼框架結構,并利用ETABS 建立含填充墻及無墻空間有限元模型,對兩種結構模型分別進行了地震易損性分析和風險性分析,并定量對兩結構進行評估。以此探究在地震作用下填充墻對結構抗震性能的影響,以期對鋼框架結構抗震設計提供一定參考。結論如下:

1.結合我國規范定義的五個性態點對結構進行了易損性分析,使地震易損性分析與我國現行規范有效銜接,便于對結構進行風險性評估。

2.通過對比有填充墻結構50%分位線及結構易損性曲線,表明填充墻的存在提高了結構的抗側剛度、極限承載力,減少了結構側向位移,降低結構延度。

3.通過結構破壞概率曲線及破壞概率矩陣發現,在小震下填充墻對于結構抵抗破壞能力的影響作用并不明顯,隨著地震作用增強,這一影響逐漸加強,表明填充墻可有效改善結構抗震性能。

4.按照我國規范設計的結構能滿足大震性能設計倒塌概率小于10%的要求,對比發現加填充墻后結構倒塌概率由8.14%降低為1.1%,表明填充墻能有效降低結構倒塌概率。