懸索橋鋼桁梁加勁梁局部受力及屈曲特性有限元分析

桂睿 趙興宏 肖永銘

(1.中國公路工程咨詢集團有限公司 北京100089;2.北京市市政工程設計研究總院有限公司 100082)

引言

目前,懸索橋加勁梁形式主要有鋼箱梁及鋼桁梁兩種形式[1,2],在跨海或跨越寬闊河面等運輸條件較好的情況下主要采用鋼箱梁,在高山峽谷地區中,由于運輸條件差、加工場地修建成本較高,大多采用鋼桁梁加勁梁[3]。與鋼箱梁相比,鋼桁梁加勁梁設計時需對每根桿件單獨進行受力分析及屈曲分析。規范中通過考慮穩定屈曲系數對桿件承載力進行折減。但對于鋼桁梁而言,桿件兩端邊界條件極為復雜,桿件計算長度難以確定。在實際工程中,桿件在節點處通過節點板進行連接,節點處桿件約束條件既不是鉸接,也不是理想剛接。以往研究中大多采用桿單元對桁架進行分析,節點處的剛度無法準確模擬。

本文采用板殼單元建立三維模型,對節點連接處進行精細化模擬,并對鋼桁梁結構進行屈曲分析,驗算桿件應力并對規范建議桿件計算長度進行修正。分析結論可為今后同類工程設計提供參考。

1 工程概況

本文以某鋼桁梁懸索橋為背景,大橋主跨800m,主纜矢跨比1:10,主纜中心間距28m,吊索標準間距12m。主橋加勁梁采用單跨鋼桁梁,由主桁架、主橫桁架、上下平聯組成。主桁架為帶豎桿的三角形腹桿式結構,由上弦桿、下弦桿、豎腹桿和斜腹桿組成。上弦桿、下弦桿采用箱形截面,豎腹桿采用箱型斷面,在節點板處由箱型斷面轉化為H 型截面。主桁架高7.0m,桁寬28m,標準節間長度6m。一個標準節段長度12m,由2 個節間組成,在每節間處設置一道主橫桁架。主橫桁架采用單層桁架結構,由上、下橫梁及豎、斜腹桿組成,其中上下橫梁采用箱形截面,腹桿均采用箱型截面。上、下平聯均采用K 形體系、箱型截面。

2 有限元建模

本文利用三維有限元軟件建立加勁梁節段空間模型,加勁梁節段模型的邊界條件取自整體計算MIDAS CIVIL 模型,整體模型示意見圖1。考慮了結構軸力幾何剛度變化和結構大位移的影響,計算模式采用全橋空間模型,其中塔、梁均采用三維梁單元來進行模擬,纜索和吊桿作為無抗彎剛度的索單元來處理。

圖1 整體模型示意Fig.1 Sketch map of overall model

局部分析模型約束條件及荷載與整體模型基本一致,端部邊界條件剛度精確計算較困難,因此邊界約束采用固定約束+6 自由度強迫位移模擬。強迫位移取自整體模型計算結果,加勁梁吊桿約束采用集中力進行模擬。邊界條件中節點強迫位移,按照總體計算結果中主桁應力最大時對應內力選取。

加勁梁節段模型中,桁架桿件及橋面系工字鋼采用板單元,節點處采用板殼進行精細化模擬,混凝土橋面板采用實體單元,標準段計算模型縱向長度取48m,共4 個標準節段。節段模型見圖2。

圖2 節段模型示意Fig.2 Sketch map of segment model

3 局部受力特性分析

通過有限元計算分析,對懸索橋鋼桁架加勁梁在靜力荷載組合工況下的變形特性和破壞形態進行研究,從而找到鋼桁架加勁梁薄弱區域,同時對應力分布規律進行研究,分析鋼桁架加勁梁的工作性能及破壞機理。

3.1 局部分析與整體分析對比

上弦桿內力最大工況下,整體模型與局部模型各桿件應力對比見表1,表中應力均為桿件中部應力,忽略局部模型中應力集中影響。

表1 整體模型與局部模型應力對比Tab.1 Stress comparison between global model and local model

整體模型與局部模型計算結果基本一致,說明局部模型中加載方式可行,邊界條符合要求。

3.2 上弦桿與上橫梁節點

上弦桿與上橫梁節點應力如圖3 所示,上弦桿與上橫梁節點受力復雜,節點板與懸索橋纜索系統吊桿相連,最大mises 應力為259MPa,最大應力位于節點板圓弧倒角處,在疲勞應力作用下,該處存在撕裂風險,設計時應采取增加圓弧倒角半徑或采取局部加強措施。

3.3 下弦桿與下橫梁節點

有限元計算結論與懸索橋整體計算桿單元模型中桿件應力分布基本一致,下弦桿與下橫梁節點處應力見圖4 所示,最大應力為210MPa,最大應力位于下弦桿。

3.4 橫梁節點

上平聯桿標準段采用箱型截面,與節點板相連處兩側箱型截面腹板合并,截面變化為工字型截面。節點處應力見圖5 所示,應力云圖表明,工字型截面與節點板連接處存在截面突變,工字型截面腹板端部存在應力集中現象,設計時應采取構造措施對工字型腹板進行剛度削弱,使連接處腹板存在漸變段,削弱突變導致的應力集中現象。

橫梁斜腹桿與橫梁連接節點處,斜腹桿截面同樣由箱型轉化為工字型,截面變化處腹板存在彎折現象,導致腹板存在平面外受力,彎折處局部應力過大。設計時應在彎折處桿件內設置橫隔板,減小腹板平面外受力。

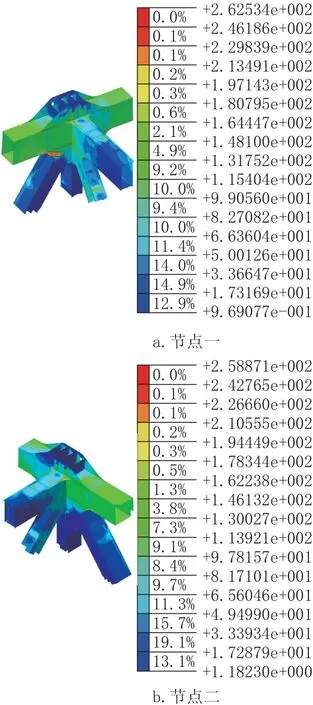
圖3 上弦桿與上橫梁節點應力(單位： N/mm2)Fig.3 Nodal stress of upper chord and upper beam(unit: N/mm2)

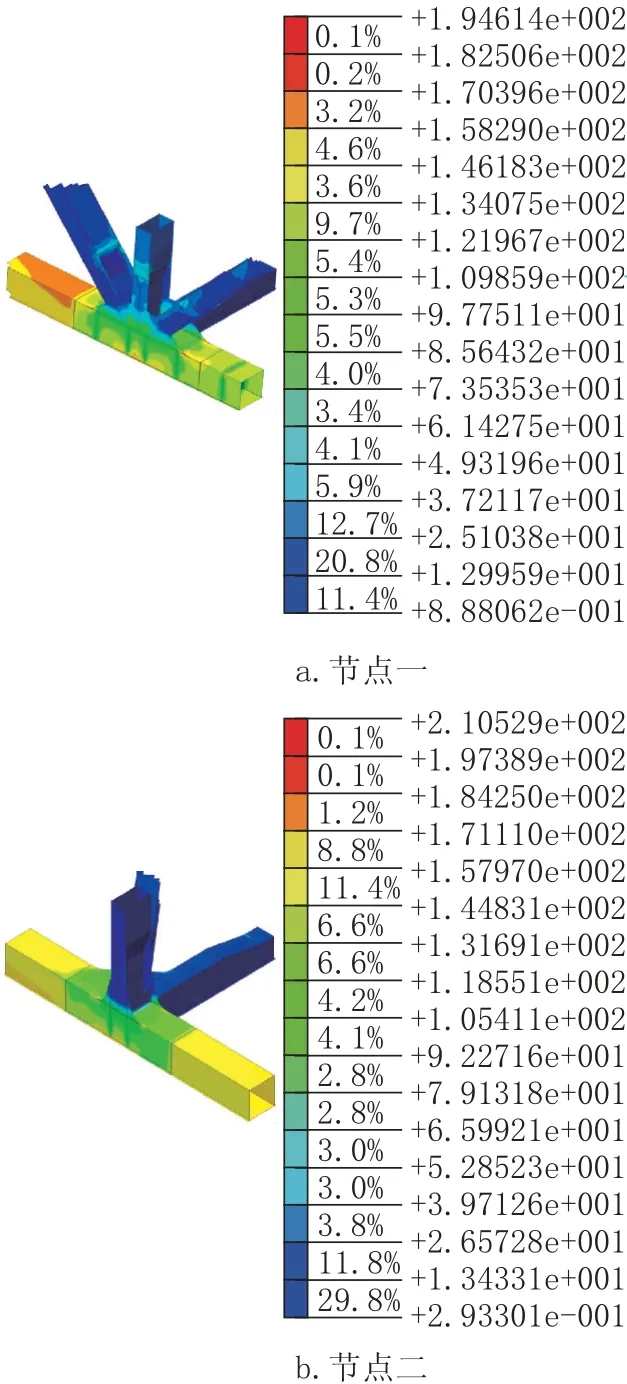
圖4 下弦桿與下橫梁節點應力(單位： N/mm2)Fig.4 Nodal stress of lower chord and lower beam(unit: N/mm2)

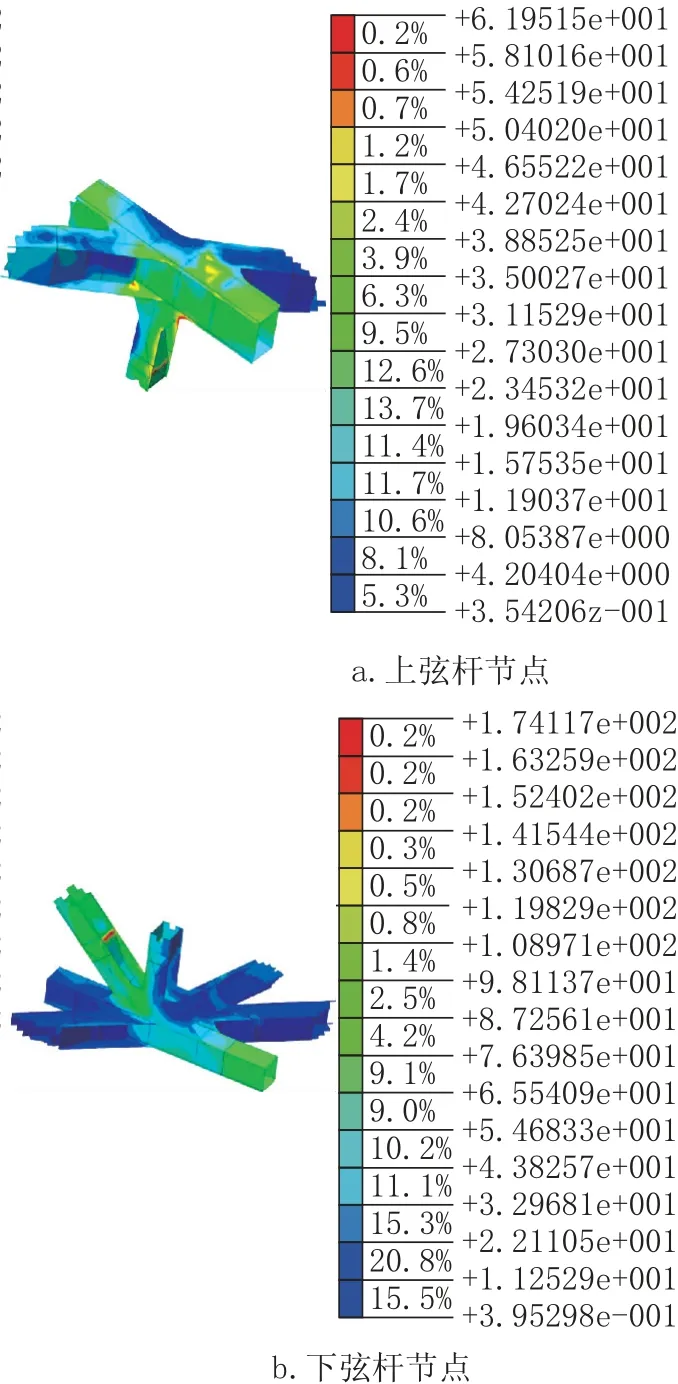
圖5 橫梁節點應力(單位： N/mm2)Fig.5 Nodal stress of beam(unit: N/mm2)

4 屈曲分析

分別對梁段整體和單根桿件屈曲進行計算分析。屈曲分析邊界條件取自全橋整體計算模型,梁端節點采用固定約束,節點施加6 自由度強迫位移,強迫位移數值取自標準組合工況下該梁段節點位移,梁段荷載按標準組合考慮。

4.1 整體屈曲分析

雖然特征值屈曲未考慮非線性及初始缺陷,只適用于理想構件,但該方法計算成本較低,且為非線性屈曲分析的基礎,可揭露非線性屈曲計算結果上限,因此目前仍被廣泛采用。本文采用板殼單元建立模型,單元數量較多,為節約計算成本,采用特征值屈曲進行分析[4,5]。

整體屈曲分析采用荷載標準組合,因邊界條件采用固定約束加強迫位移模擬,邊界強迫位移、恒載及可變荷載均設置為變量,同比例變化,保證強迫位移邊界條件與荷載相匹配。

經過特征值屈曲分析,得出桁架標準節段一階屈曲系數為10.03,表明桁架整體穩定性較好。桁架標準節段一階屈曲模態如圖6 所示,一階屈曲模態表現為主桁架上弦桿出現屈曲,屈曲位置位于兩吊桿中間部位。

圖6 加勁梁一階屈曲(屈曲系數10.03)Fig.6 First order buckling of stiffening beams (buckling coefficient 10.03)

4.2 單根桿件屈曲分析

鋼桁架桿件邊界條件十分復雜,規范經驗值無法準確定義桿件計算長度。根據《鋼結構設計規范》(GB 50017 -2003)[6],鋼桁架弦桿計算長度為桁架側向支承點之間的距離,但對于鋼桁架加勁梁,主梁全長800m,僅吊桿及兩端支座對加勁梁有支承作用,加勁梁無側向支承,根據規范確定弦桿計算長度較困難,實際設計時一般采用節點中心間距。常規計算一般已知計算長度,通過歐拉公式計算歐拉應力,本文通過有限元分析求得桿件屈曲臨界應力,并通過歐拉公式反向推算計算長度及長細比,從而對規范計算長度進行驗證[7,8]。

為準確模擬桿件邊界條件,計算模型仍采用4 節段模型,全長48m,邊界采取固定約束,對應各桿件分別建立荷載工況,各荷載工況僅對需計算的單根桿件兩端施加單位軸向荷載,對每根桿件逐個進行屈曲分析。考慮中部節段桿件邊界條件較準確,屈曲分析選取中部節段桿件。上弦桿及豎腹桿屈曲如圖7 所示。

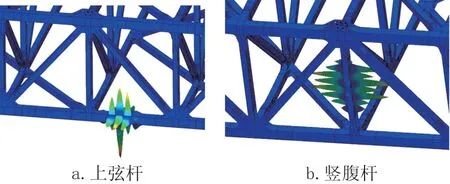
圖7 上弦桿及豎腹桿屈曲Fig.7 Buckling of upper chord and vertical web members

通過有限元軟件求得單根桿件在單位荷載下的屈曲系數及單位荷載下桿件截面應力,二者乘積即為桿件歐拉應力,根據《公路鋼結構橋梁設計規范》(JTG D64 -2015)A.0.3,桿件長細比可按下式近似計算:

由以上公式及有限元法求得桿件長細比及計算長度見表2。

表2 長細比及計算長度匯總Tab.2 Slenderness ratio and computation length summary

根據表2 計算長度及《鋼結構設計規范》(GB 50017 -2003)附錄C 選取各桿件穩定系數。上弦桿及下弦桿桿件兩端節點間距為6m。以往工程中,節點一般按鉸接計算,平動自由度為剛性約束,放松轉動自由度,桿件計算長度取節點中心距離6m,桿件穩定折減系數計算為0.943。但桁架節點平動實際應為彈性約束,平動約束剛度由桁架整體剛度決定,而懸索橋中桁架整體剛度相對較小,弦桿平動位移不可忽略,彈性約束剛度按剛性考慮誤差較大。由有限元計算結果,上弦桿及下弦桿桿件計算長度為8.2m。桿件折減系數為0.895,壓桿容許應力為264MPa。

根據規范建議值,橫梁及腹桿計算長度均為節點間距,即桿件兩端均按鉸接考慮,未考慮節點轉動約束,桿件計算長度相對保守。本文將有限元計算得到的屈曲應力代入歐拉公式,計算得出桿件計算長度約為0.7 倍節點間距。計算結果表明橫梁及腹桿桿件剛度相對于節點約束剛度較小,桿件可按兩端剛性連接進行計算。

5 結論

通過對鋼桁架加勁梁建立三維有限元模型,并對桿件連接節點進行精細化處理分析,研究了桁架局部受力特性。同時研究了桁架體系屈曲特性及桿件計算長度,并與規范計算方法對比,得出以下結論:

1.懸索橋鋼桁架節點板在設計時不僅應考慮撕裂等常規計算,尚應考慮應力集中產生的局部應力過大現象,采取構造措施以減小應力集中的影響。

2.桿件截面存在變化時,應設置過渡段,使截面剛度及應力狀態均勻變化,同時在變化處平面板件易產生平面外受力現象,設計時應采用構造措施以減小板件平面外受力。

3.通過對鋼桁架桿件進行屈曲分析,使用有限元方法及歐拉公式推導出桿件計算長度,并與規范值進行對比,發現采用有限元法計算桿件更為精確,對于加勁梁主弦桿,規范公式計算折減系數較小,計算結果安全儲備度略小; 對于其余桿件剛度相對于加勁梁整體剛度較小,按規范公式計算較保守,可根據具體情況進行調整。