分析全球副高指數與蘇北地區降水關系
周 威 曹春泉 王 巖
(江蘇省淮沭新河管理處,江蘇 淮安 223001)
1 研究的目的和背景
我國的降水在蘇北和蘇南地區也存在一定的差異,長系列徑流實測資料更有利于準確地探尋隨機水文現象統計規律。本文選取1961年到1997年的4月和5月的平均降水資料,分析了蘇北地區的降水及其規律的變化,通過數據處理分析和建立相關的水文預報模型確定蘇北地區的降水分布特征及其降水規律。
2 蘇北地區降水概況
蘇北地區一般4、5月份進入雨季,一直到9、10月份。蘇北地區多年平均降雨量達到800~1 000 mm,其中在汛期占比偏大,但是蘇北地區數量庫容有限,上游來水也是豐枯不均,總的來說,蘇北地區水資源相對比較緊缺。
3 計算步驟
3.1 建立標準化的正規方程組
假設預報因子X是由m個組成,每個因子的長度為n;預報對象y,其長度為n。在逐步回歸中采用的是國土調查逐漸標準化的正規回歸方程組:

根據上述方法所得到的正規方程組:
回歸系數bi是相應的預報因子的系數,但各個因子的單位不一樣,為消除單位的影響,引入標準回歸系數的概念。對式進行變換。
令:
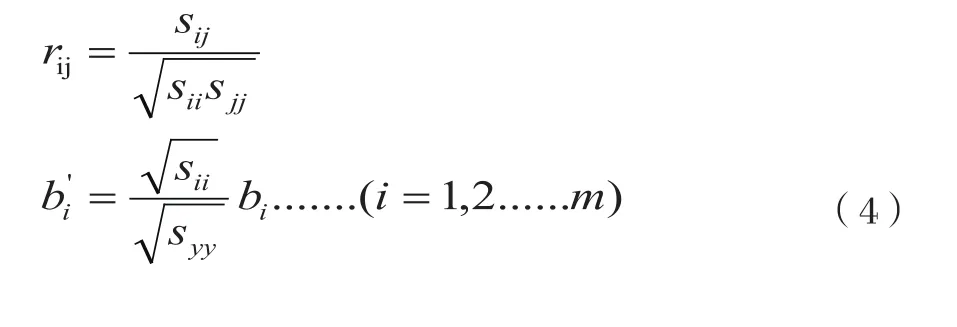
有如下關于bi’的相關矩陣方程組:
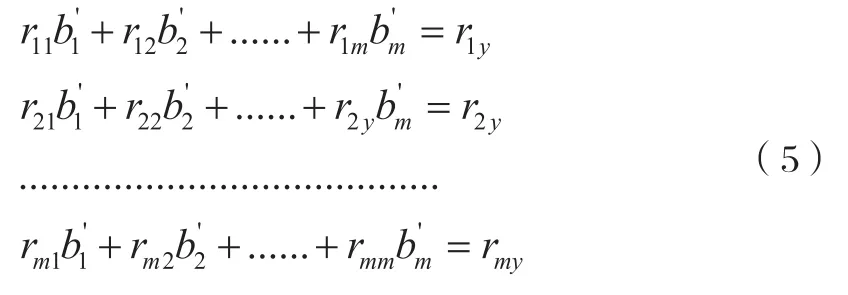
方程組關于標準化回歸系數的標準化正規方程組,其中的回歸系數bi’與x及y所取的單位無關。稱為標準回歸系數。
相應的增廣矩陣:

3.2 引入或剔除變量的F檢驗
(1) 定義方差比 :

給定自由度 (1,n-p-1),信度α查表得Fα,若Fi>Fα拒絕原假設,xi作用顯著,可以引進xi。
若Fi≤Fα接受原假設,xi作用不顯著,要剔除xi。
(2) 剔除因子 :

當F2i≤Fα時,剔除因子。
(3) 引入因子 :
引進因子公式:
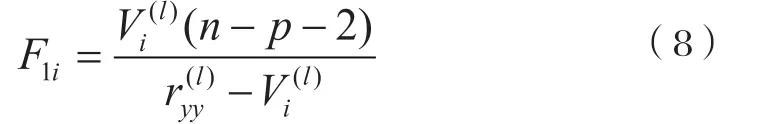
給定信度α,自由度 (n-p-2) 查表得Fα值,當F1i>Fα時引進因子。
(4) 標準回歸方程:

(5) 回歸方程 :
代入關系式:
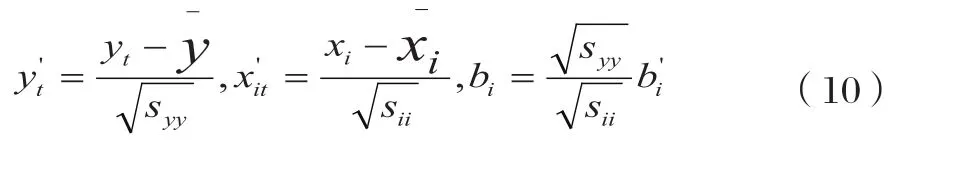
得回歸方程:

4 回歸效果的檢驗
利用逐步回歸分析所得到的優勢因子計算其復相關系數和剩余標準差sy,對回歸方程回歸效果進行檢驗。
(1) 復相關系數 :

R成為復相關系數,由它來衡量回歸效果的好壞,0≤R≤1,復相關系數R>Rα,則回歸效果就好。
(2) 剩余標準差 :

剩余標準差sy可作為衡量回歸效果和預報精度的標志。若sy愈小,則回歸方程來預報y的值就愈精確。
5 結果分析
根據已有的降雨資料和降雨資料數據處理分析及其變化規律,并且從中挑選出相關性大的影響因子然后利用編寫好的程序得出預報方程的系數,建立預報模型并根據此模型對1961~1997年的蘇北地區4月份和5月份平均降雨量進行預報。
5.1 建立預報模型
首先使用單相關系數計算方法,從83項大氣環流因子中挑選出部分與預報對象相關性較高的因子,在本節中預報因子是提前1年來挑選的( 即預報對象的序列為1953~2008年,預報因子序列為1952~2007年),挑選因子的顯著性水平信度a為0.01時通過單相關系數檢驗可以初選出15個大氣環流因子,而信度a為0.05時通過但相關系數檢驗可以初步選出33個大氣環流因子。
5.2 實驗結論分析
本次研究的是全球副高指數與蘇北地區降水的關系分析,通過本次課設對相關數據的實測值處理分析得到了該地區4月份和5月份的平均降水,然后通過多元回歸分析、逐步回歸分析和M-K突變檢驗的方法處理分析,通過相關模型得出一些相應的結論:首先,通過在因子表中篩選出3組因子,通過相關系數法和給定的逐步回歸和多元回歸輔助程序得到相關趨勢圖。通過單相關系數法和逐步回歸給定的程序,得到擬合期的誤差范圍是0.142 873 061,實驗期的誤差范圍是0.080 938 452,屬于允許誤差范圍,符合標準。
6 結語
本次主要是進行數據的處理與計算,通過逐步回歸的方法去分析和處理數據,最后得出擬和曲線圖,探究全球副高指數與蘇北地區降水的關系。

